NVIDIA_EDM论文解读

本文主要介绍Nvida发表的关于score-based的文章 Elucidating the Design Space of Diffusion-Based Generative Models，该文从采样方法，训练方法和数据预处理三个维度对score-based模型进行了优化。

• 1. 扩散过程的一般性表达
• 2. 确定性采样的改进
  • 1.1 要点概述
  • 1.2 深度解读
    • 1.2.1 Score matching
    • 1.2.2 Langevin dynamics
    • 1.2.3 流形假设带来的挑战
    • 1.2.4 低密度数据区域带来的挑战
    • 1.2.5 Noise Conditional Score Networks
    • 1.2.6 Annealed Langevin dynamics
  • 1.3 相关结论
    • 1.3.1 可视化效果
    • 1.3.2 定量分析
    • 1.3.3 原文结论
• 2. Improved Techniques for Training Score-Based Generative Models
  • 2.1 要点概述
  • 2.2 深度解读
    • 2.2.1 基础 score-based 模型的不足
    • 2.2.2 如何设计每一层的加噪强度
      • 2.2.2.1 设置初始噪声强度 $\sigma_1$
      • 2.2.2.2 设置中间层的加噪强度
    • 2.2.3 如何注入噪声条件信号
    • 2.2.4 配置退火朗之万动力学采样
    • 2.2.5 滑动平均提高稳定性
    • 2.2.6 NCSNv2
  • 2.3 相关结论
    • 2.3.1 定量分析
    • 2.3.2 原文结论
• 3. SCORE-SDE
  • 3.1 要点概述
  • 3.2 深度解读
    • 3.2.1 模型回顾
      • 3.2.1.1 DENOISING SCORE MATCHING WITH LANGEVIN DYNAMICS (SMLD)
      • 3.2.1.2 DENOISING DIFFUSION PROBABILISTIC MODELS (DDPM)
    • 3.2.2 SDEs 框架下的 score-based 生成模型
      • 3.2.2.1 利用 SDEs 对数据进行扰动
      • 3.2.2.2 利用 reverse SDEs 对数据进行采样
      • 3.2.2.3 估计 SDE 中的 score
      • 3.2.2.4 VE和VP SDEs
    • 3.2.3 reverse-time SDEs 框架下的采样器
      • 3.2.3.1 predictor-corrector 采样框架
    • 3.2.4 PROBABILITY FLOW
    • 3.2.5 不同采样器的性能对比
    • 3.2.6 网络结构的提升
  • 3.3 相关结论
    • 3.3.1 定量分析
    • 3.3.2 原文结论
• 4. Consistency Models
  • 4.1 要点概述
  • 4.2 深度解读
    • 4.2.1 从 概率流 ODE（PF ODE） 开始
    • 4.2.2 一致性模型的定义
      • 4.2.2.1 参数化
    • 4.2.3 蒸馏法训练一致性模型
    • 4.2.4 独立训练一致性模型
    • 4.2.5 超参数选择
    • 4.2.6 性能对比
      • 4.2.6.1 蒸馏方法的对比
      • 4.2.6.2 单步生成效果对比
  • 4.3 结论总结

1. 扩散过程的一般性表达

根据[Song]¹的工作，扩散过程可以形式化为一个概率流常微分方程（PF ODE），即：

\[\mathrm{d} \boldsymbol{x}=\left[f(t) \boldsymbol{x}-\frac{1}{2} g(t)^2 \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x})\right] \mathrm{d} t . \tag{1}\]

本文作者对上式进行了重参数化（具体推导过程可以参考附录B.2），得到：

\[\mathrm{d} \boldsymbol{x}= \left[\frac{\dot{s}(t)}{s(t)} \boldsymbol{x}-s(t)^2 \dot{\sigma}(t) \sigma(t) \nabla_{\boldsymbol{x}} \log p\left(\frac{\boldsymbol{x}}{s(t)} ; \sigma(t)\right)\right] \mathrm{d} t . \tag{2}\]

其中 $s(t)$ 表示对输入 $\boldsymbol{x}$ 的缩放，即\(\boldsymbol{x}=s(t) \hat{\boldsymbol{x}}\)。$\hat{\boldsymbol{x}}$ 表示未缩放的版本。

需要注意的是，式（2）中除了score $\nabla_{\boldsymbol{x}} \log p$ 需要通过训练神经网络估计得到外，其他都是预设的超参数。

假设我们已有score函数，那根据式（2）就可以使用一些ODE-Solver生成样本。不同求解器（一阶or二阶），求解节点（离散化方式）决定了最终求解的精度以及所需要的时间复杂度。常见的欧拉法是一阶近似，作者推荐使用二阶Heun近似，并在不同模型上验证了该采样方法的有效性。

根据公式（2），作者概述了当前几种主流生成模型的参数配置。

	VP[Song]1 参考C1.1	VE[Song]1 参考C2.1
ODE solver	Euler	Euler
Timesteps $t_{i<N}$	$1+\frac{i}{N-1}\left(\epsilon_{\mathrm{s}}-1\right)$	$\sigma_{\max }^2\left(\sigma_{\min }^2 / \sigma_{\max }^2\right)^{\frac{i}{N-1}}$
Schedule $\sigma(t)$	$\sqrt{e^{\frac{1}{2} \beta_d t^2+\beta_{\min} t}-1}$	$\sqrt{t}$
Scaling $s(t)$	$1 / \sqrt{e^{\frac{1}{2} \beta_{\mathrm{d}} t^2+\beta_{\min } t}}$	$1$

2. 确定性采样的改进

作者认为，在训练阶段所使用的配置——也就是 $\sigma(t)$，$s(t)$ 以及 $\left{t_i\right}$ 不一定沿用到推理阶段，反之亦然。

1.1 要点概述

本文提出了一种新的基于score的生成模型，所谓score可以大概理解成（对数）概率密度关于样本（$\mathbf{x}$） 的导数。换句话说，如果知道了score值，那么也就知道了样本沿着什么方向的演变可以使自身发生的概率变大，而那些概率更大的样本也就是相对正常的样本。而使得训练中的训练样本对应的概率密度最大对应的就是极大似然估计。

作者首先概述了现有的训练生成模型的主流范式，也就是：

• likelihood-based 方法 和 生成对抗网络。前者使用对数似然（或者易处理的代理）作为优化目标，后者使用对抗训练的方案最小化模型预测分布与真实数据分布之间的差异，如 $f$-散度；

同时也总结了两种方案的不足：

• likelihood-based 方法（如自回归模型，归一化流模型）在模型结构和优化目标上存在限制；GAN 的训练存在不稳定的情况，同时GAN模型不适合评估和对比不同模型（无法计算样本的概率值，即$p(\mathbf{x})$）。

总结下来，score-based生成模型训练容易，但推理复杂（成本高）；而GAN训练困难，但推理简单。

基于此，作者提出一种新的数据生成的建模方案 Score-based generative models，主要包括：

• 训练一个神经网络估计 $\mathrm{log}\ p(\mathbf{x})$ 的 (Stein) score，即 $\nabla_{\mathbf{x}} \log p(\mathbf{x})$，该梯度表示 $\mathrm{log}\ p(\mathbf{x})$（即 $p(\mathbf{x})$） 增长最快的方向;
• 训练方案使用 score matching，具体说是 denoising score matching;
• 推理阶段（生成样本）使用 Langevin dynamics 和模型估计的 score 值；
• 训练过程存在2个挑战：
  • 高维数据（如图片）通常分布于某个低维的流型（manifold），这就意味着在高维空间中存在大量的空洞，这些空洞会导致 score matching 的训练失效；
  • 真实分布可能存在一些低密度区域（即样本比较少），在这些区域，score的估计容易失准，进而影响Langevin dynamics 采样，因为在Langevin dynamics采样过程中，通常会先在低密度区域初始化一个样本，然后根据 score值不断更新该样本。如果在低密度区域的score值估计不准，则会影响最终采样得到的样本。
• 为解决上述2个挑战，作者提出：
  • 分层加噪：使用不同强度的高斯噪声对数据进行加噪，一方面加噪声可以缓解维度灾难，另一方面，较强的噪声可以使低密度区域的正常样本周围新增很多辅助样本；
  • 退火朗之万动力学采样：因为在训练过程中使用了分层加噪，所以在推理时，朗之万动力学在不同的加噪层使用不同的噪声强度，该强度由大到小变化（即退火）。

1.2 深度解读

本文主要包含两个重要预备知识：score matching 和 Langevin dynamics，前者用于模型训练，即估计score，后者用于推理，即生成样本。

1.2.1 Score matching

Score matching 是训练 Engery-based Generative Model 的一种方案，用来学习非归一化的统计模型。关于该方法的详细介绍，可以参考MLAPP一书中的24.3节，为降低计算层面的复杂度，score matching 存在某些变种，作者采用了 Denoising score matching。具体而言，对于每一个训练样本 $\mathbf{x}$ ，首先对其进行加噪扰动，扰动核为 \(q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})\)。然后使用优化模型使其预测的score和扰动分布 \(q_\sigma(\tilde{\mathbf{x}}) \triangleq \int q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}) p_{\text {data }}(\mathbf{x}) \mathrm{d} \mathbf{x}\) 的score对齐（即score matching），优化目标被证明与下式等价（注意被匹配的目标从无条件分布score变成了有条件分布score，具体的证明可参考 [Vin11]²）：

\[\frac{1}{2} \mathbb{E}_{q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}) p_{\text {data }}(\mathbf{x})}\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}})-\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})\right\|_2^2\right] \tag{1.1}\]

上式最优解 \(\left.\mathbf{s}_{\boldsymbol{\theta}^*}(\mathbf{x})\right)\) 满足 \(\mathbf{s}_{\boldsymbol{\theta}^*}(\mathbf{x})=\nabla_{\mathbf{x}} \log q_\sigma(\mathbf{x})\)，但只有当所加噪声强度足够小时，我们才有 \(\mathbf{s}_{\boldsymbol{\theta}^*}(\mathbf{x})=\nabla_{\mathbf{x}} \log q_\sigma(\mathbf{x}) \approx \nabla_{\mathbf{x}} \log p_{\text {data }}(\mathbf{x})\)，因为只有在这种情况下 \(q_\sigma(\mathbf{x}) \approx p_{\text {data }}(\mathbf{x})\)。

1.2.2 Langevin dynamics

Langevin dynamics（朗之万动力学）是一种只需要知道概率分布的 score 值 $\nabla_{\mathbf{x}} \log p(\mathbf{x})$ 就可以从分布 $p(\mathbf{x})$ 中生成样本的采样方案。具体而言，给定一个固定步长 $\epsilon>0$ 和一个初始样本 $\tilde{\mathbf{x}}_0 \sim \pi(\mathbf{x})$ （其中 $\pi$ 是一个先验分布），Langevin dynamics 采用迭代生成的方案获得最终的样本：

\[\tilde{\mathbf{x}}_t=\tilde{\mathbf{x}}_{t-1}+\frac{\epsilon}{2} \nabla_{\mathbf{x}} \log p\left(\tilde{\mathbf{x}}_{t-1}\right)+\sqrt{\epsilon} \mathbf{z}_t \tag{1.2}\]

其中 $\mathbf{z}_t \sim \mathcal{N}(0, I)$。当 $\epsilon \rightarrow 0$，$T \rightarrow \infty$，最终的样本 $\tilde{\mathbf{x}}_T$ 将服从真实但未知的分布 $p(\mathbf{x})$。

1.2.3 流形假设带来的挑战

score matching 对于高维数据的训练存在若干挑战，首先，根据流形假设理论，高维空间（即真实样本所处的空间——ambient space）的数据通常被约束在某个未知的低维流形，换句话说，存在某些样本在某些维度方向上没有任何相邻样本（不连续），这使得这些维度的梯度无法定义。

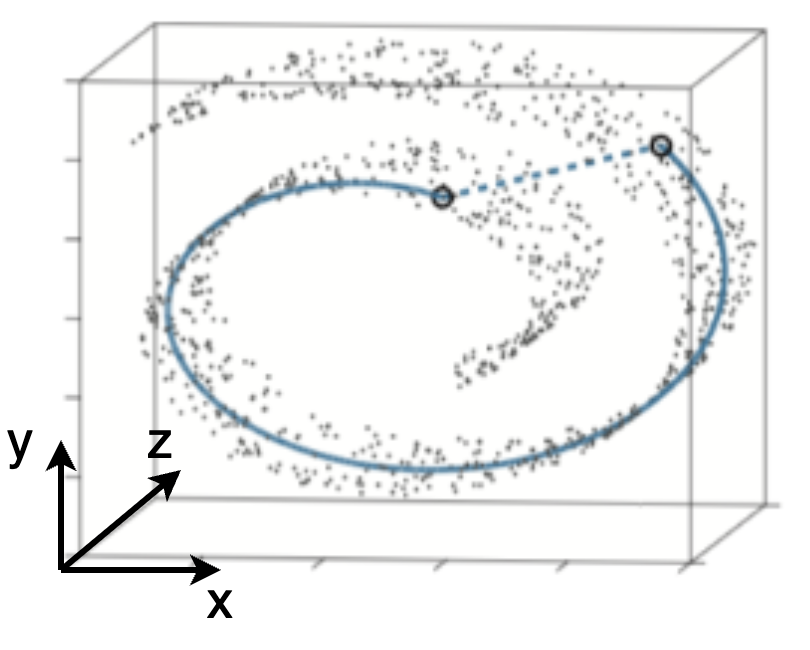
以上图展示的经典的瑞士卷数据为例，我们的数据空间是3维，但真实的数据却分布在一个瑞士卷形状的流形。假设每个点的数值代表所在空间位置的温度 $T(\mathbf{x})$，显然存在很多区域无法定义梯度 $\nabla_{\mathbf{x}}T$ ，此处的 $\mathbf{x}$ 表示3维坐标$(x,y,z)$。

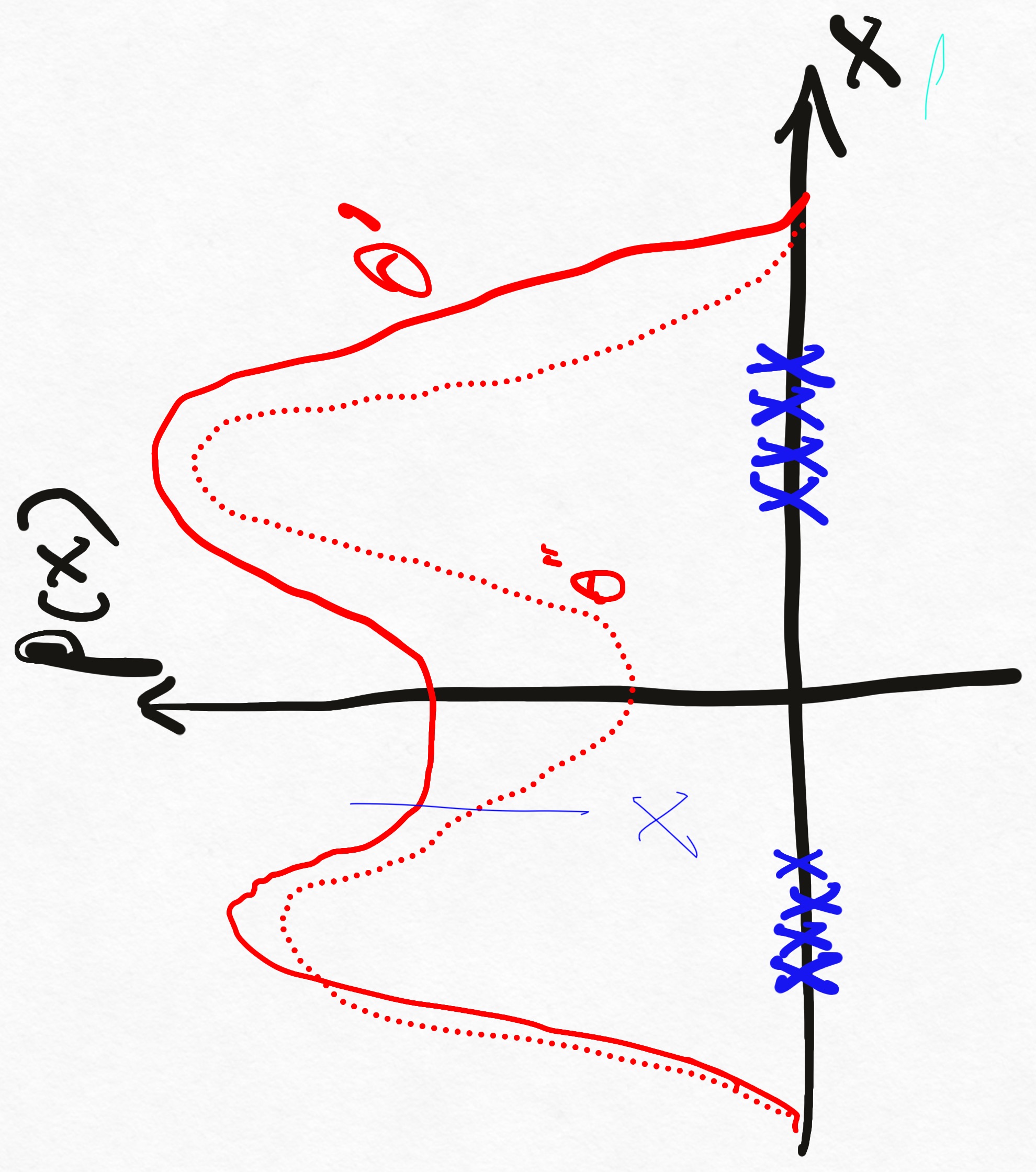
其次，根据 [Hyv¨arinen]³ 中的定理2，只有当概率分布的支撑集为整个空间（数据空间没有空洞），score matching估计的 score 才是一致的，如果数据被约束在某个低维的流形，会导致不一致的 score。如下图所示，如果存在稀疏的区域，那可能存在多个概率模型参数 $\theta^{\prime}$ 或 $\theta^{\prime \prime}$ 满足数据的分布，而此时在 $x$ 处的score则出现不一致，随着数据量的增加， $\theta^{\prime}$ 或 $\theta^{\prime \prime}$ 将趋于一致，相应的每一点的score也具有了一致性。

1.2.4 低密度数据区域带来的挑战

回顾公式（1.1），denoising score matching 需要关于 $p_{\text {data }}(\mathbf{x})$ 求解期望。在实践中，为了估计期望值，首先采样得到样本 \({\mathbf{x}_i}_{i=1}^N \stackrel{\text { i.i.d. }}{\sim} p_{\text {data }}(\mathbf{x})\)，考虑某个低密度区域 \(\mathcal{R} \subset \mathbb{R}^D\)，该区域满足 \(p_{\text {data }}(\mathcal{R}) \approx 0\)。在多数情况下 \({\mathbf{x}_i}_{i=1}^N \cap \mathcal{R}=\varnothing\)，即我们很少采样到那些低密度区域的样本。此时，期望的估计会严重失准，进而导致低密度区域的 score 不再可靠。

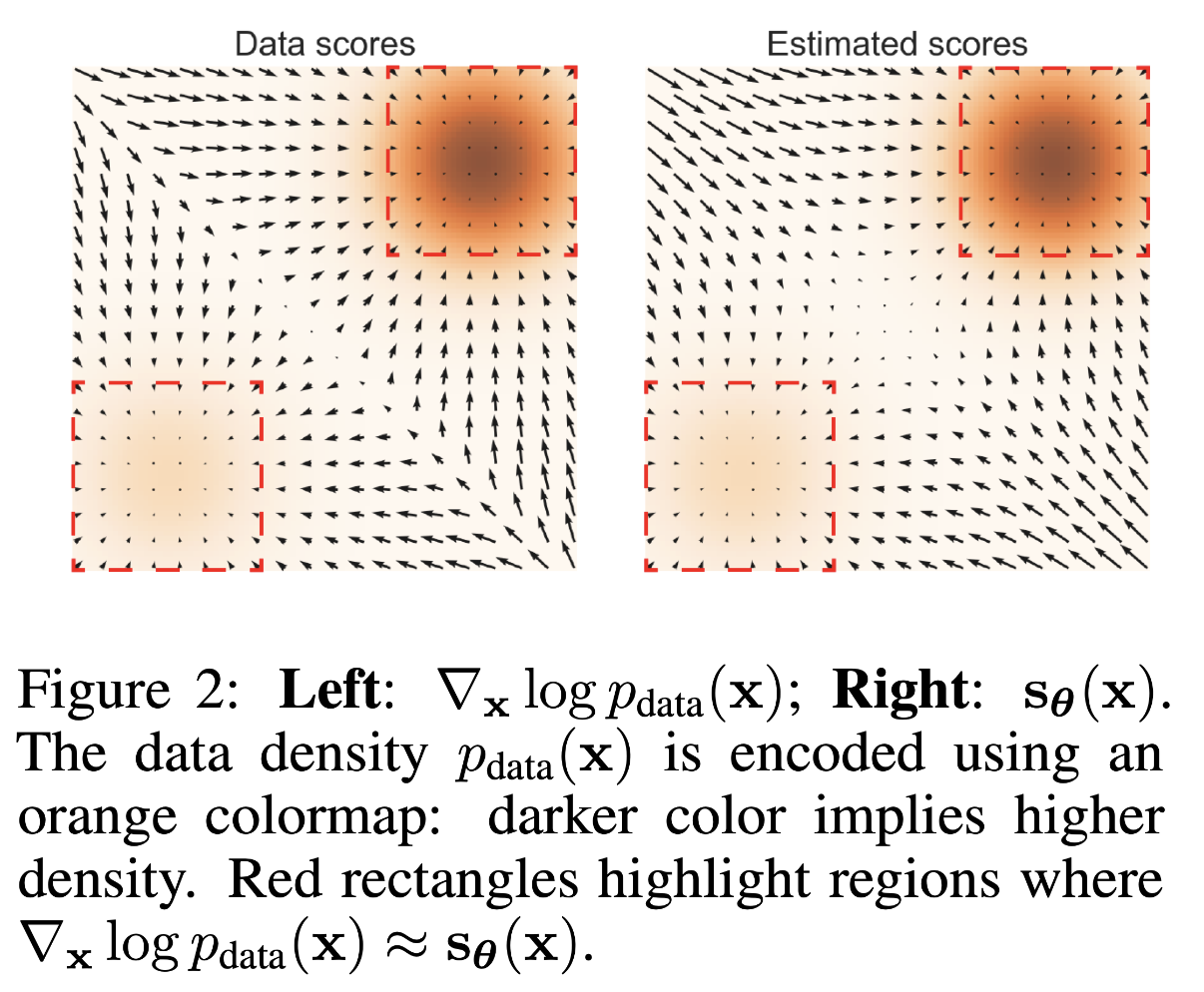
作者给出了一个案例，真实的数据分布为 $p_{\text {data }}=\frac{1}{5} \mathcal{N}((-5,-5), I)+\frac{4}{5} \mathcal{N}((5,5), I)$，这是一个双峰分布，峰值出现中图中的右上角和左下角。作者用矩形框圈定了真实 score 和模型预测 score 高度一致的区域，显然集中在密度比较高的橙色区域。

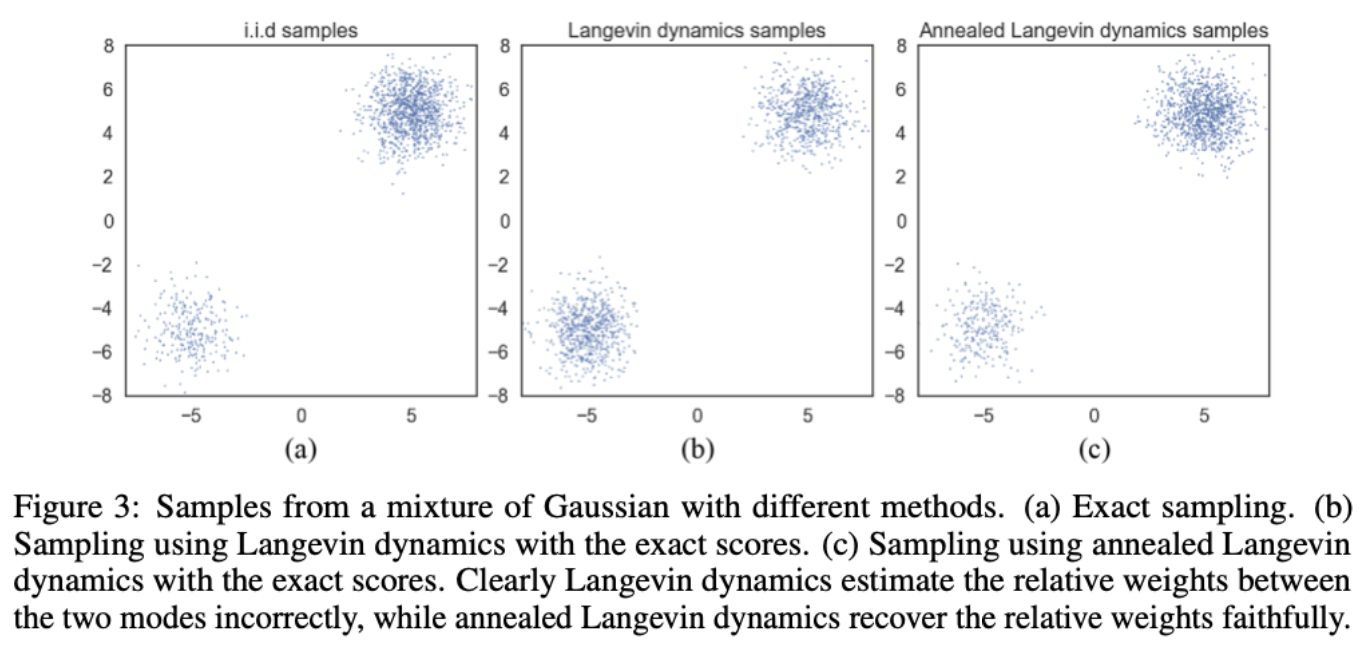
低密度区域还会影响朗之万采样的效果。具体而言，考虑混合分布 $p_{\text {data }}(\mathbf{x})=\pi p_1(\mathbf{x})+(1-\pi) p_2(\mathbf{x})$，其中融合的两个分布的支撑集不联通，对于处在 $p_1(\mathbf{x})$ 支撑集的样本，score为 $\nabla_{\mathbf{x}} \log p_{\text {data }}(x)=\nabla_{\mathbf{x}}\left(\log \pi+\log p_1(\mathbf{x})\right)=\nabla_{\mathbf{x}} \log p_1(\mathbf{x})$，对于处在 $p_2(\mathbf{x})$ 支撑集的样本，score 为 $\nabla_{\mathbf{x}} \log p_{\text {data }}(\mathbf{x})=\nabla_{\mathbf{x}}(\log(1-\pi)+\log p_2(\mathbf{x}))=\nabla_{\mathbf{x}} \log p_2(\mathbf{x})$ 。换句话说 $\nabla_{\mathbf{x}} \log p_{\text {data }}(\mathbf{x})$ 与融合权重 $\pi$ 无关。此时的朗之万采样结果将与 $\pi$ 无关。实践中，如果两个被融合的分布的支撑集被低密度区域连通，相关的问题一样会存在。为了验证上述现象，作者使用上图中得到的真实的 score 值，并使用朗之万动力学进行采样，得到的样本如下图（b）所示，显然，最终的样本并没有反应出两个分布的相对重要性。图（c）是使用新的采样方案得到的结果（下文介绍）。

1.2.5 Noise Conditional Score Networks

为解决上述的挑战（流形假设和低密度数据），作者提出：

• 分层加噪策略缓解数据分布稀疏的问题；
• 训练一个NCSN同时估计所有加噪层的 score。

具体而言，作者定义了一个噪声几何序列 \(\left\{\sigma_i\right\}_{i=1}^L\) 满足 \(\frac{\sigma_1}{\sigma_2}=\cdots=\frac{\sigma_{L-1}}{\sigma_L}>1\)。同时为了确保扰动后的数据尽可能充满整个数据空间，\(\sigma_1\) 需要足够大；同时 $\sigma_L$ 需要足够小，以确保对真实数据分布的干扰最小。扰动后的数据分布为 $q_\sigma(\mathbf{x}) \triangleq\int p_{\text {data }}(\mathbf{t}) \mathcal{N}\left(\mathbf{x} \mid \mathbf{t}, \sigma^2 I\right) \mathrm{d} \mathbf{t}$ 。对于任意的加噪层，作者训练一个条件score网络来逼近真实的扰动分布的score，即：

\[\forall \sigma \in\left\{\sigma_i\right\}_{i=1}^L: \mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, \sigma) \approx \nabla_{\mathbf{x}} \log q_\sigma(\mathbf{x}) \tag{1.3}\]

其中 $\mathbf{s}_\theta(\mathbf{x}, \sigma)$ 被称为 Noise Conditional Score Network (NCSN)。

考虑到 $\mathbf{s}_\theta(\mathbf{x}, \sigma)$ 的输出需要与输入 $\mathbf{x}$ 具备相同的尺寸，作者选择使用 U-Net 作为基础的神经网络结构。为了向网络注入条件信息 $\sigma_i$，作者使用了 conditional instance normalization 的改进版 CondInstanceNorm++。具体而言，传统的conditional instance normalization定义为：

\[\mathbf{z}_k=\gamma[i, k] \frac{\mathbf{x}_k-\mu_k}{s_k}+\beta[i, k], \tag{1.4}\]

其中 $\mathbf{x}_k$ 表示输入 feature map 的第 $k$ 个通道，$\mu_k$ 和 $s_k$ 为对应的期望和方差。$\gamma \in \mathbb{R}^{L \times C}$ 和 $\beta \in \mathbb{R}^{L \times C}$ 为可学习参数，$L$ 表示所加的噪声层数，$C$ 表示输入的 feature map 的通道数。$i$ 表示噪声 $\sigma$ 的索引。

作者认为 CondInstanceNorm 的不足在于，它完全删除了不同特征的原有的 $\mu_k$ 信息。这可能会导致生成的图像颜色发生偏移。为了修复这一点，作者提出 CondInstanceNorm++。首先计算出 $\mu_k$ 的期望和方差，表示为 $m$ 和 $v$（这里的期望和方差是基于 batch 维度计算的）。然后新增一组可学习参数 $\alpha \in \mathbb{R}^{L \times C}$ 实现解调的操作。最终的结构为：

\[\mathbf{z}_k=\gamma[i, k] \frac{\mathbf{x}_k-\mu_k}{s_k}+\beta[i, k]+\alpha[i, k] \frac{\mu_k-m}{v} \tag{1.5}\]

在具体实现中，作者选用条件高斯分布作为扰动核： $q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})=\mathcal{N}\left(\tilde{\mathbf{x}} \mid \mathbf{x}, \sigma^2 I\right)$，此时 $\nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})=-(\tilde{\mathbf{x}}-\mathbf{x}) / \sigma^2$，将其代入公式（1.1）：

\[\ell(\boldsymbol{\theta} ; \sigma) \triangleq \frac{1}{2} \mathbb{E}_{p_{\operatorname{tat}}(\mathbf{x})} \mathbb{E}_{\overline{\mathbf{x}} \sim \mathcal{N}\left(\mathbf{x}, \sigma^2 I\right)}\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}}, \sigma)+\frac{\tilde{\mathbf{x}}-\mathbf{x}}{\sigma^2}\right\|_2^2\right] . \tag{1.6}\]

聚合所有加噪层的优化目标，我们有：

\[\mathcal{L}\left(\boldsymbol{\theta} ;\left\{\sigma_i\right\}_{i=1}^L\right) \triangleq \frac{1}{L} \sum_{i=1}^L \lambda\left(\sigma_i\right) \ell\left(\boldsymbol{\theta} ; \sigma_i\right), \tag{1.7}\]

式中 $\lambda\left(\sigma_i\right)>0$ 为不同加噪层的加权系数。为了使不同加噪层的损失大小具备大致相当的数量级（数值稳定），作者令 $\lambda(\sigma)=\sigma^2$，加权后的 loss 数量级与每一层对应的 $\sigma_i$ 不再相关。

1.2.6 Annealed Langevin dynamics

在训练好NCSN后，我们就可以使用 annealed Langevin dynamics 来进行样本生成，如下图的算法1所示，采样过程首先基于一个简单的先验分布（如正态分布/均匀分布）初始化样本 $\tilde{\mathbf{x}}_0$，接着在每一个加噪层 $i$ 内使用朗之万采样器生成样本，当前层生成的样本将作为下一层样本的起点，即 $\tilde{\mathbf{x}}_0 \leftarrow \tilde{\mathbf{x}}_T$。每一层的朗之万迭代步长与当前层的噪声强度相关，噪声强度越大，步长越大，即 $\alpha_i \leftarrow \epsilon \cdot \sigma_i^2 / \sigma_L^2$。

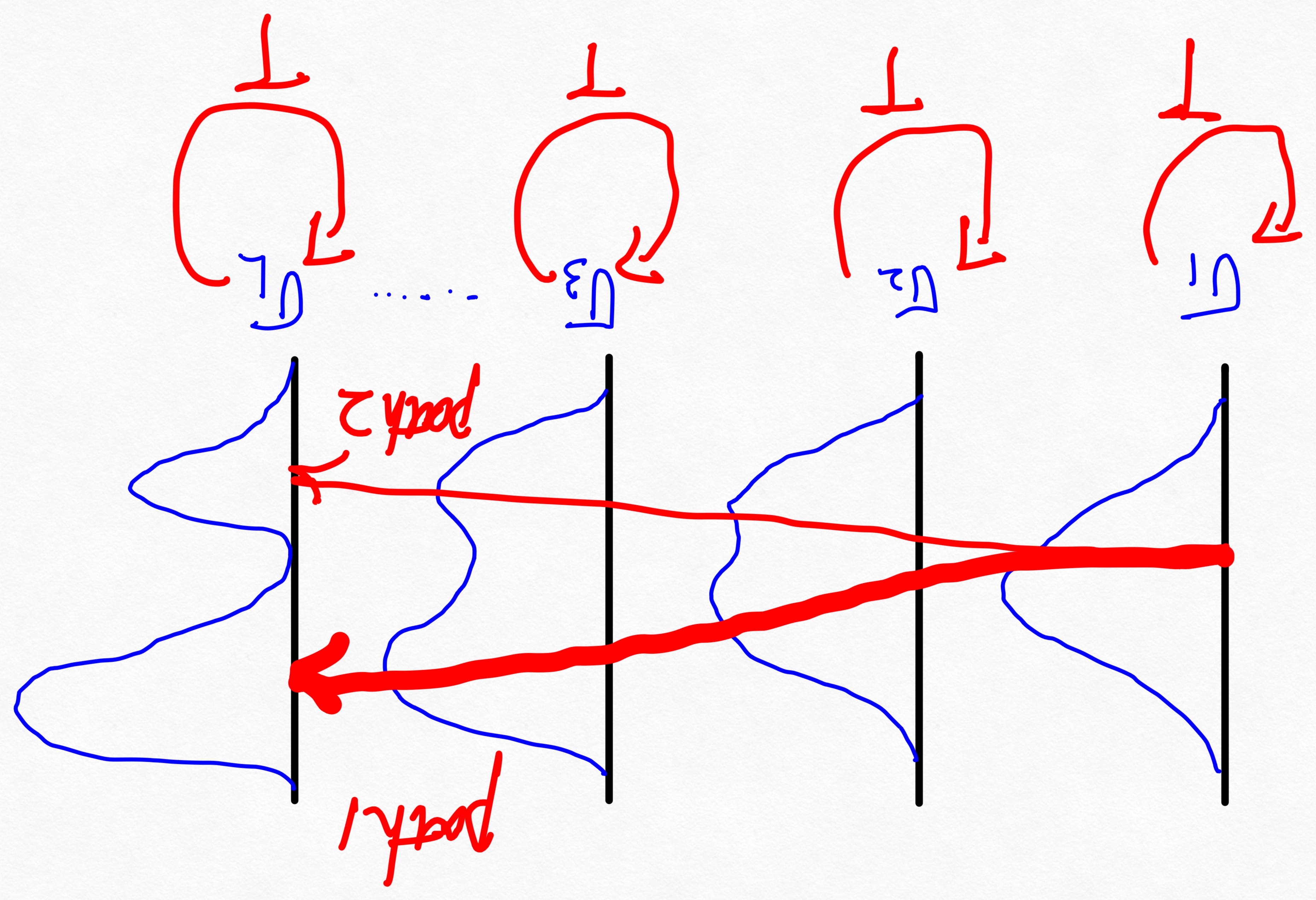
退火朗之万动力学采样为什么可以捕捉到混合分布的不同组分之间的相对权重呢？如下图所示，采样从$\sigma_1$ 对应最终的高斯分布开始，得到的样本大概率覆盖高斯分布的高密度区域。由于 $\sigma_2$ 层与 $\sigma_1$ 层的两个分布重合度高，所以来自于$\sigma_1$ 层的样本大概率也会落在 $\sigma_2$ 层的高密度区域。依次类推，样本的演进经过path1 的概率大于path2，所以退火朗之万动力学采样可以成功捕捉真实分布的混合权重。

1.3 相关结论

作者在 MNIST, CelebA, 和 CIFAR-10 三个数据集进行实验。对于 CelebA，图片首先 center-cropped 到 $140\times140$ 然后 resize 到 $32\times32$。所有图片像素被 rescale 到 $[0,1]$ 区间（所以作者在推理阶段，初始化的噪声来自于均匀分布，这与后来的主流的$[-1,1]$区间存在区别）。加噪层数设置为 $L=10$，$\sigma_1=1$，$\sigma_{10}=0.01$。推理阶段使用 $T=100$，$\epsilon=2 \times 10^{-5}$。初始噪声从==均匀分布==中采样得到。

1.3.1 可视化效果

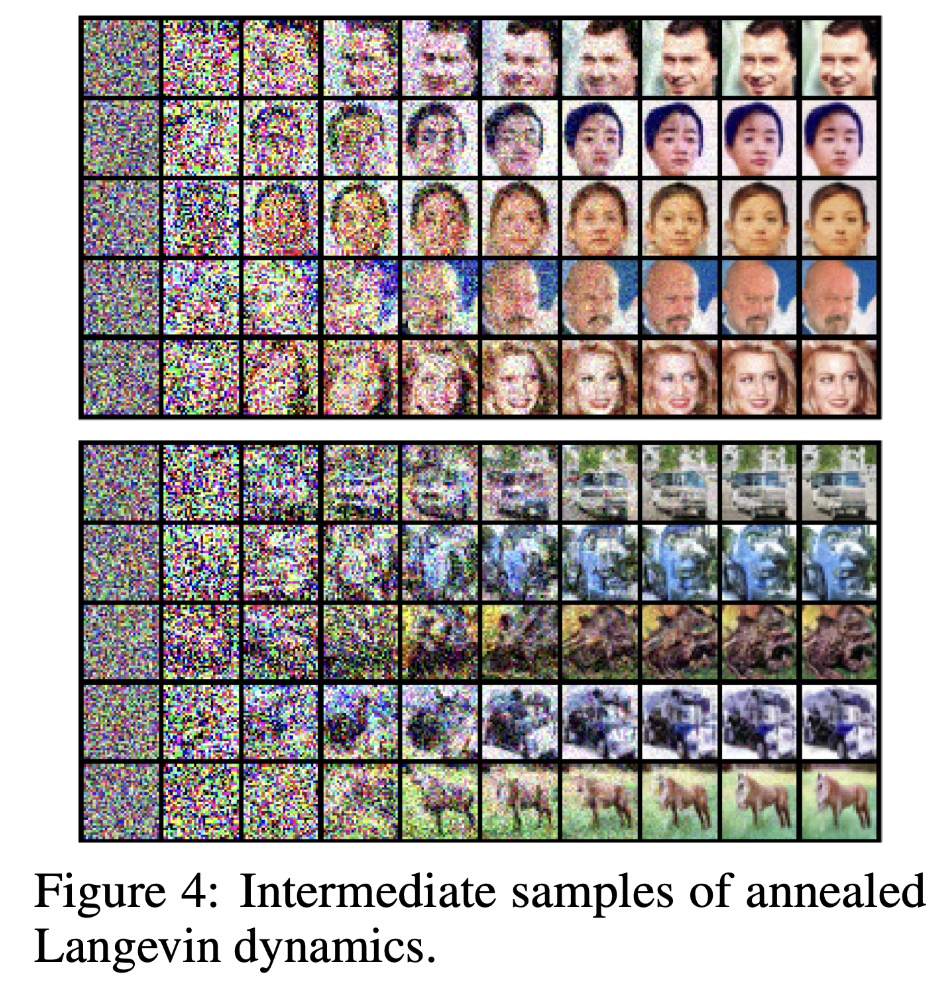
上图展示了退火朗之万采样器的中间结果，不难发现样本从完全噪声到正常图片的演变过程。

1.3.2 定量分析

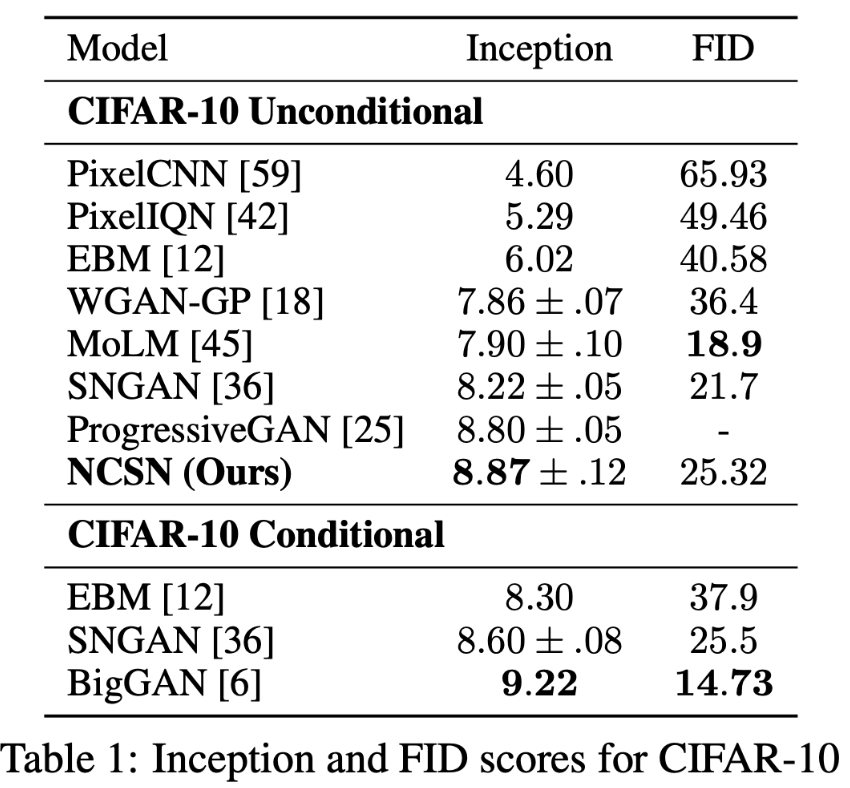
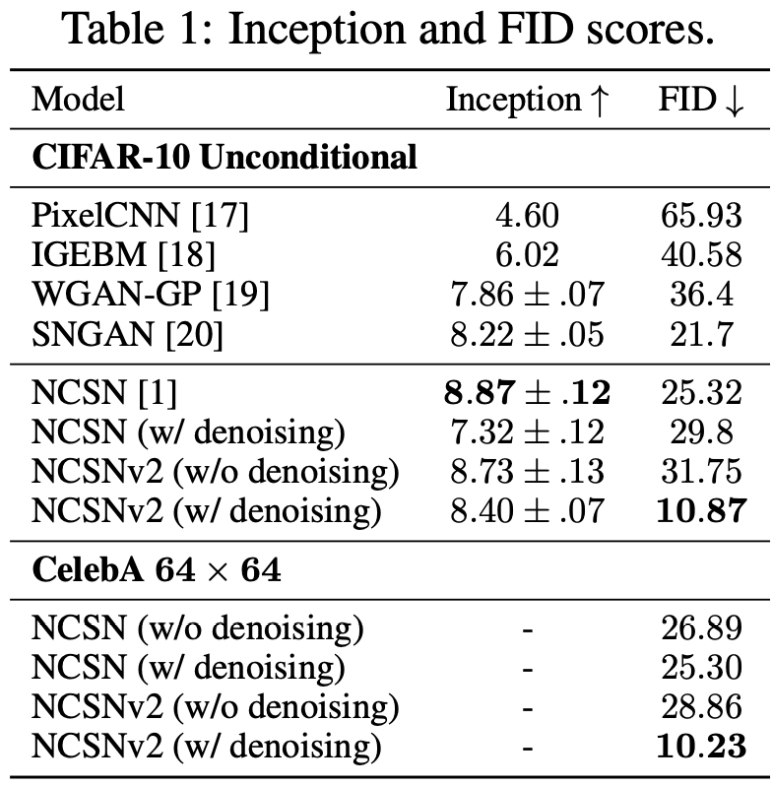
作为一个无条件模型，NCSN 实现了8.87的SOTA 感知 score，这比大多数类条件生成模型的值还要好。在CIFAR-10上的FID得分为25.32。

1.3.3 原文结论

We propose the framework of score-based generative modeling where we first estimate gradients of data densities via score matching, and then generate samples via Langevin dynamics. We analyze several challenges faced by a naïve application of this approach, and propose to tackle them by training Noise Conditional Score Networks (NCSN) and sampling with annealed Langevin dynamics. Our approach requires no adversarial training, no MCMC sampling during training, and no special model architectures. Experimentally, we show that our approach can generate high quality images that were previously only produced by the best likelihood-based models and GANs. We achieve the new state-of-the-art inception score on CIFAR-10, and an FID score comparable to SNGANs.

我们提出了 score-based generative modeling 框架，其中我们首先通过 score matching 估计数据密度的梯度，然后通过Langevin dynamics （朗之万动力学）生成样本。我们分析了这种方法的应用所面临的几个挑战，并建议通过训练噪声条件得分网络（Noise Conditional Score Networks，NCSN）和用退火朗之万动力学（annealed Langevin dynamics）进行采样来解决这些挑战。我们的方法不需要对抗性训练，训练过程中不需要MCMC采样，也不需要特殊的模型架构。实验表明，我们的方法可以生成以前只有最佳的 likelihood-based模型和GAN生成的高质量图像。我们在CIFAR-10数据上获得了SOAT的inception得分，FID得分与SNGAN相当。

2. Improved Techniques for Training Score-Based Generative Models

Improved Techniques for Training Score-Based Generative Models.Yang Song, and Stefano Ermon.In the 34th Conference on Neural Information Processing Systems, 2020.

2.1 要点概述

• Score-based 生成模型虽然可以生成高质量的样本，但训练图片仅局限在低分辨率（小于$32\times32$）
• 提供了一个新的理论分析，提高了 score-based 模型在高分辨率图片上的训练和推理性能
• 使用指数滑动平均对模型权重进行集成，提高稳定性。

2.2 深度解读

2.2.1 基础 score-based 模型的不足

在基础的 score-based模型中，作者使用了多层加噪的策略弥补训练数据分布稀疏的问题。推荐的加噪强度 ${\sigma_i}_{i=1}^L$ 在低分辨率 $32 \times 32$ 上表现良好，但不适用于更高分辨率的图片。其次，朗之万动力学采样策略在高分辨率图片上的生成表现也不佳。

2.2.2 如何设计每一层的加噪强度

在基础版本的模型中，不同层的加噪强度是一个几何序列，满足 $L=10, \sigma_1=1$，$\sigma_L=0.01$。其中最小的噪声强度 $\sigma_L=0.01 \ll 1$ 是合理的，因为越靠近真实分布的扰动强度越小。然而，作者发现以下的问题对NCSN在高分辨率图像上的成功至关重要：

• $\sigma_1=1$ 的设置是否合理；如果不合理，是否应该根据不同的数据集调整设置；
• 几何级数是个好的选择吗；
• $L=10$ 对于不同的数据集是否都是合理的，如果不是，多少加噪层数才是理想的？

2.2.2.1 设置初始噪声强度 $\sigma_1$

直觉上，初始噪声强度所在的分布是朗之万动力学采样的起点，为了确保最终采样的多样性，我们希望采样的起点没有特殊的倾向，换句话说，我们希望 $\sigma_1$ 足够的大。然而，更大的 $\sigma_1$ 将导致更多的加噪层数，进而导致推理时需要更多的迭代次数，样本生成的成本增加。作者提出了一种方法来合理地选择 $\sigma_1$。

假设真实数据分布 $p_{\text {data }}(\mathbf{x})$ 中的独立同分布样本为 ${\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \cdots, \mathbf{x}^{(N)}}$。 如果 $N$ 足够大，我们有 \(p_{\text {data }}(\mathbf{x}) \approx \hat{p}_{\text {data }}(\mathbf{x}) \triangleq \frac{1}{N} \sum_{i=1}^N \delta\left(\mathbf{x}=\mathbf{x}^{(i)}\right)\)。 如果我们使用扰动核 \(\mathcal{N}\left(\mathbf{0}, \sigma_1^2 \mathbf{I}\right)\) 对样本进行加噪，最后一层的经验分布为 \(\hat{p}_{\sigma_1}(\mathbf{x}) \triangleq \frac{1}{N} \sum_{i=1}^N p^{(i)}(\mathbf{x})\)，其中 \(p^{(i)}(\mathbf{x}) \triangleq \mathcal{N}\left(\mathbf{x} \mid \mathbf{x}^{(i)}, \sigma_1^2 \mathbf{I}\right)\)。 我们==需要避免初始化对样本生成的多样性有影响==，也就是说，不管我们的采样起点在哪，最终的样本可以到达任意一个真实数据。形式化的表述为，假设我们从分布 \(p^{(j)}(\mathbf{x})\) 初始化采样起点，我们希望采样的终点依然有可能是样本 \(\mathbf{x}_i\)， 其中 $i \neq j$。 而采样的路径变化由 score function \(\nabla_{\mathbf{x}} \log \hat{p}_{\sigma_1}(\mathbf{x})\) 决定。

命题1：令 \(\hat{p}_{\sigma_1}(\mathbf{x}) \triangleq \frac{1}{N} \sum_{i=1}^N p^{(i)}(\mathbf{x})\)，其中 \(p^{(i)}(\mathbf{x}) \triangleq \mathcal{N}\left(\mathbf{x} \mid \mathbf{x}^{(i)}, \sigma_1^2 \mathbf{I}\right)\)。令 \(r^{(i)}(\mathbf{x}) \triangleq \frac{p^{(i)}(\mathbf{x})}{\sum_{k=1}^N p^{(k)}(\mathbf{x})}\) ，此时的 score function 为 \(\nabla_{\mathbf{x}} \log \hat{p}_{\sigma_1}(\mathbf{x})=\sum_{i=1}^N r^{(i)}(\mathbf{x}) \nabla_{\mathbf{x}} \log p^{(i)}(\mathbf{x})\)。进一步，我们有

\[\mathbb{E}_{p^{(i)}(\mathbf{x})}\left[r^{(j)}(\mathbf{x})\right] \leq \frac{1}{2} \exp \left(-\frac{\left\|\mathbf{x}^{(i)}-\mathbf{x}^{(j)}\right\|_2^2}{8 \sigma_1^2}\right) \tag{2.1}\]

为了确保朗之万动力学采样器能容易地从 $p^{(i)}(\mathbf{x})$ 过渡到 $p^{(j)}(\mathbf{x})$，\(\mathbb{E}_{p^{(i)}(\mathbf{x})}\left[r^{(j)}(\mathbf{x})\right]\)不能太小，否则当初始化的样本 \(\mathbf{x} \sim p^{(i)}(\mathbf{x})\)， \(\nabla_{\mathbf{x}} \log \hat{p}_{\sigma_1}(\mathbf{x})=\sum_{k=1}^N r^{(k)}(\mathbf{x}) \nabla_{\mathbf{x}} \log p^{(k)}(\mathbf{x})\) 会忽略掉 \(p^{(j)}(\mathbf{x})\) 的分量。

由公式（2.1）可以发现，当 $\sigma_1$ 相较于 \(\left\|\mathbf{x}^{(i)}-\mathbf{x}^{(j)}\right\|_2\) 较小时， \(\mathbb{E}_{p^{(i)}(\mathbf{x})}\left[r^{(j)}(\mathbf{x})\right]\) 指数衰减的速度更快。所以，$\sigma_1$ 在数值上与训练样本中的最大成对距离相当，以促进朗之万动力学在不同样本间的转换，从而提高样本多样性。

技巧1：（初始加噪尺度）选择的 $\sigma_1$ 与所有训练数据点对之间的最大欧几里德距离相当。

2.2.2.2 设置中间层的加噪强度

一个很直观的感觉是，相邻的两个扰动分布应该尽可能的重合。为了给出理论层面的指导，作者考虑单个样本的情况，即 $\forall 1 \leq i \leq L: p_{\sigma_i}(\mathbf{x})=\mathcal{N}\left(\mathbf{x} \mid \mathbf{0}, \sigma_i^2\right)$。考虑到 $\mathbf{x}$ 一般是一个高维数据，作者将 $p_{\sigma_i}(\mathbf{x})$ 分解到超球面坐标 $p(\phi) p_{\sigma_i}(r)$，其中 $r$ 和 $\phi$ 表示 $\mathbf{x}$ 的径向和周向坐标。因为 $p_{\sigma_i}(\mathbf{x})$ 是一个各项同性的高斯分布，所以周向分量 $p(\boldsymbol{\phi})$ 在不同的加噪层共享。对于 $p_{\sigma_i}(r)$，我们有：

命题2：令 $\mathbf{x} \in \mathbb{R}^D \sim \mathcal{N}\left(\mathbf{0}, \sigma^2 \mathbf{I}\right)$，$r=|\mathbf{x}|_2$。

\[p(r)=\frac{1}{2^{D / 2-1} \Gamma(D / 2)} \frac{r^{D-1}}{\sigma^D} \exp \left(-\frac{r^2}{2 \sigma^2}\right) \text { and } r-\sqrt{D} \sigma \xrightarrow{d} \mathcal{N}\left(0, \sigma^2 / 2\right) \text { when } D \rightarrow \infty \text {. } \tag{2.2}\]

考虑到图片的维度可能是几千到几百万，所以以下的近似是合理的 $p(r) \approx \mathcal{N}\left(r \mid \sqrt{D} \sigma, \sigma^2 / 2\right)$。所以为简化分析，令 $p_{\sigma_i}(r)=\mathcal{N}\left(r \mid m_i, s_i^2\right)$，其中 $m_i \triangleq \sqrt{D} \sigma_i$，$s_i^2 \triangleq \sigma_i^2 / 2$。

我们的目标是确保 $p_{\sigma_i}(\mathbf{x})$ 覆盖 $p_{\sigma_{i-1}}(\mathbf{x})$ 的高密度区域。考虑到 $p(\phi)$ 在不同的加噪层是共享的，我们只需要保证 \(p_{\sigma_i}(r)\) 覆盖 $p_{\sigma_{i-1}}(r)$ 的高密度区域。后者的高密度区域集中在区间 \(\mathcal{I}_{i-1} \triangleq\left[m_{i-1}-3 s_{i-1}, m_{i-1}+3 s_{i-1}\right]\) （3-sigma准则）。所以我们希望在这个区域内，\(p_{\sigma_i}(r)\) 的取值也能保持一个相对较大的常数，即

\[p_{\sigma_i}\left(r \in \mathcal{I}_{i-1}\right)=\Phi\left(\sqrt{2 D}\left(\gamma_i-1\right)+3 \gamma_i\right)-\Phi\left(\sqrt{2 D}\left(\gamma_i-1\right)-3 \gamma_i\right)=C \tag{2.3}\]

其中 $C>0$ 对于所有的 $1<i \leq L$ 满足。$\gamma_i \triangleq \sigma_{i-1} / \sigma_i$，$\Phi(\cdot)$ 表示标准高斯分布的CDF（累积概率函数）。这个选择意味着 $\gamma_2=\gamma_3=\cdots \gamma_L$，所以 ${\sigma_i}_{i=1}^L$ 是一个几何序列。理想状态下，我们希望设置足够多的加噪层数使得 $C \approx 1$。然而，太多的加噪层会增加推理的时间成本。另一方面，在原先的设置中，$L=10$（对于$32 \times 32$图像）可以说太小了。为了达到平衡，作者令 $C \approx 0.5$。

技巧2：（中间加噪尺度）选择 ${\sigma_i}_{i=1}^L$ 为几何序列，相邻尺度比例为常数 $\gamma$，该常数满足 $ \Phi(\sqrt{2 D}(\gamma-1)+3 \gamma)-\Phi(\sqrt{2 D}(\gamma-1)-3 \gamma) \approx 0.5 $。

2.2.3 如何注入噪声条件信号

如式（1.5）所示，在基础的方案中，噪声是通过引入CondInstanceNorm++层实现注入的。其中引入了三个可学习参数矩阵 $\gamma,\beta,\alpha$，每一个行向量对应一个噪声层。对于更高的分辨率图片，需要更大的 $\sigma_1$ 和更多的加噪层数。这会导致参数矩阵越大越大，同时，如果网络结构中没有 normalization 层，NCSN 将不再适用。

作者提出了一种替代方案。对于一个训练完成的 NCSN，\(\left\|\mathbf{s}_\theta(\mathbf{x}, \sigma)\right\|_2 \propto 1 / \sigma\)。基于这个分析，作者通过用 $1 / \sigma$ 重新缩放无条件得分网络 \(\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})\) 的输出来注入噪声条件信息。

技巧3：（注入噪声信息）用 \(\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, \sigma)=\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}) / \sigma\) 的方式重参数化 NCSN，其中 \(\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x})\) 表示一个无条件score网络。

2.2.4 配置退火朗之万动力学采样

在早先的版本中，作者指定了推理时的配置 $\epsilon=2 \times 10^{-5}$ 和 $T=100$。但不同的噪声层是否适配同样的采样配置呢？

为了获得一些理论层面的指导，作者以单样本为例，此时 $\left.p_{\sigma_i}(\mathbf{x})=\mathcal{N}\left(\mathbf{x} \mid \mathbf{0}, \sigma_i^2 \mathbf{I}\right)\right)$。退火朗之万动力学的操作为，从分布 $p_{\sigma_{i-1}}(\mathbf{x})$ 初始化采样起点，然后使用朗之万动力学采样得到服从 $p_{\sigma_i}(\mathbf{x})$ 的样本，其中 $\sigma_{i-1}>\sigma_i$。具体而言，更新的机制为 \(\mathbf{x}_{t+1} \leftarrow \mathbf{x}_t+\alpha \nabla_{\mathbf{x}} \log p_{\sigma_i}\left(\mathbf{x}_t\right)+\sqrt{2 \alpha} \mathbf{z}_t\)，其中 \(\mathbf{x}_0 \sim p_{\sigma_{i-1}}(\mathbf{x})\)，\(\mathbf{z}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)。$\mathbf{x}_T$ 可以有一个闭式解：

命题3：令 $\gamma=\frac{\sigma_{i-1}}{\sigma_i}$。对于 $\alpha=\epsilon \cdot \frac{\sigma_i^2}{\sigma_L^2}$，我们有 $\mathbf{x}_T \sim \mathcal{N}\left(\mathbf{0}, s_T^2 \mathbf{I}\right)$，其中：

\[\frac{s_T^2}{\sigma_i^2}=\left(1-\frac{\epsilon}{\sigma_L^2}\right)^{2 T}\left(\gamma^2-\frac{2 \epsilon}{\sigma_L^2-\sigma_L^2\left(1-\frac{\epsilon}{\sigma_L^2}\right)^2}\right)+\frac{2 \epsilon}{\sigma_L^2-\sigma_L^2\left(1-\frac{\epsilon}{\sigma_L^2}\right)^2} . \tag{2.4}\]

根据技巧2，${\sigma_i}_{i=1}^L$ 是一个几何序列。考虑到 $\gamma$ 在不同噪声层是共享的，所以 $s_T^2 / \sigma_i^2$ 在不同的加噪层是相等的。进一步，$s_T^2 / \sigma_i^2$ 的大小与维度 $D$ 无显式依赖关系。

为了使退火朗之万动力学采样更容易捕捉混合权重，我们希望 $s_T^2 / \sigma_i^2$ 接近$1$，并适用于所有噪声尺度。我们可以通过优化 $\epsilon$ 和 $T$ 使公式（2.4）和 $1$ 之间的差最小。不幸的是，这通常会导致不必要的很大的 $T$ 值，采样成本因此增加。作为替代方案，我们建议首先根据合理的计算预算选择 $T$（通常 $T\times L$ 为几千，就是朗之万动力学采样的迭代次数），然后基于 $\epsilon$ 优化式（2.4）与 $1$ 之间的差距 。

技巧4： （选择 $T$ 和 $\epsilon$）选择推理预算允许的最大值 $T$，然后选择 $\epsilon$，使得公式（2.4）最大程度地接近1。

2.2.5 滑动平均提高稳定性

为了弥补训练过程中的不稳定性，作者提出使用指数滑动平均（EMA）的策略来稳定模型的性能。令 \(\boldsymbol{\theta}_i\) 表示第 $i$ 次训练迭代后的参数，\(\boldsymbol{\theta}^{\prime}\) 为一份独立的参数 copy。使用 \(\boldsymbol{\theta}^{\prime} \leftarrow m \boldsymbol{\theta}^{\prime}+(1-m) \boldsymbol{\theta}_i\) 更新copy 的参数。推理时使用 \(\mathbf{s}_{\boldsymbol{\theta}^{\prime}}(\mathbf{x}, \sigma)\)。EMA可以有效地稳定FID，消除伪影，并在大多数情况下给出更好的FID分数。

技巧5：推理时使用指数滑动平均集成的模型。

2.2.6 NCSNv2

将所有的技巧集成后，作者得到了 NCSNv2 模型。

2.3 相关结论

2.3.1 定量分析

NCSN 和 NCSNv2 在 CIFAR-10 $32\times 32$ 和 CelebA $64\times 64$ 的对比结果。

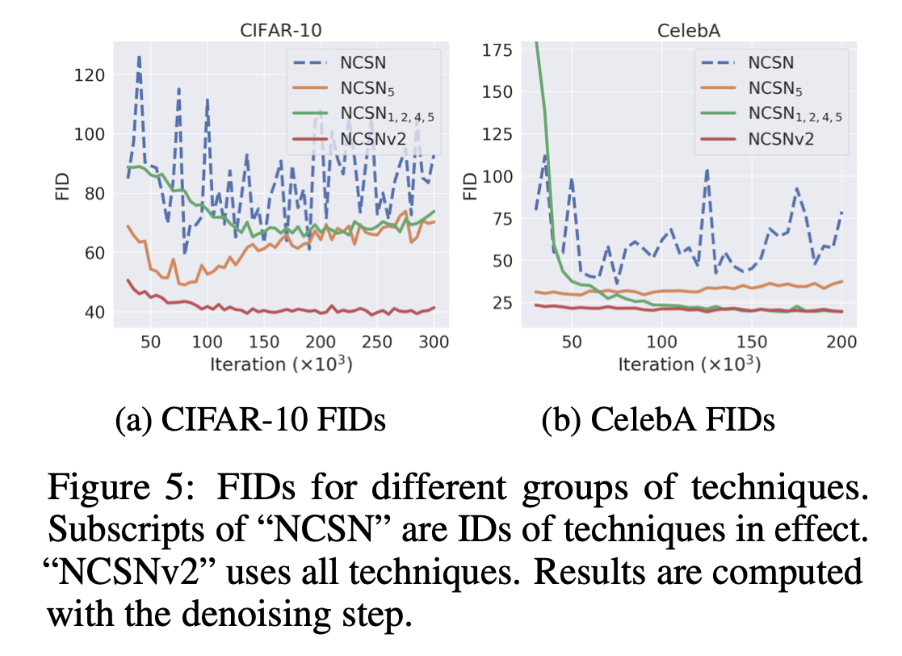
上图展示了每训练 5000 步在1000个样本上的 FIDs（包含 denoising 步骤），其中 denoising 步骤是指，在原有的朗之万采样结尾，新增一步降噪的步骤，如下图展示的算法，第9行可以额外提高 FIDs。

更多样本上的测试结果为：

2.3.2 原文结论

Motivated by both theoretical analyses and empirical observations, we propose a set of techniques to improve score-based generative models. Our techniques significantly improve the training and sampling processes, lead to better sample quality, and enable high-fidelity image generation at high resolutions. Although our techniques work well without manual tuning, we believe that the performance can be improved even more by fine-tuning various hyper-parameters. Future directions include theoretical understandings on the sample quality of score-based generative models, as well as alternative noise distributions to Gaussian perturbations.

受理论分析和实证观察的启发，我们提出了一套改进基于分数的生成模型的技术。我们的技术显著改善了训练和采样过程，提高了样本质量，并能够以高分辨率生成高保真图像。尽管我们的技术在没有手动调整的情况下工作良好，但我们相信，通过微调各种超参数，性能可以得到更大的提高。未来的方向包括对基于分数的生成模型的样本质量的理论理解，以及高斯扰动的替代噪声分布。

3. SCORE-SDE

Score-Based Generative Modeling through Stochastic Differential Equations. Yang Song, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, and Ben Poole. In the 9th International Conference on Learning Representations, 2021..Outstanding Paper Award

3.1 要点概述

• 两种成功的概率生成模型包含2个重要环节：前向逐步加噪以及学习如何逆向降噪。Score matching with Langevin dynamics (SMLD) 学习分布的 score ，并利用这个score生成样本；而Denoising diffusion probabilistic modeling (DDPM) 学习每一个降噪步骤中的概率分布（高斯分布）参数。本质上，后者其实也是学习分布的 score，两者实际上是等价的。作者统一称之为 score-based generative models；
• 之前的讨论只局限在离散空间，作者将分析拓展到连续空间。具体而言，加噪的过程由一个预设好的随机微分方程（SDE）定义，该方程与训练数据无关且不包含需要学习的参数；
• 生成过程对应 reverse-time SDE，它由 前向SDE的形式 和 分布的score 决定。通过训练神经网络估计score，可以得到reverse-time SDE。在数值SDE求解器的辅助下，我们便可以实现样本生成。具体过程如下图所示。

3.2 深度解读

3.2.1 模型回顾

3.2.1.1 DENOISING SCORE MATCHING WITH LANGEVIN DYNAMICS (SMLD)

令 $p_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}):=\mathcal{N}\left(\tilde{\mathbf{x}} ; \mathbf{x}, \sigma^2 \mathbf{I}\right)$ 为一个扰动核，扰动后的边际分布为 $p_\sigma(\tilde{\mathbf{x}}):=\int p_{\text {data }}(\mathbf{x}) p_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x}) \mathrm{dx}$，其中 $p_{\text {data }}(\mathbf{x})$ 表示未知的数据分布。考虑一个加噪序列 $\sigma_{\min }=\sigma_1<\sigma_2<\cdots<\sigma_N=\sigma_{\max }$ 。其中 $\sigma_{\min }$ 足够小，使得 $p_{\sigma_{\mathrm{min}}}(\mathbf{x}) \approx p_{\text {data }}(\mathbf{x})$；$\sigma_{\max }$ 足够大，使得 $p_{\sigma_{\max }}(\mathbf{x}) \approx \mathcal{N}\left(\mathbf{x} ; \mathbf{0}, \sigma_{\max }^2 \mathbf{I}\right)$。NCSN，即 $\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, \sigma)$，基于 denoising score matching 的策略训练如下的目标函数：

\[\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg \min } \sum_{i=1}^N \sigma_i^2 \mathbb{E}_{p_{\mathrm{data}}(\mathbf{x})} \mathbb{E}_{p \sigma_i}(\tilde{\mathbf{x}} \mid \mathbf{x})\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}\left(\tilde{\mathbf{x}}, \sigma_i\right)-\nabla_{\tilde{\mathbf{x}}} \log p_{\sigma_i}(\tilde{\mathbf{x}} \mid \mathbf{x})\right\|_2^2\right] \tag{3.1}\]

给定足够数据样本和模型拟合能力，最优解 \(\mathbf{s}_{\boldsymbol{\theta}^*}(\mathbf{x}, \sigma)\) 将与 \(\nabla_{\mathbf{x}} \log p_\sigma(\mathbf{x})\) 匹配。对于采样过程，在每一个加噪层 $i$，执行 $M$ 步朗之万动力学采样：

\[\mathbf{x}_i^m=\mathbf{x}_i^{m-1}+\epsilon_i \mathbf{s}_{\theta^*}\left(\mathbf{x}_i^{m-1}, \sigma_i\right)+\sqrt{2 \epsilon_i} \mathbf{z}_i^m, \quad m=1,2, \cdots, M, \tag{3.2}\]

其中 $\epsilon_i>0$ 表示迭代步长，$\mathbf{z}_i^m$ 表示标准正态分布。

3.2.1.2 DENOISING DIFFUSION PROBABILISTIC MODELS (DDPM)

在DDPM中，同样预设了一个加噪序列 $0<\beta_1, \beta_2, \cdots, \beta_N<1$。对于每一个训练样本 \(\mathbf{x}_0 \sim p_{\text {data }}(\mathbf{x})\)，构造一个离散马尔可夫链 \({\mathbf{x}_0, \mathbf{x}_1, \cdots, \mathbf{x}_N}\)，马尔可夫的状态转移函数定义为 \(p\left(\mathbf{x}_i \mid \mathbf{x}_{i-1}\right)=\mathcal{N}\left(\mathbf{x}_i ; \sqrt{1-\beta_i} \mathbf{x}_{i-1}, \beta_i \mathbf{I}\right)\)，因此我们有 \(p_{\alpha_i}\left(\mathbf{x}_i \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_i ; \sqrt{\alpha_i} \mathbf{x}_0,\left(1-\alpha_i\right) \mathbf{I}\right)\)，其中 \(\alpha_i:=\prod_{j=1}^i\left(1-\beta_j\right)\)。类似于 SMLD，DDPM 中的扰动分布为 \(p_{\alpha_i}(\tilde{\mathbf{x}}):=\int p_{\text {data }}(\mathbf{x}) p_{\alpha_i}(\tilde{\mathbf{x}} \mid \mathbf{x}) \mathrm{d} \mathbf{x}\)。

DDPM 的逆向过程参数化为 \(p_{\boldsymbol{\theta}}\left(\mathbf{x}_{i-1} \mid \mathbf{x}_i\right)=\mathcal{N}\left(\mathbf{x}_{i-1} ; \frac{1}{\sqrt{1-\beta_i}}\left(\mathbf{x}_i+\beta_i \mathbf{s}_{\boldsymbol{\theta}}\left(\mathbf{x}_i, i\right)\right), \beta_i \mathbf{I}\right)\)。为了优化网络 \(\mathbf{s}_{\boldsymbol{\theta}}\left(\mathbf{x}_i, i\right)\)，DDPM 使用证据下确界（ELBO）作为优化目标，并最终可写成如下的形式（此处作者忽略了一些中间推导过程，为的是强调与SMLD优化目标的一致性）：

\[\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg \min } \sum_{i=1}^N\left(1-\alpha_i\right) \mathbb{E}_{p_{\text {data }}(\mathbf{x})} \mathbb{E}_{p_{\alpha_i}(\tilde{\mathbf{x}} \mid \mathbf{x})}\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}}, i)-\nabla_{\tilde{\mathbf{x}}} \log p_{\alpha_i}(\tilde{\mathbf{x}} \mid \mathbf{x})\right\|_2^2\right] . \tag{3.3}\]

得到最优解 \(\mathbf{s}_{\boldsymbol{\theta}^*}(\mathbf{x}, i)\) 后，采样过程从高斯噪声 \(\mathbf{x}_N \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\) 开始，并按照逆向马尔可夫链的方式进行迭代更新

\[\mathbf{x}_{i-1}=\frac{1}{\sqrt{1-\beta_i}}\left(\mathbf{x}_i+\beta_i \mathbf{s}_{\theta^*}\left(\mathbf{x}_i, i\right)\right)+\sqrt{\beta_i} \mathbf{z}_i, \quad i=N, N-1, \cdots, 1 . \tag{3.4}\]

作者称上述采样方式为 始祖采样（ancestral sampling），因为这相当于从图模型中执行始祖采样。

不难发现 DDPM 的优化目标与 SMLD 的优化目标是一致的。所以本质上，DDPM 实际上也是在估计扰动分布的 score 值。

抛开数学层面的具体推导，根据定义，score 是指（对数）概率分布关于样本 $\mathbf{x}$ 的梯度，score指向的方向即为 $p(\mathbf{x})$ 增加的方向，而 $p(\mathbf{x})$ 较大的区域就是正常样本所在的区域。同样，根据一张含噪样本预测加在此含噪样本上的噪声，该噪声实际上也是指向通往正常（无噪声）样本的更新路径（因为含噪声样本减去噪声就是去噪后的正常样本）。

3.2.2 SDEs 框架下的 score-based 生成模型

3.2.2.1 利用 SDEs 对数据进行扰动

作者的目标是构建一个扩散过程 ${\mathbf{x}(t)}_{t=0}^T$，其中 $t \in[0, T]$ 是一个连续变量，$\mathbf{x}(0) \sim p_0$ ，即真实的数据分布，$\mathbf{x}(T) \sim p_T$，即采样的起点分布。这种扩散过程可以被建模为 Itô SDE 的解：

\[\mathrm{d} \mathbf{x}=\mathbf{f}(\mathbf{x}, t) \mathrm{d} t+g(t) \mathrm{d} \mathbf{w} \tag{3.5}\]

其中 $\mathbf{w}$ 是一个标准Wiener process（也就是布朗运动），$\mathbf{f}(\cdot, t): \mathbb{R}^d \rightarrow \mathbb{R}^d$ 是 $\mathbf{x}(t)$ 的 偏移系数（drift），输出是一个矢量；$g(\cdot): \mathbb{R} \rightarrow \mathbb{R}$ 是一个标量函数，被称为 $\mathbf{x}(t)$ 的 扩散（diffusion）系数。事实上，前文提到的 SMLD 和 DDPM 是SDEs的2种不同离散化方式。

3.2.2.2 利用 reverse SDEs 对数据进行采样

前向 SDEs 的逆过程 reverse-time SDE 定义为：

\[\mathrm{d} \mathbf{x}=\left[\mathbf{f}(\mathbf{x}, t)-g(t)^2 \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\right] \mathrm{d} t+g(t) \mathrm{d} \overline{\mathbf{w}} \tag{3.6}\]

其中 $\overline{\mathbf{w}}$ 为时间从 $T$ 到 $0$ 的标准维纳过程，$\mathrm{d} t$ 表示无限小的可忽略的时间步长。不难发现逆向SDEs 实际上也是一个 SDEs。如果我们已知所有时间 $t$ 下的score $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$ 。我们便可以从起始分布 $p_T$ 采样到最终的数据分布 $p_0$。

3.2.2.3 估计 SDE 中的 score

根据在离散场景下的优化目标，为了估计在连续场景下的 score 值，我们需要训练一个 time-dependent score-based 模型 $\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}, t)$，沿用 denoising score matching 的优化目标（其他的优化方式也是可行的）：

\[\boldsymbol{\theta}^*=\underset{\boldsymbol{\theta}}{\arg \min } \mathbb{E}_t\left\{\lambda(t) \mathbb{E}_{\mathbf{x}(0)} \mathbb{E}_{\mathbf{x}(t) \mid \mathbf{x}(0)}\left[\left\|\mathbf{s}_{\boldsymbol{\theta}}(\mathbf{x}(t), t)-\nabla_{\mathbf{x}(t)} \log p_{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0))\right\|_2^2\right]\right\} . \tag{3.7}\]

其中 \(\lambda:[0, T] \rightarrow \mathbb{R}_{>0}\) 是加权函数，$t$ 均匀分布在区间 $[0, T]$。\(\mathbf{x}(0) \sim p_0(\mathbf{x})\)，\(\mathbf{x}(t) \sim p_{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0))\)。上式中还需要确定转移核 \(p_{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0))\) 的形式。如果式（17）中的 $\mathbf{f}(\cdot, t)$ 是仿射变换，则转移核始终是一个高斯分布，对应的期望和方差通常有闭式解。对于更一般的 SDEs，需要使用其他方式得到 \(p_{0 t}(\mathbf{x}(t) \mid \mathbf{x}(0))\)。

3.2.2.4 VE和VP SDEs

如前文所述，SMLD 和 DDPM 实际上可以看成SDEs的两种不同的离散化方式。

在SMLD 中，每一个加噪层使用的扰动核为 $p_{\sigma_i}\left(\mathbf{x} \mid \mathbf{x}_0\right)$，而对应的扰动样本 $\mathbf{x}_i$ 也可以通过如下的马尔可夫链获得：

\[\mathbf{x}_i=\mathbf{x}_{i-1}+\sqrt{\sigma_i^2-\sigma_{i-1}^2} \mathbf{z}_{i-1}, \quad i=1, \cdots, N \tag{3.8}\]

上式中的 $N$ 为加噪的层数。\(\mathbf{z}_{i-1} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)。当 \(N \rightarrow \infty\)，\(\left\{\sigma_i\right\}_{i=1}^N\) 将成为关于时间 $t$ 的函数 $\sigma(t)$，而 \(\mathbf{z}_i\) 变成 \(\mathbf{z}(t)\)。马尔可夫链 \(\left\{\mathbf{x}_i\right\}_{i=1}^N\) 将变成一个连续的随机过程 \(\{\mathbf{x}(t)\}_{t=0}^1\)，此处的时间 $t$ 已经通过除以 $T$ 的方式将值域调整到 $[0,1]$。此时的过程 \(\{\mathbf{x}(t)\}_{t=0}^1\) 由如下的SDE定义

\[\mathrm{d} \mathbf{x}=\sqrt{\frac{\mathrm{d}\left[\sigma^2(t)\right]}{\mathrm{d} t}} \mathrm{dw} \tag{3.9}\]

同样，对于DDPM中的扰动核 \(\left\{p_{\alpha_i}\left(\mathbf{x} \mid \mathbf{x}_0\right)\right\}_{i=1}^N\)，扰动样本 \(\mathbf{x}_i\) 对应的离散马尔可夫链为

\[\mathbf{x}_i=\sqrt{1-\beta_i} \mathbf{x}_{i-1}+\sqrt{\beta_i} \mathbf{z}_{i-1}, \quad i=1, \cdots, N . \tag{3.10}\]

当 $N \rightarrow \infty$，上式将对应如下的 SDE（证明参考原文附录B）

\[\mathrm{d} \mathbf{x}=-\frac{1}{2} \beta(t) \mathbf{x} \mathrm{d} t+\sqrt{\beta(t)} \mathrm{d} \mathbf{w} . \tag{3.11}\]

可见，SMLD 和 DDPM 在连续时间的设定下，都可以写成SDE 的形式，所不同的是前者没有 drift 项，因此，随着扩散过程的进行，样本的方差会不断增加，因此也被称为 Variance Exploding (VE) SDE；而DDPM对应的SDE形式包含 drift 项，所以如果初始的分布方差为1，则在扩散过程中的中间分布的方差也可以保持在1，因此也被称为 Variance Preserving (VP) SDE。当然，不论是 VE SDEs 还是 VP SDEs，偏移系数都是仿射变换（前者为0），所以转移核都是高斯分布，这使得求解过程变得简单。

3.2.3 reverse-time SDEs 框架下的采样器

在前面的章节中，我们论证了SMLD 和 DDPM 在连续时间的设定下，其加噪过程都可以统一在 SDEs 的框架下。本节，将介绍通过 reverse-time SDEs 的离散化所得到的不同的采样过程。

通过离散化reverse-time SDEs，作者提出了一种 reverse diffusion samplers 。在正式介绍之前，我们首先梳理一下已有的采样方法：

	DDPM (VP SDEs)	SMLD (VE SDEs)
ancestral sampling	✅	❌
langevin dynamics	❌	✅

3.2.3.1 predictor-corrector 采样框架

两种采样方法区别在于，ancestral sampling 实际上是在不同的加噪层进行样本的更新（也就是作者说的“预测器 predictor”），而 langevin dynamics 是在同一加噪层内对样本进行矫正（也就是作者说的“矫正器 corrector”）。基于此，作者提出一种将两个过程组合起来的采样器，即 predictor-corrector 框架（如下图所示）。

在此采样框架下，ancestral sampling 有预测器而没有矫正器，langevin dynamics 有矫正器而没有预测器。（注：按照原文的说法，ancestral sampling 的矫正器是一个恒等映射，langevin dynamics 的预测器是一个恒等映射）。

已知 ancestral sampling 是 reverse-time VP SDE 的一种离散化实现（参考附录 E），但要对其他 SDEs 推导出 ancestral sampling 却没那么容易。基于此，作者提出一种适配于 reverse-time VP SDEs 和 reverse-time VE SDEs 的离散化实现，即 reverse diffusion samplers，也就是 predictor-corrector 采样器中的predictor 部分。

对应于 DDPM，reverse diffusion samplers 的定义为（推导过程参考文章附录E）：

\[\mathbf{x}_i=\left(2-\sqrt{1-\beta_{i+1}}\right) \mathbf{x}_{i+1}+\beta_{i+1} \mathbf{s}_{\theta^*}\left(\mathbf{x}_{i+1}, i+1\right)+\sqrt{\beta_{i+1}} \mathbf{z}_{i+1} . \tag{3.12}\]

对于 SMLD，reverse diffusion samplers 定义为：

\[\mathbf{x}_{i-1}=\mathbf{x}_i+\left(\sigma_i^2-\sigma_{i-1}^2\right) \mathbf{s}_{\theta^*}\left(\mathbf{x}_i, i\right)+\sqrt{ {\left(\sigma_i^2-\sigma_{i-1}^2\right)} } \mathbf{z}_i, i=1,2, \cdots, N, \tag{3.13}\]

如此，我们得到了 predictor-corrector 框架中的 predictor，对于corrector，作者直接使用了 langevin dynamics。

上图展示了不同SDE下的PC（predictor-corrector）采样器的伪代码。对应的corrector 部分如下图所示：

关于不同采样器的性能对比，我们将在介绍完 PROBABILITY FLOW 预测器之后统一给出。

3.2.4 PROBABILITY FLOW

作者认为，在 score-based 模型中，对于所有前向扩散过程，存在一个对应的 deterministic（确定的） 扩散过程，该确定过程所对应的轨迹与SDE 轨迹共享不同时刻的边际概率分布 ${p_t(\mathbf{x})}_{t=0}^T$。这个确定过程满足一个常微分方程（ODE）：

\[\mathrm{d} \mathbf{x}=\left[\mathbf{f}(\mathbf{x}, t)-\frac{1}{2} g(t)^2 \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\right] \mathrm{d} t \tag{3.14}\]

上式被称为 probability flow ODE。

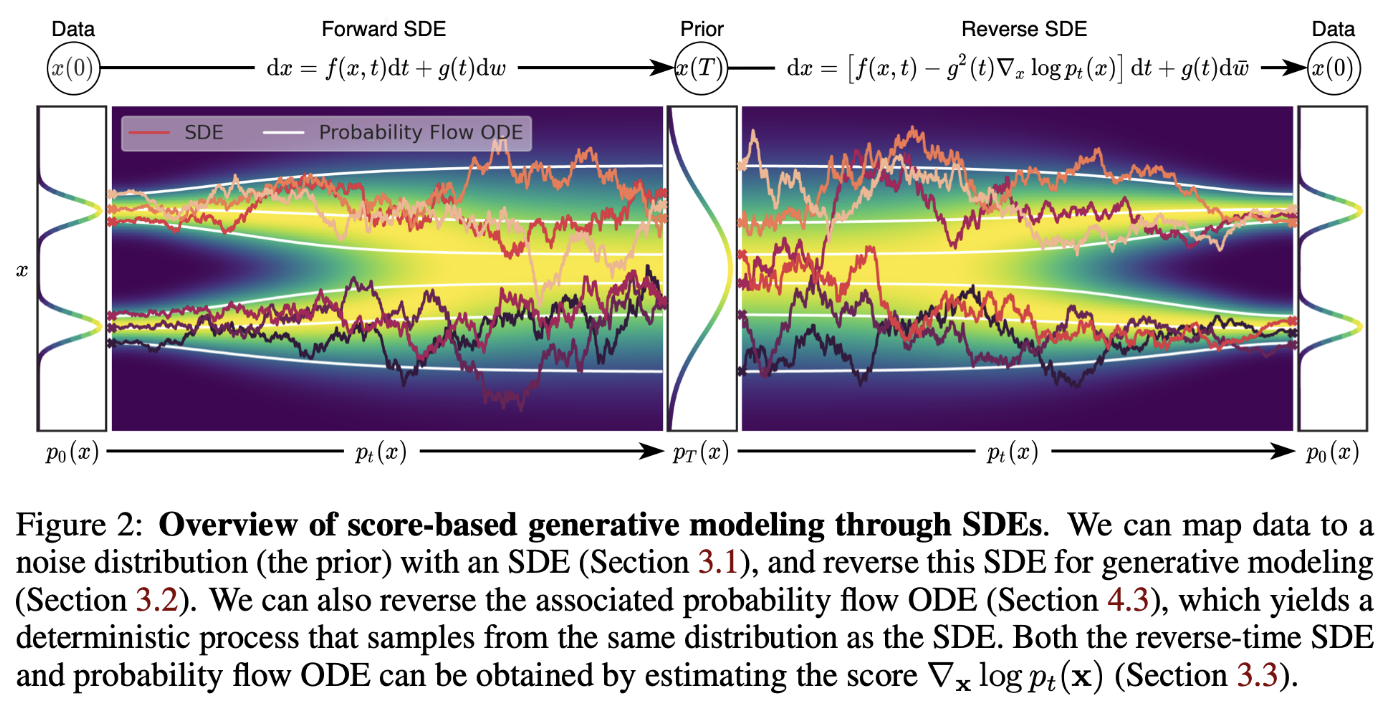
如上图所示，白色轨迹对应于probability flow ODE。probability flow ODE 是一种neural ODE。neural ODE 是神经网络与常微分方程结合的一种模型，即利用神经网络预测变量的变化率（而不是变量本身）。probability flow ODE 带来了以下几个优势：

精确的似然计算 这是neural ODEs 本身的优势，它可以允许计算任意输入样本的 精确的似然值（参考原文附D.2）。

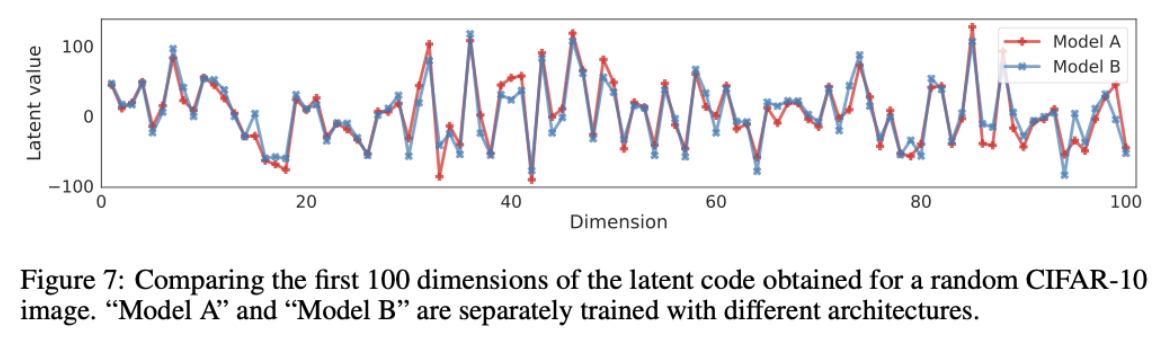
隐空间编辑 由于前向及逆向过程不包含随机性，这使得对隐空间的编辑成为可能，如插值操作（如下图所示）。

编码的唯一性 如式（25）所示，probability flow ODE 对应的前向扩散过程由 score $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$ 唯一确定。如果存在两个模型A 和 B，两者的拟合能力充足。在优化精度足够的情况下，模型A和模型B在同一个训练集上预测的 score 值将相同。此时 probability flow ODE 确定的轨迹，在A和B模型下将是一样的，最终的编码结果也是相同的。

高效采样 考虑到 probability flow ODE 是一种 neural ODEs，所以我们可以用一个 black-box ODE solver 生成样本，同时允许我们在精度和效率之间进行权衡。

上图左侧展示的是求解器精度与迭代次数的关系，纵轴表示的是求解器的计算点，当 timepoint =0，对应的是计算的终止条件，显然 precsion 越高（数值越低），需要的计算轮次越多（即需要计算score的次数——the number of score function evaluations (NFE)，表现在横轴）。上图右侧反映了不同NFE对应的生成效果。

3.2.5 不同采样器的性能对比

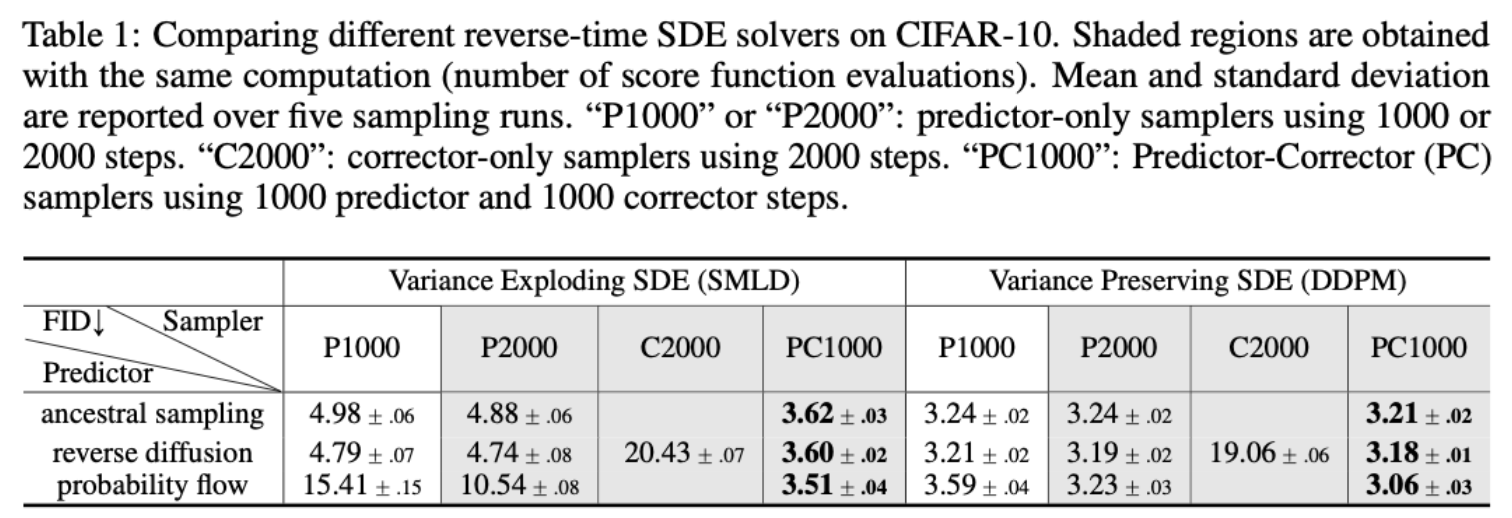
不难发现，作者提出的 reverse diffusion采样器优于之前的版本（祖先采样）。同时，组合版本的采样器（Predictor-Corrector,PC）的性能高于单独使用 Predictor 或 Corrector。

3.2.6 网络结构的提升

新的结构主要基于DDPM一文的实现[Ho]⁴，在此基础上复用了一些在GAN模型中成功的改进，具体细节参考附H.1。

3.3 相关结论

3.3.1 定量分析

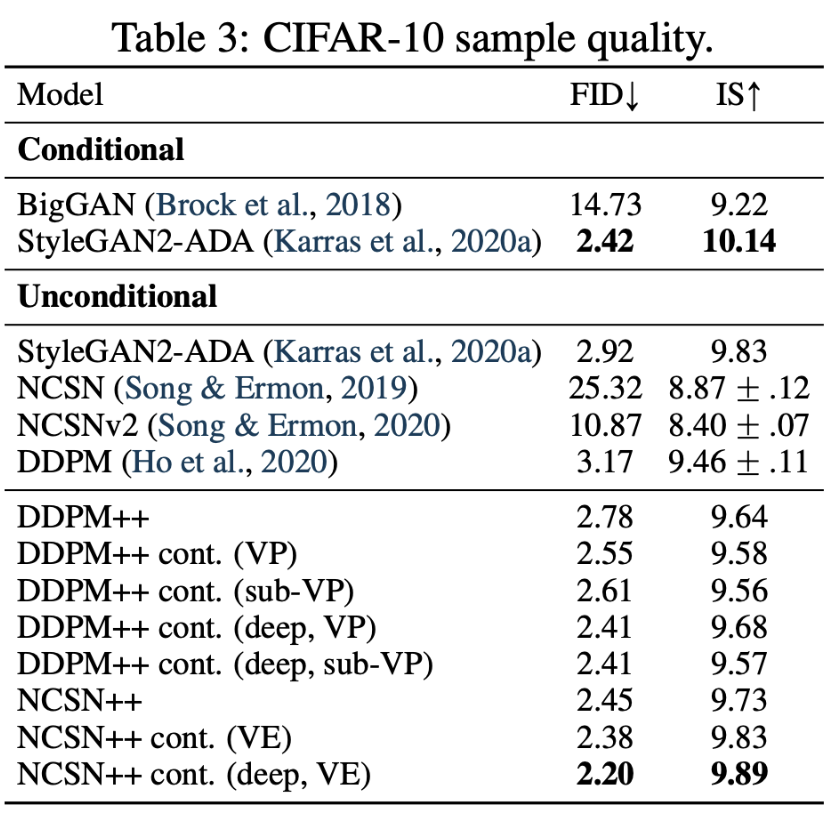
如上图所示，作者对比了改进后的方法的性能。其中 ‘++’ 表示使用了改进后的网络结构；’++ cont.’ 表示在新的结构基础上，增加了网络深度，同时使用连续设定下的优化目标（即公式（18））。图中的 ‘deep’ 是指将网络深度增加到原来的2倍。

3.3.2 原文结论

We presented a framework for score-based generative modeling based on SDEs. Our work enables a better understanding of existing approaches, new sampling algorithms, exact likelihood computation, uniquely identifiable encoding, latent code manipulation, and brings new conditional generation abilities to the family of score-based generative models. While our proposed sampling approaches improve results and enable more efficient sampling, they remain slower at sampling than GANs (Goodfellow et al., 2014) on the same datasets. Identifying ways of combining the stable learning of score-based generative models with the fast sampling of implicit models like GANs remains an important research direction. Additionally, the breadth of samplers one can use when given access to score functions introduces a number of hyper-parameters. Future work would benefit from improved methods to automatically select and tune these hyperparameters, as well as more extensive investigation on the merits and limitations of various samplers.

该研究提出了基于随机微分方程（SDEs）的分数基础生成模型框架，主要贡献包括：

1. 更好理解现有方法：为现有的score-based生成模型提供了新的理论解释。
2. 新采样算法与效率：提出了新的采样算法，尽管它们在结果和效率上有所改进，但采样速度仍逊色于生成对抗网络（GANs）。
3. 精确似然计算和潜在空间操作：提供了准确的似然计算方法，并提出了潜在编码和潜在空间操作的改进。
4. 条件生成能力：增强了基于分数的生成模型的条件生成能力。

尽管这些改进带来了更好的效果，但相比 GAN，采样速度仍较慢，且使用score函数的采样器引入了大量超参数。因此，未来的研究应聚焦于：

• 加速采样方法，将基于score的生成模型的稳定性与 GAN 等模型的快速采样结合。
• 自动选择和调优超参数，并对不同采样器的优缺点进行更深入的研究。

总体而言，未来的研究方向在于提升采样效率并优化超参数选择。

4. Consistency Models

4.1 要点概述

• 传统的score-based模型采用迭代式采样策略生成样本，时间成本高；
• 提出一致性模型（Consistency Models），可以实现噪声到样本的单步生成；
• 一致性模型可以通过两种方式训练得到：对预训练的扩散模型进行一致性蒸馏；独立训练一致性模型

4.2 深度解读

4.2.1 从 概率流 ODE（PF ODE） 开始

根据 SCORE-SDE 的介绍，概率流 ODE（PF ODE） 将原有的随机扩散过程转换成确定性的扩散过程。从样本到噪声到路径从随机性变成了确定性。换句话说，样本与噪声之间存在某个确定的映射关系。换言之，学习一个映射函数直接将噪声转换成样本成为可能。

==一致性模型试图将 PF-ODE 轨迹上的任意中间状态映射到样本本身==。既然我们可以直接将噪声映射到样本，为什么还要考虑中间状态呢？这么做有哪些好处呢，首先，使用多步迭代生图，我们可以在性能（生图质量）与成本（迭代次数）之间进行权衡；其次，这么做可以实现 zero-shot 的图像编辑（在以扩散模型为基础框架的图像编辑领域，通常是在迭代的中间步骤完成部分内容的编辑，所以多步迭代生成是前提）。

4.2.2 一致性模型的定义

给定 PF ODE 上的一条样本轨迹 \(\{\mathbf{x}_t\}_{t \in[\varepsilon, T]}\)。一致性函数 定义为 \(\boldsymbol{f}:\left(\mathbf{x}_t, t\right) \mapsto \mathbf{x}_c\)。一致性函数具备一个重要的属性 自我一致性（self-consistency）：对于同一条 PF ODE 轨迹上任意数据 $\left(\mathbf{x}_t, t\right)$，满足 \(\boldsymbol{f}\left(\mathbf{x}_t, t\right)=\boldsymbol{f}\left(\mathbf{x}_{t^{\prime}}, t^{\prime}\right)\)，\(t, t^{\prime} \in[\epsilon, T]\)。其中 $\epsilon$ 是一个接近 $0$ 的常数，\(\hat{\mathbf{x}}_{\varepsilon}\) 是样本 $\hat{\mathbf{x}}_0$ 的近似，使用前者是因为数值求解器在 $0$ 附近可能存在数值不稳定性的问题。

4.2.2.1 参数化

对任意形式的一致性函数 $f(\cdot, \cdot)$，需要满足边界条件 \(\boldsymbol{f}\left(\mathbf{x}_\epsilon, \epsilon\right)=\mathbf{x}_\epsilon\)，换句话说 \(\boldsymbol{f}(\cdot, \epsilon)\) 是一个恒等映射。为了满足该边界条件，作者提出了2种参数化形式：第一种方法是使用分段函数的形式，即：

\[\boldsymbol{f}_{\boldsymbol{\theta}}(\mathbf{x}, t)=\left\{\begin{array}{ll} \mathbf{x} & t=\epsilon \\ F_{\boldsymbol{\theta}}(\mathbf{x}, t) & t \in(\epsilon, T] \end{array} .\right. \tag{4.1}\]

第二种方法是使用跨连的方式：

\[\boldsymbol{f}_{\boldsymbol{\theta}}(\mathbf{x}, t)=c_{\text {skip }}(t) \mathbf{x}+c_{\text {out }}(t) F_{\boldsymbol{\theta}}(\mathbf{x}, t), \tag{4.2}\]

其中 $c_{\text {skip }}(t)$ 和 $c_{\text {out }}(t)$ 为关于 $t$ 的可微函数，并且满足 $c_{\text {skip }}(\epsilon)=1$ 和 $c_{\text {out }}(\epsilon)=0$。第二种参数化形式是目前主流的扩散模型形式，作者采用了第二种。

4.2.3 蒸馏法训练一致性模型

回顾PF ODE的表达式

\[\mathrm{d} \mathbf{x}_t=\left[\boldsymbol{\mu}\left(\mathbf{x}_t, t\right)-\frac{1}{2} \sigma(t)^2 \nabla \log p_t\left(\mathbf{x}_t\right)\right] \mathrm{d} t . \tag{4.3}\]

作者使用 Karras [Karras][^Karras] 中的设定：$\boldsymbol{\mu}(\mathbf{x}, t)=\mathbf{0}$，$\sigma(t)=\sqrt{2 t}$。此时的 PF ODE 为：

\[\frac{\mathrm{d} \mathbf{x}_t}{\mathrm{~d} t}=-t \boldsymbol{s}_\phi\left(\mathbf{x}_t, t\right) \tag{4.4}\]

作者称上式为 empirical PF ODE。

回到蒸馏的训练范式，在这种设定下，我们已有一个训练好的score-based 模型，换句话说，式（4.4）中的 \(s_\phi\left(\mathbf{x}_t, t\right)\) 是已知的条件。考虑将时间范围 \([\epsilon, T]\) 划分为 $N-1$ 个子区间，满足 \(t_1=\epsilon<t_2<\cdots<t_N=T\)。在实践中，作者使用 Karras [Karras][^Karras] 的设定确定区间的边界，即 \(t_i=\left(\epsilon^{1 / \rho}+i-1 / N-1\left(T^{1 / \rho}-\epsilon^{1 / \rho}\right)\right)^\rho\)，其中 $\rho=7$。当 $N$ 足够大，我们可以根据 $\mathbf{x}{t{n+1}}$ 精准地预测 $\mathbf{x}_{t_n}$—— 使用数值ODE求解器：

\[\hat{\mathbf{x}}_{t_n}^\phi:=\mathbf{x}_{t_{n+1}}+\left(t_n-t_{n+1}\right) \Phi\left(\mathbf{x}_{t_{n+1}}, t_{n+1} ; \phi\right) \tag{4.5}\]

其中 $\Phi(\cdots ; \phi)$ 表示单步 ODE 求解器应用在 empirical PF ODE 上的更新函数。举例来说，如果使用 欧拉求解器，我们有 $\Phi(\mathbf{x}, t ; \phi)=-t \boldsymbol{s}_\phi(\mathbf{x}, t)$，此时的更新步骤定义为：

\[\hat{\mathbf{x}}_{t_n}^\phi=\mathbf{x}_{t_{n+1}}-\left(t_n-t_{n+1}\right) t_{n+1} s_\phi\left(\mathbf{x}_{t_{n+1}}, t_{n+1}\right) . \tag{4.6}\]

为简单起见，作者使用单步ODE求解器。

蒸馏范式主要包含如下步骤：

• 从训练集中采样样本 $\mathbf{x} \sim p_{\text {data }}$；
• 从扰动分布 \(\mathcal{N}\left(\mathbf{x}, t_{n+1}^2 \boldsymbol{I}\right)\) 中采样含噪样本 \(\mathbf{x}_{t_{n+1}}\)；
• 使用公式（4.6）得到降噪后的样本 \(\hat{\mathbf{x}}_{t_n}^\phi\)，此时我们有 PF ODE轨迹上的两个相邻样本 \(\left(\hat{\mathbf{x}}_{t_n}^\phi, \mathbf{x}_{t_{n+1}}\right)\)；
• 接下来训练一致性蒸馏loss，最小化相邻样本对应的输出。

定义1：一致性蒸馏loss定义为：

\[\begin{aligned} & \mathcal{L}_{C D}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-} ; \boldsymbol{\phi}\right):= \\ & \quad \mathbb{E}\left[\lambda\left(t_n\right) d\left(\boldsymbol{f}_{\boldsymbol{\theta}}\left(\mathbf{x}_{t_{n+1}}, t_{n+1}\right), \boldsymbol{f}_{\boldsymbol{\theta}^{-}}\left(\hat{\mathbf{x}}_{t_n}^{\boldsymbol{\phi}}, t_n\right)\right)\right], \end{aligned} \tag{4.7}\]

式中需要关于 $\mathbf{x} \sim p_{\text {data }}$ 计算期望值，$n$ 服从均匀分布 $\mathcal{U} [1, N-1 ]$，支撑集为 ${1,2, \cdots, N-1}$。$\lambda(\cdot) \in \mathbb{R}^{+}$ 是一个大于0的加权函数，$\hat{\mathbf{x}}_{t_n}^\phi$ 由公式（4.6）决定。$\boldsymbol{\theta}^{-}$ 是参数 $\boldsymbol{\theta}$ 的滑动平均版本，作者将前者对应的函数称为“target network”，后者对应的函数称为“online network”。$d(\cdot, \cdot)$ 是一个度量函数，满足 $\forall \mathbf{x}, \mathbf{y}: d(\mathbf{x}, \mathbf{y}) \geqslant 0$，$d(\mathbf{x}, \mathbf{y})=0$ 的充要条件为 $\mathbf{x}=\mathbf{y}$。作者实验了 squared $\ell_2$ 距离，$\ell_1$ 距离 以及 Learned Perceptual Image Patch Similarity（LPIPS）[Zhang][^Zhang]。加权权重 $\lambda\left(t_n\right) \equiv 1$。

蒸馏范式的训练伪代码参考下图：

4.2.4 独立训练一致性模型

蒸馏法需要提前有一个准备好的score函数，作者提出一种单独训练一致性模型的方法，这使得一致性模型可以称为一种独立的生成建模方案。根据原文附录A 中的定理1，我们有：

\[\nabla \log p_t\left(\mathbf{x}_t\right)=-\mathbb{E}\left[\left.\frac{\mathbf{x}_t-\mathbf{x}}{t^2} \right\rvert\, \mathbf{x}_t\right], \tag{4.8}\]

其中 $\mathbf{x} \sim p_{\text {data }}$，$\mathbf{x}_t \sim \mathcal{N}\left(\mathbf{x} ; t^2 \boldsymbol{I}\right)$。换句话说，如果已知训练样本 $\mathbf{x}$ 和含噪版本 $\mathbf{x}_t$ ，我们可以使用 $-\left(\mathbf{x}_t-\mathbf{x}\right) / t^2$ 估计 $\nabla \log p_t\left(\mathbf{x}_t\right)$。作者理论证明了一致性蒸馏loss（式4.7）与一致性训练loss之间的关系：

\[\mathcal{L}_{C D}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-} ; \boldsymbol{\phi}\right)=\mathcal{L}_{C T}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-}\right)+o(\Delta t), \tag{4.9}\]

式中的一致性训练loss（consistency training objective）$\mathcal{L}_{C T}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-}\right)$ 定义为：

\[\mathbb{E}\left[\lambda\left(t_n\right) d\left(\boldsymbol{f}_{\boldsymbol{\theta}}\left(\mathbf{x}+t_{n+1} \mathbf{z}, t_{n+1}\right), \boldsymbol{f}_{\boldsymbol{\theta}^{-}}\left(\mathbf{x}+t_n \mathbf{z}, t_n\right)\right)\right], \tag{4.10}\]

式中 $\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$。进一步，如果\(\inf _N \mathcal{L}_{C D}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-} ; \boldsymbol{\phi}\right)>0\)，则 \(\mathcal{L}_{C T}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-}\right) \geqslant O(\Delta t)\)。不难发现，此时的训练目标与扩散模型的参数 $\phi$ 无关。当 \(N \rightarrow \infty\)（$\Delta t \rightarrow 0$）时，公式（4.9）的右侧将由 \(\mathcal{L}_{C T}^N\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{-}\right)\) 主导。

在训练一致性训练loss时，作者使用了一些策略。直觉上，当区间数量 $N$ 较小时，一致性蒸馏loss的“方差”更小，但“偏差”更大；当$N$ 较大时，一致性蒸馏loss的“方差”更大，但“偏差”更小。所以作者在训练过程中，逐步增加 $N$ 的大小，同时滑动平均的衰退系数也跟随 $N$ 变化。完整的训练过程参考下图的伪代码：

4.2.5 超参数选择

根据式（4.9），一致性训练与一致性蒸馏高度相关，所以在相关参数选择上，作者基于蒸馏方法进行确定。在一致性蒸馏的训练过程中，存在 度量函数 $d(\cdot, \cdot)$ ，ODE solver 以及离散步数$N$ 的超参数选择。

上图主要展示了不同的超参数配置实验，图（a）表明了使用 LPIPS 的优越性，对于ODE Solver，Heun ODE solver 是推荐的选择；对于$N$ 的选择，作者发现（图c），随着$N$ 的增加，影响逐渐减小。

对于图（d）展示的CT训练的参数敏感性实验，主要主要分析了$N$ 和 $\mu$ 的影响。根据前文的分析，自适应的调整策略可以取得最佳的效果：

\[\begin{aligned} N(k) & =\left\lceil\sqrt{\frac{k}{K}\left(\left(s_1+1\right)^2-s_0^2\right)+s_0^2}-1\right\rceil+1 \\ \mu(k) & =\exp \left(\frac{s_0 \log \mu_0}{N(k)}\right) \end{aligned} \tag{4.11}\]

上式中的 $K$ 表示总的迭代次数，$s_0$ 表示初始的离散步数，$s_1>s_0$ 表示最终的离散步数。$\mu_0>0$ 表示 EMA 的初始衰减系数。

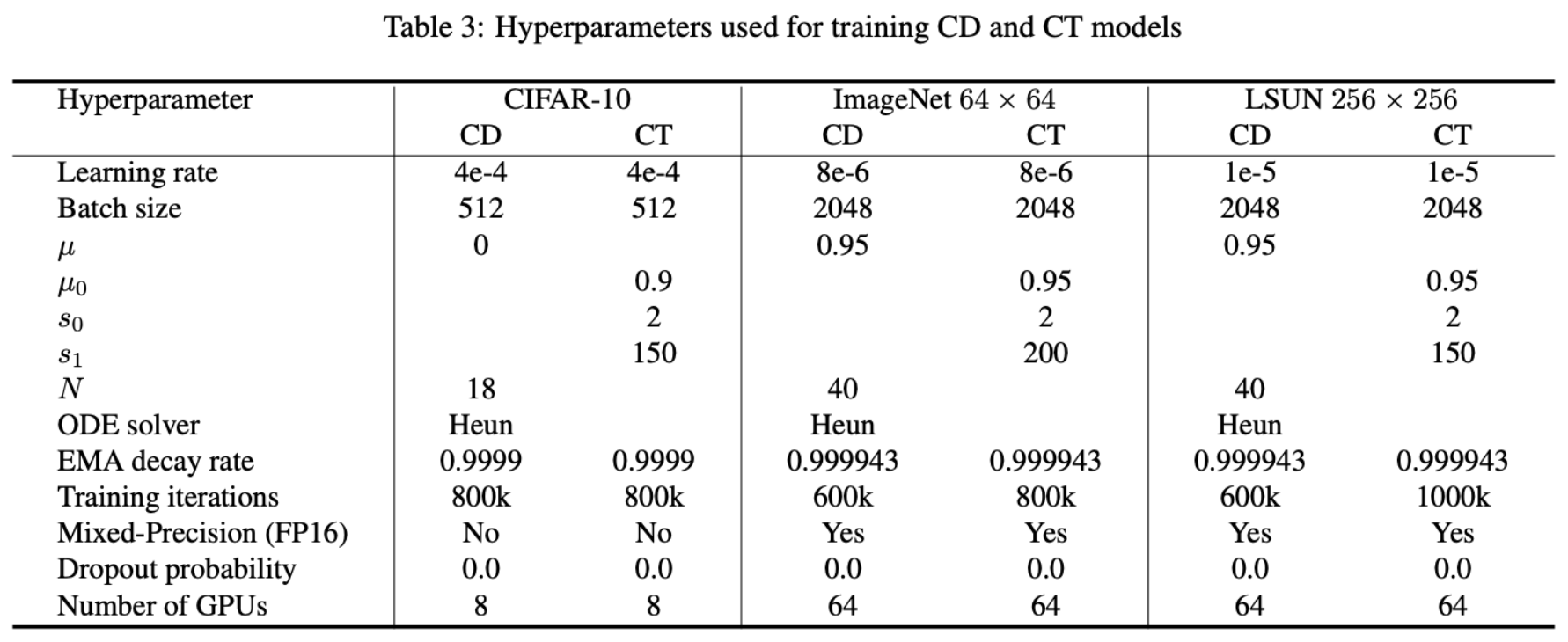
完整的超参数配置可参照下表：

4.2.6 性能对比

4.2.6.1 蒸馏方法的对比

作者将 CD 训练与progressive distillation (PD）方法[Salimans & Ho][^Salimans & Ho] 进行了对比，两种方法都不需要构造额外的数据进行训练。

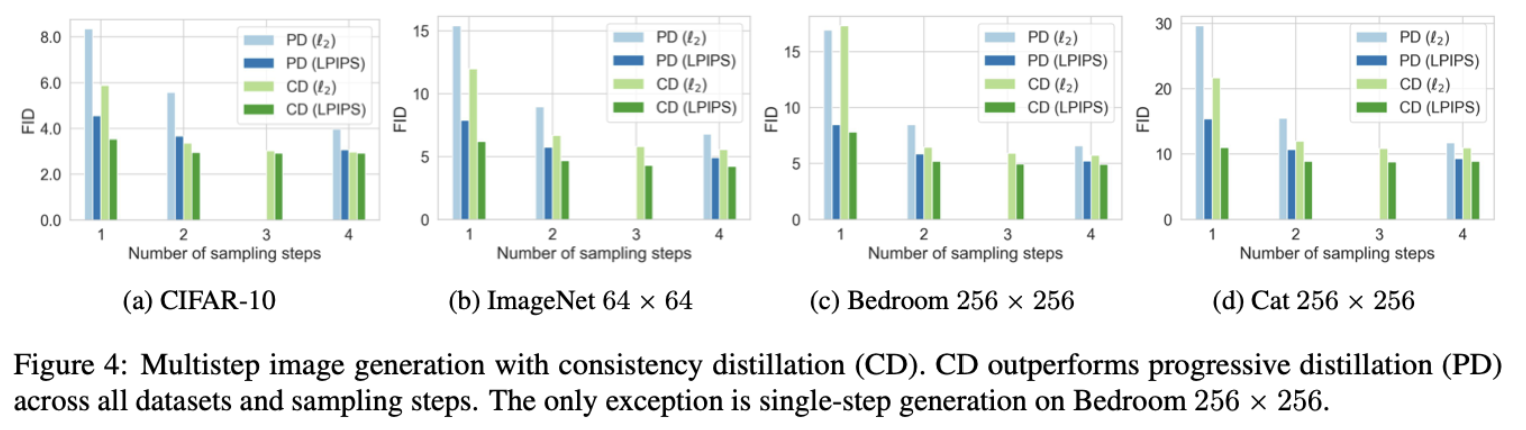
上图绿色表示CD方法，蓝色表示PD方法。显然，CD在不同数据集上一致地超过了PD法。

4.2.6.2 单步生成效果对比

作者进一步对比了CT法在单步（以及2步）生图上的优势，下图展示了在 CIFAR-10 上结果。

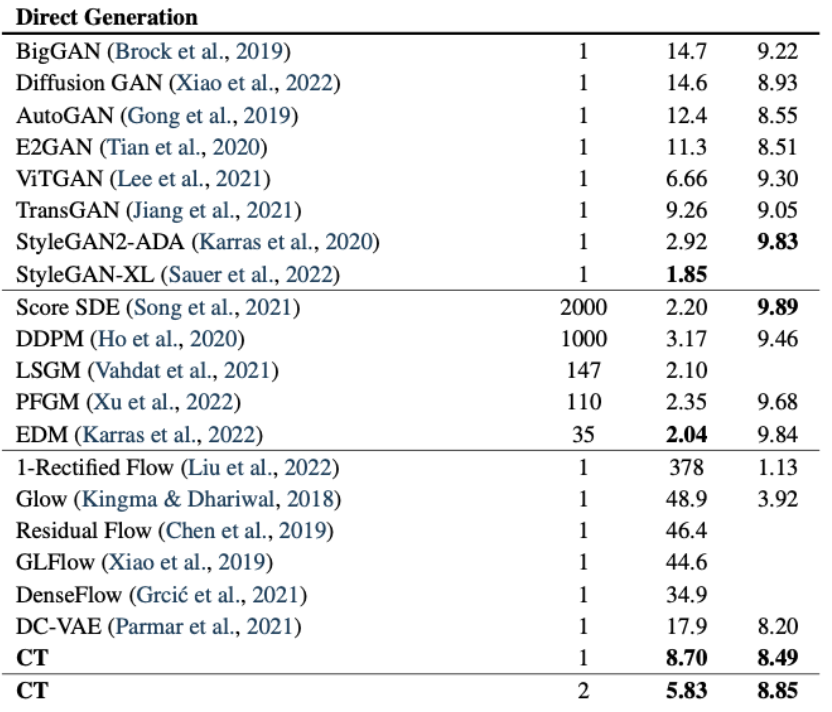
不难发现，一致性训练得到的模型的性能与最新的方案之间依然存在差距。作者在后续的工作中，改进了一致性训练的相关细节，在性能上进一步得到了提升。

4.3 结论总结

We have introduced consistency models, a type of generative models that are specifically designed to support one-step and few-step generation. We have empirically demonstrated that our consistency distillation method outshines the existing distillation techniques for diffusion models on multiple image benchmarks and small sampling iterations. Furthermore, as a standalone generative model, consistency models generate better samples than existing single-step generation models except for GANs. Similar to diffusion models, they also allow zero-shot image editing applications such as inpainting, colorization, super-resolution, denoising, interpolation, and stroke-guided image generation. In addition, consistency models share striking similarities with techniques employed in other fields, including deep Q-learning (Mnih et al., 2015) and momentum-based contrastive learning (Grill et al., 2020; He et al., 2020). This offers exciting prospects for cross-pollination of ideas and methods among these diverse fields.

作者提出了一种新的生成模型范式——一致性模型（Consistency Models）。并提出两种训练该模型的策略：一致性蒸馏和一致性训练。前者需要一个预训练的score函数，后者则可以作为一种独立的训练策略。经验表明，前者优于现有的蒸馏策略。后者在单步生成方面，优于除GAN以外的方法。除此之外，一致性模型也可以如常规的扩散模型一样，支持zero-shot的图像编辑（本博客未展示更多细节，可参考原文）。

---

以下无正文！！！

1. Y. Song, J. Sohl-Dickstein, D. P. Kingma, A. Kumar, S. Ermon, and B. Poole. Score-based generative modeling through stochastic differential equations. In Proc. ICLR, 2021. ↩ ↩² ↩³

2. P. Vincent. “A connection between score matching and denoising autoencoders”. In: Neural computation 23.7 (2011), pp. 1661–1674. ↩

3. Estimation of non-normalized statistical models by score matching. Journal of Machine Learning Research, 6(Apr):695–709, 2005. ↩

4. JonathanHo,AjayJain,andPieterAbbeel.Denoisingdiffusionprobabilisticmodels.AdvancesinNeuralInformationProcessingSystems,33,2020. ↩