6 优化

本章将系统介绍关于优化的不同方向，主要包括。。。。

• 6.1 引言
• 6.2 自动微分
  • 6.2.1 微分的函数式表达
  • 6.2.2 Differentiating chains, circuits, and programs
    • 6.2.2.1 链式组合与链式法则
    • 6.2.2.2 从链到有向无环图结构
    • 6.2.2.3 从有向无环图结构到程序
• 6.3 随机优化
  • 6.3.1 随机梯度下降
    • 6.3.1.1 如何选择步长
    • 6.3.1.2 减少梯度估计的方差
    • 6.3.1.3 预条件 SGD
  • 6.3.2 SGD用于有限和（finite-sum）目标的优化
  • 6.3.3 SGD 用于优化分布的参数
  • 6.3.4 Score 函数估计（REINFORCE）
    • 6.3.4.1 控制变量
    • 6.3.4.2 Rao-Blackwellization
  • 6.3.5 重参数化trick
    • 6.3.5.1 案例
    • 6.3.5.2 全方差
    • 6.3.5.3 “Sticking the landing” 估计器
  • 6.3.6 Gumbel softmax trick
  • 6.3.7 Stochastic computation graphs
  • 6.3.8 Straight-through estimator
• 6.4 自然梯度下降
  • 6.4.1 自然梯度的定义
  • 6.4.2 关于NGD的解释
    • 6.4.2.1 NGD 是一种信赖域优化方法
    • 6.4.2.2 NGD 是一种高斯牛顿方法
  • 6.4.3 NGD的优势
  • 6.4.4 近似自然梯度
  • 6.4.5 指数族分布的自然梯度
    • 6.4.5.1 Analytic computation for the Gaussian case
    • 6.4.5.2 Stochastic approximation for the general case
    • 6.4.5.3 能量函数的自然梯度
• 6.5 确界优化（Bound optimization）算法
  • 6.5.1 通用算法
  • 6.5.2 案例：逻辑回归
  • 6.5.3 EM算法
    • 6.5.3.1 下确界
    • 6.5.3.2 E step
    • 6.5.3.3 M step
  • 6.5.4 案例：EM 算法用于缺失数据的MVN
    • 6.5.4.1 E步骤
    • 6.5.4.2 M 步骤
    • 6.5.4.3 初始化
    • 6.5.4.4 案例
  • 6.5.5 案例：使用 Student 似然实现鲁棒线性回归
  • 6.5.6 EM的扩展
    • 6.5.6.1 变分 EM
    • 6.5.6.2 Hard EM
    • 6.5.6.3 蒙特卡洛 EM
    • 6.5.6.4 广义EM
    • 6.5.6.5 ECM 算法
    • 6.5.6.6 在线 EM
• 6.6 贝叶斯优化
  • 6.6.1 基于序列模型的优化
  • 6.6.2 代理函数
    • 6.6.2.1 高斯过程
    • 6.6.2.2 贝叶斯神经网络
    • 6.6.2.3 其他方法
  • 6.6.3 采集函数
    • 6.6.3.1 改进的概率
  • 6.6.3.2 期望提升
  • 6.6.3.3 上置信界
  • 6.6.3.4 汤普森采样
  • 6.6.3.5 熵搜索
  • 6.6.3.6 知识梯度
    • 6.6.3.7 采集函数优化
  • 6.6.4 其他问题
    • 6.6.4.1 并行（批量）查询
    • 6.6.4.2 条件参数
    • 6.6.4.3 多保真度代理模型
    • 6.6.4.4 约束优化
• 6.7 Derivative-free 优化
  • 6.7.1 局部搜索
    • 6.7.1.1 随机局部搜索
    • 6.7.1.2 Tabu search
    • 6.7.1.3 Random search
  • 6.7.2 模拟退火
  • 6.7.3 进化算法
  • 6.7.4 Estimation of distribution (EDA) 算法
  • 6.7.5 交叉熵方法
  • 6.7.6 进化策略
    • 6.7.6.1 自然进化策略
    • 6.7.6.2 协方差矩阵自适应进化策略（CMA-ES）
• 6.8 最优传输
  • 6.8.1 入门示例：两个点集之间的最优匹配
  • 6.8.2 从最优匹配到Kantorovich（坎托罗维奇）和Monge（蒙日）形式
    • 6.8.2.1 质量分割（Mass splitting）
    • 6.8.2.2 Monge形式与最优前推映射
    • 6.8.2.3 Kantorovich 形式
    • 6.8.2.4 Wasserstein distances
  • 6.8.3 最优传输的求解
    • 6.8.3.1 对偶性和损失的凹形
    • 6.8.3.2 Kantorovich-Rubinstein 对偶性与 Lipschitz 势函数
    • 6.8.3.3 蒙日映射作为凸函数梯度：布雷尼耶定理
    • 6.8.3.4 单变量与高斯分布的闭式解
    • 6.8.3.5 使用线性规划求解器精确求解
    • 6.8.3.6 利用熵正则化获得光滑性

6.1 引言

本章将讨论各种优化问题（optimization problems）。该问题可以统一定义为：

\[\boldsymbol{\theta}^* \in \underset{\boldsymbol{\theta} \in \Theta}{\operatorname{argmin}} \mathcal{L}(\boldsymbol{\theta}) \tag{6.1}\]

式中 $\mathcal{L}: \Theta \rightarrow \mathbb{R}$ 表示优化目标或损失函数，$\Theta$ 表示优化的参数空间。当然，上式隐藏了很多细节，比如优化问题是否包含额外的约束条件，优化空间是离散或是连续的，优化目标的凹凸性等等。本书上册讨论了机器学习中常见的一些优化算法。本章将讨论一些进阶的内容。更多细节可以参考其他文献 [KW19b; BV04; NW06; Ber15; Ber16]，以及一些综述文章 [BCN18; Sun+19b; PPS18; Pey20]。

6.2 自动微分

本节将讨论一个问题——对于一个 复杂 的函数，如何自动地求解函数的（偏）微分。此处的“复杂”是指任意数量的基础函数的组合，比如深度神经网络。这类任务被称为自动微分（automatic differentiation, AD 或者 autodiff）。AD 是优化和深度学习领域的基本组成部分，在不同科学和工程领域也都有应用。 [Bay+15] 主要介绍了AD在机器学习领域的应用，更多文献可以参考 [GW08][^GW08]。

6.2.1 微分的函数式表达

在探讨自动微分之前，需要回顾一下微分的数学原理。我们将使用一种特定的函数式（functional）符号来表示偏导数，而不是本书常用的表示方法——暂且称之为命名变量（named variable）符号表示法。命名变量符号表示法需要将函数的参数与某个变量绑定。例如，给定函数 $f: \mathbb{R}^2 \rightarrow \mathbb{R}$，在点 $\boldsymbol{a}=\left(a_1, a_2\right)$ 处，$f$ 关于第一个标量参数的偏导数为：

\[\left.\frac{\partial f}{\partial x_1}\right|_{\boldsymbol{x}=\boldsymbol{a}} \tag{6.2}\]

这种表示方法并非完全自包含，它涉及另一个变量 $\boldsymbol{x}=\left(x_1, x_2\right)$，该变量可能是隐含的或从上下文中推断出来的，暗示函数 $f$ 的参数。另一种表达方式是：

\[\frac{\partial}{\partial a_1} f\left(a_1, a_2\right) \tag{6.3}\]

在这种表示法中，$a_1$ 既充当了命令变量的角色，也指代某个具体的求值点。随着被组合的函数数量增加，每个函数可能接受多个参数，处理这些参数的命名方式会变得越来越复杂。

函数式符号表示法则将导数定义为 作用于函数的运算符。如果某个函数包含多个参数，则通过位置而非名称来区分它们，从而避免引入辅助的命名变量。接下来的某些定义借鉴了斯皮瓦克（Spivak）的《流形上的微积分》（Calculus on Manifolds）[Spi71]以及萨斯曼（Sussman）和威斯多姆（Wisdom）的《函数微分几何》（Functional Differential Geometry）[SW13]中的内容，这些内容通常在微分学和几何学中更为常见。对于本节涉及到的部分，建议参考这些书籍以获得更正式的处理方式和更数学化的视角。

除了表示方法之外，我们还将依赖一些基本的多变量微积分概念。其中包括（偏）导数、函数在某求值点的微分或雅可比矩阵（Jacobian），函数在某求值点的局部线性近似等。我们将集中讨论空间维度有限的情形，并用 ${\boldsymbol{e}_1, \ldots, \boldsymbol{e}_n}$ 表示空间 $\mathbb{R}^n$ 中的标准基。

线性和多层线性函数 令 $F: \mathbb{R}^n \multimap \mathbb{R}^m$ 表示线性函数 $F: \mathbb{R}^n \rightarrow \mathbb{R}^m$，并用 $F[\boldsymbol{x}]$ 表示函数作用于 $\boldsymbol{x} \in \mathbb{R}^n$。回想一下，线性映射实际上对应于空间 $\mathbb{R}^{m \times n}$ 中的一个矩阵——列向量分别为 $F\left[\boldsymbol{e}_1\right], \ldots, F\left[\boldsymbol{e}_n\right]$；函数视角和矩阵视角的两种解释都是有用的。巧合的是，函数组合和矩阵乘法在表达方式上看起来是相似的：两个线性映射 $F$ 和 $G$ 的组合可以写成 $F \circ G$，或者稍微放宽符号的严格定义——考虑使用矩阵 $F G$。每个线性映射 $F: \mathbb{R}^n \multimap \mathbb{R}^m$ 都存在一个转置 $F: \mathbb{R}^m \multimap \mathbb{R}^n$，这是另一个线性映射，可以通过转置相应的矩阵来实现。

函数视角和矩阵视角实际上是运动的相对性，前者是 x 的变换，后者是空间（基）的变换。

重复使用线性函数中的符号：

\[T: \underbrace{\mathbb{R}^n \multimap \cdots \multimap \mathbb{R}^n}_{k \text { times }} \multimap \mathbb{R}^m \tag{6.4}\]

上式表示一个多层线性映射，或者更准确的叫 $k-$线性映射：

\[T: \underbrace{\mathbb{R}^n \times \cdots \times \mathbb{R}^n}_{k \text { times }} \rightarrow \mathbb{R}^m \tag{6.5}\]

上式表示一个数组（或者张量）$\mathbb{R}^{m \times n \times \cdots \times n}$。我们使用 $T\left[\boldsymbol{x}_1, \ldots, \boldsymbol{x}_k\right] \in \mathbb{R}^m$ 表示将上述的 $k-$线性映射依次作用于向量 $\boldsymbol{x}_1, \ldots, \boldsymbol{x}_k \in \mathbb{R}^n$。

导数运算符. 对于开集 $U \subset \mathbb{R}^n$ 和可微函数 $f: U \rightarrow \mathbb{R}^m$，令其导函数（derivative function）为：

\[\partial f: U \rightarrow\left(\mathbb{R}^n \multimap \mathbb{R}^m\right) \tag{6.6}\]

或者等价地表示为 $\partial f: U \rightarrow \mathbb{R}^{m \times n}$。此函数将点 $\boldsymbol{x} \in U$ 映射到函数在 $\boldsymbol{x}$ 处的雅可比矩阵。符号 $\partial$ 表示导数运算符（derivative operator），这是一个将函数映射到其导函数的函数。当 $m = 1$ 时，映射 $\partial f(\boldsymbol{x})$ 在任意 $\boldsymbol{x} \in U$ 处的结果等价于标准梯度 $\nabla f(\boldsymbol{x})$。事实上，nabla 符号 $\nabla$ 有时也被描述为一个运算符，因此 $\nabla f$ 也是一个函数。当 $n = m = 1$ 时，雅可比矩阵退化为标量，此时 $\partial f$ 即为常见的导数 $f^{\prime}$。

在表达式 $\partial f(\boldsymbol{x})[\boldsymbol{v}]$ 中，称 $\boldsymbol{x}$ 为雅可比矩阵的线性化点（linearization point），而称 $\boldsymbol{v}$ 为扰动（perturbation）。我们将映射：

\[(\boldsymbol{x}, \boldsymbol{v}) \mapsto \partial f(\boldsymbol{x})[\boldsymbol{v}] \tag{6.7}\]

称为关于线性化点 $\boldsymbol{x} \in U$ 和输入扰动 $\boldsymbol{v} \in \mathbb{R}^n$ 的雅可比-向量积（Jacobian-vector product，JVP）。类似地，我们称其转置：

\[(\boldsymbol{x}, \boldsymbol{u}) \mapsto \partial f(\boldsymbol{x})^{\mathrm{T}}[\boldsymbol{u}] \tag{6.8}\]

为关于线性化点 $\boldsymbol{x} \in U$ 和输出扰动 $\boldsymbol{u} \in \mathbb{R}^m$ 的向量-雅可比积（Vector-Jacobian Product, VJP）。

正如我们接下来所展示的那样，使用映射而非矩阵的表示方法，有助于我们递归地定义高阶导数。这也暗示了雅可比矩阵在代码中常规的实现方式。当我们在程序中考虑为固定的 $\boldsymbol{x}$ 编写 $\partial f(\boldsymbol{x})$ 时，通常将其实现为一个执行雅可比矩阵乘法的函数，即 $\boldsymbol{v} \mapsto \partial f(\boldsymbol{x})[\boldsymbol{v}]$，而不是显式地将其表示为内存中的数值矩阵。更进一步来说，我们通常将 $\partial f$ 实现为一次完整的雅可比-向量积（JVP）——针对任意线性化点$\boldsymbol{x}$和扰动$\boldsymbol{v}$。举一个标量的简单例子，考虑余弦函数：

\[(x, v) \mapsto \partial \cos (x) v=-v \sin (x) \tag{6.9}\]

如果我们在代码中直接实现这个逻辑（比如某个数学公式或优化策略），就可以在某些情况下（比如变量 $v=0$ 时）避免计算 $\sin (x)$，从而提高计算效率。

高阶导数. 假设上述函数 $f$ 在其定义域 $U \subset \mathbb{R}^n$ 上任意阶可微。为了计算更高阶的导数，符号上可以写作：

\[\partial^2 f: U \rightarrow\left(\mathbb{R}^n \multimap \mathbb{R}^n \multimap \mathbb{R}^m\right) \tag{6.10}\]

其中，$\partial^2 f(\boldsymbol{x})$ 表示双线性映射——即所有的二阶偏导数。在命名变量符号表示法中，可以使用 $\frac{\partial f(\boldsymbol{x})}{\partial x_i \partial x_j}$ 来指代 $\partial^2 f(\boldsymbol{x})\left[\boldsymbol{e}_i, \boldsymbol{e}_j\right]$。

二阶导函数 $\partial^2 f$ 可以看作是应用了两次导数算子的结果。也就是说，可以合理地认为 $\partial^2=\partial \circ \partial$。这一观察可以递归地扩展到任意高阶导数。对于 $k \geq 1$：

\[\partial^k f: U \rightarrow(\underbrace{\mathbb{R}^n \multimap \ldots \multimap \mathbb{R}^n}_{k \text { times }} \multimap \mathbb{R}^m) \tag{6.11}\]

$\partial^k f(\boldsymbol{x})$ 是一个 $k-$线性映射。

当 $m = 1$ 时，映射 $\partial^2 f(\boldsymbol{x})$ 对应函数在任意 $\boldsymbol{x} \in U$ 处的 Hessian 矩阵。尽管雅可比矩阵和 Hessian 矩阵足以理解许多机器学习技术，但任意高阶导数也并不少见（例如，[Kel+20]）。举个例子，在函数的泰勒级数展开式中，我们可以用导数算子将其表示为：

\[f(\boldsymbol{x}+\boldsymbol{v}) \approx f(\boldsymbol{x})+\partial f(\boldsymbol{x})[\boldsymbol{v}]+\frac{1}{2!} \partial^2 f(\boldsymbol{x})[\boldsymbol{v}, \boldsymbol{v}]+\cdots+\frac{1}{k!} \partial^k f(\boldsymbol{x})[\boldsymbol{v}, \ldots, \boldsymbol{v}] \tag{6.12}\]

多个输入. 现在考虑函数包含多个输入：

\[g: U \times V \rightarrow \mathbb{R}^m \tag{6.13}\]

其中 $U \subset \mathbb{R}^{n_1}$， $V \subset \mathbb{R}^{n_2}$。实际上，像 $U \times V$ 这样的积域主要用于表明函数输入的不同组成部分，它与 $\mathbb{R}^{n_1+n_2}$ 的子集同构，后者对应于一个单输入函数。接下来将介绍 $g$ 的导函数，我们将在两种视角之间自由切换。多输入的情况通常出现在计算图和代码程序的上下文中：代码中的许多函数被编写为接受多个参数，许多基本操作（例如加法 +）也是如此。

对于多输入函数，我们可以用 $\partial_i g$ 表示函数关于第 $i$ 个参数的导函数：

\[\begin{align} & \partial_1 g: \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \rightarrow\left(\mathbb{R}^{n_1} \multimap \mathbb{R}^m\right), \text { and } \tag{6.14}\\ & \partial_2 g: \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \rightarrow\left(\mathbb{R}^{n_2} \multimap \mathbb{R}^m\right) \tag{6.15} \end{align}\]

在矩阵视角下，函数 $\partial_1 g$ 将点对 $\boldsymbol{x} \in \mathbb{R}^{n_1}$ 和 $\boldsymbol{y} \in \mathbb{R}^{n_2}$ 映射到函数 $g$ 关于第一个参数的所有偏导数矩阵，并在 $(\boldsymbol{x}, \boldsymbol{y})$ 处求值。我们用不带下标的 $\partial g$ 简单地表示 $\partial_1 g$ 和 $\partial_2 g$ 的拼接：

\[\partial g: \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \rightarrow\left(\mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \multimap \mathbb{R}^m\right) \tag{6.16}\]

对于每一个线性化点 $(\boldsymbol{x}, \boldsymbol{y}) \in U \times V$ 和扰动 $\dot{\boldsymbol{x}} \in \mathbb{R}^{n_1}, \dot{\boldsymbol{y}} \in \mathbb{R}^{n_2}$，我们有：

\[\partial g(\boldsymbol{x}, \boldsymbol{y})[\dot{\boldsymbol{x}}, \dot{\boldsymbol{y}}]=\partial_1 g(\boldsymbol{x}, \boldsymbol{y})[\dot{\boldsymbol{x}}]+\partial_2 g(\boldsymbol{x}, \boldsymbol{y})[\dot{\boldsymbol{y}}] . \tag{6.17}\]

另一种矩阵视角下的写法：

\[\partial g(\boldsymbol{x}, \boldsymbol{y})=\left(\partial_1 g(\boldsymbol{x}, \boldsymbol{y}) \quad \partial_2 g(\boldsymbol{x}, \boldsymbol{y})\right) \tag{6.18}\]

这一约定将简化下面介绍的链式法则。当 $n_1=n_2=m=1$ 时，两个子矩阵都是标量， $\partial g_1(x, y)$ 恢复以命名变量符号表示法写成的偏导数：

\[\frac{\partial}{\partial x} g(x, y). \tag{6.19}\]

然而，表达式 $\partial g_1$ 本身（作为一个函数）是具有意义的，而表达式 $\frac{\partial g}{\partial x}$ 在没有额外上下文的情况下可能会产生歧义。再次通过算子组合，我们可以写出高阶导数。例如，$\partial_2 \partial_1 g(\boldsymbol{x}, \boldsymbol{y}) \in \mathbb{R}^{m \times n_1 \times n_2}$，如果 $m = 1$， $g$ 在 $(\boldsymbol{x}, \boldsymbol{y})$ 处的 Hessian 矩阵定义为：

\[\left(\begin{array}{ll} \partial_1 \partial_1 g(\boldsymbol{x}, \boldsymbol{y}) & \partial_1 \partial_2 g(\boldsymbol{x}, \boldsymbol{y}) \\ \partial_2 \partial_1 g(\boldsymbol{x}, \boldsymbol{y}) & \partial_2 \partial_2 g(\boldsymbol{x}, \boldsymbol{y}) \end{array}\right) \tag{6.20}\]

复合函数与扇出 对于 $h: \mathbb{R}^n \rightarrow \mathbb{R}^p$ 和 $g: \mathbb{R}^p \rightarrow \mathbb{R}^m$，有复合函数 $f=g \circ h$，链式法则指出：

\[\partial f(\boldsymbol{x})=\partial g(h(\boldsymbol{x})) \circ \partial h(\boldsymbol{x}) \text { for all } \boldsymbol{x} \in \mathbb{R}^n \tag{6.21}\]

这与多参数函数的符号表示法有何关联呢？首先，它可能引导我们考虑具有扇出的表达式——一个输入被多个子表达式消费使用。 例如，假设有两个函数 $a: \mathbb{R}^n \rightarrow \mathbb{R}^{m_2}$ 和 $b: \mathbb{R}^n \rightarrow \mathbb{R}^{m_2}$，并且对于某个函数 $g$，有：

\[f(\boldsymbol{x})=g(a(\boldsymbol{x}), b(\boldsymbol{x})) \tag{6.22}\]

令 $h(\boldsymbol{x})=(a(\boldsymbol{x}), b(\boldsymbol{x}))$ ，则 $f(\boldsymbol{x})=g(h(\boldsymbol{x}))$，根据公式（6.16）和（6.21），我们有：

\[\begin{align} \partial f(\boldsymbol{x}) & =\partial g(h(\boldsymbol{x})) \circ \partial h(\boldsymbol{x}) \tag{6.23} \\ & =\partial_1 g(a(\boldsymbol{x}), b(\boldsymbol{x})) \circ \partial a(\boldsymbol{x})+\partial_2 g(a(\boldsymbol{x}), b(\boldsymbol{x})) \circ \partial b(\boldsymbol{x}) \tag{6.24} \end{align}\]

注意，这里的 + 是逐点计算的。此外，如果改为：

\[f(\boldsymbol{x}, \boldsymbol{y})=g(a(\boldsymbol{x}), b(\boldsymbol{y})) \tag{6.25}\]

换句话说，如果存在多个参数但没有扇出，那么：

\[\begin{align} & \partial_1 f(\boldsymbol{x}, \boldsymbol{y})=\partial_1 g(a(\boldsymbol{x}), b(\boldsymbol{y})) \circ \partial a(\boldsymbol{x}), \text { and } \tag{6.26} \\ & \partial_2 f(\boldsymbol{x}, \boldsymbol{y})=\partial_2 g(a(\boldsymbol{x}), b(\boldsymbol{y})) \circ \partial b(\boldsymbol{y}) \tag{6.27} \end{align}\]

导数的复合与扇出规则使我们能够将复杂的导数计算分解为更简单的部分。这正是自动微分技术在处理现代机器学习和数值编程中出现的复杂数值计算时所依赖的。

6.2.2 Differentiating chains, circuits, and programs

自动微分的目的是计算作为输入提供的任意函数的导数。已知函数 $f: U \subset \mathbb{R}^n \rightarrow \mathbb{R}^m$ 以及线性化点 $\boldsymbol{x} \in U$，自动微分（AD）能够计算出以下两者之一：

• 对于输入扰动 $\boldsymbol{v} \in \mathbb{R}^n$，自动微分可以计算雅可比-向量积（JVP）$\partial f(\boldsymbol{x})[v]$；

• 对于输出扰动 $\boldsymbol{u} \in \mathbb{R}^m$，计算向量-雅可比积（VJP）$\partial f(\boldsymbol{x})^{\top}[u]$。

换言之，雅可比向量积（JVP）和向量雅可比积（VJP）覆盖了自动微分（AD）的两项核心任务。

决定将哪些函数 $f$ 作为输入处理以及如何表示它们，或许是整个体系中最关键的环节。我们应该在什么样的函数语言上进行操作？所谓语言，是指通过组合一组基本原语操作来描述函数的形式化方法。对于原语，可以考虑各种可微数组操作（逐元素算术、归约、收缩、索引与切片、连接等），但我们将主要把原语及其导数视为既定要素，并专注于其组合方式的复杂程度。随着语言表达能力的增强，自动微分也变得越来越具有挑战性。有鉴于此，我们将分阶段引入这一技术。

6.2.2.1 链式组合与链式法则

首先，仅考虑由基本操作链式组合（chain compositions）而成的函数。链式结构是一类便于处理的函数表示方式，因为根据链式法则，导数将沿着相同的结构进行分解。

作为一个简单的例子，考虑函数 $f: \mathbb{R}^n \rightarrow \mathbb{R}^m$，它由三个操作依次组成：

\[f=c \circ b \circ a \tag{6.28}\]

使用链式法则，导数为：

\[\partial f(\boldsymbol{x})=\partial c(b(a(\boldsymbol{x}))) \circ \partial b(a(\boldsymbol{x})) \circ \partial a(\boldsymbol{x}) \tag{6.29}\]

现在考虑输入扰动 $\boldsymbol{v} \in \mathbb{R}^n$ 下的 JVP：

\[\partial f(\boldsymbol{x})[\boldsymbol{v}]=\partial c(b(a(\boldsymbol{x})))[\partial b(a(\boldsymbol{x}))[\partial a(\boldsymbol{x})[\boldsymbol{v}]]] \tag{6.30}\]

此表达式的括号强调了从右到左的求值顺序，这与前向模式自动微分（forwardmode automatic differentiation）相对应。也就是说，为了执行这个雅可比向量积（JVP），计算原始链的前缀是有意义的：

\[\boldsymbol{x}, a(\boldsymbol{x}), b(a(\boldsymbol{x})) \tag{6.31}\]

同时计算部分雅可比向量积（JVP），因为每个部分随后都会立即用作后续的线性化点，具体如下：

\[\partial a\underline{(\boldsymbol{x})}, \partial b \underline{(a(\boldsymbol{x}))}, \partial c\underline{(b(a(\boldsymbol{x})))} \tag{6.32}\]

将这一思想扩展到任意链式组合，便得到了算法6.1。

相比之下，我们可以转置方程（6.29）来考虑输出扰动 $\boldsymbol{u} \in \mathbb{R}^m$ 下的向量雅可比积（VJP）：

\[\partial f(\boldsymbol{x})^{\mathrm{T}}[\boldsymbol{u}]=\partial a(\boldsymbol{x})^{\mathrm{\top}}\left[\partial b(a(\boldsymbol{x}))^{\mathrm{\top}}\left[\partial c(b(a(\boldsymbol{x})))^{\mathrm{T}}[\boldsymbol{u}]\right]\right] \tag{6.33}\]

转置操作反转了雅可比映射，现在括号内的求值对应于反向模式自动微分（reverse-mode automatic differentiation）。为了执行这个向量雅可比积（VJP），我们可以首先计算原始链的前缀$\boldsymbol{x}$、$a(\boldsymbol{x})$ 和 $b(a(\boldsymbol{x}))$，然后将它们反向读取作为连续的线性化点：

\[\partial c \underline{(b(a(\boldsymbol{x})))^{\top}}, \partial b \underline{(a(\boldsymbol{x}))^{\top}}, \partial a \underline{(\boldsymbol{x})^{\top}} \tag{6.34}\]

将这一思想扩展到任意链式组合，便得到了算法6.2。

尽管链式复合结构具有高度特异性，但它们已经能够描述某些深度学习模型，例如多层感知机（前提是将矩阵乘法视为原语操作），正如本书前作[Mur22, 第13章]所阐述的。

当输出为标量值时（此类情况在深度学习中极为常见，例如输出为损失函数时），反向模式自动微分的计算速度优于前向模式。然而，反向模式自动微分需在反向传播前存储所有计算链的中间结果，因此其内存消耗高于前向模式。针对特定场景存在缓解内存压力的方法，例如当链式操作均为可逆运算时[MDA15; Gom+17; KKL20]。此外，也可通过舍弃部分中间结果并在需要时重新计算的策略，实现内存与计算资源的权衡。

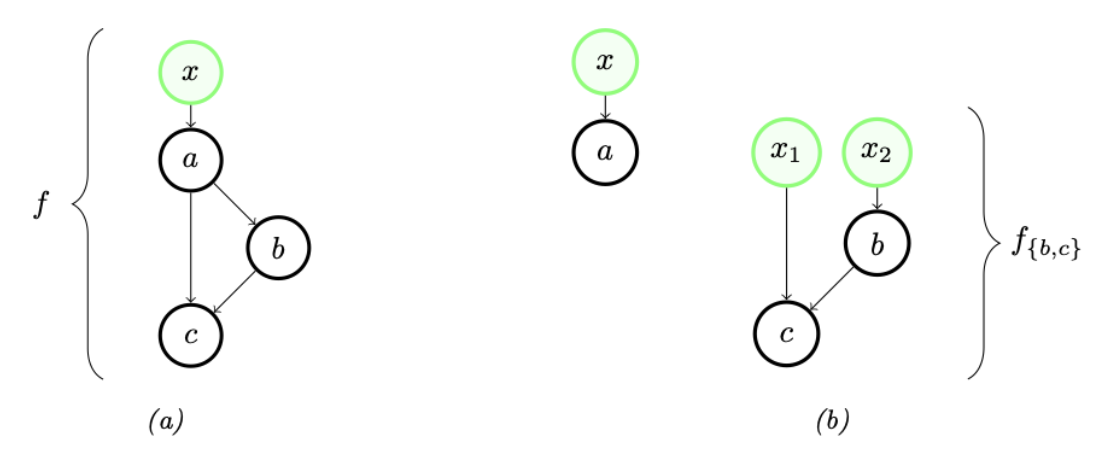
6.2.2.2 从链到有向无环图结构

当原语操作能够接受多个输入时，我们可以很自然地将链式结构扩展为circuits——一种基于原语操作的有向无环图，有时也被称为计算图。为了给本节的讨论奠定基础，我们将区分circuits中的两种节点：(1) 输入节点，代表函数的参数；(2) 原语节点，每个节点都标有一个原语操作。我们假设输入节点没有入边，且（在不失一般性的前提下）每个输入节点恰好有一条出边，同时circuits只有一个汇节点。circuits的整体功能是从输入节点到汇节点的操作组合，其中每个操作的输出根据其出边作为其他操作的输入。

第6.2.2.1节中自动微分能够实现，关键在于导数凭借 aptly-named 链式法则沿着链式结构分解。当从链式结构转向有向无环图时，我们是否需要某种“图规则”来沿着circuits结构分解计算？circuits引入了两个新特性：扇入与扇出。用图形术语来说，扇入指的是一个节点有多个入边，扇出则指一个节点有多个出边。

这些特性在函数意义上意味着什么？扇入发生在原语操作接受多个参数时。我们在第6.2.1节中观察到，多个参数可以被视为一个整体，并讨论了链式法则如何随之应用。扇出则需要稍加注意，特别是对于反向模式微分。

通过一个小例子可以说明其中的要点。考虑图6.1a中的circuits：操作 $a$ 在拓扑顺序上先于 $b$ 和 $c$，且各有出边指向这两个操作。我们可以将 $a$ 从 ${b, c}$ 中分离，生成两个新circuits（如图6.1b所示）。第一个对应 $a$ 本身，第二个对应剩余的计算部分，其表达式为：

\[f_{\{b, c\}}\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)=c\left(\boldsymbol{x}_1, b\left(\boldsymbol{x}_2\right)\right) \tag{6.35}\]

我们可以借助一个dup函数，从 $a$ 和 $f_{{b,c}}$中恢复出完整的函数 $f$，其中dup函数定义为：

\[\operatorname{dup}(\boldsymbol{x})=(\boldsymbol{x}, \boldsymbol{x}) \equiv\binom{I}{I} \boldsymbol{x} \tag{6.36}\]

所以 $f$ 可以写成一个链式组合：

\[f=f_{\{b, c\}} \circ \operatorname{dup} \circ a . \tag{6.37}\]

$f_{{b, c}}$ 中不包含扇出，而方程（6.25）的组合规则告诉我们其导数可以通过$b$、$c$及其导数来表示，这些都依赖于链式法则。同时，对方程（6.37）使用链式法则：

\[\begin{align} \partial f(\boldsymbol{x}) & =\partial f_{\{b, c\}}(\operatorname{dup}(a(\boldsymbol{x}))) \circ \partial \operatorname{dup}(a(\boldsymbol{x})) \circ \partial a(\boldsymbol{x}) \tag{6.38} \\ & =\partial f_{\{b, c\}}(a(\boldsymbol{x}), a(\boldsymbol{x})) \circ\binom{I}{I} \circ \partial a(\boldsymbol{x}) . \tag{6.39} \end{align}\]

上述表达式建议通过从右到左的求值来计算 $f$ 的雅可比向量积（JVP）。它与方程（6.30）所建议的JVP计算类似，但在中间多了一个由dup的雅可比矩阵引起的复制操作 $\left(\begin{array}{ll}I & I\end{array}\right)^{\top}$。

转置 $f$ 在 $\boldsymbol{x}$ 处的导数：

\[\partial f(\boldsymbol{x})^{\top}=\partial a(\boldsymbol{x})^{\top} \circ\left(\begin{array}{ll} I & I \end{array}\right) \circ \partial f_{\{b, c\}}(a(\boldsymbol{x}), a(\boldsymbol{x}))^{\top} . \tag{6.40}\]

考虑到从右到左的求值，这也与方程（6.33）所建议的VJP计算类似，但在中间多了一个由dup的转置雅可比矩阵引起的求和操作 $\left(\begin{array}{ll}I & I\end{array}\right)$。在这个小例子中使用dup的教训是，更一般地说，为了在反向模式AD中处理扇出，我们可以按照拓扑顺序处理操作——首先向前，然后反向——然后沿着多个出边对部分VJP进行求和。

算法6.3和6.4完整描述了circuits上的前向和反向模式微分。为了简洁起见，它们假设整个circuits函数只有一个参数。节点被索引为 $1, \ldots, T$。第一个是输入节点，其余的 $T - 1$个节点由其操作 $f_2, \ldots, f_T$ 标记。我们将 $f_1$ 视为恒等函数。对于每个 $t$，如果 $f_t$ 接受 $k$ 个参数，则令 $\mathrm{Pa}(t)$ 为其父节点的 $k$ 个索引的有序列表（可能包含重复项，由于扇出），并令 $\operatorname{Ch}(t)$ 为其子节点的索引（同样可能重复）。算法6.4采用了一些额外的约定：$f_T$是恒等函数，节点 $T$ 的唯一父节点是 $T - 1$，节点1的子节点是节点2。

扇出是图的一个特性，但可以说不是函数的一个本质特性。人们总是可以通过复制节点来从circuits中移除所有扇出。我们对扇出的兴趣正是为了避免这种情况，从而允许有效的表示，进而在算法6.3和6.4中实现高效的内存使用。

多年来，circuits上的反向模式AD以各种名称和形式出现。该算法正是神经网络中的反向传播算法，这一术语在20世纪80年代引入[RHW86b; RHW86a]，并且在控制理论和灵敏度分析的背景下也独立出现，正如Goodfellow、Bengio和Courville在历史笔记中所总结的那样[GBC16, 第6.6节]。

6.2.2.3 从有向无环图结构到程序

图对于引入自动微分（AD）算法非常有用，并且它们可能与神经网络应用很好地契合。但计算机科学家已经花费了数十年时间来形式化和研究各种“用于组合表达函数的语言”。简而言之，这就是编程语言的用途！我们能否自动微分用Python、Haskell或某种lambda演算变体等表达的数值函数？这些提供了更广泛且直观上更具表现力的方式来描述输入函数。

在前几节中，随着我们允许更复杂的图结构，我们的AD方法变得更加复杂。当我们引入编程语言中的语法结构时，也会发生类似的情况。我们如何调整AD以处理具有循环、条件语句和递归调用的语言？并行编程结构又如何？对于这些问题，我们今天有部分答案，尽管它们需要更深入地探讨语言细节，如类型系统和实现问题[Yu+18; Inn20; Pas+21b]。

由于第6.2.2.2节，我们已经知道如何处理的一个示例语言结构是标准的let表达式。在具有名称或变量绑定机制的语言中，同一变量的多次出现类似于circuits中的扇出。图6.1a对应于一个函数 $f$，我们可以用函数式语言将其写为：

f(x) =
	let ax = ax
		in c(ax, b(ax))

其中 $\rm{ax}$ 在绑定后确实出现了两次。

理解语言能力与自动可微性之间的相互作用是计算机科学研究的持续主题[PS08a; AP19; Vyt+19; BMP19; MP21]。与此同时，函数式语言在最近的AD系统中已被证明非常有效，无论是广泛使用的还是实验性的系统。诸如JAX、Dex等系统围绕纯函数式编程模型设计，并在内部依赖函数式程序表示进行微分[Mac+15; BPS16; Sha+19; FJL18; Bra+18; Mac+19; Dex; Fro+21; Pas+21a]。

6.3 随机优化

本节将讨论随机目标的优化问题：

\[\mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{q_\boldsymbol{\theta}(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})] \tag{6.41}\]

其中 $\boldsymbol{\theta}$ 表示待优化的参数， $\boldsymbol{z}$ 表示随机变量——如某个外部噪声。

6.3.1 随机梯度下降

假设存在某种方式能够计算真实梯度的无偏估计 $\boldsymbol{g}_t$，即

\[\mathbb{E}\left[\boldsymbol{g}_t\right]=\left.\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\right|_{\boldsymbol{\theta}_t} \tag{6.42}\]

然后，便可以使用梯度下降的方法对参数进行更新：

\[\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t-\eta_t \boldsymbol{g}_t \tag{6.43}\]

其中 $\eta_t$ 表示 学习率（learning rate）或 步长（step size）。这被称为 随机梯度下降（stochastic gradient descent, SGD）。

6.3.1.1 如何选择步长

在使用随机梯度下降（SGD）时，需要谨慎地选择学习率以确保优化过程可以收敛。除了选择某个恒定的学习率，可以采用学习率调整策略（learning rate schedule），即根据时间适时调整步长。理论上，SGD收敛的一个充分条件是学习率满足Robbins-Monro条件：

\[\eta_t \rightarrow 0, \frac{\sum_{t=1}^{\infty} \eta_t^2}{\sum_{t=1}^{\infty} \eta_t} \rightarrow 0 \tag{6.44}\]

常用的学习率调整策略包括：

• 分段常数

\[\eta_t=\eta_i, t_i \leq t \leq t_{i+1} \tag{6.45}\]

• 指数衰减

\[\eta_t=\eta_0 e^{-\lambda t} \tag{6.46}\]

• 多项式衰减

\[\eta_t=\eta_0(\beta t+1)^{-\alpha} \tag{6.47}\]

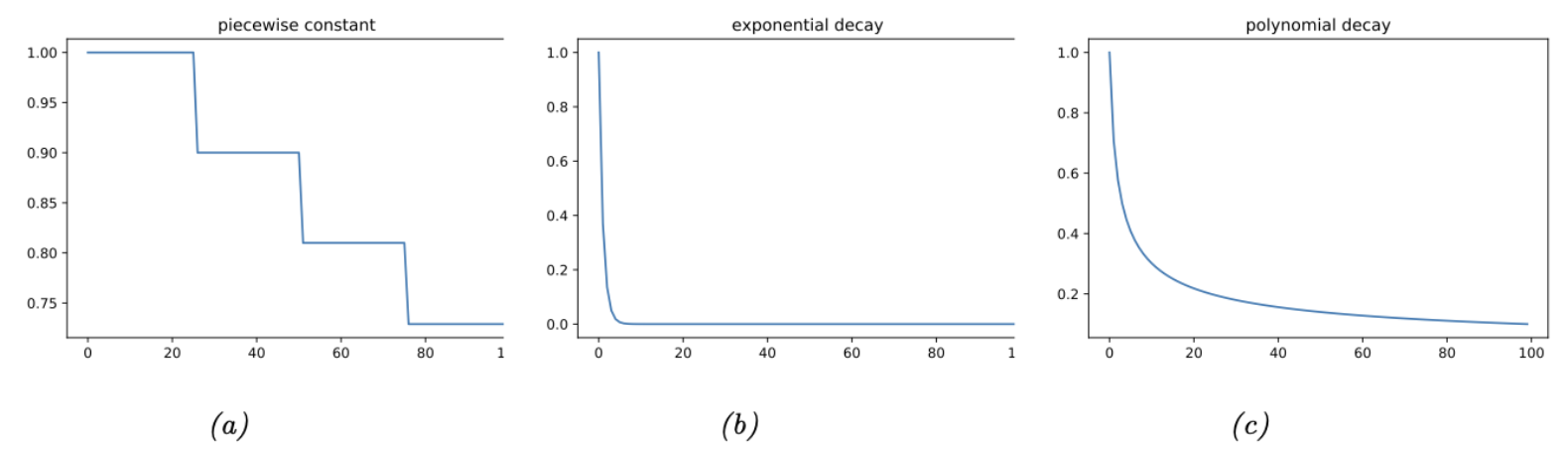
在分段常数策略中，$t_i$ 表示一组时间节点，在这些时间节点上学习率被调整为指定值。例如，令 $\eta_i=\eta_0 \gamma^i$，即每经过一个时间节点，初始学习率就会衰减一个因子 $\gamma$，图6.2a展示了 $\eta_0=1$ 和 $\gamma=0.9$ 时的情况，这被称为步长衰减（step decay）。有时，时间节点是通过估计训练集或验证集损失何时趋于平稳来自适应计算的，这被称为平台期降低（reduce-on-plateau）。对于指数衰减，如图6.2b所示，该策略的下降速度通常太快。如图6.2c所示，一种常见的选择是多项式衰减，图中的 $\alpha=0.5$， $\beta=1$，这也就是平方根策略（square-root schedule），即 $\eta_t=\eta_0 \frac{1}{\sqrt{t+1}}$。更多细节，请参考[Mur22, 第8.4.3节]。

6.3.1.2 减少梯度估计的方差

SGD的收敛可能较慢，因为它依赖于对梯度的随机估计。这种随机性会导致梯度估计的方差过大。为加速收敛，需要减少方差。相关的方法请参考[Mur22, 第8.4.5节]。

6.3.1.3 预条件 SGD

在许多情况下，梯度的幅值大小在不同维度上可能存在显著差异，这对应于损失函数曲面在某些方向上陡峭，而在其他方向上平缓，类似于山谷的地形。此时，通过使用条件矩阵 $\boldsymbol{C}_t$对梯度向量进行缩放，可以加速收敛过程，具体形式如下：

\[\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t-\eta_t \mathbf{C}_t \boldsymbol{g}_t \tag{6.48}\]

这被称为 预条件 SGD（preconditioned SGD）。更多细节参考 [Mur22, Sec 8.4.6]。

6.3.2 SGD用于有限和（finite-sum）目标的优化

在最简单的情况下，式（6.41）中的分布 $q_\boldsymbol{\theta}(\boldsymbol{z})$ 与优化的参数 $\boldsymbol{\theta}$ 本身无关。此时，可以将梯度计算移至期望算子内部，然后通过对 $\boldsymbol{z}$ 进行蒙特卡罗采样实现梯度的计算：

\[\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})=\nabla_{\boldsymbol{\theta}} \mathbb{E}_{q(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})]=\mathbb{E}_{q(\boldsymbol{z})}\left[\nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\right] \approx \frac{1}{S} \sum_{s=1}^S \nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}\left(\boldsymbol{\theta}, \boldsymbol{z}_s\right) \tag{6.49}\]

例如，在经验风险最小化（Empirical Risk Minimization, ERM）问题中，目标函数定义为：

\[\mathcal{L}(\boldsymbol{\theta})=\frac{1}{N} \sum_{n=1}^N \tilde{\mathcal{L}}\left(\boldsymbol{\theta}, \boldsymbol{z}_n\right)=\frac{1}{N} \sum_{n=1}^N \ell\left(\boldsymbol{y}_n, f\left(\boldsymbol{x}_n ; \boldsymbol{\theta}\right)\right) \tag{6.50}\]

其中 \(\boldsymbol{z}_n=(\boldsymbol{x}_n, \boldsymbol{y}_n)\) 表示第 $n$ 个含标签数据， $f$ 表示预测函数。式（6.50）被称为 有限和目标（finite sum objective），形式上可以写成关于经验分布 \(p_{\mathcal{D}}(\boldsymbol{x}, \boldsymbol{y})\) 的损失期望：

\[\mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})] \tag{6.51}\]

因为期望所基于的分布只与数据有关，而与待优化的模型参数无关，所以我们可以使用一个 minibatch $B=|\mathcal{B}|$ 的数据近似梯度：

\[\boldsymbol{g}_t=\nabla \mathcal{L}\left(\boldsymbol{\theta}_t\right)=\frac{1}{B} \sum_{n \in \mathcal{B}} \nabla \ell\left(\boldsymbol{y}_n, f\left(\boldsymbol{x}_n ; \boldsymbol{\theta}\right)\right) \tag{6.52}\]

当数据集规模庞大时，这种方法比 full batch 要快得多，因为它不需要在更新模型之前计算所有 $N$ 个样本的损失[BB08; BB11]。

6.3.3 SGD 用于优化分布的参数

现在假设随机性与优化的参数有关。比方说，在强化学习中，$\boldsymbol{z}$ 可能是一个随机policy $q_\boldsymbol{\theta}$ 输出的 action（见35.3.2节），或者在随机变分推断中， $\boldsymbol{z}$ 可能是一个采样自推理网络 $q_\boldsymbol{\theta}$ 的隐变量（见10.2节）。在这种情况下，梯度为

\[\begin{align} \nabla_\boldsymbol{\theta} \mathbb{E}_{q_\boldsymbol{\theta}(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})] & =\nabla_\boldsymbol{\theta} \int \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) q_\boldsymbol{\theta}(\boldsymbol{z}) d \boldsymbol{z}=\int \nabla_\boldsymbol{\theta} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) q_\boldsymbol{\theta}(\boldsymbol{z}) d \boldsymbol{z} \tag{6.53}\\ & =\int\left[\nabla_\boldsymbol{\theta} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\right] q_\boldsymbol{\theta}(\boldsymbol{z}) d \boldsymbol{z}+\int \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\left[\nabla_\boldsymbol{\theta} q_\boldsymbol{\theta}(\boldsymbol{z})\right] d \boldsymbol{z} \tag{6.54} \end{align}\]

在（6.53）中，我们假设可以交换积分和微分的顺序（参考[Moh+20]）。在（6.54）中，我们使用了导数的乘积法则。

（6.54）中的第一项可以使用蒙特卡洛采样近似：

\[\int\left[\nabla_\theta \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\right] q_\theta(\boldsymbol{z}) d \boldsymbol{z} \approx \frac{1}{S} \sum_{s=1}^S \nabla_\theta \tilde{\mathcal{L}}\left(\boldsymbol{\theta}, \boldsymbol{z}_s\right) \tag{6.55}\]

其中 \(\boldsymbol{z}_s \sim q_{\boldsymbol{\theta}}\)。 需要注意的是，如果 $\tilde{\mathcal{L}}()$ 与 \(\boldsymbol{\theta}\) 无关，则无需考虑该项。

现在考虑第二项，求解关于分布本身的梯度：

\[I \triangleq \int \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\left[\nabla_\boldsymbol{\theta} q_\boldsymbol{\theta}(\boldsymbol{z})\right] d \boldsymbol{z} \tag{6.56}\]

我们无法再使用常规的蒙特卡罗采样进行估计。然而，存在多种近似方案（详见[Moh+20]的全面综述）。我们将在6.3.4节和6.3.5节简要介绍两种常用的方法。

6.3.4 Score 函数估计（REINFORCE）

近似（6.56）的最简单方法是使用 log derivative trick，即等式：

\[\nabla_\boldsymbol{\theta} q_\boldsymbol{\theta}(\boldsymbol{z})=q_\boldsymbol{\theta}(\boldsymbol{z}) \nabla_\boldsymbol{\theta} \log q_\boldsymbol{\theta}(\boldsymbol{z}) \tag{6.57}\]

此时，式（6.56）可以重写成：

\[I=\int \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\left[q_\boldsymbol{\theta}(\boldsymbol{z}) \nabla_{\boldsymbol{\theta}} \log q_\boldsymbol{\theta}(\boldsymbol{z})\right] d \boldsymbol{z}=\mathbb{E}_{q_\boldsymbol{\theta}(\boldsymbol{z})}\left[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) \nabla_{\boldsymbol{\theta}} \log q_\boldsymbol{\theta}(\boldsymbol{z})\right] \tag{6.58}\]

上式被称为评分函数估计器（score function estimator，SFE）[Fu15]。（”评分函数”这一术语表示对数概率分布的梯度，详见第3.3.4.1节解释。）该估计器也被称为似然比梯度估计器（likelihood ratio gradient estimator），或强化梯度估计器（REINFORCE estimator，后一命名的缘由将在第35.3.2节阐明）。此时便可以通过蒙特卡洛方法进行近似：

\[I \approx \frac{1}{S} \sum_{s=1}^S \tilde{\mathcal{L}}\left(\boldsymbol{\theta}, \boldsymbol{z}_s\right) \nabla_{\boldsymbol{\theta}} \log q_{\boldsymbol{\theta}}\left(\boldsymbol{z}_s\right) \tag{6.59}\]

其中 \(\boldsymbol{z}_s \sim q_{\boldsymbol{\theta}}\)。 在式（6.59）中，仅要求采样分布是可微的，而目标函数 \(\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})\) 本身无需可微。这使得该方法能够适用于黑盒随机优化问题，例如变分优化（variational optimization）（补充材料的第6.4.3节）、黑盒变分推断（black-box variational inference）（第10.2.3节）、强化学习（第35.3.2节）等场景。

6.3.4.1 控制变量

score 函数估计的结果可能存在较大方差。缓解的方式是使用 控制变量（control variates），即使用下式替代 $\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})$

\[\hat{\tilde{L}}(\boldsymbol{\theta}, \boldsymbol{z})=\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})-c(b(\boldsymbol{\theta}, \boldsymbol{z})-\mathbb{E}[b(\boldsymbol{\theta}, \boldsymbol{z})]) \tag{6.60}\]

其中 $b(\boldsymbol{\theta}, \boldsymbol{z})$ 被称为与 $\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})$ 相关的 baseline function，$c\gt0$ 为系数。考虑到 $\mathbb{E}[\hat{\tilde{\mathcal{L}}}(\boldsymbol{\theta}, \boldsymbol{z})]=\mathbb{E}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})]$，我们可以使用 $\hat{\tilde{\mathcal{L}}}$ 计算关于 $\tilde{\mathcal{L}}$ 梯度的无偏估计。使用前者的优势是新的估计方差更小，参考 11.6.3 节。

6.3.4.2 Rao-Blackwellization

假设 $q_\boldsymbol{\theta}(\boldsymbol{z})$ 是一个离散分布。此时，目标函数变为：$\mathcal{L}(\boldsymbol{\theta})=\sum_\boldsymbol{z} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) q_\boldsymbol{\theta}(\boldsymbol{z})$。我们可以直接计算梯度：$\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})=\sum_{\boldsymbol{z}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) \nabla_\theta q_\theta(\boldsymbol{z})$。当然，如果 $\boldsymbol{z}$ 的取值空间规模呈指数级增长（例如，字符串空间上进行优化），这个表达式将难以计算。解决的方法是，假设取值空间可以被拆分成两个部分：发生概率高但规模小的样本集合 $S_1$，发生概率低但规模大的样本集合 $S_2$。对于前者，可以枚举 $S_1$中的值，而对于后者，可以使用评分函数估计器（score function estimator）：

\[\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})=\sum_{\boldsymbol{z} \in S_1} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) \nabla_{\boldsymbol{\theta}} q_{\boldsymbol{\theta}}(\boldsymbol{z})+\mathbb{E}_{q_{\boldsymbol{\theta}}\left(\boldsymbol{z} \mid \boldsymbol{z} \in S_2\right)}\left[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) \nabla_{\boldsymbol{\theta}} \log q_{\boldsymbol{\theta}}(\boldsymbol{z})\right] \tag{6.61}\]

为计算第二个期望项，我们可以对从 $q_\boldsymbol{\theta}(\boldsymbol{z})$ 中得到的样本使用拒绝采样（rejection sampling）。 该方法属于一种Rao-Blackwell化形式（如[Liu+19b]所示），与标准评分函数估计器（SFE）相比能降低方差（关于Rao-Blackwell化的详细说明参见第11.6.2节）。

6.3.5 重参数化trick

即使使用控制变量（control variate），评分函数估计器（SFE）的方差可能依然较大。本节介绍一种方差更小的估计器，该估计器需要目标函数 $\tilde{L}(\boldsymbol{\theta}, \boldsymbol{z})$ 对 $\boldsymbol{z}$ 同样可微。与此同时，随机变量 $\boldsymbol{z}$ 可以通过以下方式采样获得：先通过与 $\boldsymbol{\theta}$ 无关的噪声分布 $q_0$ 得到随机噪声 $\boldsymbol{\epsilon}$，再通过确定性可微函数 $\boldsymbol{z} = g(\boldsymbol{\theta}, \boldsymbol{\epsilon})$ 得到 $\boldsymbol{z}$ 。例如，为了得到样本 $\boldsymbol{z} \sim \mathcal{N}(\mu, \sigma^2)$，我们可以先采样 $\boldsymbol{\epsilon} \sim \mathcal{N}(0, 1)$，然后计算

\[\boldsymbol{z}=g(\boldsymbol{\theta}, \boldsymbol{\epsilon})=\mu+\sigma \boldsymbol{\epsilon} \tag{6.62}\]

其中 $\boldsymbol{\theta}=(\mu, \sigma)$。这允许我们重写随机目标函数：

\[\mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{q_\boldsymbol{\theta}(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})]=\mathbb{E}_{q_0(\boldsymbol{\epsilon})}[\tilde{\mathcal{L}}(\boldsymbol{\theta}, g(\boldsymbol{\theta}, \boldsymbol{\epsilon}))] \tag{6.63}\]

考虑到 $q_0(\boldsymbol{\epsilon})$ 与 $\boldsymbol{\theta}$ 无关，我们可以将梯度算子移到期望内部，并通过蒙特卡洛方法近似：

\[\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{q_0(\boldsymbol{\epsilon})}\left[\nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, g(\boldsymbol{\theta}, \boldsymbol{\epsilon}))\right] \approx \frac{1}{S} \sum_{s=1}^S \nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}\left(\boldsymbol{\theta}, g\left(\boldsymbol{\theta}, \boldsymbol{\epsilon}_s\right)\right) \tag{6.64}\]

其中 $\boldsymbol{\epsilon}_s \sim q_0$。这种方法被称为重参数化梯度（reparameterization gradient）或路径导数（pathwise derivative）[Gla03; Fu15; KW14; RMW14a; TLG14; JO18; FMM18]，在变分推断（第10.2.1节）中被广泛使用。关于此类方法的综述，可参阅[Moh+20]。

值得注意的是，TensorFlow Probability库（同时提供JAX接口）支持重参数化分布。因此，可以如??6.1所示直接编写代码。

6.3.5.1 案例

为了进一步解释重参数化技巧，举个简单例子，假设损失函数 $\tilde{\mathcal{L}}(z) = z^2 - 3z$， 其期望值 $\mathcal{L}(\boldsymbol{\theta}) = \mathbb{E}_{\mathcal{N}(z|\mu,v)}[\tilde{\mathcal{L}}(z)]$， 其中参数 $\boldsymbol{\theta} = (\mu, v)$ 且 $v = \sigma^2$。 假设我们需要计算

\[\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})=\left[\frac{\partial}{\partial \mu} \mathbb{E}[\tilde{\mathcal{L}}(z)], \frac{\partial}{\partial v} \mathbb{E}[\tilde{\mathcal{L}}(z)]\right] \tag{6.65}\]

由于高斯分布是可重参数化的，我们可以先采样 $z \sim \mathcal{N}(z|\mu, v)$， 然后使用自动微分计算每个梯度项，最后再求期望。

不过对于高斯分布这一特殊情况，也可以直接计算梯度向量。具体而言，根据第6.4.5.1节介绍Bonnet定理：

\[\frac{\partial}{\partial \mu} \mathbb{E}[\tilde{\mathcal{L}}(z)]=\mathbb{E}\left[\frac{\partial}{\partial z} \tilde{\mathcal{L}}(z)\right] \tag{6.66}\]

类似地， Price 定理表明

\[\frac{\partial}{\partial v} \mathbb{E}[\tilde{\mathcal{L}}(z)]=0.5 \mathbb{E}\left[\frac{\partial^2}{\partial z^2} \tilde{\mathcal{L}}(z)\right] \tag{6.67}\]

在 gradient_expected_value_gaussian.ipynb 中，我们通过实验验证了这两种方法在数值上是等价的，这与理论预测完全一致。

6.3.5.2 全方差

要计算式(6.64)中期望项内的梯度，我们需要使用全导数，因为函数 $\tilde{\mathcal{L}}$ 同时与 $\boldsymbol{\theta}$ 和 $\boldsymbol{z}$ 有关。回顾一下，对于形如 $\tilde{\mathcal{L}}(\theta_1,…,\theta_{d_\psi},z_1(\boldsymbol{\theta}),…,z_{d_z}(\boldsymbol{\theta}))$ 的函数，关于 $\theta_i$ 的全导数由链式法则给出：

\[{\frac{\partial \tilde{\mathcal{L}}^{\mathrm{TD}}}{\partial \theta_i}}=\frac{\partial \tilde{\mathcal{L}}}{\partial \theta_i}+\sum_j \frac{\partial \tilde{\mathcal{L}}}{\partial z_j} \frac{\partial z_j}{\partial \theta_i} \tag{6.68}\]

所以

\[\nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})^{\mathrm{TD}}=\nabla_{\boldsymbol{z}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) \mathbf{J}+\nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) \tag{6.69}\]

其中 $\mathbf{J}=\frac{\partial \boldsymbol{z}^{\top}}{\partial \boldsymbol{\theta}}$ 是一个 $d_z \times d_\psi$ 大小的雅各比矩阵：

\[\mathbf{J}=\left(\begin{array}{ccc} \frac{\partial \boldsymbol{z}_1}{\partial \boldsymbol{\theta}_1} & \cdots & \frac{\partial \boldsymbol{z}_1}{\partial \boldsymbol{\theta}_{d_\psi}} \\ \vdots & \ddots & \vdots \\ \frac{\partial \boldsymbol{z}_{d_z}}{\partial \boldsymbol{\theta}_{d_\psi}} & \cdots & \frac{\partial \boldsymbol{z}_{d_z}}{\partial \boldsymbol{\theta}_{d_\psi}} \end{array}\right) \tag{6.70}\]

我们将在第6.3.5.3节中利用这一分解方法，针对变分推断这一特殊情况推导出方差更小的梯度估计器。

6.3.5.3 “Sticking the landing” 估计器

本节我们将探讨变分推断（参见第10.2节）中的特殊情况。对于单个隐变量样本 $\boldsymbol{z}$ ，其证据下确界（ELBO）的形式为：

\[\tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z})=\log p(\boldsymbol{z}, \boldsymbol{x})-\log q(\boldsymbol{z} \mid \boldsymbol{\theta}) \tag{6.71}\]

其中，$\boldsymbol{\theta}$ 表示变分后验分布的参数。其梯度表达式为：

\[\begin{align} \nabla_{\boldsymbol{\theta}} \tilde{\mathcal{L}}(\boldsymbol{\theta}, \boldsymbol{z}) & =\nabla_{\boldsymbol{\theta}}[\log p(\boldsymbol{z}, \boldsymbol{x})-\log q(\boldsymbol{z} \mid \boldsymbol{\theta})] \tag{6.72}\\ & =\underbrace{\nabla_{\boldsymbol{z}}[\log p(\boldsymbol{z}, \boldsymbol{x})-\log q(\boldsymbol{z} \mid \boldsymbol{\theta})] \mathbf{J}}_{\text {path derivative }}-\underbrace{\nabla_{\boldsymbol{\theta}} \log q(\boldsymbol{z} \mid \boldsymbol{\theta})}_{\text {score function }} \tag{6.73} \end{align}\]

式（6.73）的第一项表示 \(\boldsymbol{\theta}\) 通过生成样本 $\boldsymbol{z}$ 对目标函数产生的间接影响。第二项是 $\boldsymbol{\theta}$ 对目标函数产生的直接影响。第二项的期望值等于零（因为它是评分函数，参考式(3.44)），但对于有限样本量可能并不等于零，即使当 \(q(\boldsymbol{z}|\boldsymbol{\theta})=p(\boldsymbol{z}|\boldsymbol{x})\) 是真实后验时也是如此。在[RWD17]中，作者提出通过舍弃第二项来构建一个更低方差的估计器。这可以通过使用 \(\log q(\boldsymbol{z}|\boldsymbol{\theta}^\prime)\) 来实现，其中 $\boldsymbol{\theta}^\prime$ 是与梯度计算”断开连接”的关于 $\boldsymbol{\theta}$ 副本。伪代码为：

\[\begin{align} \boldsymbol{\epsilon} & \sim q_0(\boldsymbol{\epsilon}) \tag{6.74}\\ \boldsymbol{z} & =g(\boldsymbol{\epsilon}, \boldsymbol{\theta}) \tag{6.75}\\ \boldsymbol{\theta}^{\prime} & =\text { stop-gradient }(\boldsymbol{\theta}) \tag{6.76}\\ \boldsymbol{g} & =\nabla_{\boldsymbol{\theta}}\left[\log p(\boldsymbol{z}, \boldsymbol{x})-\log q\left(\boldsymbol{z} \mid \boldsymbol{\theta}^{\prime}\right)\right] \tag{6.77} \end{align}\]

这种方法被称为”着陆固定”（Sticking the Landing，STL）估计器。需要注意的是，STL估计器并非总是优于不含梯度截断项的”标准”估计器。在[GD20]中，研究者提出使用加权组合的估计器，其权重经过优化，可在固定计算量下实现方差最小化。

6.3.6 Gumbel softmax trick

当处理离散变量时，我们无法直接使用重参数化技巧（reparameterization trick），因为重参数化技巧需要保证分布关于 $\boldsymbol{z}$ 是可微的。不过，通过将离散变量适当松弛（relax）为连续变量，我们通常仍能应用该技巧，具体方法如下所述：

考虑一个$K$维的one-hot向量 $\boldsymbol{d}$， 其中每个元素 $d_k \in {0,1}$ 且满足 $\sum_{k=1}^K d_k = 1$。 这种表示法可用于描述一个$K$元变量 $d$。假设其概率分布为 $P(d) = \text{Cat}(d|\pi)$， 其中 $\pi_k = P(d_k=1)$， 同时满足 $0 \leq \pi_k \leq 1$。 或者，我们也可以用 $(\alpha_1,…,\alpha_K)$ 来参数化这个分布，其中 $\pi_k = \alpha_k/(\sum_{k’=1}^K \alpha_{k’})$。 这种参数化形式记作 $d \sim \text{Cat}(d|\boldsymbol{\alpha})$。

我们可以通过以下方式从该分布中采样一个one-hot向量 $\boldsymbol{d}$：

\[\boldsymbol{d}=\operatorname{onehot}\left(\underset{k}{\operatorname{argmax}}\left[\epsilon_k+\log \alpha_k\right]\right) \tag{6.78}\]

其中 $\epsilon_k \sim \text{Gumbel}(0,1)$ 是从Gumbel分布[Gum54]中采样得到的随机变量。我们可以通过以下步骤生成这样的样本：先采样$u_k \sim \text{Unif}(0,1)$，然后计算$\epsilon_k = -\log(-\log(u_k))$，这种方法被称为Gumbel-max技巧[MTM14]，它为类别分布提供了一种可重参数化的表示方法。

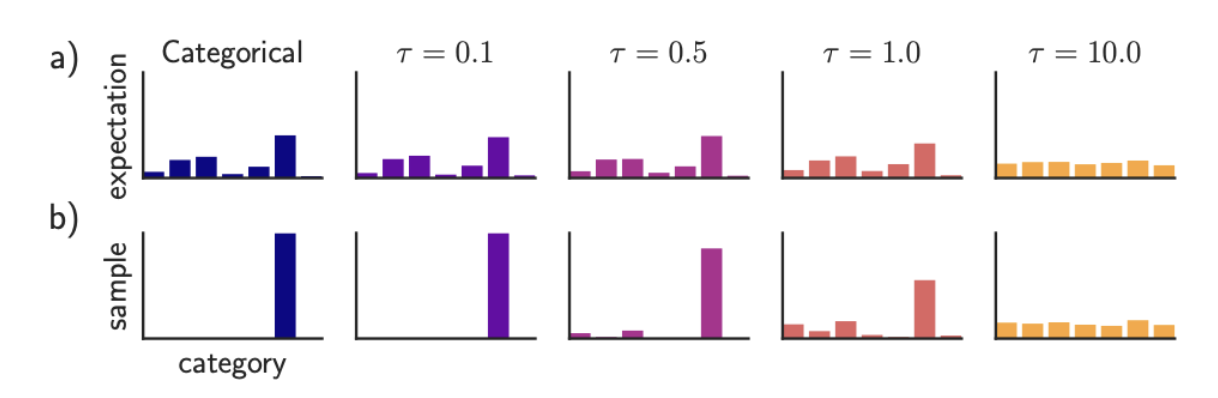
遗憾的是，$\text{argmax}$ 函数的导数在除边界外的所有位置均为零，而在边界处导数无定义。不过，若我们用 $\text{softmax}$ 替代 $\text{argmax}$，并将离散的one-hot向量 $\boldsymbol{d}$ 松弛为连续变量$\boldsymbol{x} \in \Delta^{K-1}$（其中 $\Delta^{K-1} = {\boldsymbol{x} \in \mathbb{R}^K: x_k \in [0,1], \sum_{k=1}^K x_k = 1}$表示$K$维概率单纯形），则可表示为：

\[x_k=\frac{\exp \left(\left(\log \alpha_k+\epsilon_k\right) / \tau\right)}{\sum_{k^{\prime}=1}^K \exp \left(\left(\log \alpha_{k^{\prime}}+\epsilon_{k^{\prime}}\right) / \tau\right)} \tag{6.79}\]

其中$\tau > 0$表示温度参数。这种分布被称为 Gumbel-softmax分布[JGP17] 或 concrete分布[MMT17]。如图6.3所示，当$\tau \to 0$时，该分布会平滑地逼近离散分布。

现在我们可以用 $f(\boldsymbol{x})$ 替代 $f(\boldsymbol{d})$，并且能够计算关于 $\boldsymbol{x}$ 的重参数化梯度。

6.3.7 Stochastic computation graphs

我们可以将包含确定性和随机性组件的任意函数表示为随机计算图（stochastic computation graph）。通过扩展自动微分算法（第6.2节），结合评分函数估计（第6.3.4节）和重参数化技巧（第6.3.5节），即可为复杂的嵌套函数计算蒙特卡洛梯度。具体实现细节可参考[Sch+15a; Gaj+19]。

6.3.8 Straight-through estimator

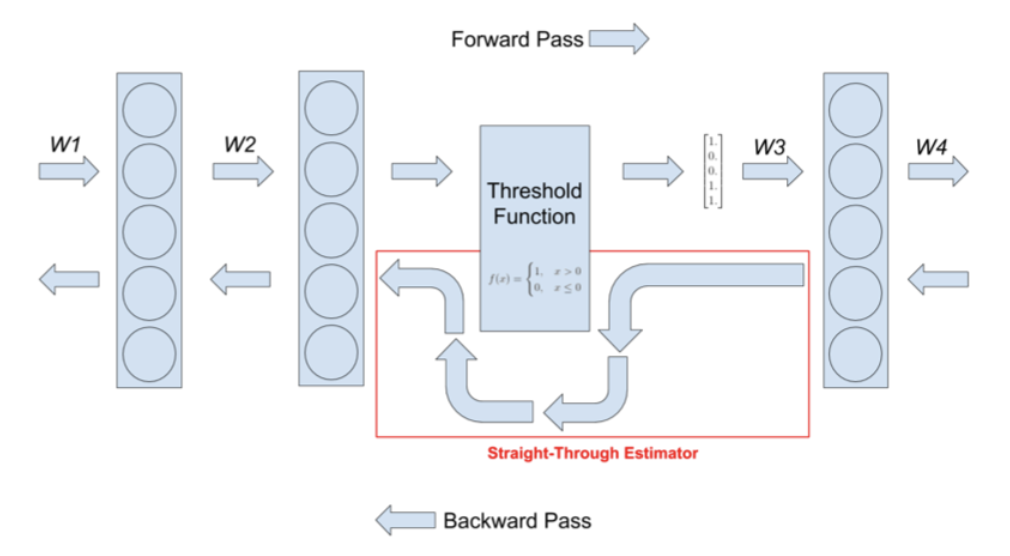
本节将探讨如何近似关于量化版本的信号的梯度。例如，考虑以下阈值函数（该函数将输出二值化）：

\[f(x)= \begin{cases}1 & \text { if } x>0 \\ 0 & \text { if } x \leq 0\end{cases} \tag{6.80}\]

该函数没有明确定义的梯度。不过，我们可以使用[Ben13]提出的直通估计器（straight-through estimator）进行近似。其核心思想是：在反向传播计算中，将 $g(x) = f’(x)$（其中$f’(x)$ 表示 $f$ 对输入的导数）替换为 $g(x) = x$。可视化结果见图6.4，关于该近似有效性的分析可参考[Yin+19b]。

实际应用中，我们有时会用硬双曲正切函数（hard tanh）替代$g(x) = x$，其定义为：

\[\operatorname{HardTanh}(x)= \begin{cases}x & \text { if }-1 \leq x \leq 1 \\ 1 & \text { if } x>1 \\ -1 & \text { if } x<-1\end{cases} \tag{6.81}\]

这样可以确保反向传播的梯度不会过大。该方法在离散自编码器中的应用详见第21.6节。

6.4 自然梯度下降

本节将讨论自然梯度下降法（Natural Gradient Descent, NGD）[Ama98]，这是一种用于优化（条件）概率分布 $p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x})$ 参数的二阶方法。其核心思想是：通过度量分布之间的差异（而非直接比较参数值）来计算参数的优化方向。

以两个高斯分布 $p_{\boldsymbol{\theta}}=p(y \mid \mu, \sigma)$ 和 $p_{\boldsymbol{\theta}^{\prime}}=p\left(y \mid \mu^{\prime}, \sigma^{\prime}\right)$ 为例，参数向量的（平方）欧氏距离可分解成两个部分—— $\left|\boldsymbol{\theta}-\boldsymbol{\theta}^{\prime}\right|^2=\left(\mu-\mu^{\prime}\right)^2+\left(\sigma-\sigma^{\prime}\right)^2$。然而，高斯分布的定义形式为 $\exp(-\frac{1}{2\sigma^2}(y-\mu)^2)$，因此期望 $\mu$ 的变化需要相对于标准差 $\sigma$ 来衡量。图6.5(a-b)直观展示了这种情况：两组高斯分布（虚线与实线）的期望都相差 $\delta$，其中图6.5(a)的方差 $\sigma^2$ 较图6.5(b)小。显然，当方差较小时，$\delta$ 的取值（对分布形态的）影响更为显著。由此可见，这两个参数存在相互影响，而欧氏距离无法捕捉这种关系。对于深度学习等复杂模型，这个问题会更加突出。通过建模参数之间相关性，自然梯度下降法（NGD）的收敛速度远超其他梯度下降的优化方法。

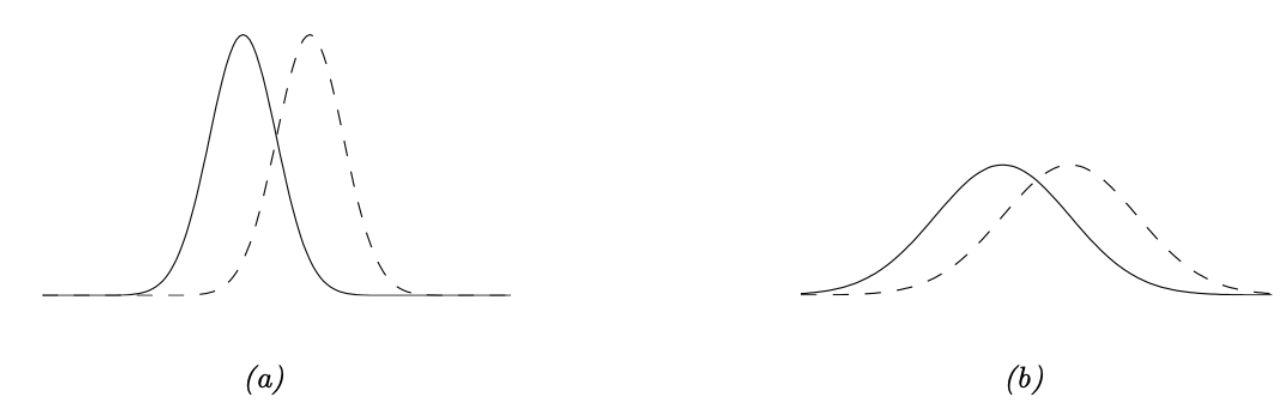
6.4.1 自然梯度的定义

自然梯度下降（NGD）的核心在于使用KL散度（Kullback-Leibler divergence）来衡量两个概率分布之间的距离。如第5.1.9节所示，KL散度可以通过Fisher信息矩阵（FIM）实现近似。具体而言，对于任意给定输入 $\boldsymbol{x}$，有：

\[D_{\mathbb{KL}}\left(p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x}) \| p_{\boldsymbol{\theta}+\boldsymbol{\delta}}(\boldsymbol{y} \mid \boldsymbol{x})\right) \approx \frac{1}{2} \boldsymbol{\delta}^{\top} \mathbf{F}_{\boldsymbol{x}} \boldsymbol{\delta} \tag{6.82}\]

其中 $\mathbf{F}_x$ 表示 FIM：

\[\mathbf{F}_{\boldsymbol{x}}(\boldsymbol{\theta})=-\mathbb{E}_{p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x})}\left[\nabla^2 \log p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x})\right]=\mathbb{E}_{p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x})}\left[\left(\nabla \log p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x})\right)\left(\nabla \log p_{\boldsymbol{\theta}}(\boldsymbol{y} \mid \boldsymbol{x})\right)^{\top}\right] \tag{6.83}\]

我们可以通过 $\frac{1}{2} \boldsymbol{\delta}^{\top} \mathbf{F} \boldsymbol{\delta}$ 计算参考分布与更新分布之间的平均KL散度，其中 $\mathbf{F}$ 表示平均Fisher信息矩阵：

\[\mathbf{F}(\boldsymbol{\theta})=\mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{x})}\left[\mathbf{F}_{\boldsymbol{x}}(\boldsymbol{\theta})\right] \tag{6.84}\]

自然梯度下降（NGD）采用Fisher信息矩阵（FIM）的逆矩阵作为预条件矩阵，其参数更新形式如下：

\[\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t-\eta_t \mathbf{F}\left(\boldsymbol{\theta}_t\right)^{-1} \boldsymbol{g}_t \tag{6.85}\]

其中

\[\mathbf{F}^{-1} \boldsymbol{g}_t=\mathbf{F}^{-1} \nabla \mathcal{L}\left(\boldsymbol{\theta}_t\right) \triangleq \tilde{\nabla} \mathcal{L}\left(\boldsymbol{\theta}_t\right) \tag{6.86}\]

被称为自然梯度（natural gradient）。

费舍尔信息矩阵（Fisher Information Matrix, FIM）是统计学和信息几何中的一个核心概念，用于量化概率分布模型中观测数据所携带的关于参数的信息量。

6.4.2 关于NGD的解释

6.4.2.1 NGD 是一种信赖域优化方法

补充材料的第6.1.3.1节证明标准梯度下降可解释为：在参数变化的 $l_2$ 范数约束下，对目标函数进行线性近似优化。具体而言，若设 $\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t+\boldsymbol{\delta}$，则优化问题可定义为：

\[M_t(\boldsymbol{\delta})=\mathcal{L}\left(\boldsymbol{\theta}_t\right)+\boldsymbol{g}_t^{\top} \boldsymbol{\delta}+\eta\|\boldsymbol{\delta}\|_2^2 \tag{6.87}\]

现在，将平方距离替换为基于FIM的平方距离 $|\boldsymbol{\delta}|_F^2=\boldsymbol{\delta}^{\top} \mathbf{F} \boldsymbol{\delta}$。这等价于在白化坐标系（whitened coordinate system*） $\phi=\mathbf{F}^{\frac{1}{2}} \boldsymbol{\theta}$ 中的平方欧式距离，因为：

\[\left\|\boldsymbol{\phi}_{t+1}-\boldsymbol{\phi}_t\right\|_2^2=\left\|\mathbf{F}^{\frac{1}{2}}\left(\boldsymbol{\theta}_t+\boldsymbol{\delta}\right)-\mathbf{F}^{\frac{1}{2}} \boldsymbol{\theta}_t\right\|_2^2=\left\|\mathbf{F}^{\frac{1}{2}} \boldsymbol{\delta}\right\|_2^2=\|\boldsymbol{\delta}\|_F^2 \tag{6.88}\]

新的优化目标定义为

\[M_t(\boldsymbol{\delta})=\mathcal{L}\left(\boldsymbol{\theta}_t\right)+\boldsymbol{g}_t^{\top} \boldsymbol{\delta}+\eta \boldsymbol{\delta}^{\top} \mathbf{F} \boldsymbol{\delta} \tag{6.89}\]

求解 $\nabla_\boldsymbol{\delta} M_t(\boldsymbol{\delta})=\mathbf{0}$ 并得到参数的更新向量

\[\boldsymbol{\delta}_t=-\eta \mathbf{F}^{-1} \boldsymbol{g}_t \tag{6.90}\]

这等同于自然梯度的方向。因此，我们可以将自然梯度下降（NGD）视为一种信赖域方法——其中采用目标函数的一阶近似，并在约束条件中使用基于FIM的距离度量。

在上述推导中，我们假设 $\mathbf{F}$ 是常数矩阵。但在大多数实际问题中，由于我们是在黎曼流形（Riemannian manifold）这一弯曲空间中进行优化，$\mathbf{F}$ 会随空间位置变化而变化。尽管仅使用目标函数的一阶近似，但对于特定模型，我们仍能高效计算FIM，从而捕捉曲率信息。

---

补充阅读

1. 标准梯度下降法的重定义

   在标准梯度下降法中，参数的更新规则定义为：

   \[\theta_{t+1}=\theta_t-\alpha \nabla_\theta \mathcal{L}\left(\theta_t\right) \tag{a}\]

   其中 $\alpha$ 表示学习率，$\nabla_\theta \mathcal{L}\left(\theta_t\right)$ 表示 $\mathcal{L}(\theta)$ 在 $\theta_t$ 的梯度。

   接下来，我们将证明上述更新规则，实际上是某个优化问题的最优解，该优化问题定义为：

   \[\theta_{t+1}=\arg \min _\theta\left[\mathcal{L}\left(\theta_t\right)+\nabla_\theta \mathcal{L}\left(\theta_t\right)^T\left(\theta-\theta_t\right)+\frac{1}{2 \alpha}\left\|\theta-\theta_t\right\|_2^2\right] \tag{b}\]

​ 上式第一项是常数，第二项是目标函数在当前点的一阶泰勒展开，第三项是对参数变化量的L2范数惩罚。对上述优化目标求导并令导数为0，：

\[\nabla_\theta\left[\nabla_\theta \mathcal{L}\left(\theta_t\right)^T\left(\theta-\theta_t\right)+\frac{1}{2 \alpha}\left\|\theta-\theta_t\right\|_2^2\right]=0 \tag{c}\]

​ 得到：

\[\nabla_\theta \mathcal{L}\left(\theta_t\right)+\frac{1}{\alpha}\left(\theta-\theta_t\right)=0 \quad \Rightarrow \quad \theta=\theta_t-\alpha \nabla_\theta \mathcal{L}\left(\theta_t\right) \tag{d}\]

1. 标准梯度下降的几何意义

   线性近似：假设目标函数在当前点附近是线性的；

   L2惩罚：限制参数更新的幅度，防止因线性近似不准确导致发散；

   学习率作用：$\alpha$ 越小，L2惩罚越大，参数更新幅度越小，优化过程越保守。

2. 自然梯度下降的区别

   自然梯度下降的 L2 惩罚替换为基于Fisher信息矩阵的黎曼度量：$\left|\theta-\theta_t\right|_{G(\theta)}^2=(\theta-\left.\theta_t\right)^T G(\theta)\left(\theta-\theta_t\right)$，它适应参数空间的几何结构。

---

6.4.2.2 NGD 是一种高斯牛顿方法

若 $p(\boldsymbol{y}|\boldsymbol{x},\boldsymbol{\theta})$ 属于指数族分布，且其自然参数 $\boldsymbol{\eta} = f(\boldsymbol{x},\boldsymbol{\theta})$， 则可以证明[Hes00; PB14]：自然梯度下降（NGD）与广义高斯-牛顿法（GGN，第17.3.2节）完全等价。此外，在线学习场景下，如[Oll18]所示，这些方法等价于使用扩展卡尔曼滤波器进行序列贝叶斯推断。

6.4.3 NGD的优势

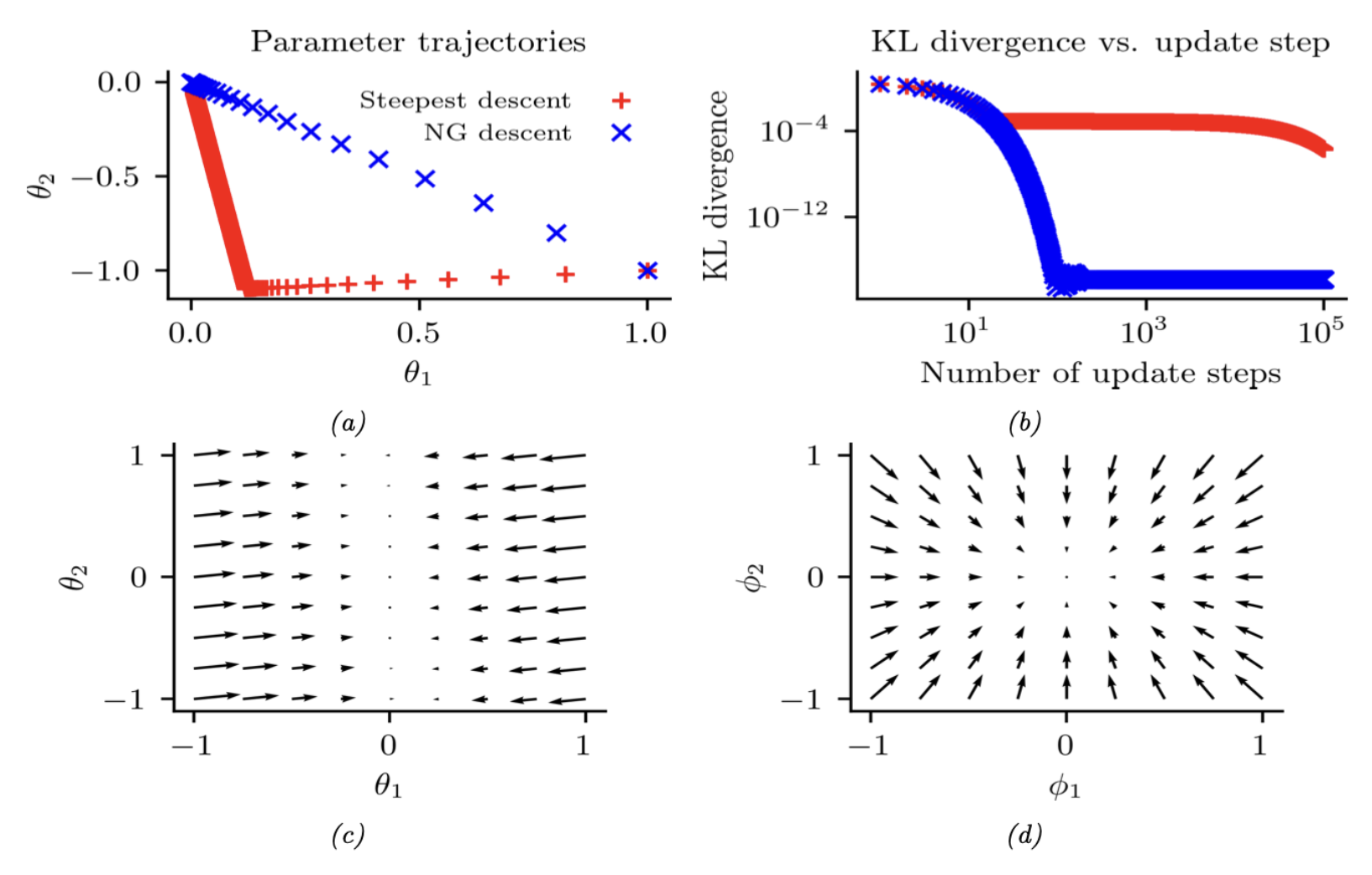
使用Fisher信息矩阵（FIM）而非Hessian矩阵作为预条件矩阵具有两大优势：首先，$\mathbf{F}$ 始终是正定矩阵，而 $\mathbf{H}$ 在鞍点（高维空间中普遍存在）可能出现负特征值；其次，由于 $\mathbf{F}$ 是梯度向量外积的期望（关于经验分布），易于通过小批量数据在线近似。这与基于Hessian的方法[Byr+16; Liu+18a]形成鲜明对比——后者对小批量近似引入的噪声更为敏感。

此外，与信赖域优化的关联表明，自然梯度下降（NGD）以对预测最重要的方式更新参数，这使得该方法能够在参数空间的非信息区域采取更大步长，从而有助于避免陷入平坦区域。这也能缓解参数高度相关性导致的问题。

例如，考虑[SD12]提出的具有高度耦合参数化的二维高斯分布：

\[p(\boldsymbol{x} ; \boldsymbol{\theta})=\frac{1}{2 \pi} \exp \left[-\frac{1}{2}\left(x_1-\left[3 \theta_1+\frac{1}{3} \theta_2\right]\right)^2-\frac{1}{2}\left(x_2-\left[\frac{1}{3} \theta_1\right]\right)^2\right] \tag{6.91}\]

优化目标为交叉熵损失：

\[\mathcal{L}(\boldsymbol{\theta})=-\mathbb{E}_{p^*(\boldsymbol{x})}[\log p(\boldsymbol{x} ; \boldsymbol{\theta})] \tag{6.92}\]

对应的梯度为

\[\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})\binom{=\mathbb{E}_{p^*(\boldsymbol{x})}\left[3\left(x_1-\left[3 \theta_1+\frac{1}{3} \theta_2\right]\right)+\frac{1}{3}\left(x_2-\left[\frac{1}{3} \theta_1\right]\right)\right]}{\mathbb{E}_{p^*(\boldsymbol{x})}\left[\frac{1}{3}\left(x_1-\left[3 \theta_1+\frac{1}{3} \theta_2\right]\right)\right]} \tag{6.93}\]

假设真实分布 $p^*(\boldsymbol{x}) = p(\boldsymbol{x}; [0, 0])$，则Fisher信息矩阵为常数矩阵，其表达式为：

\[\mathbf{F}=\left(\begin{array}{cc} 3^2+\frac{1}{3^2} & 1 \\ 1 & \frac{1}{3^2} \end{array}\right) \tag{6.94}\]

图6.6对比了在$\theta$空间的最速下降法与自然梯度法（等价于$\phi$空间的最速下降）。两种方法均使用 $\theta = (1, -1)$ 初始化，全局最优解$\theta = (0, 0)$。从图中不难发现，自然梯度法（蓝色点）能以更短路径快速收敛至最优解，而传统最速下降法则呈现迂回路线。同时可观察到，白化参数空间中的梯度场更接近”球形”，这使得下降过程更简单高效。

最后要注意的是，由于自然梯度下降（NGD）对概率分布的参数化方式具有不变性，因此即使对高斯分布采用标准参数化，我们仍会得到相同的结果。这一特性在概率模型较为复杂时（例如深度神经网络，参见[SSE18]）尤为有用。

6.4.4 近似自然梯度

自然梯度下降（NGD）的主要缺点在于计算（或求逆）费舍尔信息矩阵（FIM）的成本。为了加速计算，现有方法通常对FIM的结构进行假设，使其能高效求逆。例如：[LeC+98] 在神经网络训练中使用对角近似；[RMB08] 采用低秩加块对角近似；[GS15] 假设梯度的协方差可通过树宽较小的有向高斯图模型建模（即费舍尔矩阵的Cholesky分解是稀疏的）。

[MG15]提出了KFAC方法，其全称为”克罗内克分解近似曲率”（Kronecker factored approximate curvature）。该方法将深度神经网络的费舍尔信息矩阵（FIM）近似为块对角矩阵，其中每个区块是两个小矩阵的克罗内克积。KFAC方法已在神经网络监督学习[GM16; BGM17; Geo+18; Osa+19b]和策略网络强化学习[Wu+17]中展现出良好效果。[AKO18]的均值场分析为KFAC近似提供了理论依据。此外，[ZMG19]证明当过参数化时（即网络具有插值特性），KFAC能收敛到深度神经网络的全局最优解。

一种更简单的方法是用经验分布替代模型分布来近似FIM。具体而言，定义： $p_D(x,y) = \frac{1}{N}\sum_{n=1}^N \delta_{x_n}(x)\delta_{y_n}(y)$，$p_D(x) = \frac{1}{N}\sum_{n=1}^N \delta_{x_n}(x)$，$p_\theta(x,y) = p_D(x)p(y|x,\theta)$。则可按如下方式计算经验Fisher矩阵[Mar16]：

\[\begin{align} \mathbf{F} & =\mathbb{E}_{p_{\boldsymbol{\theta}}(\boldsymbol{x}, \boldsymbol{y})}\left[\nabla \log p(\boldsymbol{y} \mid \boldsymbol{x}, \boldsymbol{\theta}) \nabla \log p(\boldsymbol{y} \mid \boldsymbol{x}, \boldsymbol{\theta})^{\mathrm{\top}}\right] \tag{6.95}\\ & \approx \mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{x}, \boldsymbol{y})}\left[\nabla \log p(\boldsymbol{y} \mid \boldsymbol{x}, \boldsymbol{\theta}) \nabla \log p(\boldsymbol{y} \mid \boldsymbol{x}, \boldsymbol{\theta})^{\mathrm{\top}}\right] \tag{6.96}\\ & =\frac{1}{|\mathcal{D}|} \sum_{(\boldsymbol{x}, \boldsymbol{y}) \in \mathcal{D}} \nabla \log p(\boldsymbol{y} \mid \boldsymbol{x}, \boldsymbol{\theta}) \nabla \log p(\boldsymbol{y} \mid \boldsymbol{x}, \boldsymbol{\theta})^{\top} \tag{6.97} \end{align}\]

这种近似方法被广泛使用，因为其计算简单。具体而言，我们可以利用梯度向量的平方来计算对角近似（类似于AdaGrad，但仅使用当前梯度而非梯度的移动平均；在随机优化中，后者是更好的方法）。

遗憾的是，经验Fisher矩阵的效果不如真实Fisher矩阵[KBH19; Tho+19]。原因在于，当参数空间进入梯度为零的平坦区域时，经验Fisher矩阵会变得奇异（不可逆），导致优化算法陷入停滞。而真实Fisher矩阵通过对输出（$\boldsymbol{y}$）求期望来边缘化 $\boldsymbol{y}$ 的影响，因此即便参数微小变化导致输出分布改变，它仍能捕捉到这种变化。这正是自然梯度法（natural gradient）比普通梯度法更能逃离“平坦区域”的原因。

另一种策略是精确计算费舍尔信息矩阵（$\mathbf{F}$），但使用截断共轭梯度法（CG）近似求解 $\mathbf{F}^{-1} g$（即自然梯度），其中每一步CG迭代均采用高效的Hessian-向量积计算[Pea94]。该方法称为无Hessian优化（Hessian-free optimization）[Mar10a]，但其计算可能较慢，因为单次参数更新可能需要多次CG迭代。

6.4.5 指数族分布的自然梯度

本节，我们将假设 $\mathcal{L}$ 的形式为：

\[\mathcal{L}(\boldsymbol{\mu})=\mathbb{E}_{q_\mu(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] \tag{6.98}\]

其中$q_\mu(z)$是带有矩参数$\mu$的指数族分布。这是变分优化（补充材料第6.4.3节讨论）和自然进化策略（第6.7.6节讨论）的基础。

结果表明，关于矩参数的梯度与关于自然参数$\lambda$的自然梯度相同。这可由链式法则得出：

\[\frac{d}{d \boldsymbol{\lambda}} \mathcal{L}(\boldsymbol{\lambda})=\frac{d \boldsymbol{\mu}}{d \boldsymbol{\lambda}} \frac{d}{d \boldsymbol{\mu}} \mathcal{L}(\boldsymbol{\mu})=\mathbf{F}(\boldsymbol{\lambda}) \nabla_\mu \mathcal{L}(\boldsymbol{\mu}) \tag{6.99}\]

其中 $\mathcal{L}(\boldsymbol{\mu})=\mathcal{L}(\boldsymbol{\lambda}(\boldsymbol{\mu}))$，我们使用公式 （2.232）得到

\[\mathbf{F}(\boldsymbol{\lambda})=\nabla_\lambda \boldsymbol{\mu}(\boldsymbol{\lambda})=\nabla_\lambda^2 A(\boldsymbol{\lambda}) \tag{6.100}\]

所以

\[\bar{\nabla}_{\boldsymbol{\lambda}} \mathcal{L}(\boldsymbol{\lambda})=\mathbf{F}(\boldsymbol{\lambda})^{-1} \nabla_{\boldsymbol{\lambda}} \mathcal{L}(\boldsymbol{\lambda})=\nabla_\mu \mathcal{L}(\boldsymbol{\mu}) \tag{6.101}\]

接下来需要计算关于矩参数的（常规）梯度。具体计算方法将取决于$q$的形式和$L(\lambda)$的形式。我们将在下文讨论解决这个问题的几种方法。

6.4.5.1 Analytic computation for the Gaussian case

本节假设 $q(z) = \mathcal{N}(z|m, V)$， 我们将展示如何解析计算相关梯度。

根据第2.4.2.5节，$q$的自然参数为：

\[\boldsymbol{\lambda}^{(1)}=\mathbf{V}^{-1} \boldsymbol{m}, \boldsymbol{\lambda}^{(2)}=-\frac{1}{2} \mathbf{V}^{-1} \tag{6.102}\]

矩参数为

\[\boldsymbol{\mu}^{(1)}=\boldsymbol{m}, \boldsymbol{\mu}^{(2)}=\mathbf{V}+\boldsymbol{m} \boldsymbol{m}^{\top} \tag{6.103}\]

为简化推导，我们考虑标量情形。设$m = \mu^{(1)}$且$v = \mu^{(2)} - (\mu^{(1)})^2$。通过链式法则，关于矩参数的梯度可表示为：（其中$\mu^{(1)}$和$\mu^{(2)}$分别表示一阶和二阶矩参数）

\[\begin{align} & \frac{\partial \mathcal{L}}{\partial \mu^{(1)}}=\frac{\partial \mathcal{L}}{\partial m} \frac{\partial m}{\partial \mu^{(1)}}+\frac{\partial \mathcal{L}}{\partial v} \frac{\partial v}{\partial \mu^{(1)}}=\frac{\partial \mathcal{L}}{\partial m}-2 \frac{\partial \mathcal{L}}{\partial v} m \tag{6.104} \\ & \frac{\partial \mathcal{L}}{\partial \mu^{(2)}}=\frac{\partial \mathcal{L}}{\partial m} \frac{\partial m}{\partial \mu^{(2)}}+\frac{\partial \mathcal{L}}{\partial v} \frac{\partial v}{\partial \mu^{(2)}}=\frac{\partial \mathcal{L}}{\partial v} \tag{6.105} \end{align}\]

接下来需要计算关于$m$和$v$的导数。若$z \sim \mathcal{N}(m, V)$，根据Bonnet定理[Bon64]可得：（其中$m$表示均值参数，$v$表示方差参数）

\[\frac{\partial}{\partial m_i} \mathbb{E}[\tilde{\mathcal{L}}(\boldsymbol{z})]=\mathbb{E}\left[\frac{\partial}{\partial \theta_i} \tilde{\mathcal{L}}(\boldsymbol{z})\right] \tag{6.106}\]

根据 Price 定理，我们有

\[\frac{\partial}{\partial V_{i j}} \mathbb{E}[\tilde{\mathcal{L}}(\boldsymbol{z})]=c_{i j} \mathbb{E}\left[\frac{\partial^2}{\partial \theta_i \theta_j} \tilde{\mathcal{L}}(\boldsymbol{z})\right] \tag{6.107}\]

其中当$i=j$时$c_{ij}=\frac{1}{2}$，否则$c_{ij}=1$。（具体证明示例见gradient_expected_value_gaussian.ipynb文件）

在多变量情形下，结果可表示为[OA09; KR21a]：

\[\begin{align} \nabla_{\boldsymbol{\mu}^{(1)}} \mathbb{E}_{q(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] & =\nabla_{\boldsymbol{m}} \mathbb{E}_{q(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})]-2 \nabla_{\mathbf{V}} \mathbb{E}_{q(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] \boldsymbol{m} \tag{6.108}\\ & =\mathbb{E}_{q(\boldsymbol{z})}\left[\nabla_{\boldsymbol{z}} \tilde{\mathcal{L}}(\boldsymbol{z})\right]-\mathbb{E}_{q(\boldsymbol{z})}\left[\nabla_{\boldsymbol{z}}^2 \tilde{\mathcal{L}}(\boldsymbol{z})\right] \boldsymbol{m} \tag{6.109}\\ \nabla_{\boldsymbol{\mu}^{(z)}} \mathbb{E}_{q(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] & =\nabla_{\mathbf{V}} \mathbb{E}_{q(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] \tag{6.110}\\ & =\frac{1}{2} \mathbb{E}_{q(\boldsymbol{z})}\left[\nabla_{\boldsymbol{z}}^2 \tilde{\mathcal{L}}(\boldsymbol{z})\right] \tag{6.111} \end{align}\]

由此可见，自然梯度同时依赖于损失函数$\tilde{L}(z)$的梯度和Hessian矩阵。我们将在补充材料第6.4.2.2节看到这一结论的具体应用。（其中$\tilde{L}(z)$表示原始损失函数，Hessian矩阵为二阶导数矩阵）

6.4.5.2 Stochastic approximation for the general case

一般来说，解析计算自然梯度可能较为困难。不过，我们可以采用蒙特卡洛近似方法。为说明这点，假设$L$是如下形式的期望损失：

\[\mathcal{L}(\boldsymbol{\mu})=\mathbb{E}_{q_\mu(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] \tag{6.112}\]

根据式（6.101），自然梯度为

\[\nabla_\mu \mathcal{L}(\boldsymbol{\mu})=\mathbf{F}(\boldsymbol{\lambda})^{-1} \nabla_{\boldsymbol{\lambda}} \mathcal{L}(\boldsymbol{\lambda}) \tag{6.113}\]

对于指数族分布，等式右边的这两项都可以表示为期望形式，因此如[KL17a]所指出的，可以采用蒙特卡洛方法进行近似。具体来说，注意到：

\[\begin{align} \mathbf{F}(\boldsymbol{\lambda}) & =\nabla_\lambda \boldsymbol{\mu}(\boldsymbol{\lambda})=\nabla_{\boldsymbol{\lambda}} \mathbb{E}_{q_\lambda(z)}[\mathcal{T}(\boldsymbol{z})] \tag{6.114} \\ \nabla_{\boldsymbol{\lambda}} \mathcal{L}(\boldsymbol{\lambda}) & =\nabla_{\boldsymbol{\lambda}} \mathbb{E}_{q_{\boldsymbol{\lambda}}(\boldsymbol{z})}[\tilde{\mathcal{L}}(\boldsymbol{z})] \tag{6.115} \end{align}\]

若qq满足可重参数化条件，则可应用重参数化技巧（第6.3.5节）将梯度算子移入期望运算符内部。这使得我们能够：从 $q$ 中采样 $\boldsymbol{z}$，计算梯度后取平均，最终将得到的随机梯度传递给SGD算法。

6.4.5.3 能量函数的自然梯度

本节将讨论如何计算指数族分布熵的自然梯度，这在变分推断（第10章）中非常有用。该自然梯度的表达式为：

\[\tilde{\nabla}_{\boldsymbol{\lambda}} \mathbb{H}(\boldsymbol{\lambda})=-\nabla_\mu \mathbb{E}_{q_\mu(\boldsymbol{z})}[\log q(\boldsymbol{z})] \tag{6.116}\]

其中根据式（2.160），我们有

\[\log q(\boldsymbol{z})=\log h(\boldsymbol{z})+\mathcal{T}(\boldsymbol{z})^{\top} \boldsymbol{\lambda}-A(\boldsymbol{\lambda}) \tag{6.117}\]

考虑到 $\mathbb{E}[\mathcal{T}(\boldsymbol{z})]=\boldsymbol{\mu}$，我们有

\[\nabla_\mu \mathbb{E}_{q_\mu(\boldsymbol{z})}[\log q(\boldsymbol{z})]=\nabla_\mu \mathbb{E}_{q(\boldsymbol{z})}[\log h(\boldsymbol{z})]+\nabla_\mu \boldsymbol{\mu}^{\top} \boldsymbol{\lambda}(\boldsymbol{\mu})-\nabla_\mu A(\boldsymbol{\lambda}) \tag{6.118}\]

其中 $\boldsymbol{h}(\boldsymbol{z})$ 为 base measure。考虑到 $\boldsymbol{\lambda}$ 是关于 $\boldsymbol{\mu}$ 的函数，我们有

\[\nabla_\mu \mu^{\top} \boldsymbol{\lambda}=\boldsymbol{\lambda}+\left(\nabla_\mu \boldsymbol{\lambda}\right)^{\top} \boldsymbol{\mu}=\boldsymbol{\lambda}+\left(\mathbf{F}_\lambda^{-1} \nabla_{\boldsymbol{\lambda}} \boldsymbol{\lambda}\right)^{\top} \boldsymbol{\mu}=\boldsymbol{\lambda}+\mathbf{F}_\lambda^{-1} \boldsymbol{\mu} \tag{6.119}\]

因为 $\boldsymbol{\mu}=\nabla_{\boldsymbol{\lambda}} A(\boldsymbol{\lambda})$，我们有

\[\nabla_\mu A(\boldsymbol{\lambda})=\mathbf{F}_{\boldsymbol{\lambda}}^{-1} \nabla_{\boldsymbol{\lambda}} A(\boldsymbol{\lambda})=\mathbf{F}_{\boldsymbol{\lambda}}^{-1} \boldsymbol{\mu} \tag{6.120}\]

所以

\[-\nabla_\mu \mathbb{E}_{q_\mu(\boldsymbol{z})}[\log q(\boldsymbol{z})]=-\nabla_\mu \mathbb{E}_{q(\boldsymbol{z})}[\log h(\boldsymbol{z})]-\boldsymbol{\lambda} \tag{6.121}\]

如果假设 $h(\boldsymbol{z})=$ const，我们有

\[\bar{\nabla}_{\boldsymbol{\lambda}} \mathbb{H}(\boldsymbol{\lambda})=-\boldsymbol{\lambda} \tag{6.122}\]

6.5 确界优化（Bound optimization）算法

本节将讨论一类称为确界优化（bound optimization）或MM算法的算法。在最小化问题中，MM代表”Majorize-Minimize”（主要化-最小化）；在最大化问题中，MM则代表”Minorize-Maximize”（次要化-最大化）。MM算法包含许多实现，例如EM算法（第6.5.3节）、近端梯度法（第4.1节）、用于聚类的均值漂移算法[FH75; Che95; FT05]等。更多细节可参阅[HL04; Mai15; SBP17; Nad+19]等文献。

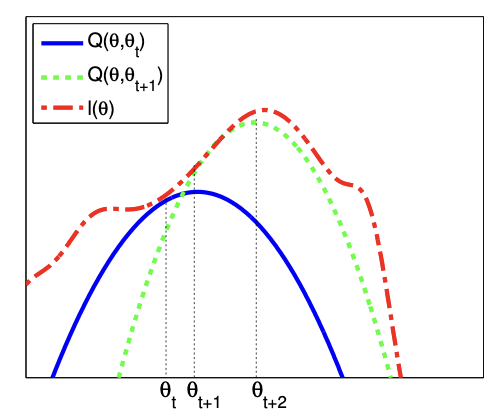
6.5.1 通用算法

在本节中，假设目标是最大化参数为 $\theta$ 的某个函数 $l(\theta)$。MM算法的核心思想是构造一个紧下界代理函数$Q(\theta, \theta^t)$，该函数满足：$Q(\theta, \theta^t) \leq l(\theta)$（下界条件）和$Q(\theta^t, \theta^t) = l(\theta^t)$（紧性条件）。当这些条件满足时，我们称 $Q$ 是 $l$ 的弱化函数（minorizes）。随后在每一步迭代中执行如下更新：

\[\boldsymbol{\theta}^{t+1}=\underset{\boldsymbol{\theta}}{\operatorname{argmax}} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^t\right) \tag{6.123}\]

这保证了原始目标函数的单调递增：

\[\ell\left(\boldsymbol{\theta}^{t+1}\right) \geq Q\left(\boldsymbol{\theta}^{t+1}, \boldsymbol{\theta}^t\right) \geq Q\left(\boldsymbol{\theta}^t, \boldsymbol{\theta}^t\right)=\ell\left(\boldsymbol{\theta}^t\right) \tag{6.124}\]

其中，第一个不等式成立是因为对于任意$\theta’$，$Q(\theta^t, \theta’)$ 是 $l(\theta^t)$ 的下界；第二个不等式由式（6.123）保证；最后的等式则源于紧性条件的约束。这一结果的直接推论是：如果目标函数未呈现单调上升趋势，则必然在数学推导和/或代码实现中存在错误——这一性质可成为极其强大的调试工具。

该过程的示意图见图6.7。红色虚线表示原始函数（例如观测数据的对数似然）； 蓝色实线表示在 $\theta^t$ 处计算的下界函数，该函数在 $\theta^t$ 点与目标函数相切； 我们将 $\theta^{t+1}$ 设为该下界函数（蓝色曲线）的最大值所在点，并在该点拟合新的下界（绿色虚线）； 新下界函数的最优解即作为 $\theta^{t+2}$，依此类推。

6.5.2 案例：逻辑回归

如果要最大化的目标函数 $l(\theta)$ 是凹函数（开口向下），那么构造有效下界的一种方法是对其Hessian矩阵进行约束，即找到一个负定矩阵$\mathbf{B}$，使得$\mathbf{H}(\theta) \succ \mathbf{B}$。此时可以证明（参见[BCN18, 附录B]）：

\[\ell(\boldsymbol{\theta}) \geq \ell\left(\boldsymbol{\theta}^t\right)+\left(\boldsymbol{\theta}-\boldsymbol{\theta}^t\right)^{\top} \boldsymbol{g}\left(\boldsymbol{\theta}^t\right)+\frac{1}{2}\left(\boldsymbol{\theta}-\boldsymbol{\theta}^t\right)^{\top} \mathbf{B}\left(\boldsymbol{\theta}-\boldsymbol{\theta}^t\right) \tag{6.125}\]

其中 $\boldsymbol{g}\left(\boldsymbol{\theta}^t\right)=\nabla \ell\left(\boldsymbol{\theta}^t\right)$。所以下面的函数是一个有效的下确界：

\[Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^t\right)=\boldsymbol{\theta}^{\top}\left(\boldsymbol{g}\left(\boldsymbol{\theta}^t\right)-\mathbf{B} \boldsymbol{\theta}^t\right)+\frac{1}{2} \boldsymbol{\theta}^{\top} \mathbf{B} \boldsymbol{\theta} \tag{6.126}\]

对应的参数更新规则为：

\[\boldsymbol{\theta}^{t+1}=\boldsymbol{\theta}^t-\mathbf{B}^{-1} \boldsymbol{g}\left(\boldsymbol{\theta}^t\right) \tag{6.127}\]

这类似于牛顿法更新，但区别在于我们使用一个固定的矩阵$\mathbf{B}$，而不是每次迭代都变化的$\mathbf{H}(\theta^t)$。这样可以在较低计算成本下获得二阶方法的部分优势。

例如，我们使用MM算法来拟合一个多类逻辑回归模型。（这里采用[Kri+05]的表述，该文献还讨论了更复杂的稀疏逻辑回归情况。）样本$n$属于类别$c \in {1, \dots, C}$的概率为：

\[p\left(y_n=c \mid \boldsymbol{x}_n, \boldsymbol{w}\right)=\frac{\exp \left(\boldsymbol{w}_c^{\top} \boldsymbol{x}_n\right)}{\sum_{i=1}^C \exp \left(\boldsymbol{w}_i^{\top} \boldsymbol{x}_n\right)} \tag{6.128}\]

由于归一化条件 $\sum_{c=1}^C p(y_n=c|\mathbf{x}_n, \mathbf{w}) = 1$， 我们可以设 $\mathbf{w}_C = \mathbf{0}$。 （例如在二分类逻辑回归中，$C=2$，此时仅需学习一个权重向量。）因此，参数 $\theta$ 对应于一个大小为 $D \times (C-1)$ 的权重矩阵 $\mathbf{w}$， 其中 $\mathbf{x}_n \in \mathbb{R}^D$。

如果我们令 $\mathbf{p}_n(\mathbf{w}) = [p(y_n=1|\mathbf{x}_n, \mathbf{w}), \dots, p(y_n=C-1|\mathbf{x}_n, \mathbf{w})]$ 且 $\mathbf{y}_n = [\mathbb{I}(y_n=1), \dots, \mathbb{I}(y_n=C-1)]$， 则对数似然函数可表示为：

\[\ell(\boldsymbol{w})=\sum_{n=1}^N\left[\sum_{c=1}^{C-1} y_{n c} \boldsymbol{w}_c^{\top} \boldsymbol{x}_n-\log \sum_{c=1}^C \exp \left(\boldsymbol{w}_c^{\top} \boldsymbol{x}_n\right)\right] \tag{6.129}\]

梯度为：

\[\boldsymbol{g}(\boldsymbol{w})=\sum_{n=1}^N\left(\boldsymbol{y}_n-\boldsymbol{p}_n(\boldsymbol{w})\right) \otimes \boldsymbol{x}_n \tag{6.130}\]

其中$\otimes$表示Kronecker积（在此情境下即为两个向量的外积）。 Hessian矩阵由下式给出：

\[\mathbf{H}(\boldsymbol{w})=-\sum_{n=1}^N\left(\operatorname{diag}\left(\boldsymbol{p}_n(\boldsymbol{w})\right)-\boldsymbol{p}_n(\boldsymbol{w}) \boldsymbol{p}_n(\boldsymbol{w})^{\top}\right) \otimes\left(\boldsymbol{x}_n \boldsymbol{x}_n^{\top}\right) \tag{6.131}\]

我们可以如[Boh92]所示，构造Hessian矩阵的一个下界：

\[\mathbf{H}(\boldsymbol{w}) \succ-\frac{1}{2}\left[\mathbf{I}-\mathbf{1 1}^{\top} / C\right] \otimes\left(\sum_{n=1}^N \boldsymbol{x}_n \boldsymbol{x}_n^{\top}\right) \triangleq \mathbf{B} \tag{6.132}\]

其中 $\mathbf{I}$ 是 $(C-1)$ 维单位矩阵，$\mathbf{1}$ 是$(C-1)$维全1向量。对于二分类情况（$C=2$），该表达式简化为：

\[\mathbf{H}(\boldsymbol{w}) \succ-\frac{1}{2}\left(1-\frac{1}{2}\right)\left(\sum_{n=1}^N \boldsymbol{x}_n^{\top} \boldsymbol{x}_n\right)=-\frac{1}{4} \mathbf{X}^{\top} \mathbf{X} \tag{6.133}\]

这是因为$p_n \leq 0.5$，所以$-(p_n - p_n^2) \geq -0.25$。

我们可以利用这个下界来构建一个MM算法以寻找最大似然估计(MLE)。此时参数更新公式变为：

\[\boldsymbol{w}^{t+1}=\boldsymbol{w}^t-\mathbf{B}^{-1} \boldsymbol{g}\left(\boldsymbol{w}^t\right) \tag{6.134}\]

例如，考虑二分类情况，此时梯度 $\mathbf{g}^t = \nabla l(\mathbf{w}^t) = \mathbf{X}^\top (\mathbf{y} - \boldsymbol{\mu}^t)$，其中 $\boldsymbol{\mu}^t = [p_n(\mathbf{w}^t), (1 - p_n(\mathbf{w}^t))]_{n=1}^N$。更新公式转化为：

\[\boldsymbol{w}^{t+1}=\boldsymbol{w}^t-4\left(\mathbf{X}^{\top} \mathbf{X}\right)^{-1} \boldsymbol{g}^t \tag{6.135}\]

上述方法在每一步的计算速度上快于IRLS算法（迭代加权最小二乘法，即牛顿法）——后者是拟合广义线性模型（GLM）的标准方法。原因在于：牛顿法的更新形式为

\[\boldsymbol{w}^{t+1}=\boldsymbol{w}^t-\mathbf{H}^{-1} \boldsymbol{g}\left(\boldsymbol{w}^t\right)=\boldsymbol{w}^t-\left(\mathbf{X}^{\top} \mathbf{S}^t \mathbf{X}\right)^{-1} \boldsymbol{g}^t \tag{6.136}\]

其中 $\mathbf{S}^t = \text{diag}(\boldsymbol{\mu}^t \odot (1 - \boldsymbol{\mu}^t))$。显然，式(6.135)的计算效率更高，因为我们可以预先计算并存储常数矩阵$(\mathbf{X}^\top\mathbf{X})^{-1}$。 （注：这里$\odot$表示逐元素乘法，MM算法通过避免每次迭代重新计算和求逆权重矩阵$\mathbf{S}^t$，实现了比IRLS更快的单步计算速度，尤其在大规模数据下优势显著。）

6.5.3 EM算法

本节将讨论期望最大化（EM）算法[DLR77; MK07]。该算法专门用于优化一类概率模型的参数，该类模型的特点在于训练数据中存在 缺失项 和/或 隐变量。EM算法是MM算法的一个特例。

EM算法的核心思想是交替执行两个步骤：E步（求解期望）——估计隐变量（或缺失值），计算完整数据下对数似然函数的期望；M步（最大化）——基于完整数据计算参数的最大似然估计。由于计算期望依赖于参数的估计，而参数的估计又依赖于期望的计算，因此需要迭代执行这一过程。

在6.5.3.1节中，我们将证明EM算法是一种界优化算法，这意味着该迭代过程将收敛到对数似然函数的局部最大值。收敛速度受缺失数据的规模影响，它会影响确界的紧致性[XJ96; MD97; SRG03; KKS20]。

接下来我们将介绍一般意义下的EM算法。设 $y_n$ 表示第$n$个样本的观测数据，$z_n$ 为对应的隐变量。

（注：EM算法的优势在于通过引入隐变量的期望，将复杂的 边缘似然最大化问题 转化为可迭代优化的完整数据似然 问题，广泛应用于混合模型、隐马尔可夫模型等场景。）

6.5.3.1 下确界

EM 算法的优化目标是最大化观测数据的对数似然：

\[\ell(\boldsymbol{\theta})=\sum_{n=1}^N \log p\left(\boldsymbol{y}_n \mid \boldsymbol{\theta}\right)=\sum_{n=1}^N \log \left[\sum_{\boldsymbol{z}_n} p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)\right] \tag{6.137}\]

其中 $\boldsymbol{y}_n$ 表示观测变量，$\boldsymbol{z}_n$ 表示隐变量。问题在于，由于对数操作不能置于求和操作内部，上式的优化变得很难。EM 算法绕开了这一难点。首先，考虑一组关于每个隐变量 $\boldsymbol{z}_n$ 的任意概率分布 $q_n(\boldsymbol{z}_n)$。此时，式（6.137）可以写成：

\[\ell(\boldsymbol{\theta})=\sum_{n=1}^N \log \left[\sum_{\boldsymbol{z}_n} q_n\left(\boldsymbol{z}_n\right) \frac{p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)}{q_n\left(\boldsymbol{z}_n\right)}\right] \tag{6.138}\]

基于琴森不等式，可以将对数操作置于期望（求和）操作的内部，从而得到对数似然的下确界：

\[\begin{align} \ell(\boldsymbol{\theta}) & \geq \sum_n \sum_{\boldsymbol{z}_n} q_n\left(\boldsymbol{z}_n\right) \log \frac{p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)}{q_n\left(\boldsymbol{z}_n\right)} \tag{6.139}\\ & =\sum_n \underbrace{\mathbb{E}_{q_n}\left[\log p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)\right]+\mathbb{H}\left(q_n\right)}_{\mathrm{Ł}\left(\boldsymbol{\theta}, q_n \mid \boldsymbol{y}_n\right)} \tag{6.140}\\ & =\sum_n \mathrm{Ł}\left(\boldsymbol{\theta}, q_n \mid \boldsymbol{y}_n\right) \triangleq \mathrm{Ł}\left(\boldsymbol{\theta},\left\{q_n\right\} \mid \mathcal{D}\right) \tag{6.141} \end{align}\]

其中 $\mathbb{H}(q)$ 表示分布 $q$ 的熵，$\mathrm{Ł}(\boldsymbol{\theta},{q_n} \mid \mathcal{D})$ 被称为 证据下确界（evidence lower bound，ELBO），因为它是对数边际似然 $\log p(\boldsymbol{y}_{1: N} \mid \boldsymbol{\theta})$ 的下确界，该对数似然又被称为证据。优化上述边际似然是变分推断的基础，我们将在10.1节进行讨论。

6.5.3.2 E step

我们发现下确界实际上是 $N$ 项求和的结果，其中的每一项定义为：

\[\begin{align} \mathrm{Ł}\left(\boldsymbol{\theta}, q_n \mid \boldsymbol{y}_n\right) & =\sum_{\boldsymbol{z}_n} q_n\left(\boldsymbol{z}_n\right) \log \frac{p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)}{q_n\left(\boldsymbol{z}_n\right)} \tag{6.142}\\ & =\sum_{\boldsymbol{z}_n} q_n\left(\boldsymbol{z}_n\right) \log \frac{p\left(\boldsymbol{z}_n \mid \boldsymbol{y}_n, \boldsymbol{\theta}\right) p\left(\boldsymbol{y}_n \mid \boldsymbol{\theta}\right)}{q_n\left(\boldsymbol{z}_n\right)} \tag{6.143}\\ & =\sum_{\boldsymbol{z}_n} q_n\left(\boldsymbol{z}_n\right) \log \frac{p\left(\boldsymbol{z}_n \mid \boldsymbol{y}_n, \boldsymbol{\theta}\right)}{q_n\left(\boldsymbol{z}_n\right)}+\sum_{\boldsymbol{z}_n} q_n\left(\boldsymbol{z}_n\right) \log p\left(\boldsymbol{y}_n \mid \boldsymbol{\theta}\right) \tag{6.144}\\ & =-D_{\mathbb{KL}}\left(q_n\left(\boldsymbol{z}_n\right) \| p\left(\boldsymbol{z}_n \mid \boldsymbol{y}_n, \boldsymbol{\theta}\right)\right)+\log p\left(\boldsymbol{y}_n \mid \boldsymbol{\theta}\right) \tag{6.145} \end{align}\]

其中 $D_{\mathbb{KL}}(q | p) \triangleq \sum_z q(z) \log \frac{q(z)}{p(z)}$ 表示KL 散度。我们在5.1节讨论了关于KL散度的更多细节，但核心的一点是 $D_{\mathbb{KL}}(q | p) \geq 0$，且 $D_{\mathbb{KL}}(q | p)=0$ 的充要条件是 $q=p$。所以在关于 ${q_n}$ 优化下确界 $\mathrm{Ł}(\boldsymbol{\theta},{q_n} \mid \mathcal{D})$ 的阶段，可以令每一个分布 $q_n^*=p(\boldsymbol{z}_n \mid \boldsymbol{y}_n, \boldsymbol{\theta})$，这被称为 E step。这将确保 ELBO 是一个紧凑的下确界：

\[\mathrm{Ł}\left(\boldsymbol{\theta},\left\{q_n^*\right\} \mid \mathcal{D}\right)=\sum_n \log p\left(\boldsymbol{y}_n \mid \boldsymbol{\theta}\right)=\ell(\boldsymbol{\theta} \mid \mathcal{D}) \tag{6.146}\]

为了说明EM算法为什么属于界优化，定义

\[Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^t\right)=\mathrm{Ł}\left(\boldsymbol{\theta},\left\{p\left(\boldsymbol{z}_n \mid \boldsymbol{y}_n ; \boldsymbol{\theta}^t\right)\right\}\right) \tag{6.147}\]

接下来，我们有 $Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^t\right) \leq \ell(\boldsymbol{\theta})$， 并且 $Q\left(\boldsymbol{\theta}^t, \boldsymbol{\theta}^t\right)=\ell\left(\boldsymbol{\theta}^t\right)$。

然而，如果无法精确计算后验概率 $p(\boldsymbol{z}_n|\boldsymbol{y}_n; \boldsymbol{\theta}^t)$， 仍可采用近似分布 $q\left(\boldsymbol{z}_n \mid \boldsymbol{y}_n ; \boldsymbol{\theta}^t\right)$， 这将产生对数似然的一个非紧致下界。这种推广版本的EM算法被称为变分EM[NH98b]，详见章节6.5.6.1。

6.5.3.3 M step

在 M 步中，我们需要关于参数 $\boldsymbol{\theta}$ 最大化 $\mathrm{Ł}(\boldsymbol{\theta}, {q_{t,n}})$，其中 $q_{t,n}$ 是第 $t$ 次迭代的 E 步中计算得到的分布。由于熵 $\mathbb{H}(q_n)$ 关于 $\boldsymbol{\theta}$ 是常数，在 M 步中将其忽略，最终只需优化：

\[\ell^t(\boldsymbol{\theta})=\sum_n \mathbb{E}_{q_n^t\left(\boldsymbol{z}_n\right)}\left[\log p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)\right] \tag{6.148}\]

这被称为完全数据对数似然期望（expected complete data log likelihood）。如果联合概率分布属于指数族（第 2.4 节），该式可以改写为：

\[\ell^t(\boldsymbol{\theta})=\sum_n \mathbb{E}\left[\mathcal{T}\left(\boldsymbol{y}_n, \boldsymbol{z}_n\right)^{\top} \boldsymbol{\theta}-A(\boldsymbol{\theta})\right]=\sum_n\left(\mathbb{E}\left[\mathcal{T}\left(\boldsymbol{y}_n, \boldsymbol{z}_n\right)\right]^{\top} \boldsymbol{\theta}-A(\boldsymbol{\theta})\right) \tag{6.149}\]

其中 $\mathbb{E}\left[\mathcal{T}\left(\boldsymbol{y}_n, \boldsymbol{z}_n\right)\right]$ 称为充分统计量期望（expected sufficient statistics）。

在 M 步中，我们通过最大化完全数据对数似然期望（expected complete data log likelihood）来得到新的参数估计：

\[\boldsymbol{\theta}^{t+1}=\arg \max _{\boldsymbol{\theta}} \sum_n \mathbb{E}_{q_n^t}\left[\log p\left(\boldsymbol{y}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right)\right] \tag{6.150}\]

在指数族分布的情况下，可以通过充分统计量期望矩匹配（moment matching of the expected sufficient statistics）（第 2.4.5 节）得到参数的闭式解。

从上述分析可以看出，E 步实际上并不需要返回完整的后验分布集合 \(\{q(\boldsymbol{z}_n)\}\)， 而只需返回充分统计量的期望值的总和 \(\sum_n \mathbb{E}_{q(z_n)}[\mathcal{T}\left(\boldsymbol{y}_n, \boldsymbol{z}_n\right)]\)。

EM 算法的一个典型应用是拟合混合模型（mixture models），我们在本书的基础版 [Mur22] 中已讨论过。接下来，我们将给出一个不同的示例。

6.5.4 案例：EM 算法用于缺失数据的MVN

通常情况下，如果我们有一个完全观测的数据矩阵，则可以很容易地计算出多变量正态分布的MLE——只需要计算样本的均值和方差。本节，我们将考虑一种情况，即数据矩阵中存在缺失值（missing data）或部分观测数据（partially observed data）。举个例子，考虑 $\mathbf{Y}$ 为一个调研的答案；而其中某些答案是未知的。第3.11节介绍了很多类型的缺失数据。本节，为便于分析，我们使用随机缺失（missing at random, MAR）假设。基于MAR假设，观测数据的对数似然定义为：

\[\log p(\mathbf{X} \mid \boldsymbol{\theta})=\sum_n \log p\left(\boldsymbol{x}_n \mid \boldsymbol{\theta}\right)=\sum_n \log \left[\int p\left(\boldsymbol{x}_n, \boldsymbol{z}_n \mid \boldsymbol{\theta}\right) d \boldsymbol{z}_n\right] \tag{6.151}\]

其中 $\boldsymbol{x}_n$ 表示样本 $n$ 的可见变量， $\boldsymbol{z}_n$ 表示隐变量，$\boldsymbol{y}_n=(\boldsymbol{z}_n,\boldsymbol{x}_n)$ 表示完整的随机变量。遗憾的是，这一目标函数难以直接最大化，因为我们无法将对数运算移入期望运算。不过我们可以轻松应用期望最大化（EM）算法来解决这一问题。

6.5.4.1 E步骤

假设已有上一迭代步骤的参数 $\boldsymbol{\theta}^{t-1}$。接着我们计算在 $t$ 步骤的完全数据的对数似然的期望：

\[\begin{align} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{t-1}\right) & =\mathbb{E}\left[\sum_{n=1}^N \log \mathcal{N}\left(\boldsymbol{y}_n \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}\right) \mid \mathcal{D}, \boldsymbol{\theta}^{t-1}\right] \tag{6.152}\\ & =-\frac{N}{2} \log |2 \pi \boldsymbol{\Sigma}|-\frac{1}{2} \sum_n \mathbb{E}\left[\left(\boldsymbol{y}_n-\boldsymbol{\mu}\right)^{\top} \boldsymbol{\Sigma}^{-1}\left(\boldsymbol{y}_n-\boldsymbol{\mu}\right)\right] \tag{6.153}\\ & =-\frac{N}{2} \log |2 \pi \boldsymbol{\Sigma}|-\frac{1}{2} \operatorname{tr}\left(\boldsymbol{\Sigma}^{-1} \sum_n \mathbb{E}\left[\left(\boldsymbol{y}_n-\boldsymbol{\mu}\right)\left(\boldsymbol{y}_n-\boldsymbol{\mu}\right)^{\top}\right]\right. \tag{6.154}\\ & =-\frac{N}{2} \log |\boldsymbol{\Sigma}|-\frac{N D}{2} \log (2 \pi)-\frac{1}{2} \operatorname{tr}\left(\boldsymbol{\Sigma}^{-1} \mathbb{E}[\mathbf{S}(\boldsymbol{\mu})]\right) \tag{6.155} \end{align}\]

其中

\[\mathbb{E}[\mathbf{S}(\boldsymbol{\mu})] \triangleq \sum_n\left(\mathbb{E}\left[\boldsymbol{y}_n \boldsymbol{y}_n^{\top}\right]+\boldsymbol{\mu} \boldsymbol{\mu}^{\top}-2 \boldsymbol{\mu} \mathbb{E}\left[\boldsymbol{y}_n\right]^{\top}\right) \tag{6.156}\]

（为简洁起见，我们省略了条件项 $D$ 和 $\theta^{t-1}$。）可以看出，我们需要计算 $\sum_n \mathbb{E}[\boldsymbol{y}_n]$ 和 $\sum_n \mathbb{E}[\boldsymbol{y}_n \boldsymbol{y}_n^{\top}]$，即充分统计量期望（expected sufficient statistics）。

为了计算这些统计量，利用第2.3.1.3节中的结论：

\[\begin{align} & p\left(\boldsymbol{z}_n \mid \boldsymbol{x}_n, \boldsymbol{\theta}\right)=\mathcal{N}\left(\boldsymbol{z}_n \mid \boldsymbol{m}_n, \mathbf{V}_n\right) \tag{6.157}\\ & \boldsymbol{m}_n \triangleq \boldsymbol{\mu}_h+\boldsymbol{\Sigma}_{h v} \boldsymbol{\Sigma}_{v v}^{-1}\left(\boldsymbol{x}_n-\boldsymbol{\mu}_v\right) \tag{6.158}\\ & \mathbf{V}_n \triangleq \boldsymbol{\Sigma}_{h h}-\boldsymbol{\Sigma}_{h v} \boldsymbol{\Sigma}_{v v}^{-1} \boldsymbol{\Sigma}_{v h} \tag{6.159} \end{align}\]

其中，我们将均值 $\boldsymbol{\mu}$ 和协方差矩阵 $\boldsymbol{\Sigma}$ 按照隐变量索引 $h$ 和观测变量索引 $v$ 进行分块处理。因此，充分统计量的期望为：

\[\mathbb{E}\left[\boldsymbol{y}_n\right]=\left(\mathbb{E}\left[\boldsymbol{z}_n\right] ; \boldsymbol{x}_n\right)=\left(\boldsymbol{m}_n ; \boldsymbol{x}_n\right) \tag{6.160}\]

为了计算 $\mathbb{E}[\boldsymbol{y}_n \boldsymbol{y}_n^\top]$，利用协方差公式 $\operatorname{Cov}[\boldsymbol{y}]=\mathbb{E}\left[\boldsymbol{y} \boldsymbol{y}^{\top}\right]-\mathbb{E}[\boldsymbol{y}] \mathbb{E}\left[\boldsymbol{y}^{\top}\right]$，得到：

\[\begin{align} & \mathbb{E}\left[\boldsymbol{y}_n \boldsymbol{y}_n^{\top}\right]=\mathbb{E}\left[\binom{\boldsymbol{z}_n}{\boldsymbol{x}_n}\left(\begin{array}{ll} \boldsymbol{z}_n^{\top} & \boldsymbol{x}_n^{\top} \end{array}\right)\right]=\left(\begin{array}{cc} \mathbb{E}\left[\boldsymbol{z}_n \boldsymbol{z}_n^{\top}\right] & \mathbb{E}\left[\boldsymbol{z}_n\right] \boldsymbol{x}_n^{\top} \tag{6.161}\\ \boldsymbol{x}_n \mathbb{E}\left[\boldsymbol{z}_n\right]^{\top} & \boldsymbol{x}_n \boldsymbol{x}_n^{\top} \end{array}\right) \\ & \mathbb{E}\left[\boldsymbol{z}_n \boldsymbol{z}_n^{\top}\right]=\mathbb{E}\left[\boldsymbol{z}_n\right] \mathbb{E}\left[\boldsymbol{z}_n\right]^{\top}+\mathbf{V}_n \tag{6.162} \end{align}\]

6.5.4.2 M 步骤

通过求解 $\nabla Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t-1)}\right)=\mathbf{0}$ 可以证明，M步等价于将这些充分统计量期望（ESS）代入标准的最大似然估计（MLE）方程，从而得到参数更新：

\[\begin{align} \boldsymbol{\mu}^t & =\frac{1}{N} \sum_n \mathbb{E}\left[\boldsymbol{y}_n\right] \tag{6.163}\\ \boldsymbol{\Sigma}^t & =\frac{1}{N} \sum_n \mathbb{E}\left[\boldsymbol{y}_n \boldsymbol{y}_n^{\top}\right]-\boldsymbol{\mu}^t\left(\boldsymbol{\mu}^t\right)^{\top} \tag{6.164} \end{align}\]

由此可见，EM算法并不等同于简单地将变量替换为其期望值后直接套用标准最大似然估计（MLE）公式——这种做法会忽略后验方差，导致估计结果有误。实际上，我们必须计算充分统计量的期望值，并将其代入常规的MLE方程中进行求解。

6.5.4.3 初始化

为了启动算法，我们可以基于数据矩阵中那些完全观测到的行来计算最大似然估计（MLE）。如果不存在这样的行，我们可以仅利用观测到的边缘统计量来估计协方差矩阵 $\boldsymbol{\Sigma}$ 的对角项。之后，我们就可以开始运行EM算法。

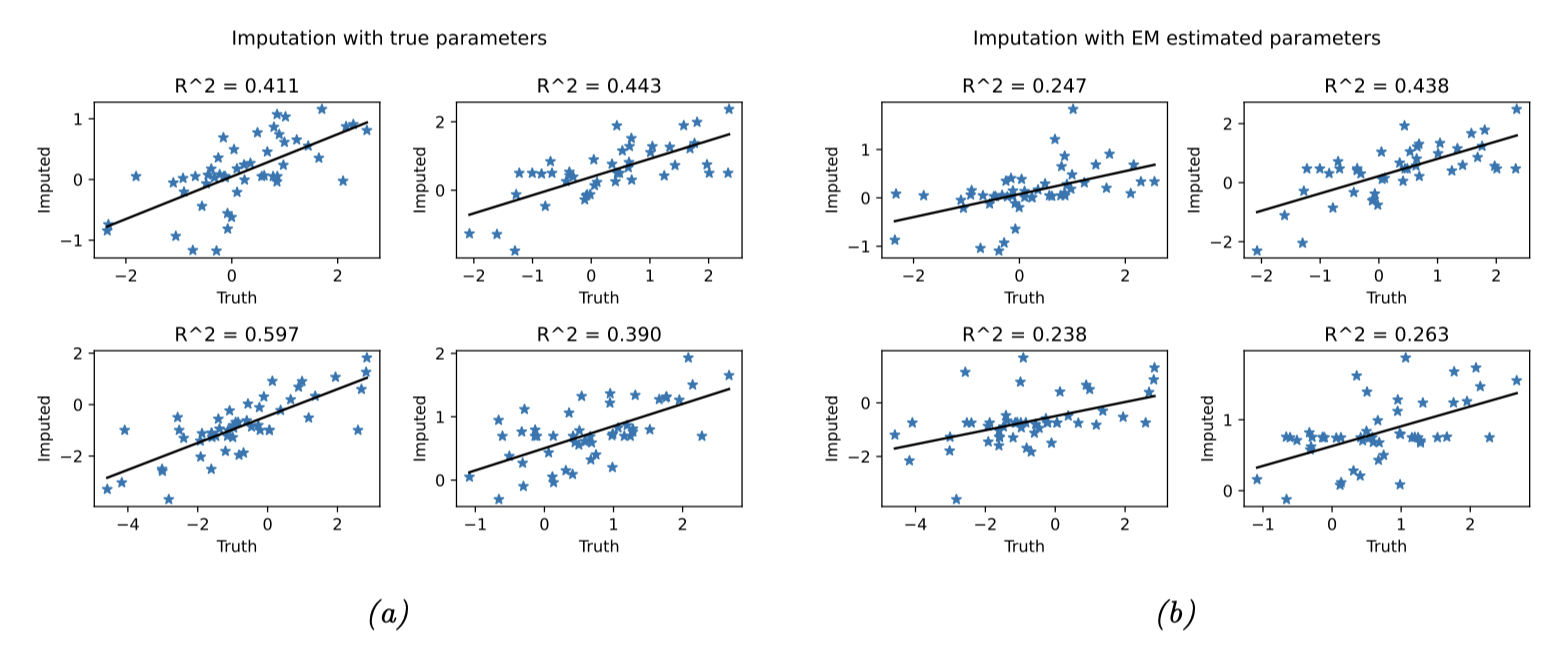
6.5.4.4 案例

我们通过一个缺失值填补（imputation）的问题来说明整个过程：假设现有 $N=100$ 个 10 维数据点（假设服从高斯分布），其中 50% 的观测值随机缺失。 首先采用 EM 算法估计参数，记所得参数为 $\hat{\boldsymbol{\theta}}$。 基于训练好的模型，可通过计算条件期望 $\mathbb{E}[\boldsymbol{z}_n \mid \boldsymbol{x}_n, \hat{\boldsymbol{\theta}}]$ 进行缺失值预测。 如图 6.8 所示，使用 $\hat{\boldsymbol{\theta}}$ 得到的结果与真实参数的效果几乎一致。 整个优化性能随数据量的增加或缺失值比例的降低而提升（这一结论符合预期）。

6.5.5 案例：使用 Student 似然实现鲁棒线性回归

本节将讨论如何利用EM算法拟合基于学生t分布（而非传统高斯分布）的线性回归模型，以增强模型的鲁棒性。该方法最初由[Zel76]提出，其似然函数定义为：

\[p\left(y \mid \boldsymbol{x}, \boldsymbol{w}, \sigma^2, \nu\right)=\mathcal{T}\left(y \mid \boldsymbol{w}^{\top} \boldsymbol{x}, \sigma^2, \nu\right) \tag{6.165}\]

乍看之下，这个问题似乎无从下手，因为既没有缺失数据，也不存在隐变量。然而，我们可以通过引入“人工”隐变量来简化问题——这是一种常见技巧。关键在于，我们可以如第28.2.3.1节所述，将学生t分布表示为高斯尺度混合(GSM)。

具体到当前问题，我们为每个样本关联一个隐变量尺度参数$z_n \in \mathbb{R}^+$，此时完全数据的对数似然函数为：

\[\begin{align} \log p\left(\boldsymbol{y}, \boldsymbol{z} \mid \mathbf{X}, \boldsymbol{w}, \sigma^2, \nu\right) & =\sum_n-\frac{1}{2} \log \left(2 \pi z_n \sigma^2\right)-\frac{1}{2 z_n \sigma^2}\left(y_i-\boldsymbol{w}^T \boldsymbol{x}_i\right)^2 \tag{6.166}\\ & +\left(\frac{\nu}{2}-1\right) \log \left(z_n\right)-z_n \frac{\nu}{2}+\mathrm{const} \tag{6.167} \end{align}\]

忽略与参数 $\boldsymbol{w}$ 无关的项并取期望后，可得：

\[Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}^t\right)=-\sum_n \frac{\lambda_n}{2 \sigma^2}\left(y_n-\boldsymbol{w}^T \boldsymbol{x}_n\right)^2 \tag{6.168}\]

其中 $\lambda_n^{(t)} \triangleq \mathbb{E}[1/z_n | y_n, \boldsymbol{x}_n, \boldsymbol{w}^{(t)}]$。 可以看出，这实际上是一个加权最小二乘问题，每个数据点的权重为 $\lambda_n^{(t)}$。

接下来我们讨论如何计算这些权重。利用第2.2.3.4节的结果可以证明：

\[p\left(z_n \mid y_n, \boldsymbol{x}_n, \boldsymbol{\theta}\right)=\mathrm{IG}\left(\frac{\nu+1}{2}, \frac{\nu+\delta_n}{2}\right) \tag{6.169}\]

其中 $\delta_n=\frac{\left(y_n-x^T x_n\right)^2}{\sigma^2}$ 为标准化后的残差。所以

\[\lambda_n=\mathbb{E}\left[1 / z_n\right]=\frac{\nu^t+1}{\nu^t+\delta_n^t} \tag{6.170}\]

因此，当残差 $\delta_n^{(t)}$ 较大时，该数据点将被赋予较小的权重 $\lambda_n^{(t)}$ —— 这一机制具有直观的解释性，因为这类数据点很可能是离群值（outlier）。

6.5.6 EM的扩展

EM算法存在诸多变体与扩展形式，如[MK97]所述。以下简要总结其中几种主要方法。

6.5.6.1 变分 EM

在 E 步中，我们选择 \(q_n^*=\operatorname{argmin}_{q_n \in \mathcal{Q}} D_{\mathbb{K L}}\left(q_n \| p\left(\boldsymbol{z}_n \mid \boldsymbol{x}_n, \boldsymbol{\theta}\right)\right)\)。 由于是在函数空间中进行优化，这被称为变分推断（详见第 10.1 节）。如果分布族 $\mathcal{Q}$ 足够丰富，能够包含真实后验 \(q_n=p\left(\boldsymbol{z}_n \mid \boldsymbol{x}_n, \boldsymbol{\theta}\right)\)， 那么我们可以使 KL 散度为零。但通常出于计算复杂度考虑，我们可能会选择更受限的分布类。例如，即使真实后验的变量之间是相关的，我们仍可能使用 \(q_n\left(\boldsymbol{z}_n\right)=\mathcal{N}\left(\boldsymbol{z}_n \mid \boldsymbol{\mu}_n, \operatorname{diag}\left(\boldsymbol{\sigma}_n\right)\right)\)。

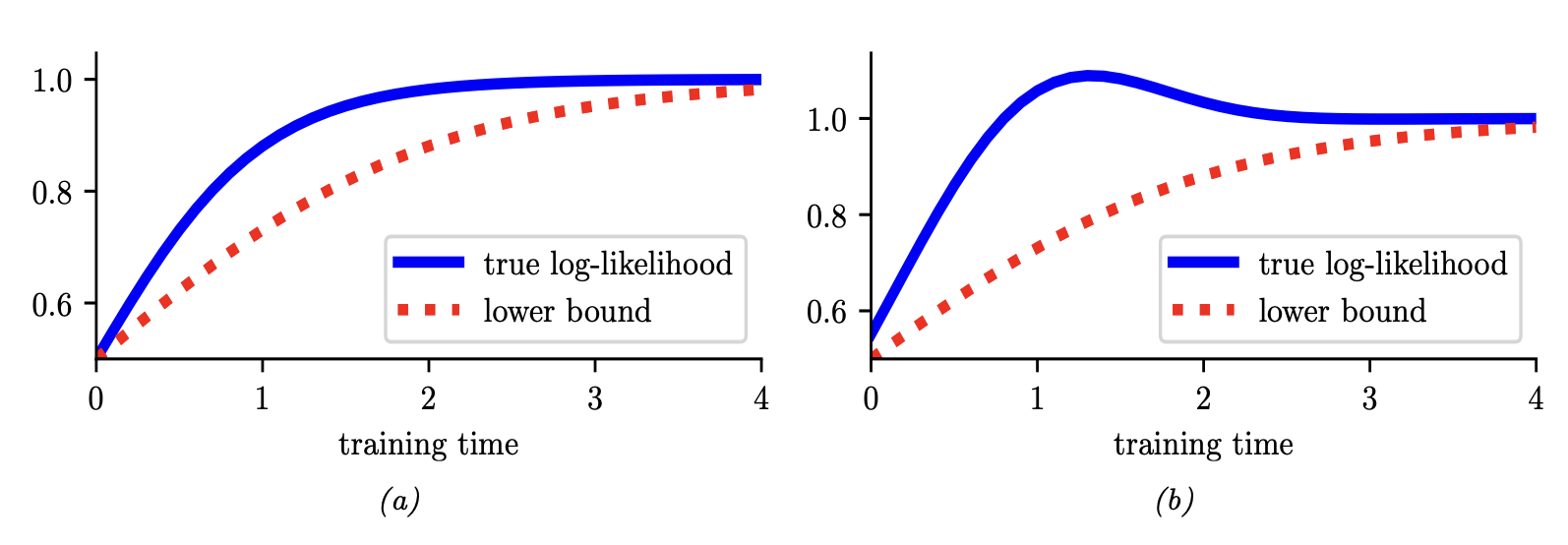
在 EM 的 E 步中使用受限后验分布族 $\mathcal{Q}$ 的方法称为变分 EM [NH98a]。与常规 EM 不同，变分 EM 并不能保证实际对数似然本身会增加（见图 6.9），但它确实能单调地提高变分下界。我们可以通过改变变分族 $\mathcal{Q}$ 来控制该下界的贴合度；当 $q_n = p_n$（对应于精确推断）时，我们就恢复了与常规 EM 相同的行为。更多讨论见第 10.1.3 节。

6.5.6.2 Hard EM

假设我们在变分EM中使用退化的后验近似，即点估计 \(q\left(\boldsymbol{z} \mid \boldsymbol{x}_n\right)=\delta_{\hat{\boldsymbol{z}}_n}(\boldsymbol{z})\)， 其中 \(\hat{\boldsymbol{z}}_n=\operatorname{argmax}_{\boldsymbol{z}} p\left(\boldsymbol{z} \mid \boldsymbol{x}_n\right)\)。 这等价于hard EM，即在E步中忽略 $\boldsymbol{z}_n$ 的不确定性。

这种退化方法的问题在于它极易过拟合，因为隐变量的数量与数据集的数量成正比[WCS08]。

6.5.6.3 蒙特卡洛 EM

处理难解E步的另一种方法是使用蒙特卡洛近似来估计充分统计量的期望值。具体来说，我们从后验分布中采样 $\boldsymbol{z}_n^s \sim p\left(\boldsymbol{z}_n \mid \boldsymbol{x}_n, \boldsymbol{\theta}^t\right)$，然后为每个完整数据向量 $\left(\boldsymbol{x}_n, \boldsymbol{z}_n^s\right)$ 计算充分统计量，最后对结果取平均。这种方法称为蒙特卡洛EM（MCEM）[WT90; Nea12]。

采样可以使用MCMC方法（参见第12章）。但如果每个E步都需要等待MCMC收敛，计算效率会很低。另一种方法是采用随机近似，在E步只进行”简短”采样后就执行部分参数更新，这称为随机近似EM（stochastic approximation EM）[DLM99]，其性能通常优于MCEM。

6.5.6.4 广义EM

当E步可以精确计算但M步难以精确求解时，我们仍可通过执行”部分”M步来保证对数似然的单调递增——此时只需提升（而非最大化）完全数据对数似然的期望。例如，可沿梯度方向执行若干步更新，该方法称为广义EM（generalized EM，GEM）算法[MK07]。（注：虽然”广义EM”这一术语未能涵盖EM算法的各类推广形式，但已成为标准术语。）以[Lan95a]为例，该方法建议采用单步Newton-Raphson更新：

\[\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t-\eta_t \mathbf{H}_t^{-1} \boldsymbol{g}_t \tag{6.171}\]

其中 $0<\eta_t \leq 1$ 表示步长，

\[\begin{align} \boldsymbol{g}_t & =\left.\frac{\partial}{\partial \boldsymbol{\theta}} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}_t\right)\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_t} \tag{6.172} \\ \mathbf{H}_t & =\left.\frac{\partial^2}{\partial \boldsymbol{\theta} \partial \boldsymbol{\theta}^{\top}} Q\left(\boldsymbol{\theta}, \boldsymbol{\theta}_t\right)\right|_{\boldsymbol{\theta}=\boldsymbol{\theta}_t} \tag{6.173} \end{align}\]

当步长 $\eta_t = 1$ 时，[Lan95a] 将其称为梯度EM算法。然而，如[Lan95b]的拟牛顿EM算法所示，可以采用更大的步长来加速收敛。该方法还使用BFGS近似替代方程(6.173)中的Hessian矩阵（对于非指数族模型，该矩阵可能非负定），从而确保整体算法保持上升特性。但需注意，当M步无法解析求解时，EM算法相对于直接使用基于梯度的求解器优化边缘似然的优势将有所减弱。

6.5.6.5 ECM 算法

ECM算法全称为“期望条件最大化”（expectation conditional maximization），指当参数存在依赖关系时在M步中依次优化这些参数。ECME算法全称为“ECM二者选一”（ECM either）[LR95]，是ECM的一种变体，其在一个或多个条件最大化步骤中，按常规方式最大化完整数据对数似然的期望（即Q函数），或直接最大化观测数据对数似然。后者可能显著加快计算速度，因为它忽略E步的结果而直接优化目标函数。一个典型例子是拟合学生t分布时：对于固定的 $\nu$，我们可以按常规方式更新 $\Sigma$，但在更新 $\nu$ 时，我们将标准更新形式 $\nu^{t+1}=\arg \max _\nu Q\left(\left(\boldsymbol{\mu}^{t+1}, \boldsymbol{\Sigma}^{t+1}, \nu\right), \boldsymbol{\theta}^t\right)$ 替换为 $\nu^{t+1}=\arg \max _\nu \log p\left(\mathcal{D} \mid \boldsymbol{\mu}^{t+1}, \mathbf{\Sigma}^{t+1}, \nu\right)$。更多细节参见[MK97]。

6.5.6.6 在线 EM

在处理大规模或流式数据集时，能够进行在线学习非常重要，正如我们在第19.7.5节讨论的那样。文献中主要有两种在线EM方法。第一种方法称为增量EM（incremental EM）[NH98a]，它逐个优化下界 $Q(\theta, q_1, \ldots, q_N)$ 中的$q_n$，但这种方法需要存储每个数据点的期望充分统计量。

第二种方法称为逐步EM（stepwise EM）[SI00; LK09; CM09]，它基于随机梯度下降（stochastic gradient descent），在每一步优化 \(\ln(\theta) = \log p(x_n|\theta)\) 的局部上界。（关于随机和增量边界优化算法的更一般讨论，可参见[Mai13; Mai15]。）

6.6 贝叶斯优化

在本节中，我们将讨论贝叶斯优化（Bayesian optimization，BayesOpt），这是一种基于模型的黑箱优化方法，专为目标函数 $ f : \mathcal{X} \to \mathbb{R} $ 评估成本高昂的场景设计（例如需要运行模拟实验，或训练测试特定神经网络架构的情形）。

由于真实函数 $ f $ 的评估代价昂贵，我们希望尽可能减少函数调用次数（即向预言机 $ f $ 发起查询 $ x $ 的次数）。这意味着需要基于当前收集的数据 $ D_n = {(x_i, y_i) : i = 1 : n} $ 构建一个代理函数（surrogate function）（亦称响应面模型（response surface model）），用以决策下一个查询点。这里存在一个固有权衡：选择我们认为 $ f(x) $ 会很大的查询点（遵循文献惯例，我们假设目标是最大化 $ f $），还是选择不确定性很高的区域的点——这些区域的点可能进一步提升代理函数。这实质上是探索-利用困境的又一典型场景。

探索：尝试未知区域，可能找到更优解。
利用：在已知表现好的区域进一步搜索。

在我们优化的定义域为有限集的特殊情况下，即 $\mathcal{X} = {1, \ldots, A}$ 时，贝叶斯优化问题就变得类似于赌博机文献中的最佳臂识别问题（第34.4节）。一个重要的区别在于：在赌博机问题中，我们关心每一步行动带来的代价，而在优化问题中，我们通常只关心最终找到的解的代价。换言之，在赌博机问题中，我们希望最小化累积遗憾，而在优化中，我们希望最小化简单遗憾或最终遗憾。

另一相关领域是主动学习，其目标是以最少查询次数完整地确定函数 $ f $，而贝叶斯优化仅需确定函数最大值。

贝叶斯优化是一个广阔的研究领域，下文仅作简要概述。更多细节可参阅 [Sha+16; Fra18; Gar23] 等文献（另可访问 https://distill.pub/2020/bayesian-optimization/ 查看交互式教程）。

6.6.1 基于序列模型的优化

贝叶斯优化是基于序列模型的优化策略的一个典型实例 [HHLB11]。该方法的核心思想在于交替执行两个步骤：在某个点处查询函数值，然后基于新获得的数据更新代理模型。具体而言，在每次迭代 $ n $ ，我们拥有一个带标签的数据集 \(D_n = { (x_i, y_i) : i = 1 : n }\)， 其中记录了已查询的点 $ x_i $ 及其对应的函数值 \(y_i = f(x_i) + \epsilon_i\) （$ \epsilon_i $ 为可选的噪声项）。利用该数据集，我们估计真实函数 $ f $ 的概率分布，记作 \(p(f|D_n)\) 。随后通过采集函数（acquisition function） $ \alpha(x; D_n) $ 选择下一个查询点 $ x_{n+1} $，该函数用于计算查询点 $ x $ 的期望效用（采集函数将在第6.6.3节详细讨论）。在观测到 \(y_{n+1} = f(x_{n+1}) + \epsilon_{n+1}\) 后，更新对函数的认知并重复上述过程。具体算法流程可参见算法6.5的伪代码实现。

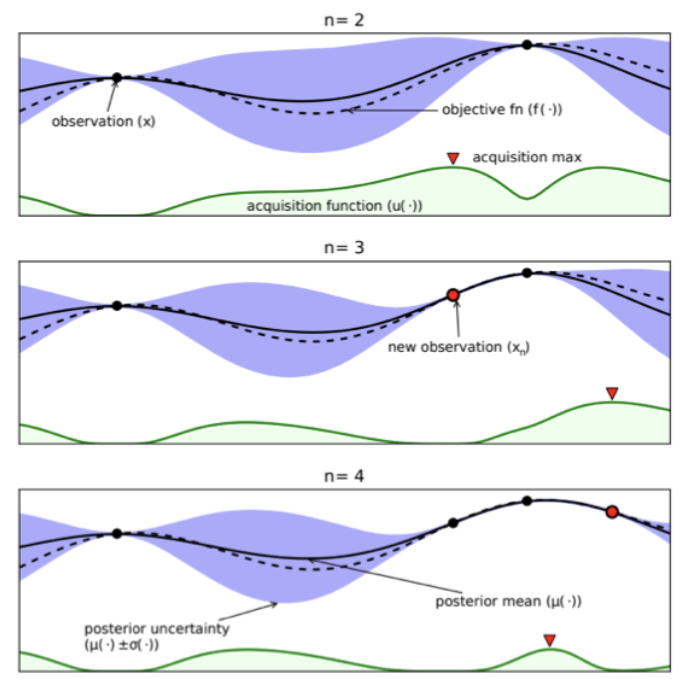
该方法的工作原理如图6.10所示，其目标是找到黑色实线所代表函数的全局最优点。首行展示了先前查询的两个点 $ x_1 $ 和 $ x_2 $ 及其对应函数值 $ y_1 = f(x_1) $ 与 $ y_2 = f(x_2) $。由于在这些位置对函数 $ f $ 取值的不确定性为零（假设观测无噪声），后验置信区间（蓝色阴影区域）呈现“收缩”特征。相应地，采集函数（底部绿色曲线）在这些已查询点处的取值也为零。红色三角形标示了采集函数的极大值点，即下一个待查询点 $ x_3 $。第二行图示呈现了观测 $ y_3 = f(x_3) $ 后的结果，此举进一步降低了对函数形态的不确定性。第三行则展示了观测 $ y_4 = f(x_4) $ 后的状态。该过程将持续迭代，直至时间耗尽或确信不存在更具潜力的未探索查询点。

构建贝叶斯优化算法需要提供两大核心要素：（1）表征并更新后验代理模型 \(p(f|D_n)\) 的方法；（2）定义并优化采集函数 \(\alpha(\boldsymbol{x}; D_n)\) 的方法。下文将分别对这两个主题展开讨论。

6.6.2 代理函数

在本节中，我们将讨论函数后验分布 \(p(f|D)\) 的表示与更新方法。

6.6.2.1 高斯过程

在贝叶斯优化中，采用高斯过程作为代理模型是极为常见的做法。高斯过程的详细原理将在第18章阐述，其核心思想是将 \(p(f(x)|\mathcal{D}_n)\) 表示为高斯分布 \(\mathcal{N}(f|\mu_n(x), \sigma_n^2(x))\)， 其中均值函数 $\mu_n(x)$ 与方差函数 $\sigma_n(x)$ 可通过训练数据 \(\mathcal{D}_n = {(x_i, y_i) : i = 1 : n}\) 经由闭式解析方程推导得出。高斯过程需要预设核函数 $K_\theta(x, x’)$ 来衡量输入点 $x, x’$ 之间的相似度。其直观原理在于：若两个输入点相似度较高（即 $K_\theta(x, x’)$ 取值较大），则对应函数值也倾向于相似，故 $f(x)$ 与 $f(x’)$ 应呈正相关。这一特性使我们可以基于标注训练点对函数进行插值估计，在某些情况下还能实现函数的外推预测。

高斯过程在训练数据稀缺时表现优异，且支持闭式贝叶斯更新。然而，精确更新的时间复杂度为 $O(N^3)$（$N$ 为样本量），当函数评估次数较多时计算效率会显著下降。现有多种方法（第18.5.3节）可将复杂度降至 $O(NM^2)$（$M$ 为可调参数），但会牺牲部分计算精度。

此外，高斯过程的性能高度依赖于优质核函数的选择。如第18.6.1节所述，可通过最大化边缘似然来估计核参数 $\theta$。但由于样本量通常较小（这是该方法的前提假设），采用第18.6.2节介绍的近似贝叶斯推断方法对 $\theta$ 进行边缘化处理往往能获得更优的性能表现。更多技术细节可参阅 [WF16] 等文献。

6.6.2.2 贝叶斯神经网络

高斯过程的一个自然替代方案是使用参数化模型。若采用线性回归，我们可以如第15.2节所示高效执行精确贝叶斯推断。若使用非线性模型（如深度神经网络），则需借助近似推断方法。我们将在第17章详细讨论贝叶斯神经网络，其于贝叶斯优化的应用可参阅[Spr+16; PPR22; Kim+22]等文献。

6.6.2.3 其他方法

我们完全可以采用其他形式的回归模型。[HHLB11] 使用了随机森林集成方法；如第6.6.4.2节所述，此类模型能轻松处理条件参数空间，但通过自助法获取不确定性估计的过程可能较为耗时。

6.6.3 采集函数

在贝叶斯优化中，我们通过采集函数（亦称评价函数）来评估每个潜在查询点的期望效用： \(\alpha\left(\boldsymbol{x} \mid \mathcal{D}_n\right)=\mathbb{E}_{p\left(y \mid \boldsymbol{x}, \mathcal{D}_n\right)}\left[U\left(\boldsymbol{x}, y ; \mathcal{D}_n\right)\right]\)， 其中 \(y = f(\boldsymbol{x})\) 表示点 $\boldsymbol{x}$ 处未知的函数值，$ U() $ 为效用函数。正如后续将讨论的，不同的效用函数会衍生出不同的采集函数。我们通常选择的函数会使得已查询点的效用值较小（在无噪声观测场景下甚至为零），以此促进探索行为。

6.6.3.1 改进的概率

定义 $ M_n = \max_{i=1}^n y_i $ 为当前已观测的最优值（称为当前最优值）。（若观测存在噪声，采用最高均值 $ \max_i E_{p(f|D_n)} [f(x_i)] $ 是合理的替代方案 [WF16]。）随后我们通过 $ U(x, y; D_n) = I(y > M_n) $ 定义新点 $ x $ 的效用，该函数仅当新值优于当前最优值时产生奖励。相应的采集函数即为期望效用 $ \alpha_{PI}(x; D_n) = p(f(x) > M_n | D_n) $， 这被称为提升概率[Kus64]。若 $ p(f|D_n) $ 是高斯过程，则该量值可通过以下闭式解计算：

\[\alpha_{P I}\left(\boldsymbol{x} ; \mathcal{D}_n\right)=p\left(f(\boldsymbol{x})>M_n \mid \mathcal{D}_n\right)=\Phi\left(\gamma_n\left(\boldsymbol{x}, M_n\right)\right) \tag{6.174}\]

其中 $\Phi$ 表示标准正态分布 $\mathcal{N}(0,1)$ 的累积分布函数，且

\[\gamma_n(\boldsymbol{x}, \tau)=\frac{\mu_n(\boldsymbol{x})-\tau}{\sigma_n(\boldsymbol{x})} \tag{6.175}\]

6.6.3.2 期望提升

PI方法的问题在于所有提升都被视为同等重要，因此该方法倾向于采取较强的利用倾向[Jon01]。一种常见的改进方案通过定义 $ U(x,y;D_n) = (y - M_n)I(y > M_n) $ 来考虑提升幅度，并得到：

\[\alpha_{EI}(x;D_n) = \mathbb{E}_{D_n}[U(x,y)] = \mathbb{E}_{D_n}[(f(x) - M_n)I(f(x) > M_n)] \tag{6.176}\]

该采集函数被称为期望提升准则[Moc+96]。当采用高斯过程代理模型时，其闭式解为：

\[\alpha_{EI}(x;D_n) = (\mu_n(x) - M_n)\Phi(\gamma) + \sigma_n(x)\phi(\gamma) = \sigma_n(x)[\gamma_n\Phi(\gamma) + \phi(\gamma)] \tag{6.177}\]

其中 $\phi()$ 为标准正态分布 $\mathcal{N}(0,1)$ 的概率密度函数，$\Phi$ 为其累积分布函数，$\gamma = \gamma_n(x, M_n)$。第一项促进利用（评估高均值点），第二项促进探索（评估高方差点）。该特性如图6.10所示。

若无法解析计算预测方差但能获取后验采样，则可按[Kim+22]提出的方法通过蒙特卡洛近似计算EI：

\[\alpha_{EI}(x; D_n) \approx \frac{1}{S} \sum_{s=1}^{S} \max(\mu_n^s(x) - M_n, 0) \tag{6.178}\]

6.6.3.3 上置信界

另一种方法是计算函数在置信水平 $\beta_n$ 下的上置信界，并定义采集函数为：$\alpha_{U C B}\left(\boldsymbol{x} ; \mathcal{D}_n\right)=\mu_n(\boldsymbol{x})+\beta_n \sigma_n(\boldsymbol{x})$。这与情境赌博机设置（第34.4.5节）原理相同，区别在于此处是对 $x \in \mathcal{X}$ 进行优化，而非有限臂集 $a \in {1, \ldots, A}$。若使用高斯过程作为代理模型，该方法称为GP-UCB[Sri+10]。

6.6.3.4 汤普森采样

我们在第34.4.6节讨论过多臂赌博机中的汤普森采样，其中状态空间有限 $\mathcal{X} = {1, \ldots, A}$，采集函数 $\alpha(a; D_n)$ 对应臂 $a$ 为最佳臂的概率。通过下式可将其推广至实值输入空间 $\mathcal{X}$：

\[\alpha\left(\boldsymbol{x} ; \mathcal{D}_n\right)=\mathbb{E}_{p\left(\boldsymbol{\theta} \mid \mathcal{D}_n\right)}\left[\mathbb{I}\left(\boldsymbol{x}=\underset{\boldsymbol{x}^{\prime}}{\operatorname{argmax}} f_{\boldsymbol{\theta}}\left(\boldsymbol{x}^{\prime}\right)\right)\right] \tag{6.179}\]

通过对 $\tilde{\theta} \sim p(\theta|D_n)$ 进行采样，可得到该积分的单样本近似。随后通过下式选择最优动作：

\[\boldsymbol{x}_{n+1}=\underset{\boldsymbol{x}}{\operatorname{argmax}} \alpha\left(\boldsymbol{x} ; \mathcal{D}_n\right)=\underset{\boldsymbol{x}}{\operatorname{argmax}} \mathbb{I}\left(\boldsymbol{x}=\underset{\boldsymbol{x}^{\prime}}{\operatorname{argmax}} f_{\hat{\theta}}\left(\boldsymbol{x}^{\prime}\right)\right)=\underset{\boldsymbol{x}}{\operatorname{argmax}} f_{\hat{\theta}}(\boldsymbol{x}) \tag{6.180}\]

换言之，我们对采样得到的代理函数进行贪婪最大化。

对于连续空间，汤普森采样比赌博机场景更难应用，因为我们无法直接从采样函数中计算最佳“臂” $\boldsymbol{x}_{n+1}$。此外，使用高斯过程时，与参数化代理模型的参数采样相比，函数采样存在微妙的技术难点（参见[HLHG14]的讨论）。

6.6.3.5 熵搜索

由于贝叶斯优化的目标是找到 \(x^* = \text{argmax}_x f(x)\)， 直接最小化对 \(x^*\) 位置的不确定性（记为 \(p_*(x|D_n)\) ）是合理的。因此我们定义效用函数为：

\[U\left(\boldsymbol{x}, y ; \mathcal{D}_n\right)=\mathbb{H}\left(\boldsymbol{x}^* \mid \mathcal{D}_n\right)-\mathbb{H}\left(\boldsymbol{x}^* \mid \mathcal{D}_n \cup\{(\boldsymbol{x}, y)\}\right) \tag{6.181}\]

其中 \(\mathbb{H}(x^*|D_n) = \mathbb{H}(p_*(x|D_n))\) 是最优点位置后验分布的熵。这被称为信息增益准则；与主动学习目标的区别在于，此处我们希望获取关于 $ x^* $ 的信息而非所有 $ x $ 对应的 $ f $ 信息。相应采集函数为：

\[\alpha_{E S}\left(\boldsymbol{x} ; \mathcal{D}_n\right)=\mathbb{E}_{p\left(y \mid \boldsymbol{x}, \mathcal{D}_n\right)}\left[U\left(\boldsymbol{x}, y ; \mathcal{D}_n\right)\right]=\mathbb{H}\left(\boldsymbol{x}^* \mid \mathcal{D}_n\right)-\mathbb{E}_{p\left\{y \mid \boldsymbol{x}, \mathcal{D}_n\right)}\left[\mathbb{H}\left(\boldsymbol{x}^* \mid \mathcal{D}_n \cup\{(\boldsymbol{x}, y)\}\right)\right] \tag{6.182}\]

该方法称为熵搜索[HS12]。

遗憾的是，计算 $ \mathbb{H}(x^*|D_n) $ 非常困难，因其需要输入空间上的概率模型。幸运的是，我们可以利用互信息的对称性将式(6.182)的采集函数重写为：

\[\alpha_{P E S}\left(\boldsymbol{x} ; \mathcal{D}_n\right)=\mathbb{H}\left(y \mid \mathcal{D}_n, \boldsymbol{x}\right)-\mathbb{E}_{\boldsymbol{x}^* \mid \mathcal{D}_n}\left[\mathbb{H}\left(y \mid \mathcal{D}_n, \boldsymbol{x}, \boldsymbol{x}^*\right)\right] \tag{6.183}\]

其中可通过汤普森采样近似 $ p(x^*|D_n) $ 的期望。现在只需对输出空间 $ y $ 的不确定性进行建模。该方法称为预测熵搜索[HLHG14]。

6.6.3.6 知识梯度

目前讨论的采集函数均属于贪婪策略，因其仅考虑单步前瞻。知识梯度采集函数[FPD09]通过考虑查询 $\boldsymbol{x}$ 后更新后验分布，并基于新认知进行最大化利用所能获得的期望改进，实现了两步前瞻。具体而言，定义查询一个新点后能找到的最佳值：

\[\begin{align} V_{n+1}(\boldsymbol{x}, y) & =\max _{\boldsymbol{x}^{\prime}} \mathbb{E}_{p\left(f \mid \boldsymbol{x}, y, \mathcal{D}_n\right)}\left[f\left(\boldsymbol{x}^{\prime}\right)\right] \tag{6.184}\\ V_{n+1}(\boldsymbol{x}) & =\mathbb{E}_{p\left(y \mid \boldsymbol{x}, \mathcal{D}_n\right)}\left[V_{n+1}(\boldsymbol{x}, y)\right] \tag{6.185} \end{align}\]

定义KG采集函数为：

\[\alpha_{K G}\left(\boldsymbol{x} ; \mathcal{D}_n\right)=\mathbb{E}_{\mathcal{D}_n}\left[\left(V_{n+1}(\boldsymbol{x})-M_n\right) \mathbb{I}\left(V_{n+1}(\boldsymbol{x})>M_n\right)\right] \tag{6.186}\]

将此式与式(6.176)的EI函数对比可知，我们选择的点 \(\boldsymbol{x}_{n+1}\) 应使得观测 \(f(\boldsymbol{x}_{n+1})\) 能提供可供利用的知识，而非直接寻找具有更优 $f$ 值的点。

6.6.3.7 采集函数优化

采集函数 $\alpha(\boldsymbol{x})$ 通常是多峰函数（例如图6.11所示），因为在所有已查询点处（假设无噪声观测）其值均为0。因此最大化该函数本身可能构成一个复杂的子问题[WHD18; Rub+20]。

在连续设置中，常采用多起点BFGS或网格搜索。也可使用交叉熵方法（第6.7.5节），采用高斯混合模型[BK10]或VAE[Fau+18]作为 $\boldsymbol{x}$ 的生成模型。在离散组合设置中（如优化生物序列），[Bel+19]采用正则化进化（第6.7.3节），[Ang+20]采用近端策略优化（第35.3.4节）。还有许多其他组合方法可供选择。

6.6.4 其他问题

应用贝叶斯优化时还需解决诸多问题，以下简要讨论其中几个。

6.6.4.1 并行（批量）查询

某些场景下需要对目标函数进行并行多点查询，这被称为批量贝叶斯优化。此时需要优化可能的查询集合，其计算复杂度比常规情况更高。该领域的最新研究可参阅[WHD18; DBB20]。

6.6.4.2 条件参数

贝叶斯优化常应用于超参数优化。在许多场景中，某些超参数仅当其他参数取特定值时才有效。例如在Auto-Sklearn系统[Feu+15]或Auto-WEKA系统[Kot+17]的自动分类器调优中：若选择神经网络方法，需指定层数和每层隐藏单元数；但若选择决策树，则需指定最大树深度等不同超参数。

可通过树结构或有向无环图定义搜索空间来形式化此类问题，其中每个叶节点定义不同的参数子集。在该设置中应用高斯过程需要非标准核函数，如[Swe+13; Jen+17]所讨论的方法。另一种方案是使用随机森林集成[HHLB11]等贝叶斯回归方法，这类方法能轻松处理条件参数空间。

6.6.4.3 多保真度代理模型

某些情况下可构建具有不同精度等级的代理函数，各等级的计算耗时可能不同。具体而言，令 $ f(x,s) $ 为在保真度 $ s $ 下对真实函数的近似。目标是通过在序列 $(x_i,s_i)$ 处观测 $ f(x,s) $ 来求解 $\max_{x} f(x,0)$，且需满足总成本 $\sum_{i=1}^n c(s_i)$ 不超过预算。例如在超参数选择中，$ s $ 可控制参数优化器的运行时长或验证集规模。

除选择实验保真度外，若廉价代理指标显示某昂贵试验不值得完整执行，可提前终止该查询（参见[Str19; Li+17c; FKH17]）。另一种方案是恢复早期中止的运行以收集更多数据，如冻结-解冻算法[SSA14]所示。

6.6.4.4 约束优化

若需要在已知约束下最大化函数，可直接将约束纳入采集函数。但若约束未知，则除估计函数外还需估计可行集的支撑域。[GSA14]提出加权EI准则 \(\alpha_{wEI}(\boldsymbol{x}; \mathcal{D}_n) = \alpha_{EI}(\boldsymbol{x}; \mathcal{D}_n)h(\boldsymbol{x}; \mathcal{D}_n)\)， 其中 \(h(\boldsymbol{x}; \mathcal{D}_n)\) 是采用伯努利观测模型的高斯过程，用于判断 \(\boldsymbol{x}\) 是否可行。当然也存在其他方法，例如[HL+16b]提出了基于预测熵搜索的解决方案。

6.7 Derivative-free 优化

无导数优化（Derivative-free optimization, DFO） 是指在优化过程中不需要使用导数的方法，适用于黑盒函数优化和离散优化问题。若函数的计算成本较高，可采用贝叶斯优化（见第6.6节）；若函数计算成本较低，则可使用随机局部搜索或进化搜索方法，下文将详细讨论。

6.7.1 局部搜索

本节将讨论针对离散的非结构化搜索空间的启发式全局优化算法。这类算法不再使用局部梯度实现参数更新（即 $\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_t+\eta_t \boldsymbol{d}_t$），而是采用离散形式的更新机制：

\[\boldsymbol{x}_{t+1}=\underset{\boldsymbol{x} \in \operatorname{nbr}\left(\boldsymbol{x}_t\right)}{\operatorname{argmax}} \mathcal{L}(\boldsymbol{x}) \tag{6.187}\]

其中，$\operatorname{nbr}\left(\boldsymbol{x}_t\right) \subseteq \mathcal{X}$ 表示当前解 $\boldsymbol{x}_t$ 的邻域集合。该方法被称为爬山法（hill climbing）、最速上升法（steepest ascent） 或贪心搜索（greedy search）。

如果某个点的“邻域”包含整个解空间，则式（6.187）将直接返回全局最优解。但全局邻域往往因为过大而导致无法穷举。因此，我们通常需要定义一个局部邻域。以八皇后问题为例：该问题要求在 $8\times8$ 的棋盘上放置皇后并使其互不攻击（见图6.14）。该问题所对应的状态空间大小为 $\mathcal{X}=64^8$，但由于约束条件，实际只有约1700万（$8^8$）个可行状态。我们将一个状态的邻域定义为：通过移动单个皇后到同列其他方格生成的所有可能状态，因此每个状态节点有$8\times7=56$个邻居节点。根据[RN10, p.123]，若从随机生成的八皇后状态开始，最速上升法有$86\%$的概率陷入局部最优，仅有$14\%$的概率获得全局最优解，但该算法的速度很快——成功时平均需要 $4$ 步，失败时平均仅需要 $3$ 步。

6.7.1.1 随机局部搜索

爬山法是一种贪心算法，因为它需要精确求解方程（6.187），所以总是选择当前邻域内的最优点。为了降低陷入局部最优的风险，可以采用近似最大化目标函数的方法：例如定义一个关于优化方向的概率分布（优化增益越大的方向对应的概率越高），然后随机选择参数更新的方向，这种方法称为随机爬山法（stochastic hill climbing）。若逐步降低该概率分布的熵（即随时间推移逐渐增强贪心特性），就形成了模拟退火算法，我们将在12.9.1节详细讨论这一方法。

另一种简单的方法是使用贪心版本的爬山算法，但每当达到局部最优时，就从另一个随机起点重新开始。这种方法称为随机重启爬山算法（random restart hill climbing）。为了理解其优势，我们再次以八皇后问题为例：如果每次爬山搜索的成功概率为 $p \approx 0.14$，那么平均需要 $R=1 / p \approx 7$ 次重启才能找到有效解。总步数的期望值可如下计算：设成功所需要的平均步数 $N_1=4$，失败所需要的平均步数 $N_0=3$，则总平均步数为 $N_1+(R-1) N_0=4+6 \times 3=22$。由于单步计算速度极快，该算法整体效率非常高——例如能在1分钟内求解 $n=1 \mathrm{M}$ 的n皇后问题。

当然，解决n皇后问题在实际应用中并非最具实用价值的任务。但它却是众多布尔可满足性问题（Boolean satisfiability problems）的典型代表——这类问题广泛存在于从人工智能规划到模型检测的各个领域（参见文献[SLM92]）。令人惊讶的是，我们所讨论的这类简单随机局部搜索算法（Stochastic Local Search, SLS）在此类问题上表现极为出色（参见文献[HS05]）。

6.7.1.2 Tabu search

爬山算法一旦到达局部最优解或平台期就会停止更新。显然可以执行随机重启，但这样做会丢失此前获得的所有信息。一种更智能的替代方案称为禁忌搜索（Tabu search）[GL97]。该方法与爬山算法类似，但允许移动到降低（或至少不提高）目标函数的新状态——只要该状态此前未被访问过。我们可以通过维护一个记录最近 $\tau$ 个已访问状态的禁忌列表来实现这一点。这种机制强制算法探索新的状态，从而增加逃离局部最大值的概率。该过程持续进行直至达到 $c_{\max }$ 步（称为”禁忌期限”）。伪代码参考算法6.6。（若设置 $c_{\max }=1$，则退化为贪婪爬山算法。）

例如，考虑当禁忌搜索到达山顶 \(\boldsymbol{x}_t\) 时的情况。在下一步中，算法将移动到峰顶的某个相邻点 \(\boldsymbol{x}_{t+1} \in \operatorname{nbr}\left(\boldsymbol{x}_t\right)\) ——该点函数值必然更低。接着它会移动到上一步的相邻点 \(\boldsymbol{x}_{t+2} \in \operatorname{nbr}\left(\boldsymbol{x}_{t+1}\right)\)； 此时禁忌列表会阻止其返回 $\boldsymbol{x}_t$（峰顶），因此算法被迫选择同等高度或更低的相邻点。如此持续”环绕”峰顶运行，可能被迫下坡至更低水平的解的集合（类似逆向盆地淹没操作），直到发现通往新峰顶的山脊，或超过禁忌期限。

根据[RN10, p.123]所述，禁忌搜索将八皇后问题的解决率从 $14\%$ 提升至 $94\%$，不过该种算法每次成功平均需要 $21$ 步，每次失败则平均需要 $64$ 步。

6.7.1.3 Random search

在某些情况下，我们对目标函数一无所知（比如是否可导，凹凸性如何，计算复杂度等），此时，使用随机搜索（random search）的方法往往能取得不错的效果。在该方法中，每一次迭代 $\boldsymbol{x}_{t+1}$ 是从优化空间 $\mathcal{X}$ 均匀采样的结果。在实际过程中，这类方法应该作为baseline进行尝试。

[BB12] 将这种技术（随机搜索）应用于一些机器学习模型的超参数优化问题，其优化目标是模型在验证集上的性能。在他们的例子中，搜索空间是连续的，即 $\Theta=[0,1]^D$。从这个空间中随机采样非常容易。相应的替代方法是将空间量化为一个固定的值集，然后全部评估一遍；这种方法被称为网格搜索（grid search）。（当然，这只有在维度 $D$ 较小的情况下才可行。）他们发现，随机搜索的性能优于网格搜索。其直观原因是，许多超参数对目标函数（模型性能）影响甚微，如图 6.12 所示。因此，沿着这些不重要的维度设置精细的网格是在浪费时间。

随机搜索（RS）也被用于优化马尔可夫决策过程（MDP）策略的参数，其目标函数的形式为 \(f(\boldsymbol{x})=\mathbb{E}_{\boldsymbol{\tau} \sim \pi_{\boldsymbol{x}}}[R(\boldsymbol{\tau})]\)， 即使用参数为 $\boldsymbol{x}$ 的策略所生成的轨迹的期望奖励。对于自由参数较少的策略，随机搜索的性能可以超越第35章中描述的更复杂的强化学习方法，正如 [MGR18] 中所展示的。在策略参数数量巨大的情况下，有时可以将其投影到一个更低维的随机子空间中，并在该子空间内进行优化（可以是网格搜索或随机搜索）[Li+18a]。

6.7.2 模拟退火

模拟退火（Simulated annealing） [KJV83; LA87] 是一种随机局部搜索算法（stochastic local search）（第6.7.1.1节），旨在找到某个黑箱函数 $\mathcal{E}(\boldsymbol{x})$ 的全局最小值，其中 $\mathcal{E}(\boldsymbol{x})$ 被称为能量函数（energy function）。该方法的原理是，通过定义 $p(\boldsymbol{x})=\exp (-\mathcal{E}(\boldsymbol{x}))$ 将能量转换为关于状态的（未归一化的）概率分布，然后使用Metropolis-Hastings算法的变体从一系列概率分布中进行采样。这一系列分布经过精心设计，使得在算法的最后一步，该方法能够从该分布的其中一个模式（mode） 中采样，即找到最可能的状态之一，或能量最低的状态之一。这种方法可同时用于离散和连续优化。更多细节请参见第12.9.1节。

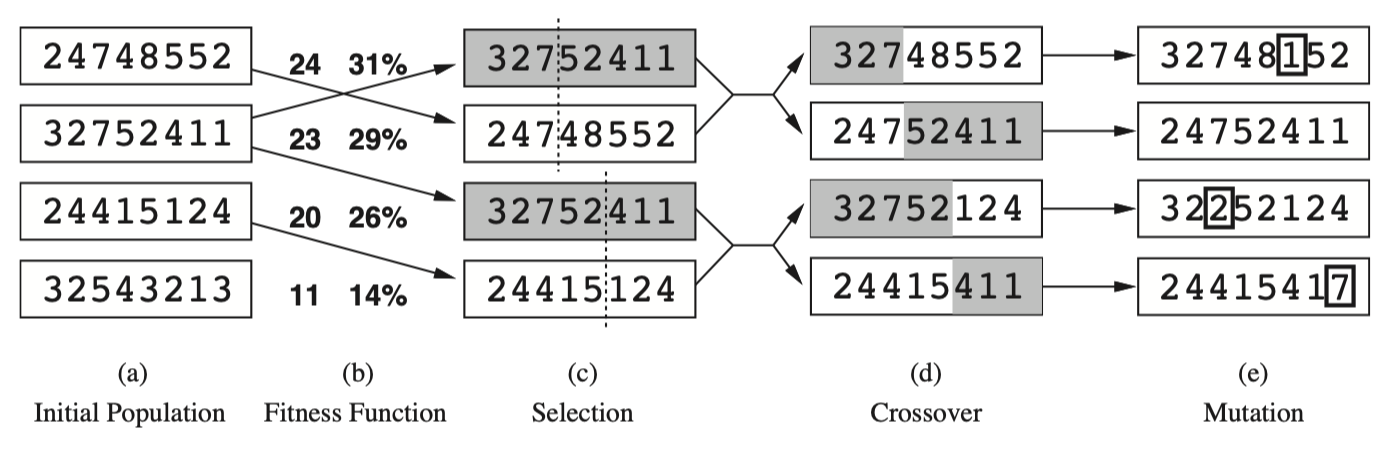
6.7.3 进化算法

随机局部搜索（SLS）在每一步都维护一个单一的“最佳猜测”解 $\boldsymbol{x}_t$。如果我们运行 $T$ 步，并重启 $K$ 次，总成本是 $TK$。一个很自然的替代方法是维护一个由 $K$ 个优质候选解组成的集合或种群（Population） $\mathcal{S}_t$，我们尝试在每一步改进这个种群。这被称为进化算法（evolutionary algorithm，EA）。如果我们运行 $T$ 步，它同样需要 $TK$ 的时间成本；然而，它通常能比多次重启的SLS获得更好的结果，因为其搜索过程并行地探索了更多的空间，并且种群中不同成员之间的信息可以共享。正如我们下文将要讨论的，进化算法有许多可能的变体。

由于进化算法（EA）是从生物进化过程中汲取灵感，因此它也借用了大量的生物学术语。种群中某个成员的适应度（Fitness） 即目标函数值（可能还会在种群成员间进行归一化）。在第 $t+1$ 步时的种群成员被称为后代（Offspring）。这些后代可以通过从 $\mathcal{S}_t$ 中随机选择一个父代（Parent） 并对其施加一个随机变异（Mutation） 来创建——类似于无性繁殖。或者，我们也可以通过从 $\mathcal{S}_t$ 中选择两个父代，并以某种方式将它们组合来产生一个子代（Child）——类似于有性繁殖；这种组合父代的过程被称为重组（Recombination），（该过程之后通常还会伴随着变异）。

选择父代的过程被称为选择函数（Selection Function）。在截断选择（Truncation Selection） 中，每个父代都是从种群中适应度最高的 $K$ 个成员（称为精英集，Elite Set）中选出的。在锦标赛选择（Tournament Selection） 中，每个父代是随机选择的 $K$ 个成员中适应度最高的那一个。在适应度比例选择（Fitness Proportionate Selection），也称为轮盘赌选择（Roulette Wheel Selection） 中，每个父代被选中的概率与其相对于其他成员的适应度成正比。我们还可以“淘汰”种群中最老的成员，然后根据适应度来选择父代；这被称为正则化进化（Regularized Evolution）[Rea+19]。

除了父代的选择规则外，我们还需要规定重组和变异的规则。这些启发式算法有许多可能的选择。下面我们简要介绍其中的几种。

• 在遗传算法（genetic algorithm, GA） [Gol89; Hol92] 中，我们使用变异和一种基于交叉（crossover） 的特定重组方法。为了实现交叉操作，我们类比染色体，假设每个个体都表示为一个整数或二进制数组成的向量。我们为选定的两个父代个体分别沿着染色体选取一个分割点，然后交换分割点后的字符串（基因片段），如图 6.13 所示。
• 在遗传编程（genetic programming, GP） [Koz92] 中，我们使用树形结构来表示个体，而不是位串。这种表示法确保了所有的交叉操作都能产生有效的子代，如图 6.15 所示。遗传编程在寻找优秀程序以及其他结构化对象（例如神经网络）时非常有用。在进化编程（EP） 中，树的结构是固定的，只有数值参数会被进化。
• 在代理辅助进化算法（Surrogate assisted EA） 中，使用一个代理函数 f(s) 来代替真实的目标函数 f(s)，以加速对种群成员的评估（综述请参见 [Jin11]）。这与贝叶斯优化（第6.6节）中使用的响应面模型类似，不同之处在于它不处理探索-利用权衡（explore-exploit tradeoff）。
• 在模因算法（Memetic Algorithm） [MC03] 中，我们将变异和重组与标准的局部搜索相结合。

进化算法已被应用于大量应用中，包括训练神经网络（这种组合被称为神经进化[Sta+19]）。一个高效的、基于 JAX 的（神经）进化库可以在 https://github.com/google/evojax 找到。

6.7.4 Estimation of distribution (EDA) 算法

进化算法（EA）维护着一个由优质候选解组成的种群，这可以被视为对高适应度状态的一种隐式的（非参数的）密度模型。[BC95] 的研究提出了一种“从遗传算法（GAs）中去除遗传操作”的方法，其核心是显式地在配置空间上学习一个概率模型，该模型将其概率质量集中于高分解上。也就是说，种群变成了一个生成模型的参数集 $\boldsymbol{\theta}_t$。

学习此类模型的一种方法如下。我们首先从当前模型中抽取 $K^{\prime}>K$ 个候选解，生成一个样本集 \(\mathcal{S}_t=\left\{\boldsymbol{x}_k \sim p\left(\boldsymbol{x} \mid \boldsymbol{\theta}_t\right)\right\}\)。 然后，我们使用适应度函数对这些样本进行排序，并利用一个选择算子（这被称为截断选择）挑选出最具前景的、大小为 $K$ 的子集 \(\mathcal{S}_t^*\)。 最后，我们使用最大似然估计，将一个新的概率模型 \(p\left(\boldsymbol{x} \mid \boldsymbol{\theta}_{t+1}\right)\) 拟合到 \(\mathcal{S}_t^*\) 上。这种方法被称为估计分布算法（EDA）（参见例如 [LL02; PSCP06; Hau+11; PHL12; Hu+12; San17; Bal17]）。

请注意，EDA 等价于最小化由 \(\mathcal{S}_t^*\) 定义的经验分布与模型分布 \(p\left(\boldsymbol{x} \mid \boldsymbol{\theta}_{t+1}\right)\) 之间的交叉熵。因此，EDA 与交叉熵方法（cross entropy method, CEM） 相关，正如第6.7.5节所述，尽管 CEM 通常假设 \(p(\boldsymbol{x} \mid \boldsymbol{\theta})=\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \mathbf{\Sigma})\) （即高斯分布）这一特例。EDA 也与 EM算法 密切相关，正如 [Bro+20a] 中所讨论的。

举一个简单的例子，假设配置空间是长度为 $D$ 的比特串，且适应度函数为 $f(x)=\sum_{d=1}^D x_d$（其中 $x_d \in{0,1}$，这在 EA 文献中被称为 one-max 函数）。针对此问题，一个简单的概率模型是形式为 $p(\boldsymbol{x} \mid \boldsymbol{\theta})=\prod_{d=1}^D \operatorname{Ber}\left(x_d \mid \theta_d\right)$ 的完全因子化模型。在分布式贝叶斯优化（DBO） 中使用此模型会得到一种称为单变量边际分布算法（UMDA） 的方法。

我们可以通过将参数 $\theta_d$ 设置为精英集 $\mathcal{S}_t^*$ 中第 $d$ 位为 1 的样本所占的比例来估计伯努利模型的参数。或者，我们也可以采用增量调整的方式来更新参数。基于种群增量学习的（PBIL）算法 [BC95] 将这一思想应用于因子化伯努利模型，得到了以下更新公式：

\[\hat{\theta}_{d, t+1}=\left(1-\eta_t\right) \hat{\theta}_{d, t}+\eta_t \bar{\theta}_{d, t} \tag{6.188}\]

其中 \(\bar{\theta}_{d, t}=\frac{1}{N_t} \sum_{k=1}^K \mathbb{I}\left(x_{k, d}=1\right)\) 是从当前迭代生成的 $K=\left|\mathcal{S}_t^*\right|$ 个样本中估计出的最大似然估计（MLE），而 $\eta_t$ 是一个学习率。

我们可以很直接地使用更具表达能力的概率模型来捕捉参数之间的依赖关系（这些依赖关系在 EA 文献中被称为构建块）。例如，在实值参数的情况下，我们可以使用一个多元高斯分布 $p(\boldsymbol{x})=\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \mathbf{\Sigma})$。由此产生的方法被称为多元正态分布估计算法（EMNA）[LL02]。（亦可参见第 6.7.5 节。）

对于离散随机变量，很自然地可以使用概率图模型（第4章）来捕捉变量之间的依赖关系。[BD97] 使用 Chow-Liu 算法（补充章节 30.2.1）学习了一个树结构的图模型；[BJV97] 是该方法的一个特例，其图模型限定为树结构。我们也可以学习更一般的图模型结构（例如参见 [LL02]）。我们通常使用贝叶斯网络（第4.2节），因为我们可以利用祖先采样（第4.2.5节）来轻松生成样本；因此，由此产生的方法被称为贝叶斯优化算法（BOA）[PGCP00]。分层贝叶斯优化算法（hBOA）[Pel05] 对此进行了扩展，它使用决策树和决策图（如 [CHM97] 中所述）来表示贝叶斯网络中的局部条件概率表（CPTs），而不是使用普通的表格。通常，为用于 EDA 而学习概率模型结构的过程被称为连锁学习，这是类比于如果基因可以作为构建块被共同遗传，那么它们就是连锁在一起的。

我们也可以使用深度生成模型来表示优质候选解的分布。例如，[CSF16] 使用了去噪自编码器和 NADE 模型（第22.2节），[Bal17] 使用了一个 DNN 回归器，然后通过对其输入进行梯度下降来求逆，[PRG17] 使用了 RBM（第4.3.3.2节），[GSM18] 使用了 VAE（第21.2节），等等。这类模型可能需要更多的数据来拟合（因此需要更多的函数调用），但有可能更真实地模拟概率分布景观。（然而，这是否会转化为更好的优化性能尚不清楚。）

6.7.5 交叉熵方法

6.7.6 进化策略

进入策略（Evolutionary strategies）[^Wie+14] 是一种基于分布的优化算法，其中的分布表示为高斯分布 \(p\left(\boldsymbol{x} \mid \boldsymbol{\theta}_t\right)\) （参考 [Sal+17b]）。与 CEM 不同，参数更新的方式是使用梯度下降，而不是关于精英集合中样本的MLE。更精确地讲，考虑光滑的目标函数 \(\mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{p(\boldsymbol{x} \mid \boldsymbol{\theta})}[f(\boldsymbol{x})]\)。 我们可以使用 REINFORCE 估计器（6.3.4节）来计算该目标函数的梯度：

\[\nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta})=\mathbb{E}_{p(\boldsymbol{x} \mid \boldsymbol{\theta})}\left[f(\boldsymbol{x}) \nabla_{\boldsymbol{\theta}} \log p(\boldsymbol{x} \mid \boldsymbol{\theta})\right] \tag{6.190}\]

上式可以通过采样蒙特卡洛样本进行近似。接下来我们将讨论如何计算该梯度。

6.7.6.1 自然进化策略

若概率模型属于指数族，我们可以计算自然梯度（第6.4节）而非“普通”梯度，从而加速收敛。此类方法称为自然进化策略[Wie+14]。

6.7.6.2 协方差矩阵自适应进化策略（CMA-ES）

[Han16]提出的CMA-ES（协方差矩阵自适应进化策略）是一种自然进化策略。除参数更新方式特殊外，其与交叉熵方法（CEM）高度相似。具体而言，该方法并非直接对精英集进行未加权最大似然估计来更新均值和协方差，而是根据精英样本的排名为其分配权重，随后将新的均值设为精英集的加权最大似然估计值。

协方差的更新公式更为复杂：通过“进化路径”累积连续代际的搜索方向，并据此更新协方差。研究证明[Oll+17]，这种更新方式可在不显式建模费雪信息矩阵的情况下，实现对 $\mathcal{L}(\boldsymbol{\theta})$ 自然梯度的近似。

图6.17展示了该方法的运行过程。

6.8 最优传输

本节重点介绍最优传输（optimal transport）理论。该理论由[Mon81]开创，是一套用于比较两个概率分布的工具集合。我们将从简单的匹配问题开始，逐步展开对其他形式的讨论。

6.8.1 入门示例：两个点集之间的最优匹配

假设存在两个点集 \(\left(\mathbf{x}_1, \ldots, \mathbf{x}_n\right)\) 和 \(\left(\mathbf{y}_1, \ldots, \mathbf{y}_n\right)\)， 每个集合包含取自集合 \(\mathcal{X}\) 的 \(n>1\) 个不同点。这两个点集之间的匹配是一种双射映射（bijective mapping）——将每个点 $\mathbf{x}_i$ 对应到另一个点 \(\mathbf{y}_j\)。 这种对应关系可通过配对索引 \((i, j) \in\{1, \ldots, n\}^2\) 来表示，这些索引定义了对称群（symmetric group） $\mathcal{S}_n$ 中的某种置换 $\sigma$。按照此约定，在给定置换 $\sigma$ 的情况下， $\mathbf{x}_i$ 将被对应到第二个点集中的第 $\sigma_i$ 个元素 \(\mathbf{y}_{\sigma_i}\)。

对称群 是一个数学概念，特指在抽象代数，特别是群论领域中，某个集合上所有可能的置换所构成的群。

匹配成本. 在将一个点集与另一个点集进行匹配时，自然需要考虑所有可能配对 \((i, j) \in\{1, \ldots, n\}^2\) 所产生的成本。例如， $\mathbf{x}_i$ 可能表示出租车司机 $i$ 的当前位置信息，而 \(\mathbf{y}_j\) 则对应刚发出用车请求的用户 $j$ 的位置；此时， \(C_{i j} \in \mathbb{R}\) 可以量化司机 $i$ 前往用户 $j$ 所需耗费的时间、燃油或距离成本。另一种场景中， \(\mathbf{x}_i\) 可能表示求职者 $i$ 所具备的技能向量， $\mathbf{y}_j$ 则代表胜任职位 $j$ 所需的技能向量；此时 \(C_{i j}\) 可量化员工 $i$ 完成工作 $j$ 所需的时间。

通常假设成本 $C_{i j}$ 是在点对 \(\left(\mathbf{x}_i, \mathbf{y}_j\right)\) 上计算成本函数 \(c: \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}\) 得到的，即 \(C_{i j}=c\left(\mathbf{x}_i, \mathbf{y}_j\right)\)。 在最优传输的多数应用中，成本函数通常具有几何意义，一般表现为在 $\mathcal{X}$ 上的距离函数（如图 6.18 中 \(\mathcal{X}=\mathbb{R}^2\) 的情形），关于这一点，我们将在 6.8.2.4 节进一步讨论。

最小成本匹配. 在给定成本函数 $c$ 的前提下，最优匹配（或分配）问题旨在找到一个能使总成本最小的置换方案，该总成本由以下函数定义：

\[\min _\sigma E(\sigma)=\sum_{i=1}^n c\left(\mathbf{x}_i, \mathbf{y}_{\sigma_i}\right) \tag{6.191}\]

最优匹配问题是最简单的组合优化问题之一，其研究最早可追溯至19世纪[JB65]。尽管通过穷举所有置换方案需要计算 $n!$ 次目标函数 $E$，但匈牙利算法[Kuh55]被证明能在多项式时间内求得最优解[Mun57]，后续改进版本在最坏情况下仅需 $O\left(n^3\right)$ 次运算。

6.8.2 从最优匹配到Kantorovich（坎托罗维奇）和Monge（蒙日）形式

最优匹配问题虽应用于众多场景，但存在若干局限。可以说，最优传输理论的大部分研究都是为了克服这些局限性，或者说是为了将式(6.191)推广至更一般的场景。最容易想到的局限是当两个点集的大小规模不同时该如何处理。第二个局限性出现在连续场景下——当需要匹配（或变换）的是两个概率密度函数而非原子化的离散集合。

6.8.2.1 质量分割（Mass splitting）

假设点 \(\mathbf{x}_i\) 和 \(\mathbf{y}_j\) 表示技能向量—— $\mathbf{x}_i$ 代表工人 $i$ 掌握的技能， \(\mathbf{y}_j\) 表示完成任务 $j$ 所需的技能。由于寻找匹配等价于在 \(\{1, \ldots, n\}\) 中寻找某种置换，因此问题(6.191)无法处理工人数量大于（或小于）任务数量的情况。更严重的是，匹配问题假设每个任务是不可分割的，且工人只能专职于单一任务，这种设定显然不符合实际。在现实中，某些任务可能需要投入多于（或少于）一名工人的工作量，而有些工人或许只能兼职工作，或者相反愿意加班。匹配问题中的置换是刚性的，无法处理这种情况。因为根据定义，置换是一一对应的关联。Kantorovich形式允许质量可分割，即工人提供的努力或完成给定任务所需的工作量是可以被分割的。在符号表达方面，除了 $\mathbf{x}_i$ 之外，还为每名工人（共 $n$ 名）关联一个正数 \(\mathbf{a}_i>0\)， 该数字表示工人 $i$ 能够提供的工作时间。类似地，我们引入数字 \(\mathbf{b}_j>0\) 来描述完成某项任务（共 $m$ 项）所需的时间（ $n$ 和 $m$ 不一定相等）。因此，工人 $i$ 被表示为 \(\left(\mathbf{a}_i, \mathbf{x}_i\right)\)， 在数学上等价于加权狄拉克测度 \(\mathbf{a}_i \delta_{\mathbf{x}_i}\)， 此时工厂可用的劳动力被定义为离散测度 \(\sum_i \mathbf{a}_i \delta_{\mathbf{x}_i}\)， 而其任务所需劳动力定义为 \(\sum_j \mathbf{b}_j \delta_{\mathbf{y}_j}\)。 如果进一步假设工厂的工作量是平衡的，即 \(\sum_i \mathbf{a}_i=\sum_j \mathbf{b}_j\)， 最优传输的Kantorovich[Kan42]形式为：

\[\mathrm{OT}_C(\mathbf{a}, \mathbf{b}) \triangleq \min _{P \in \mathbf{R}_{+}^{n \times m}, P\textbf{1}_n=\mathbf{a}, P^T \mathbf{1}_m=\mathbf{b}}\langle P, C\rangle \triangleq \sum_{i, j} P_{i j} C_{i j} . \tag{6.192}\]

耦合矩阵 $P$ 的含义很简单：每个系数 $P_{i j}$ 表示工人 $i$ 分配给任务 $j$ 的时间。第 $i$ 行的和必须等于 $\mathbf{a}_i$，以满足工人 $i$ 的时间约束；而第 $j$ 列的和必须等于 $\mathbf{b}_j$，表示完成任务 $j$ 所需的时间已被分配到位。

6.8.2.2 Monge形式与最优前推映射

通过引入质量分割，最优传输的Kantorovich形式使得不同规模和权重的离散测度之间能够进行更为通用的比较（图6.18中间图）。然而，这种灵活性也带来一个缺点：无法再像经典匹配问题那样，将每个点 $\mathbf{x}_i$ 唯一对应到另一个点 $\mathbf{y}_j$。有趣的是，当测度趋于连续的密度函数时，这一特性得以恢复。实际上，最优传输的Monge[Mon81]形式可以精准重现该特性，前提是（粗略地说）测度 $\mu$ 具有密度函数。在此设定下，确保 $\mu$ 能映射到 $\nu$ 的数学对象被称为前推（push forward）映射——即将 $\mu$ 转换为 $\nu$ 的映射 $T$。其定义为：对于任意可测集 $A \subset \mathcal{X}$，满足 $\mu\left(T^{-1}(A)\right)=\nu(A)$。当 $T$ 可微且 $\mu$, $\nu$ 关于 $\mathbb{R}^d$ 上的勒贝格测度具有密度函数 $p$ 和 $q$ 时，根据变量替换公式，该条件几乎处处等价于：

\[q(T(x))=p(x)\left|J_T(x)\right|, \tag{6.193}\]

其中 \(\left|J_T(x)\right|\) 表示 $T$ 的雅可比矩阵在 $x$ 处的行列式。

当映射 $T$ 满足这些条件时（记作 $T_{\sharp} \mu=\nu$），Monge [Mon81] 问题变成寻找最优映射 $T$，以最小化点 $\mathbf{x}$ 与其变换 $T(\mathbf{x})$ 之间的平均成本：

\[\inf _{T: T_{\sharp} \mu=\nu} \int_{\mathcal{X}} c(\mathbf{x}, T(\mathbf{x})) \mu(\mathrm{d} \mathbf{x}) . \tag{6.194}\]

因此，$T$ 是一个将 $\mu$ 整体推进到 $\nu$ 的映射，同时能实现最小的推进成本。尽管Monge问题非常直观，但由于其非凸性，在实践中求解极为困难。事实上，容易验证，约束条件 ${T_{\sharp} \mu=\nu}$ 不具有凸性，因为可以轻易找到反例：即使 $T_{\sharp} \mu=\nu$ 且 $T_{\sharp}^{\prime}\mu= \nu$，也未必满足 $\left(\frac{1}{2} T+\frac{1}{2} T^{\prime}\right)_{\sharp} \mu = \nu$。幸运的是，Kantorovich的方法同样适用于连续测度，并能转化为相对简单得多的线性规划问题。

“长度”、“面积”、“体积”这些我们熟悉的概念，本质上就是测度。测度就是一个数学工具，用来给一个集合（比如线段上的点集、平面上的区域）分配一个非负的数值，来表示这个集合的“大小”。所以，最通俗的理解是：测度就是“大小”的通用说法。
上文的测度指的就是一个概率分布。它可以很复杂，比如是离散的几个点（每个点有质量），也可以是绝对连续的，像一片“概率云”。

6.8.2.3 Kantorovich 形式

Kantorovich 问题（式6.192）同样可以扩展到连续场景：优化空间不再是 $\mathbb{R}^{n \times m}$ 空间的矩阵子集，而是 $\Pi(\mu, \nu)$ ——即具有边缘分布 $\mu$ 和 $\nu$ 的联合概率分布 $\mathcal{P}(\mathcal{X} \times \mathcal{X})$ 的子集：

\[\Pi(\mu, \nu) \triangleq\left\{\pi \in \mathcal{P}\left(\mathcal{X}^2\right): \forall A \subset \mathcal{X}, \pi(A \times \mathcal{X})=\mu(A) \text { and } \pi(\mathcal{X} \times A)=\nu(A)\right\} \tag{6.195}\]

需要注意的是 $\Pi(\mu, \nu)$ 是非空集合，因为它始终包含乘积测度 $\mu \otimes \nu$。基于该定义，(6.192) 的连续版本形式为：

\[\mathrm{OT}_c(\mu, \nu) \triangleq \inf _{\pi \in \Pi(\mu, \nu)} \int_{\mathcal{X}^2} c \mathrm{~d} \pi \tag{6.196}\]

其中 $\mathrm{OT}_c(\mu, \nu)$ 表示在成本函数 $c$ 下，从分布 $\mu$ 到 $\nu$ 的最优传输代价，$\inf$ 表示下确界或最小值。请注意，式 (6.196) 直接包含式 (6.192) ，因为当 $\mu$ 和 $\nu$ 是离散测度时——分别具有概率权重 $\textbf{a}$ 和 $\textbf{b}$ 以及位置 $\left(\mathbf{x}_1, \ldots, \mathbf{x}_n\right)$ 和 $\left(\mathbf{y}_1, \ldots, \mathbf{y}_m\right)$——可以验证这两个公式是等价的。

6.8.2.4 Wasserstein distances

当成本函数 $c$ 等于某个整数次幂的度量 $d$ 时，Kantorovich问题的最优解被称为测度 $\mu$ 与 $\nu$ 之间的Wasserstein距离：

\[W_p(\mu, \nu) \triangleq\left(\inf _{\pi \in \Pi(\mu, \nu)} \int_{\mathcal{X}^2} d(\mathbf{x}, \mathbf{y})^p \mathrm{~d} \pi(\mathbf{x}, \mathbf{y})\right)^{1 / p} \tag{6.197}\]

尽管在 $d$ 是度量的前提下，证明 $W_p(\mu, \nu)$ 的对称性以及 $W_p(\mu, \nu)=0 \Rightarrow \mu=\nu$ 这一性质相对容易，但证明三角不等式则略显困难，其证明需要基于一个称为“粘合引理”的结果（[Vil08, p.23]）。$W_p(\mu, \nu)$的 $p$ 次幂常被简写为$W_p^p(\mu, \nu)$。

6.8.3 最优传输的求解

6.8.3.1 对偶性和损失的凹形

式（6.192）和（6.196）都是线性规划问题：它们的约束条件和优化目标都只涉及到求和。在这种情况下，它们对应一个对偶形式（此处，再一次的，式(6.199) 包含 (6.198)）：

\[\max _{\substack{\mathbf{f} \in \mathbb{R}^n, \mathbf{g} \in \mathbb{R}^m \\ \mathbf{f} \oplus \mathbf{g} \leq C}} \mathbf{f}^T \mathbf{a}+\mathbf{g}^T \mathbf{b} \tag{6.198}\] \[\sup _{f \oplus g \leq c} \int_{\mathcal{X}} f \mathrm{~d} \mu+\int_{\mathcal{X}} g \mathrm{~d} \nu \tag{6.199}\]

其中符号 $\oplus$ 表示向量之间的张量加法， \(\mathbf{f} \oplus \mathbf{g}=\left[\mathbf{f}_i+\mathbf{g}_j\right]_{i j}\)， 或者函数 \(f \oplus g: \mathbf{x}, \mathbf{y} \mapsto f(\mathbf{x})+g(\mathbf{y})\)。 换言之，对偶问题旨在寻找一对向量（或函数），使其在作用于 \(\textbf{a}\) 和 \(\textbf{b}\) （或对 $\mu$ , $\nu$ 进行积分）时能获得尽可能高的期望值，但前提是这对向量（或函数）在任意两点 \(\textbf{x}\), \(\textbf{y}\) 之间的差异（以成本函数 $c$ 衡量）不能过大。

(6.192)和(6.196)中的对偶问题均包含两个变量。若聚焦于连续形式，经过仔细考察可以发现：在给定对应于第一个测度的函数 $f$ 后，我们能够计算出函数 $g$ 的最佳候选形式。该函数 $g$ 需在满足对所有 $\mathbf{x}$，$\mathbf{y}$ 均成立的不等式 $g(\mathbf{y}) \leq c(\mathbf{x}, \mathbf{y})-f(\mathbf{x})$ 的前提下尽可能取最大值，这使得

\[\forall \mathbf{y} \in \mathcal{X}, \bar{f}(\mathbf{y}) \triangleq \inf _{\mathbf{x}} c(\mathbf{x}, \mathbf{y})-f(\mathbf{x}), \tag{6.200}\]

是最优的选择。$\bar{f}$ 被称为 $f$ 的 $c$ 变换。当然，我们也可以选择从函数 $g$ 出发，来定义一个对应的 $c$ 变换：

\[\forall \mathbf{x} \in \mathcal{X}, \widetilde{g}(\mathbf{x}) \triangleq \inf _{\mathbf{y}} c(\mathbf{x}, \mathbf{y})-g(\mathbf{y}) \tag{6.201}\]

由于这些变换只能使解得到改进，我们甚至可以设想对任意函数 $f$ 交替施用这些变换，从而定义 $\bar{f}$、$\widetilde{\bar{f}}$ 等一系列函数。然而可以证明，这种做法意义有限，因为

\[\bar{\widetilde{\bar{f}}}=\bar{f} . \tag{6.202}\]

尽管如此，这一论述使得我们可以将候选函数的范围缩小到那些已经经历过此类变换的函数。这一推理引出了所谓的c-凹函数集，即 $\mathcal{F}_c \triangleq{f \mid \exists g: \mathcal{X} \rightarrow \mathbb{R}, f=\widetilde{g}}$。该集合可等价地证明为满足 $f=\tilde{\bar{f}}$ 的函数集。因此，我们可以将注意力集中在c-凹函数上，通过所谓的半对偶形式来求解(6.199)。

\[\sup _{f \in \mathcal{F}_c} \int_{\mathcal{X}} f \mathrm{~d} \mu+\int_{\mathcal{X}} \bar{f} \mathrm{~d} \nu \tag{6.203}\]

从(6.199)式到(6.203)式的推导过程中，我们消除了一个对偶变量 $g$，并将可行解集缩小至 $\mathcal{F}_c$ 集合，但代价是引入了高度非线性的变换 $\bar{f}$。然而这种重构具有重要价值——它使我们可以将研究范围限定在 $c$-凹函数领域，尤其适用于两类关键的成本函数 $c$：距离函数与平方欧几里得范数。

6.8.3.2 Kantorovich-Rubinstein 对偶性与 Lipschitz 势函数

一个能体现 c-凹性价值的重要结论出现在当 $c$ 为度量 $d$ 时，即 (6.197) 式中 $p=1$ 的情况。此时可以证明（尤其需要利用 $d$ 的三角不等式）：一个 d-凹函数 $f$ 是 1-利普希茨的（即对任意 $\mathbf{x}$, $\mathbf{y}$ 均有 $|f(\mathbf{x})-f(\mathbf{y})| \leq d(\mathbf{x}, \mathbf{y})$），且满足 $\bar{f}=-f$。 这一结论可转化为如下恒等式：

\[W_1(\mu, \nu)=\sup _{f \in 1 \text {-Lipschitz }} \int_{\mathcal{X}} f(\mathrm{~d} \mu-\mathrm{d} \nu) . \tag{6.204}\]

该结论具有众多实际应用。在低维情形中，可通过密度函数的小波系数有效逼近这个关于 1-利普希茨函数的上确界[SJ08]；在更一般情形中，则可采用启发式方法，通过训练参数化满足 1-利普希茨条件的神经网络来实现（使用 ReLU 激活函数并对权重矩阵元素施加约束）[ACB17]。

6.8.3.3 蒙日映射作为凸函数梯度：布雷尼耶定理

c-凹性的另一个应用出现在 $c(\mathbf{x}, \mathbf{y})=\frac{1}{2}|\mathbf{x}-\mathbf{y}|^2$ 的情形，该代价函数（相差一个常数因子）对应于欧氏空间中密度函数间使用的平方 $W_2$ 距离。[Bre91] 首次证明的卓越结论表明：对于该代价函数，求解两个测度间最优传输问题（6.194）的蒙日映射（假设 ( $\mu$ ) 足够正则，此处假定其对勒贝格测度具有密度）不仅存在，而且必然是一个凸函数的梯度。简言之，可以证明

\[T^{\star}=\arg \min _{T: T_{\sharp} \mu=\nu} \int_{\mathcal{X}} \frac{1}{2}\|\mathbf{x}-T(\mathbf{x})\|_2^2 \mu(\mathrm{~d} \mathbf{x}) \tag{6.205}\]

存在，且是某个凸函数 $u: \mathbb{R}^d \rightarrow \mathbb{R}$ 的梯度，即 $T^{\star}=\nabla u$。反之，对任意凸函数 $u$，连接 $\mu$ 与位移测度 $\nabla u_\text{#} \mu$ 的最优传输映射必等于 $\nabla u$。

我们给出证明概要：对于任何合理的代价函数 $c$（例如下有界且下半连续），总可利用原始-对偶关系：考虑 (6.196) 的最优耦合\(P^*\)以及 (6.203) 的最优 c-凹对偶函数\(f^*\)。这意味着 \((f^*, g^* = \overline{f^*})\) 是 (6.199) 的最优解。该线性规划对的互补松弛条件表明：若 \(\mathbf{x}_0, \mathbf{y}_0\) 位于 \(P^*\) 的支撑集中，则必然（且充分）有 \(f^*(\mathbf{x}_0) + \overline{f^*}(\mathbf{y}_0) = c(\mathbf{x}_0, \mathbf{y}_0)\)。 现假设 \(\mathbf{x}_0, \mathbf{y}_0\) 确实属于 \(P^*\) 的支撑集。由等式 \(f^*(\mathbf{x}_0) + \overline{f^*}(\mathbf{y}_0) = c(\mathbf{x}_0, \mathbf{y}_0)\) 可直接推得 \(\overline{f}^*(\mathbf{y}_0) = c(\mathbf{x}_0, \mathbf{y}_0) - f^*(\mathbf{x}_0)\)。 但根据定义， \(\overline{f}^*(\mathbf{y}_0) = \inf_{\mathbf{x}} c(\mathbf{x}, \mathbf{y}_0) - f^*(\mathbf{x})\)。 因此，$\mathbf{x}_0$ 具有特殊性质：它最小化 \(\mathbf{x} \to c(\mathbf{x}, \mathbf{y}_0) - f^*(\mathbf{x})\)。 若注意到本节假设 \(c(\mathbf{x}, \mathbf{y}) = \frac{1}{2}\|\mathbf{x} - \mathbf{y}\|^2\)， 则 $\mathbf{x}_0$ 满足

\[\mathbf{x}_0 \in \underset{\mathbf{x}}{\operatorname{argmin}} \frac{1}{2}\left\|\mathbf{x}-\mathbf{y}_0\right\|^2-f^{\star}(\mathbf{x}) \tag{6.206}.\]

假设 $f^*$ 可微（这可通过 c-凹性证明），则得到恒等式

\[\mathbf{y}_0-\mathbf{x}_0-\nabla f^{\star}\left(\mathbf{x}_0\right)=0 \Rightarrow \mathbf{y}_0=\mathbf{x}_0-\nabla f^{\star}\left(\mathbf{x}_0\right)=\nabla\left(\frac{1}{2}\|\cdot\|^2-f^{\star}\right)\left(\mathbf{x}_0\right) . \tag{6.207}\]

因此，若 $(\mathbf{x}_0, \mathbf{y}_0)$ 属于 \(P^*\) 的支撑集，则 $\mathbf{y}_0$ 被唯一确定，这证明 $P^*$ 实际上是伪装成耦合的蒙日映射，即

\[P^{\star}=\left(\operatorname{Id}, \nabla\left(\frac{1}{2}\|\cdot\|^2-f^{\star}\right)\right)_{\sharp} \mu . \tag{6.208}\]

证明的剩余部分可推导如下：对任意函数 $h : \mathcal{X} \to \mathbb{R}$，利用 c-变换和勒让德变换的定义可证明，$\frac{1}{2}|\cdot|^2 - h$ 是凸函数当且仅当 $h$ 是 c-凹函数。该证明的中间步骤依赖于证明 $\frac{1}{2}|\cdot|^2 - \overline{h}$ 等于 $\frac{1}{2}|\cdot|^2 - h$ 的勒让德变换。因此，由 \(f^*\) 的 c-凹性可知函数 \(\frac{1}{2}\|\cdot\|^2 - f^*\) 是凸函数，而最优传输映射本身即是凸函数的梯度。

认识到平方欧几里得代价的最优传输映射必为凸函数梯度这一事实，对求解 (6.203) 极具价值。此认知可用于将估计范围限制在相关的函数族中，例如 [AXX17] 提出的输入凸神经网络的梯度，或如 [Mak+20] 与 [Kor+20] 所建议的方法，以及具有理想光滑性和强凸性常数的任意凸函数 [PdC20]。

6.8.3.4 单变量与高斯分布的闭式解

许多概率分布间的度量在简单情形下都具有闭式表达式。瓦瑟斯坦距离也不例外，在两种重要场景下可以精确计算闭式解：当分布是单变量且代价函数 $ c(x,y) $ 是差值 $ x-y $ 的凸函数时，或者当 $ \partial c/\partial x \partial y < 0 $ 几乎处处成立时，瓦瑟斯坦距离本质上就是 $ \mu $ 与 $ \nu $ 的分位函数之间的比较。需要说明的是，对于一个测度 $ \rho $，其分位函数 $ Q_\rho $ 是定义域为 $ [0,1] $ 且值域为 $ \rho $ 支撑集的函数，它对应于 $ \rho $ 的累积分布函数 $ F_\rho $ 的（广义）逆映射。基于这些符号约定，我们可以得到：

\[\mathrm{OT}_c(\mu, \nu)=\int_{[0,1]} c\left(Q_\mu(u), Q_\nu(u)\right) \mathrm{d} u \tag{6.209}\]

特别地，当代价函数 $c$ 为 $(x,y) \mapsto |x - y|$ 时， $OT_1(\mu,\nu)$ 对应于柯尔莫哥洛夫-斯米尔诺夫统计量，即 $\mu$ 与 $\nu$ 的累积分布函数之间的面积。若 $c$ 取 $(x,y) \mapsto (x - y)^2$，我们得到的就是 $\mu$ 与 $\nu$ 的分位函数间的平方欧几里得范数。最后值得注意的是，此时蒙日映射也存在闭式解，其表达式为 $Q_\nu \circ F_\mu$。

第二种闭式解适用于所谓椭圆轮廓分布，其中最主要的是多元高斯分布[Gel90]。对于两个高斯分布 $\mathcal{N}(m_1, \Sigma_1)$ 和 $\mathcal{N}(m_2, \Sigma_2)$，它们的 2-瓦瑟斯坦距离可分解为：

\[W_2^2\left(\mathcal{N}\left(\mathbf{m}_1, \Sigma_1\right), \mathcal{N}\left(\mathbf{m}_2, \Sigma_2\right)\right)=\left\|\mathbf{m}_1-\mathbf{m}_2\right\|^2+\mathcal{B}^2\left(\Sigma_1, \Sigma_2\right) \tag{6.210}\]

其中 Bures 度量 $\mathcal{B}$ 定义为：

\[\mathcal{B}^2\left(\Sigma_1, \Sigma_2\right)=\operatorname{tr}\left(\Sigma_1+\Sigma_2-2\left(\Sigma_1^{\frac{1}{2}} \Sigma_2 \Sigma_1^{\frac{1}{2}}\right)^{\frac{1}{2}}\right) \tag{6.211}\]

特别需要注意的是，即使协方差矩阵不可逆，这些量值仍然有明确的定义；而当两个协方差矩阵都趋近于零时，该距离会收敛为均值间的距离。当第一个协方差矩阵可逆时，其最优蒙日映射由以下表达式给出：

\[T \triangleq \mathbf{x} \mapsto A\left(\mathbf{x}-\mathbf{m}_1\right)+\mathbf{m}_2, \text { where } A \triangleq \Sigma_1^{-\frac{1}{2}}\left(\Sigma_1^{\frac{1}{2}} \Sigma_2 \Sigma_1^{\frac{1}{2}}\right)^{\frac{1}{2}} \Sigma_1^{-\frac{1}{2}} \tag{6.212}\]

很容易证明 $T^*$ 确实是最优映射：$T$ 将高斯分布 $\mathcal{N}(\mathbf{m}_1, \Sigma_1)$ 推前为 $\mathcal{N}(\mathbf{m}_2, \Sigma_2)$ 这一事实，源于高斯分布的仿射推前仍是高斯分布的性质。此处设计的 $T$ 精确地将第一个高斯分布推前为第二个高斯分布（其中 $A$ 的设计使得从方差为 $\Sigma_1$ 的随机变量出发，能还原出方差为 $\Sigma_2$ 的随机变量）。$T$ 的最优性可通过以下观察得以证明：由于 $A$ 是正定矩阵，该映射是一个凸二次函数的梯度，通过套用上述布雷尼耶定理即可完成证明。

6.8.3.5 使用线性规划求解器精确求解

我们曾通过对偶性和 $c$-凹性暗示，当 $c$ 为欧氏距离或其平方时，可采用基于 1-利普希茨或凸神经网络的随机优化方法来估计瓦瑟斯坦距离。然而，这些方法是非凸的，只能达到局部最优解。除上述两种情况及前文提供的闭式解外，计算瓦瑟斯坦距离的唯一可靠方法出现在 $\mu$ 和 $\nu$ 均为离散测度时：此时可通过实例化并求解离散形式的 (6.192) 问题或其对偶形式 (6.198) 来实现。该原始问题是网络流问题的典型范例，可通过网络单纯形法以 $O(nm(n+m)\log(n+m))$ 的复杂度求解 [AMO88]，或采用与之相当的拍卖算法 [BC89]。但这些方法存在计算局限性：其立方级计算成本在大规模场景下难以承受；其组合特性使得在共享成本矩阵 $C$ 的情况下，难以并行求解多个最优传输问题。

另一个源于统计学的根本性问题进一步限制了这些线性规划 formulations 的应用，尤其是在高维场景中。实践者使用 (6.192) 时最可能遇到的瓶颈是：在多数情况下，他们的目标是通过包含在经验测度 $\hat{\mu}_n, \hat{\nu}_n$ 中的独立同分布样本来逼近两个连续测度 $\mu, \nu$ 间的距离。使用 (6.192) 来逼近对应的 (6.196) 注定会失败，正如多项研究 [FG15] 在相关设定（特别是 $\mathbb{R}^q$ 空间中的测度）中所证明的，(6.192) 提供的估计量逼近 (6.196) 的样本复杂度量级为 $1/n^{1/q}$。换言之，$W_2(\mu, \nu)$ 与 $W_2(\hat{\mu}_n, \hat{\nu}_n)$ 之间的差距在期望意义下很大，且在高维空间中随着 $n$ 的增加衰减极其缓慢。因此对这些样本精确求解 (6.196) 无异于浪费时间进行过拟合。为应对这一维度灾难，在实践中极有必要采用更谨慎的策略来处理 (6.196)，即通过引入能利用 $\mu$ 和 $\nu$ 先验假设的正则化方法。虽然前述所有基于神经网络的方法都可在此视角下解读，接下来我们将重点关注一种能产生凸优化问题的特定方法，该方法实现相对简单，具有极佳的并行性，且仅需二次复杂度。

6.8.3.6 利用熵正则化获得光滑性

[Cut13] 在早期研究 [Wil69; KY94] 的基础上，并借鉴了当 $c = d^2$ 时与薛定谔桥问题的渊源 [Léo14]，提出了一种加速求解 (6.192) 的计算方法。该方法的核心理念是通过引入耦合分布与边缘分布乘积 $\mu \otimes \nu$ 之间的 Kullback-Leibler 散度来正则化传输代价。

\[W_{c, \gamma}(\mu, \nu) \triangleq \inf _{\pi \in \Pi(\mu, \nu)} \int_{\mathcal{X}^2} d(\mathbf{x}, \mathbf{y})^p \mathrm{~d} \pi(\mathbf{x}, \mathbf{y})+\gamma D_{\mathrm{KL}}(\pi \| \mu \otimes \nu) \tag{6.213}\]

当在离散测度上实例化时，该问题等价于以下关于传输矩阵集的 $\gamma$-强凸问题（应与(6.192)式对比）：

\[OT_{C,\gamma}(\mathbf{a}, \mathbf{b}) = \min_{P \in R^{n \times m}_{+}, P1_{m} = \mathbf{a}, P^T1_{n} = \mathbf{b}} \langle P, C \rangle \triangleq \sum_{i,j} P_{ij} C_{ij} - \gamma \mathbb{H}(P) + \gamma (\mathbb{H}(\mathbf{a}) + \mathbb{H}(\mathbf{b})) , \tag{6.214}\]

该问题本身又等价于以下对偶问题（应与(6.198)式对比）：

\[OT_{C,\gamma}(\mathbf{a}, \mathbf{b}) = \max_{\mathbf{f} \in R^{n}, \mathbf{g} \in R^{m}} \mathbf{f}^{T} \mathbf{a} + \mathbf{g}^{T} \mathbf{b} - \gamma (e^{\mathbf{f}/\gamma})^{T} K e^{\mathbf{g}/\gamma} + \gamma (1 + \mathbb{H}(\mathbf{a}) + \mathbb{H}(\mathbf{b})) \tag{6.215}\]

其中 \(K \triangleq e^{-C/\gamma}\) 是 $-C/\gamma$ 的逐元素指数函数。这种正则化具有多重优势。原始-对偶关系揭示了（唯一）解 $P^{*}_{\gamma}$ 与最优对偶变量 \((\mathbf{f}^{*}, \mathbf{g}^{*})\) 之间的显式联系：

\[P^{*}_{\gamma} = \text{diag}(e^{\mathbf{f}/\gamma}) K \text{diag}(e^{\mathbf{g}/\gamma}) \tag{6.216}\]

问题(6.215)可采用实践中证明非常稳健的简单策略求解：通过简单的块坐标上升法（交替优化 $\mathbf{f}$ 和 $\mathbf{g}$ 的目标函数），得到著名的Sinkhorn算法[Sin67]。此处使用对数-求和-指数更新公式，从任意初始化的 $\mathbf{g}$ 出发，依次执行这两个更新直至收敛：

\[\mathbf{f} \leftarrow \gamma \log \mathbf{a} - \gamma \log K e^{\mathbf{g}/\gamma} \quad \mathbf{g} \leftarrow \gamma \log \mathbf{b} - \gamma \log K^{T} e^{\mathbf{f}/\gamma} \tag{6.217}\]

该算法的收敛性已得到充分研究（参见[CK21]及其参考文献）。随着 $\gamma$ 减小，收敛速度自然变慢，这反映了逼近线性规划解的难度，如[AWR17]所研究。这种正则化还具有统计优势，因为如[Gen+19]所述，正则化瓦瑟斯坦距离的样本复杂度提升至 $O(1/\sqrt{n})$ 量级，但其常数项 $1/\gamma^{q/2}$ 会随着维度增加而恶化。