5 信息论

本章，我们介绍信息论。KL散度衡量了两个分布之间的相似度，但从信息论的角度看，KL散度又被称为信息增益。为什么？本质上，KL散度衡量了从一个分布更新到另一个分布所需要的信息量。所以它属于两个分布互相变换过程中的信息增益。

• 5.1 KL散度
  • 5.1.1 理想条件
  • 5.1.2 KL散度唯一满足上述条件
    • 5.1.2.1 KL的连续性
    • 5.1.2.2 KL 的非负性
    • 5.1.2.3 KL散度对重参数具有不变形
    • 5.1.2.4 均匀分布的单调性
    • 5.1.2.5 KL散度的链式法则
  • 5.1.3 关于KL散度的思考
    • 5.1.3.1 KL的单位
    • 5.1.3.2 KL散度的非对称性
    • 5.1.3.3 KL as expected weight of evidence
  • 5.1.4 最小化KL
    • 5.1.4.1 前向vs逆向KL
    • 5.1.4.2 Moment projection (mode covering)
    • 5.1.4.3 Information projection (mode seeking)
  • 5.1.5 KL的属性
    • 5.1.5.1 压缩引理
    • 5.1.5.2 KL的数据处理不等式
  • 5.1.6 KL散度和MLE
  • 5.1.7 KL散度和贝叶斯推断（这段比较难理解）
  • 5.1.8 KL散度和指数族
    • 5.1.8.1 案例：高斯分布之间的KL散度
  • 5.1.9 使用 Fisher 信息矩阵近似KL散度
  • 5.1.10 Bregman散度
    • 5.1.10.1 KL 散度是一个 Bregman 散度
• 5.2 熵（Entropy）
  • 5.2.1 定义
  • 5.2.2 连续随机变量的可微熵
  • 5.2.3 Typical sets（典型集）
  • 5.2.4 交叉熵和不确定性（perplexity）
• 5.3 互信息（Mutual information）
  • 5.3.1 定义
  • 5.3.2 解释
  • 5.3.3 数据处理不等式（Data processing inequality）
  • 5.3.4 充分统计量
  • 5.3.5 多个变量之间的互信息
    • 5.3.5.1 完全相关性
    • 5.3.5.2 交互信息（Interaction information， co-information）
    • 5.3.5.3 协同效应与冗余
    • 5.3.5.4 MMI 和因果
    • 5.3.5.5 MMI和熵
  • 5.3.6 互信息的变分确界
    • 5.3.6.1 上确界
    • 5.3.6.2 BA下确界
    • 5.3.6.3 NWJ下确界
    • 5.3.6.4 InfoNCE下确界
  • 5.3.7 Relevance networks
• 5.4 数据压缩（Data compression (source coding)）
  • 5.4.1 无损压缩
  • 5.4.2 有损压缩和率失真权衡(here)
  • 5.4.3 Bits back 编码
• 5.5 误差-矫正编码（信道编码）
• 5.6 信息瓶颈（The information bottleneck）
  • 5.6.1 基础版的信息瓶颈
  • 5.6.2 变分 IB
  • 5.6.3 条件熵瓶颈
• 5.7 算法信息论
  • 5.7.1 柯尔莫哥洛夫复杂度（Kolmogorov Complexity）
  • 5.7.2 所罗门诺夫归纳（Solomonoff Induction）
  • 5.7.3 AIXI 和通用人工智能（AGI）

机器学习的核心在于信息处理（information processing）。那什么是信息？我们又该如何衡量信息？归根结底，我们需要一种方法来量化从一组信念（或者理解成概率分布）到另一组信念的更新幅度，我们之所以更新信念（概率分布），往往是因为我们获得了额外的信息，所以量化更新的幅度，等价地量化了获得的信息本身¹。这种量化方式应该满足一些预期的属性，事实证明，Kullback-Leibler (KL) 散度是唯一满足这些属性的度量方式（见第 5.1 节）。我们将研究 KL 散度的性质及其两种特殊情况：熵（第 5.2 节）和互信息（第 5.3 节），它们足够重要以至于值得独立研究。接下来，我们将简要讨论信息论的两个主要应用。第一个是数据压缩（data compression）（或称源编码（source coding）），即通过去除数据中的冗余信息使其能够以更紧凑的方式表达。数据压缩可以是无损的（例如 ZIP 文件），也可以是有损的（例如 MP3 文件），详情见第 5.4 节。第二个应用是纠错（error correction，或称信道编码，channel coding），即以某种方式对数据进行编码，使其在通过含噪的信道（例如电话线或卫星链路）传输时具有抗干扰的能力，详情见第 5.5 节。

事实证明，数据压缩以及纠错的实现都依赖于对数据进行准确的概率建模。在数据压缩中，概率模型使发送方能够为高频的数据向量分配更短的编码，从而节省存储空间。而在纠错的应用中，概率模型使接收方能够结合接收到的被干扰的信息和信息的先验分布，推断出最可能的原始消息。

显然，基于概率论的概率机器学习范式对信息论非常有用。然而，信息论对机器学习也同样重要。事实上，我们已经看到，贝叶斯机器学习的核心是表征和减少不确定性，而这本质上与信息有关。在第 5.6.2 节中，我们将更详细地探讨这一方向，讨论信息瓶颈。

关于信息论的更多内容，可以参考 [Mac03]²; [CT06]³ 等文献。

5.1 KL散度

本节内容由 Alex Alemi 合著。

在讨论信息论时，我们需要某种方法来衡量或量化“信息”本身。我们的分析从一个分布 $q(x)$ 开始，该分布描述了我们对某个随机变量的信念程度。接着，我们希望将这个信念更新到一个新的分布 $p(x)$，这种更新可能是因为我们展开了新的测量，或者对问题有了更深入的思考（获得了额外的信息）。我们想寻求一种数学方法来量化这一更新的幅度，并用 $I[p | q]$ 表示这个量。那么，这种度量应该满足哪些合理的属性要求呢？我们将在下文中讨论这个问题，并定义一个满足这些要求的量。

5.1.1 理想条件

为简单起见，假设我们描述的是一个包含 $N$ 个可能事件的分布。在这种情况下，概率分布 $q(\boldsymbol{x})$ 由 $N$ 个非负实数组成，且这些数的总和为 1。更具体地说，假设我们描述的随机变量是下一张从牌堆中抽出的牌的花色：$S\in${♣,♠,♡,♢}。假设一开始我们相信花色的分布是均匀的：$q = \left[\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right]$。接下来，如果朋友告诉我们所有的红色牌已经从牌堆中被移除了，我们可以将信念更新为： $q’ = \left[\frac{1}{2}, \frac{1}{2}, 0, 0\right]$。或者，我们可能相信牌堆中的一些方块牌变成了梅花，那此时的分布可以更新为：$q’’ = \left[\frac{3}{8}, \frac{2}{8}, \frac{2}{8}, \frac{1}{8}\right]$。那么，是否有一种好的方法来量化我们关于信念更新的幅度呢？哪个更新的幅度更大呢：$q \to q’$ 还是 $q \to q’’$？

任何有用的度量都应该满足以下特性：

1. 对参数的连续性：如果我们对起始分布或终止分布进行微小的扰动，那么更新幅度的变化也应该相应地很小。例如，对于 $q = \left[\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right]$，当 $\epsilon$ 很小时，$I\left[p \parallel \left(\frac{1}{4} + \epsilon, \frac{1}{4}, \frac{1}{4}, \frac{1}{4} - \epsilon\right)\right]$ 应该接近于 $I[p \parallel q]$。

2. 非负性：对于所有的 $p(\boldsymbol{x})$ 和 $q(\boldsymbol{x})$，都有 $I[p \parallel q] \geq 0$。更新幅度应始终为非负值。

3. 置换不变性：更新幅度不应依赖于 $\boldsymbol{x}$ 中元素的顺序。例如，无论我按 ♣,♠,♡,♢ 的顺序列出花色的概率，还是按 ♣,♢,♡,♠ 的顺序，只要在所有分布中保持元素的顺序一致，结果应该是相同的。例如：$I[a, b, c, d \parallel e, f, g, h] = I[a, d, c, b \parallel e, h, g, f]$。

4. 对均匀分布的单调性：虽然一般情况下很难确定信念更新的幅度，但在某些特殊情况下我们可以有清晰的直觉。例如，如果我们的信念从 $N$ 个元素的均匀分布更新为 $N’$ 个元素的均匀分布，那么信息增益应该是关于 $N$ 的递增函数，同时是 $N’$ 的递减函数。例如，从所有四种花色的均匀分布 $[\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4} ]$（$N = 4$）更新到仅一种花色（如全是梅花）$[1, 0, 0, 0]$（$N’ = 1$）的更新幅度，比更新为仅黑色的花色 $[ \frac{1}{2}, \frac{1}{2}, 0, 0 ]$（$N’ = 2$）的更新幅度更大。

5. 满足自然链式法则：到目前为止，我们一直在描述对下一张抽牌结果的信念，这个信念是一个表示下一张牌花色的随机变量（$S\in${♣,♠,♡,♢}。我们也可以等效地将上述过程拆分成两个步骤。首先，考虑一个表示牌的颜色的随机变量（$C\in{\blacksquare，\square}$），其中黑色$\blacksquare$表示 {♣,♠}，红色$\square$表示 {♡,♢}。然后，如果我们抽到的是红色牌，然后进一步描述它是红心（♡）还是方块（♢）的概率分布；如果抽到的是黑色牌，然后进一步描述它是梅花（♣）还是黑桃（♠）的概率分布。这种方式可以将联合概率分布表示为关于花色的边际分布和以花色为条件的概率分布的因式分解形式，并且符合自然链式法则。比方说：

   \[p(S)=\left[\frac{3}{8}, \frac{2}{8}, \frac{2}{8}, \frac{1}{8}\right]\tag{5.1}\]

   拆分成

   \[p(C)=\left[\frac{5}{8}, \frac{3}{8}\right] \quad p(\{\clubsuit, \spadesuit\} \mid C=\blacksquare)=\left[\frac{3}{5}, \frac{2}{5}\right] \quad p(\{\heartsuit, \diamondsuit\} \mid C=\square)=\left[\frac{2}{3}, \frac{1}{3}\right] \tag{5.2}\]

​ 同样地，我们可以对均匀分布 $q$ 进行分解。显然，为了使我们的信息度量具有实用性，不论我们如何拆分同一个物理过程，信息更新的幅度需要保持一致。我们需要的是一种方法，将四种不同的信息增益关联起来：

\[\begin{align} & I_S \equiv I[p(S) \| q(S)] \tag{5.3}\\ & I_C \equiv I[p(C) \| q(C)] \tag{5.4}\\ & I_{\blacksquare} \equiv I[p(\{\clubsuit, \spadesuit\} \mid C=\blacksquare) \| q(\{\clubsuit, \spadesuit\} \mid C=\boldsymbol{\blacksquare})] \tag{5.5}\\ & I_{\square} \equiv I[p(\{\heartsuit, \diamondsuit\} \mid C=\square) \| q(\{\heartsuit, \diamondsuit\} \mid C=\square)] \tag{5.6} \end{align}\]

显然 $I_S$ 应该是关于 ${I_C, I_\blacksquare, I_\square}$ 的某个函数。所以，我们的最后一个理想条件是 $I_S$ 是 $I_C, I_\blacksquare, I_\square$ 的线性组合。具体而言，我们要求它们以加权线性组合的形式结合，其中权重根据分布 $p$ 决定：

\[I_S = I_C +p(C=\blacksquare)I_\blacksquare+p(C=\square)I_\square=I_C+\frac{5}{8}I_\blacksquare+\frac{3}{8}I_\square \tag{5.7}\]

更正式的表述为：如果我们将 $\boldsymbol{x}$ 拆分成两个部分 $[\boldsymbol{x}_L,\boldsymbol{x}_R]$，那么我们有 $p(\boldsymbol{x})=p\left(\boldsymbol{x}_L\right) p\left(\boldsymbol{x}_R \mid \boldsymbol{x}_L\right)$，同样 $q$ 也有类似的表达，那更新的幅度应该是

\[I[p(\boldsymbol{x}) \| \boldsymbol{q}(\boldsymbol{x})]=I\left[p\left(\boldsymbol{x}_L\right) \| q\left(\boldsymbol{x}_L\right)\right]+\mathbb{E}_{p\left(\boldsymbol{x}_L\right)}\left[I\left[p\left(\boldsymbol{x}_R \mid \boldsymbol{x}_L\right) \| q\left(\boldsymbol{x}_R \mid \boldsymbol{x}_L\right)\right]\right] \tag{5.8}\]

请注意，这一要求打破了两个分布之间的对称性：右侧要求我们根据边缘分布计算条件信息增益的期望，但我们需要决定以哪一个边缘分布来计算期望。

5.1.2 KL散度唯一满足上述条件

我们现在将定义一个满足上述所有要求（除一个乘法常数外）的唯一的度量。Kullback-Leibler 散度（或称为 KL 散度），也称为信息增益（information gain）或相对熵（relative entropy），其定义如下：

\[D_{\mathrm{KL}}(p \| q) \triangleq \sum_{k=1}^K p_k \log \frac{p_k}{q_k} \tag{5.9}\]

扩展到连续分布：

\[D_{\mathrm{KL}}(p \| q) \triangleq \int d x p(x) \log \frac{p(x)}{q(x)} \tag{5.10}\]

接下来，我们将验证此定义是否满足我们的所有要求。（例如，可以在[Hob69]⁴；[Rén61]⁵中找到证明它是满足这些属性的唯一度量的证据。）

5.1.2.1 KL的连续性

KL散度显然是连续的，除了两种情况需要额外考虑一下，即当 $p_k$ 或 $q_k$ 等于0的时候。首先考虑第一种情况，注意到当 $p \rightarrow 0$，KL的极限情况表现依然良好：

\[\lim _{p \rightarrow 0} p \log \frac{p}{q}=0 \tag{5.11}\]

将此作为$p=0$时被积函数的结果，将使KL在$p=0$处连续。问题在于当 $p \neq 0$ 而 $q=0$ 时。所以信息增益要求原始信念分布 $q$ 在更新分布 $p$ 有定义的任何地方同样有定义。直观上，将完全为 0 的信念（$q_k=0$）更新到某个正值（$p_k\gt0$），需要无穷的信息。

5.1.2.2 KL 的非负性

本节，我们将证明 KL 散度永远是非负的。这里将使用 琴森不等式（Jensen’s inequality），即，对于任意凸函数 $f$，我们有

\[f\left(\sum_{i=1}^n \lambda_i \boldsymbol{x}_i\right) \leq \sum_{i=1}^n \lambda_i f\left(\boldsymbol{x}_i\right) \tag{5.12}\]

其中 $\lambda_i \ge 0$，$\Sigma_{i=1}^n\lambda_i=1$。上式可以通过归纳法来证明，其中$n=2$的情况遵循凸性的定义。

定理5.1.1. （信息不等式）$D_{\mathrm{KL}}(p | q) \geq 0$ 当且仅当 $p=q$ 时，等号满足。

证明。沿用 [CT06]³ 的方法。正如我们在前文中提到的，KL散度需要额外考虑 $p(x)=0$ 或 $q(x)=0$ 的特殊情况，此处也一样。令 $A={x:p(x)\gt0}$ 表示 $p(x)$ 的支撑集。利用负对数函数是凸函数的性质和琴森不等式，我们有

\[\begin{align} -D_{\mathrm{KL}}(p \| q) & =-\sum_{x \in A} p(x) \log \frac{p(x)}{q(x)}=\sum_{x \in A} p(x) \log \frac{q(x)}{p(x)} \tag{5.13}\\ & \leq \log \sum_{x \in A} p(x) \frac{q(x)}{p(x)}=\log \sum_{x \in A} q(x) \tag{5.14}\\ & \leq \log \sum_{x \in \mathcal{X}} q(x)=\log 1=0 \tag{5.15} \end{align}\]

考虑到 $\log(x)$ 是严格凹函数（所以$-\log(x)$ 是凸函数），式（5.14）的不等式中等号成立的充要条件是 $p(x)=cq(x)$ ，其中常数 $c$ 用于表示整个空间 $\mathcal{X}$ 中集合 $A$ 所占的比例。公式（5.15）等号成立的充要条件是 $\sum_{x \in A} q(x)=\sum_{x \in \mathcal{X}} q(x)=1$，即 $c=1$。所以 $D_{\mathbb{KL}}(p | q)=0$ 的充要条件是对于所有的 $x$ ，满足 $p(x)=q(x)$。

KL 散度的非负性往往被认为是信息论中最有用的结论之一。每当你能够将一个表达式重新写成包含 KL 散度的形式时，由于 KL 散度保证是非负的，直接忽略相关项就能立即得到一个表达式的确界（bound）。

5.1.2.3 KL散度对重参数具有不变形

我们希望信息度量对标签的排列具有不变性。离散形式的信念显然具有置换不变性，就像求和一样。KL散度显然满足重参数不变性。换句话说，如果使用一个可逆映射对随机变量进行变换，这个过程并不会改变KL散度本身。

假设将随机变量 $x$ 映射到 $y=f(x)$ ，已知 $p(x) d x=p(y) d y$ 和 $q(x) d x=q(y) d y$。所以 KL 散度对于两个随机变量是相同的：

\[D_{\mathbb{KL}}(p(x) \| q(x))=\int d x p(x) \log \frac{p(x)}{q(x)}=\int d y p(y) \log \left(\frac{p(y)\left|\frac{d y}{d x}\right|}{q(y)\left|\frac{d y}{d x}\right|}\right)=D_{\mathbb{KL}}(p(y) \| q(y)) \tag{5.16}\]

由于这种重参数不变性，我们可以放心地认为，当我们衡量两个分布之间的KL散度时，我们衡量的是分布的某些特性，而不是变量所在的空间。因此，我们可以自由地将变量映射到便于分析的空间——例如图像的傅里叶空间——而不会影响结果。

5.1.2.4 均匀分布的单调性

考虑从一个包含 $N$ 个元素的均匀分布更新到一个包含 $N’$ 个元素的均匀分布。KL散度为：

\[D_{\mathbb{KL}}(p \| q)=\sum_k \frac{1}{N^{\prime}} \log \frac{\frac{1}{N^{\prime}}}{\frac{1}{N}}=\log \frac{N}{N^{\prime}} \tag{5.17}\]

上式也可以解释为更新前后元素数量比的对数。这满足单调性的要求。

我们可以这样解读这个结果：考虑通过二分法在一个已排序的数组中查找某个元素。一个设计良好的“是/否”问题可以将搜索空间一分为二。以比特为单位，KL散度告诉我们，从 $q$ 到 $p$ 平均需要多少个设计良好的“是/否”问题。

## 以下示例由 chatgpt 提供

假设你有一个已排序的数组：`[1, 3, 5, 7, 9, 11, 13, 15]`，你要通过二分法查找目标元素 `9`。

### 1. 二分法查找的过程：
- 首先，你会选择数组的中间元素 `7`，问：“目标值是 `7` 吗？”这个问题把搜索空间从 `8` 个元素减少到 `4` 个元素。
- 由于 `9 > 7`，你就知道目标元素一定在右半部分，因此你的新搜索空间变成了 `[9, 11, 13, 15]`。
- 接下来，你选择新的中间元素 `11`，问：“目标值是 `11` 吗？”再一次把搜索空间缩小。
- 因为 `9 < 11`，你就缩小搜索范围，剩下 `[9]`。
- 最后，你直接找到目标元素 `9`。

在这个过程中，你一共问了 3 个“是/否”问题：`7`、`11` 和 `9`，最终定位到了目标。

### 2. 使用KL散度来解释：
假设你的初始信念是目标在某个位置的概率分布，记作 `q`，而真实目标的位置是分布 `p`。在这个例子中：

- 假设你开始时并不清楚目标在哪里，所以可以假设每个位置上的概率相等（即 `q` 是均匀分布）。
- 真实目标值是 `9`，所以 `p` 是一个高度集中的分布，只有 `9` 这个位置的概率是1，其它位置的概率为0。

### 3. KL散度的作用：
KL散度量化了从你最初的均匀分布 `q` 到真实分布 `p` 的信息损失。在二分法中，每一次“是/否”问题，实际上都是通过更新概率分布来减少不确定性。在第一次询问中，你将 `q` 从均匀分布逐渐转变为一个更集中在右半部分的分布。在每个“是/否”问题之后，你逐步减少搜索空间，也就意味着你正逐步减少信息的不确定性。

KL散度会告诉你，在你最初的假设下，平均需要多少个“是/否”问题才能把你从均匀分布 `q` 的不确定状态，缩小到目标位置的确定状态 `p`。换句话说，KL散度是衡量你通过“是/否”问题来逼近目标位置的效率——如果问题设计得好，KL散度小，你能更快找到目标；如果问题设计不好，KL散度大，找到目标就会更慢。

### 总结：
- 在二分查找中，每次提问都相当于把搜索空间一分为二，从而逐步减少不确定性。
- KL散度通过衡量你从一个初始分布（比如均匀分布）到真实分布（目标位置）所需的平均“是/否”问题数量，帮助你理解这种信息收缩过程的效率。

5.1.2.5 KL散度的链式法则

此处，我们将介绍 KL 散度满足的自然链式法则：

\[\begin{align} D_{\mathbb{KL}}(p(x, y) \| q(x, y)) & =\int d x d y p(x, y) \log \frac{p(x, y)}{q(x, y)} \tag{5.18}\\ & =\int d x d y p(x, y)\left[\log \frac{p(x)}{q(x)}+\log \frac{p(y \mid x)}{q(y \mid x)}\right] \tag{5.19}\\ & =D_{\mathbb{KL}}(p(x) \| q(x))+\mathbb{E}_{p(x)}\left[D_{\mathbb{KL}}(p(y \mid x) \| q(y \mid x))\right] . \tag{5.20} \end{align}\]

所以，实际上我们将分布分解为对应的条件分布形式，而KL散度直接可以相加。

为了符号上的简洁，我们定义 条件KL散度 为两个条件概率分布的KL散度的期望：

\[D_{\mathbb{KL}}(p(y \mid x) \| q(y \mid x)) \triangleq \int d x p(x) \int d y p(y \mid x) \log \frac{p(y \mid x)}{q(y \mid x)} \tag{5.21}\]

5.1.3 关于KL散度的思考

在本节，我们讨论KL散度的一些定性性质。

5.1.3.1 KL的单位

由于KL散度是对数形式的，而不同底数的对数之间只相差一个乘法常数，因此我们在计算KL散度时可以选择对数的底数，就类似于选择测量信息时使用的单位。

如果使用底数为2的对数，则KL的单位为 bits，全称为 “binary digits”。如果使用自然对数，单位为 nats，即 “natural units”。

两种单位的切换很简单，使用 $\log _2 y=\frac{\log y}{\log 2}$。所以

\[\begin{align} & 1 \text { bit }={\ln (2)} \text { nats } \approx 0.693 \text { nats }\tag{5.22} \\ & 1 \text { nat }=\frac{1}{\ln (2)} \text { bits } \approx 1.44 \text { bits } \tag{5.23} \end{align}\]

5.1.3.2 KL散度的非对称性

KL 散度在两个分布之间并不是对称的。虽然许多人在初次接触时会觉得这种不对称令人困惑，但我们可以看到，这种不对称源于我们在5.1.2.5节介绍的自然链式法则。当我们将分布分解为条件分布时，需要在某个分布下求解期望。在 KL 散度中，我们是在第一个分布 $p(x)$ 下计算期望的。这打破了两个分布之间的对称性。

从直观的角度，我们可以看到，从 $q$ 更新到 $p$ 所需的信息通常不同于从 $p$ 更新到 $q$ 所需的信息。例如，考虑两个伯努利分布之间的 KL 散度，第一个分布的成功概率为 0.443，第二个分布的成功概率为 0.975：

\[\mathrm{D}_{\mathbb{KL}}=0.975 \log \frac{0.975}{0.443}+0.025 \log \frac{0.025}{0.557}=0.692 \text { nats } \sim 1.0 \text { bits. } \tag{5.24}\]

所以从分布 $[0.443,0.557]$ 更新到伯努利分布 $[0.975, 0.025]$ 消耗 $1$ bit 的信息。那反过来会是什么情况呢？

\[\mathrm{D}_{\mathbb{KL}}=0.443 \log \frac{0.443}{0.975}+0.557 \log \frac{0.557}{0.025}=1.38 \text { nats } \sim 2.0 \text { bits, } \tag{5.25}\]

因此，反向更新所需的信息量是两个比特，或者说是两倍的信息量。因此，我们可以看到，从一个几乎均匀的分布更新到一个几乎确定的分布大约需要 1 比特的信息，或者说需要一个设计得当的“是/否”问题。而要从接近确定的分布更新到类似于抛硬币的随机分布，需要更多的说服力（信息）。

5.1.3.3 KL as expected weight of evidence

假设我们需要在两个候选分布 $P$ 和 $Q$ 之间进行选择。你收集了一些数据 $D$。贝叶斯定理告诉我们如何更新某个假设的正确性：

\[\operatorname{Pr}(P \mid D)=\frac{\operatorname{Pr}(D \mid P)}{\operatorname{Pr}(D)} \operatorname{Pr}(P) . \tag{5.26}\]

正常情况下，我们需要计算边际似然 $\text{Pr}(D)$，这一点很困难。如果我们考虑两个假设的后验分布的比率：

\[\frac{\operatorname{Pr}(P \mid D)}{\operatorname{Pr}(Q \mid D)}=\frac{\operatorname{Pr}(D \mid P)}{\operatorname{Pr}(D \mid Q)} \frac{\operatorname{Pr}(P)}{\operatorname{Pr}(Q)}, \tag{5.27}\]

此时的边际似然可以被绕开。对上式两边取对数：

\[\log \frac{\operatorname{Pr}(P \mid D)}{\operatorname{Pr}(Q \mid D)}=\log \frac{p(D)}{q(D)}+\log \frac{\operatorname{Pr}(P)}{\operatorname{Pr}(Q)} \tag{5.28}\]

某个假设相较于另一个假设的对数后验概率比等于对数先验分布比加上 **weight of evidence **[Goo85]⁶ ：

\[w[P / Q ; D] \triangleq \log \frac{p(D)}{q(D)} \tag{5.29}\]

基于这个解释，KL 散度实际上是假设 $P$ 相较于假设 $Q$ 的 weight of evidence 的期望值，该期望值在假设分布 $P$ 下进行计算（假设 $P$ 是正确的）。由于KL散度始终为非负值，当我们采样更多数据时，它通常会帮助我们更加支持正确的假设，而不是反对它。实际上，可以将 weight of evidence 解释为 KL 的一种简化版，它们都衡量了两个假设在同一组 evidence （即采样到的数据）上的表现能力。

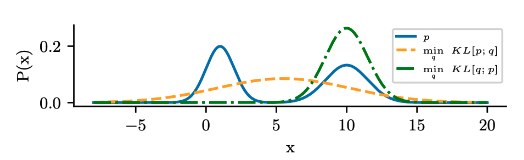
图 $5.1$：mode-covering 或 mode-seeking 的示意图。真实的分布 $p$（蓝色）是双峰的。如果我们是最小化 $D_{\mathbb{KL}}(p | q)$ ，此时的 $q$ （橘色）将覆盖 $p$ 的峰值。当我们最小化 $D_{\mathbb{KL}}(q | p)$ ，此时的 $q$（绿色）将忽略掉 $p$ 的某些峰值。

5.1.4 最小化KL

本节，我们将讨论最小化 $D_{\mathbb{KL}}(p | q)$ 或 $D_{\mathbb{KL}}(q | p)$ 的问题，其中我们假定正确的分布为 $p$，需要优化的分布是 $q$。

5.1.4.1 前向vs逆向KL

KL 的非对称性说明最小化 $D_{\mathbb{KL}}(p | q)$ （又被称为 inclusive KL 或 forward KL）得到的分布 $q$ 与最小化 $D_{\mathbb{KL}}(q | p)$ （又被称为 exclusive KL 或 reverse KL）得到的结果是不同的。举个例子，考虑图5.1中的蓝色双峰分布 $p$ ，我们需要使用一个单峰高斯分布 $q$ 去逼近。

为了避免 $D_{\mathbb{KL}}(p | q)$ 变得无穷大，我们需要确保 $p\gt0$ 的同时 $q\gt 0$ （换句话说， $q$ 必须覆盖所有的 $p$ 的支撑集），所以 $q$ 倾向于覆盖 $p$ 的所有峰值，即所谓的 mode-covering 或者zero-avoiding 行为（橘色曲线）。相反，为了避免 $D_{\mathbb{KL}}(q | p)$ 变得无穷大，我们必须确保 $p=0$ 的同时 $q=0$，即所谓的 mode-seeking 或 zero-forcing 行为（绿色曲线）。

两种优化目标的可视化结果可以参考 https://twitter.com/ari_seff/status/1303741288911638530。

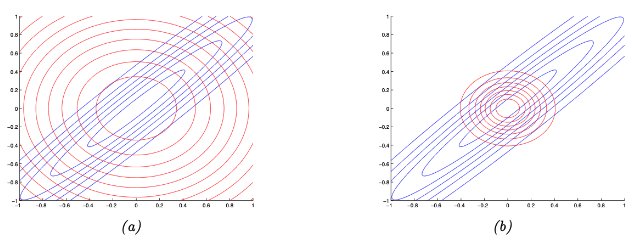
图 $5.2$：在对称高斯分布上说明正向KL与反向KL。蓝色曲线表示真实的分布 $p$。红色曲线表示近似分布 $q$。（a）最小化 $D_{\mathbb{KL}}(p | q)$。（b）最小化 $D_{\mathbb{KL }}(q | p)$。

5.1.4.2 Moment projection (mode covering)

考虑通过最小化 forwards KL 计算分布 $q$:

\[q=\underset{q}{\operatorname{argmin}} D_{\mathbb{KL}}(p \| q) \tag{5.30}\]

这被称为 M-projection 或者 moment projection，因为正如我们接下来要证明的，最优的 $q$ 将与真实的 $p$ 的矩相匹配。 所以优化 $q$ 的过程又被称为 moment matching。

为了说明为什么最优的 $q$ 必须与 $p$ 的矩匹配，不妨假设分布 $q$ 是一个指数族分布：

\[q(\boldsymbol{x})=h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-\log Z(\boldsymbol{\eta})\right] \tag{5.31}\]

其中 $\mathcal{T}(\boldsymbol{x})$ 被称为充分统计量向量， $\boldsymbol{\eta}$ 被称为自然参数。一阶最优解为：

\[\begin{align} \partial_{\eta_i} D_{\mathbb{KL}}(p \| q) & =-\partial_{\eta_i} \int_{\boldsymbol{x}} p(\boldsymbol{x}) \log q(\boldsymbol{x}) \tag{5.32}\\ & =-\partial_{\eta_i} \int_{\boldsymbol{x}} p(\boldsymbol{x}) \log \left(h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-\log Z(\boldsymbol{\eta})\right]\right) \tag{5.33}\\ & =-\partial_{\eta_i} \int_{\boldsymbol{x}} p(\boldsymbol{x})\left(\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-\log Z(\boldsymbol{\eta})\right) \tag{5.34}\\ & =-\int_x p(\boldsymbol{x}) \mathcal{T}_i(\boldsymbol{x})+\mathbb{E}_{q(\boldsymbol{x})}\left[\mathcal{T}_i(\boldsymbol{x})\right] \tag{5.35}\\ & =-\mathbb{E}_{p(\boldsymbol{x})}\left[\mathcal{T}_i(\boldsymbol{x})\right]+\mathbb{E}_{q(\boldsymbol{x})}\left[\mathcal{T}_i(\boldsymbol{x})\right]=0 \tag{5.36} \end{align}\]

上式倒数第二行利用了对数配分函数的导数等于充分统计量的期望值（参考公式 2.216）。所以两个分布的充分统计量的期望值（即分布的矩）必须匹配。

举个例子，假设真实的目标分布 $p$ 是一个具有完全协方差矩阵的 $2d$ 高斯分布，$p(\boldsymbol{x})=\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Lambda}^{-1}\right)$，其中

\[\boldsymbol{\mu}=\binom{\mu_1}{\mu_2}, \quad \boldsymbol{\Sigma}=\left(\begin{array}{ll} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{12}^{\top} & \Sigma_{22} \end{array}\right) \quad \mathbf{\Lambda}=\left(\begin{array}{ll} \Lambda_{11} & \Lambda_{12} \\ \Lambda_{12}^{\top} & \Lambda_{22} \end{array}\right) \tag{5.37}\]

我们使用2个1d对角高斯分布的乘积 $q$ 来近似分布 $p$：

\[q(\boldsymbol{x} \mid \boldsymbol{m}, \mathbf{V})=\mathcal{N}\left(x_1 \mid m_1, v_1\right) \mathcal{N}\left(x_2 \mid m_2, v_2\right) \tag{5.38}\]

如果我们使用矩匹配，最优的 $q$ 必然满足如下的形式：

\[q(\boldsymbol{x})=\mathcal{N}\left(x_1 \mid \mu_1, \Sigma_{11}\right) \mathcal{N}\left(x_2 \mid \mu_2, \Sigma_{22}\right) \tag{5.39}\]

在图5.2(a) 中，我们展示了最终的分布。我们发现 $q$ 覆盖（包含）$p$，但它的支撑集覆盖面更广（相应的，每个点的概率值偏低，即under-confidence）。

5.1.4.3 Information projection (mode seeking)

现在通过最小化 reverse KL 优化 $q$:

\[q=\underset{q}{\operatorname{argmin}} D_{\mathbb{KL}}(q \| p) \tag{5.40}\]

这被称为 I-projection 或者 information projection。该优化问题通常更加简单，因为优化目标需要关于分布 $q$ 计算期望，所以我们可以选择那些容易处理的分布族。

作为一个例子，同样假设真实分布是一个具有完全协方差矩阵的高斯分布，$p(\boldsymbol{x})=\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Lambda}^{-1}\right)$，同时令近似的分布是一个具有对角协方差矩阵的高斯分布 $q(\boldsymbol{x})=\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{m}, \operatorname{diag}(\boldsymbol{v}))$。可以证明（参考附录 5.1.2 节）最优的变分参数满足 $\boldsymbol{m}=\boldsymbol{\mu}$ 和 $v_i=\boldsymbol{\Lambda}_{i i}^{-1}$。图5.2(b) 给出了说明。我们发现近似的分布方差特别狭窄，换句话说，近似的分布是over-confident 的。然而需要注意的是，最小化 reverse KL 并不总是导致一个过于紧凑的近似分布，相关解释参考 [Tur+08]⁷。

5.1.5 KL的属性

接下来我们将介绍一些KL散度的有用的属性。

5.1.5.1 压缩引理

KL散度的一个重要属性是压缩引理（compression lemma）：

定理5.1.2. 对任意具有良好KL定义的分布 $P$ 和 $Q$，任意与分布处于同一定义域的标量函数 $\phi$ 满足：

\[\mathbb{E}_P[\phi] \leq \log \mathbb{E}_Q\left[e^\phi\right]+D_{\mathbb{KL}}(P \| Q) \tag{5.41}\]

证明. 已知任意两个分布之间的 KL 散度总是非负的。考虑如下形式的分布：

\[g(x)=\frac{q(x)}{\mathcal{Z}} e^{\phi(x)} \tag{5.42}\]

其中 配分函数 定义为：

\[\mathcal{Z}=\int d x q(x) e^{\phi(x)} \tag{5.43}\]

计算分布 $p(x)$ 和 $g(x)$ 之间的 KL 散度，我们有：

\[D_{\mathbb{KL}}(P \| G)=D_{\mathbb{KL}}(P \| Q)-\mathbb{E}_P[\phi(x)]+\log (\mathcal{Z}) \geq 0. \tag{5.44}\]

compression lemma实际上提供了KL散度的Donsker-Varadhan变分表示：

\[D_{\mathbb{KL}}(P \| Q)=\sup _\phi \mathbb{E}_P[\phi(x)]-\log \mathbb{E}_Q\left[e^{\phi(x)}\right] . \tag{5.45}\]

对所有定义域与分布相同的函数 $\phi$，KL散度是式（5.45）右侧能取到的最大值。对于任意固定的函数 $\phi(x)$，上式右侧提供了一个关于KL散度的下确界。

压缩引理的另一个用途是，它提供了一种估计某些函数在未知分布 $P$ 下的期望的方法。基于这种思想，压缩引理可以用来推导一组PAC-Bayes确界的结果，这些确界将损失函数（如上式的 $\phi$）相对于真实分布（如分布 $P$）的表现与在有限训练集（如分布 $Q$）上测量的损失联系起来。例如，参考第17.4.5节或Banerjee [Ban06]⁸。

5.1.5.2 KL的数据处理不等式

对于来自两个不同分布的样本，任何对样本进行的后处理都会使两个分布彼此更加接近。这被称为数据处理不等式（data processing inequality），因为它表明，通过对数据进行处理，并不能增加从 $q$ 到 $p$ 的信息增益。

定理5.1.3. 考虑两个不同的分布 $p(x)$ 和 $q(x)$，以及一个概率信道 $t(y∣x)$。如果 $p(y)$ 是 $p(x)$ 经过信道 $t(y∣x)$ 后得到的分布，同理 $q(y)$ 也是 $q(x)$ 经过信道处理后得到的分布，则我们有：

\[D_{\mathbb{KL}}(p(x) \| q(x)) \geq D_{\mathbb{KL}}(p(y) \| q(y)) \tag{5.46}\]

证明. 证明过程再次使用了 5.1.2.2 节的琴森不等式。考虑到 $p(x, y)=p(x) t(y \mid x)$ 和 $q(x, y)=q(x) t(y \mid x)$。

\[\begin{align} D_{\mathbb{KL}}(p(x) \| q(x)) & =\int d x p(x) \log \frac{p(x)}{q(x)} \tag{5.47} \\ & =\int d x \int d y p(x) t(y \mid x) \log \frac{p(x) t(y \mid x)}{q(x) t(y \mid x)} \tag{5.48}\\ & =\int d x \int d y p(x, y) \log \frac{p(x, y)}{q(x, y)} \tag{5.49}\\ & =-\int d y p(y) \int d x p(x \mid y) \log \frac{q(x, y)}{p(x, y)} \tag{5.50}\\ & \geq-\int d y p(y) \log \left(\int d x p(x \mid y) \frac{q(x, y)}{p(x, y)}\right) \tag{5.51}\\ & =-\int d y p(y) \log \left(\frac{q(y)}{p(y)} \int d x q(x \mid y)\right) \tag{5.52}\\ & =\int d y p(y) \log \frac{p(y)}{q(y)}=D_{\mathbb{KL}}(p(y) \| q(y)) \tag{5.53} \end{align}\]

上述结果的一种解释是，任何对随机样本的处理都会使两个分布变得难以区分。

作为一种特殊的数据处理方式式，我们可以仅对部分随机变量进行边缘化。

推论 5.1.1. （KL散度的单调性）

\[D_{\mathbb{KL}}(p(x, y) \| q(x, y)) \geq D_{\mathbb{KL}}(p(x) \| q(x)) \tag{5.54}\]

证明. 证明过程跟上面一样。

\[\begin{align} D_{\mathbb{KL}}(p(x, y) \| q(x, y)) & =\int d x \int d y p(x, y) \log \frac{p(x, y)}{q(x, y)} \tag{5.55}\\ & =-\int d y p(y) \int d x p(x \mid y) \log \left(\frac{q(y)}{p(y)} \frac{q(x \mid y)}{p(x \mid y)}\right) \tag{5.56}\\ & \geq-\int d y p(y) \log \left(\frac{q(y)}{p(y)} \int d x q(x \mid y)\right) \tag{5.57}\\ & =\int d y p(y) \log \frac{p(y)}{q(y)}=D_{\mathbb{KL}}(p(y) \| q(y)) \tag{5.58} \end{align}\]

对该结果的一种直观解释是，相较于观测到全部随机变量，只观测到部分随机变量，会增加区分两个分布的难度。

5.1.6 KL散度和MLE

假设我们想找到与分布 $p$ 在 KL 散度维度最近的分布 $q$：

\[q^*=\arg \min _q D_{\mathbb{KL}}(p \| q)=\arg \min _q \int p(x) \log p(x) d x-\int p(x) \log q(x) d x \tag{5.60}\]

假设 $p$ 是一个经验分布，该分布将全部概率质量分配到观测数据：

\[p_{\mathcal{D}}(x)=\frac{1}{N} \sum_{n=1}^N \delta\left(x-x_n\right) \tag{5.61}\]

使用 delta 函数的平移属性，我们有

\[\begin{align} D_{\mathbb{KL}}\left(p_{\mathcal{D}} \| q\right) & =-\int p_{\mathcal{D}}(x) \log q(x) d x+C \tag{5.62}\\ & =-\int\left[\frac{1}{N} \sum_n \delta\left(x-x_n\right)\right] \log q(x) d x+C \tag{5.63} \\ & =-\frac{1}{N} \sum_n \log q\left(x_n\right)+C \tag{5.64} \end{align}\]

其中 $C=\int p_{\mathcal{D}}(x) \log p_{\mathcal{D}}(x)$ 是与 $q$ 无关的常量。

我们可以将上式重写成

\[D_{\mathbb{KL}}\left(p_{\mathcal{D}} \| q\right)=\mathbb{H}_{c e}\left(p_{\mathcal{D}}, q\right)-\mathbb{H}\left(p_{\mathcal{D}}\right) \tag{5.65}\]

其中

\[\mathbb{H}_{c e}(p, q) \triangleq-\sum_k p_k \log q_k \tag{5.66}\]

被称为 交叉熵（cross entropy）。\(\mathbb{H}_{c e}\left(p_{\mathcal{D}}, q\right)\) 是分布 $q$ 在训练集上的平均负对数似然。所以，最小化与经验分布之间的KL散度等价于最大似然。

这一视角指出了基于似然的训练方法的缺陷，即它过分依赖于训练集本身。在大多数应用中，我们并不认为经验分布是对真实分布的良好近似，因为它只是将“尖峰”集中在有限的几个数据点上，而在其他地方的密度为零。即使数据集非常大（比如 100 万张图片），从中采样的数据的“宇宙”通常更大（例如，“所有自然图像”的集合远大于 100 万）。因此，我们需要以某种方式通过在“相似”的输入之间共享概率质量来平滑经验分布。

5.1.7 KL散度和贝叶斯推断（这段比较难理解）

贝叶斯推断本身可以看作一个通过最小化KL散度得到的特定解。

考虑先验分布的形式为一个联合概率分布 $q(\theta, D)=q(\theta) q(D \mid \theta)$，包含某个先验 $q(\theta)$ 和某个似然 $q(D \mid \theta)$。如果我们刚好观察到某些特定的数据集 $D_0$，我们如何更新我们的信念呢？我们需要搜索尽可能接近已有信念的联合分布，但要同时满足已有数据的约束：

\[p(\theta, D)=\operatorname{argmin} D_{\mathbb{KL}}(p(\theta, D) \| q(\theta, D)) \text { such that } p(D)=\delta\left(D-D_0\right) . \tag{5.67}\]

其中 $\delta\left(D-D_0\right)$ 是一个退化分布，它将所有的概率质量集中在与$D_0$完全相同的数据集 $D$ 上。将 KL 散度展开为链式法则形式：

\[D_{\mathbb{KL}}(p(\theta, D) \| q(\theta, D))=D_{\mathbb{KL}}(p(D) \| q(D))+D_{\mathbb{KL}}(p(\theta \mid D) \| q(\theta \mid D)) \tag{5.68}\]

显然，最优解为：

\[p(\theta, D)=p(D) p(\theta \mid D)=\delta\left(D-D_0\right) q(\theta \mid D) \tag{5.69}\]

更新后的边际分布为：

\[p(\theta)=\int d D p(\theta, D)=\int d D \delta\left(D-D_0\right) q(\theta \mid D)=q\left(\theta \mid D=D_0\right), \tag{5.70}\]

这只是我们基于我们观察到的数据，从先验信念中得到的一般形式的贝叶斯后验。

相比之下，贝叶斯定理的通常表述只是对概率链式法则的一个简单利用：

\[q(\theta, D)=q(D) q(\theta \mid D)=q(\theta) q(D \mid \theta) \Longrightarrow q(\theta \mid D)=\frac{q(D \mid \theta)}{q(D)} q(\theta) . \tag{5.71}\]

注意到，上式将条件分布 $q(\theta \mid D)$与$q(D \mid \theta)$ 、$q(\theta)$ 和 $q(D)$ 进行了关联，但这些都是表示同一分布的不同方式。贝叶斯定理并没有告诉我们在得到证据后应如何更新我们的信念，对于这一点，我们需要其他的方法 [Cat+11]⁹。

这段关于贝叶斯推理的解释有一个优点，那就是它自然地可以推广到其他形式的约束，而不是假设我们已经完全观测到数据。

如果存在一些额外的测量误差，并且这些误差是我们充分理解的，那么我们应该做的不是将更新后的信念限定为一个狄拉克δ函数——只针对观测到的数据，而是将其固定为我们理解的分布 $p(D)$。例如，我们可能不知道数据的确切值，但在测量后，我们认为它是一个具有某个均值和标准差的高斯分布。

由于KL散度的链式法则，这对我们更新后的条件分布没有影响，条件分布仍然是贝叶斯后验：$p(\theta \mid D)=q(\theta \mid D)$。然而，这会改变我们对参数的边际信念，这些边际信念现在是：

\[p(\theta)=\int d D p(D) q(\theta \mid D) \tag{5.72}\]

贝叶斯法则的这个推广有时被称为杰弗瑞条件化规则（Jeffrey’s conditionalization rule）[Cat08]¹⁰。

5.1.8 KL散度和指数族

对于同属指数族中的两个同类分布，它们之间的KL散度具有很好的闭合形式，如下所述。

考虑 $p(\boldsymbol{x})$ 的自然参数 $\boldsymbol{\eta}$， base measure $h(\boldsymbol{x})$ 和充分统计量 $\mathcal{T}(\boldsymbol{x})$：

\[p(\boldsymbol{x})=h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-A(\boldsymbol{\eta})\right] \tag{5.73}\]

其中

\[A(\boldsymbol{\eta})=\log \int h(\boldsymbol{x}) \exp \left(\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})\right) d \boldsymbol{x} \tag{5.74}\]

表示对数配分函数，它是关于 $\boldsymbol{\eta}$ 的凸函数。

两个同属指数族的同类分布之间的KL散度为：

\[\begin{align} D_{\mathrm{KL}}\left(p\left(\boldsymbol{x} \mid \boldsymbol{\eta}_1\right) \| p\left(\boldsymbol{x} \mid \boldsymbol{\eta}_2\right)\right) & =\mathbb{E}_{\boldsymbol{\eta}_1}\left[\left(\boldsymbol{\eta}_1-\boldsymbol{\eta}_2\right)^{\mathrm{T}} \mathcal{T}(\boldsymbol{x})-A\left(\boldsymbol{\eta}_1\right)+A\left(\boldsymbol{\eta}_2\right)\right] \tag{5.75}\\ & =\left(\boldsymbol{\eta}_1-\boldsymbol{\eta}_2\right)^{\top} \boldsymbol{\mu}_1-A\left(\boldsymbol{\eta}_1\right)+A\left(\boldsymbol{\eta}_2\right) \tag{5.76} \end{align}\]

其中 \(\boldsymbol{\mu}_j \triangleq \mathbb{E}_{\boldsymbol{\eta}_j}[\mathcal{T}(\boldsymbol{x})]\)。

5.1.8.1 案例：高斯分布之间的KL散度

两个多变量高斯分布的KL散度为：

\[\begin{align} & D_{\mathbb{KL}}\left(\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1\right) \| \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2\right)\right) \\ & =\frac{1}{2}\left[\operatorname{tr}\left(\boldsymbol{\Sigma}_2^{-1} \boldsymbol{\Sigma}_1\right)+\left(\boldsymbol{\mu}_2-\boldsymbol{\mu}_1\right)^{\top} \boldsymbol{\Sigma}_2^{-1}\left(\boldsymbol{\mu}_2-\boldsymbol{\mu}_1\right)-D+\log \left(\frac{\operatorname{det}\left(\boldsymbol{\Sigma}_2\right)}{\operatorname{det}\left(\boldsymbol{\Sigma}_1\right)}\right)\right] \end{align} \tag{5.77}\]

在标量的情况下：

\[D_{\mathbb{KL}}\left(\mathcal{N}\left(x \mid \mu_1, \sigma_1\right) \| \mathcal{N}\left(x \mid \mu_2, \sigma_2\right)\right)=\log \frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+\left(\mu_1-\mu_2\right)^2}{2 \sigma_2^2}-\frac{1}{2} \tag{5.78}\]

5.1.9 使用 Fisher 信息矩阵近似KL散度

令 $p_\boldsymbol{\theta}(\boldsymbol{x})$ 和 $p_\boldsymbol{\theta’}(\boldsymbol{x})$ 表示两个分布，其中 $\boldsymbol{\theta}’=\boldsymbol{\theta}+\boldsymbol{\delta}$ 。我们可以评估两个分布之间的距离，通过它们的预测分布（而不是在参数空间对比分布）：

\[D_{\mathbb{KL}}\left(p_{\boldsymbol{\theta}} \| p_{\boldsymbol{\theta}^{\prime}}\right)=\mathbb{E}_{p_{\boldsymbol{\theta}}(\boldsymbol{x})}\left[\log p_{\boldsymbol{\theta}}(\boldsymbol{x})-\log p_{\boldsymbol{\theta}^{\prime}}(\boldsymbol{x})\right] \tag{5.79}\]

使用二阶泰勒展开对上式进行近似：

\[D_{\mathbb{KL}}\left(p_{\boldsymbol{\theta}} \| p_{\boldsymbol{\theta}^{\prime}}\right) \approx-\boldsymbol{\delta}^{\top} \mathbb{E}\left[\nabla \log p_{\boldsymbol{\theta}}(\boldsymbol{x})\right]-\frac{1}{2} \boldsymbol{\delta}^{\top} \mathbb{E}\left[\nabla^2 \log p_{\boldsymbol{\theta}}(\boldsymbol{x})\right] \boldsymbol{\delta} \tag{5.80}\]

考虑到 score function 的期望值为 0（根据式 (3.44)），我们有：

\[D_{\mathbb{KL}}\left(p_{\boldsymbol{\theta}} \| p_{\boldsymbol{\theta}^{\prime}}\right) \approx \frac{1}{2} \boldsymbol{\delta}^{\top} \mathbf{F}(\boldsymbol{\theta}) \boldsymbol{\delta} \tag{5.81}\]

其中 $\mathbf{F}$ 表示费舍尔信息矩阵

\[\mathbf{F}=-\mathbb{E}\left[\nabla^2 \log p_{\boldsymbol{\theta}}(\boldsymbol{x})\right]=\mathbb{E}\left[\left(\nabla \log p_{\boldsymbol{\theta}}(\boldsymbol{x})\right)\left(\nabla \log p_{\boldsymbol{\theta}}(\boldsymbol{x})\right)^{\top}\right] \tag{5.82}\]

因此，KL 散度大致等于使用 Fisher 信息矩阵作为度量的（平方）马氏距离。这个结论是第 6.4 节中讨论的自然梯度（natural gradient）方法的基础。

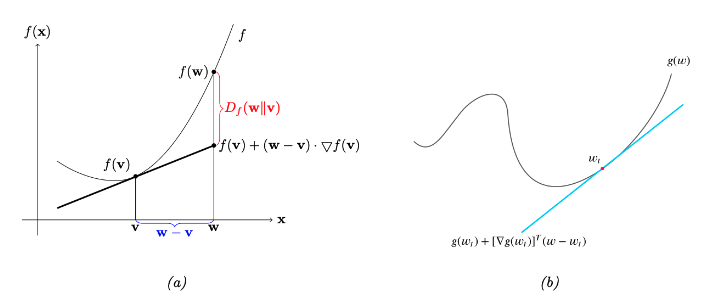
图 $5.3$：（a）Bregman 散度的示意图。（b）非凸函数的局部线性近似。

5.1.10 Bregman散度

令 $f:\Omega\rightarrow \mathbb{R}$ 表示一个连续可微的严格凸函数，定义域是一个封闭的凸集 $\Omega$。我们定义关于函数 $f$ 的Bregman散度[Bre67]¹¹：

\[B_f(\boldsymbol{w} \| \boldsymbol{v})=f(\boldsymbol{w})-f(\boldsymbol{v})-(\boldsymbol{w}-\boldsymbol{v})^{\top} \nabla f(\boldsymbol{v}) \tag{5.83}\]

为了理解这一点，令

\[\hat{f}_\boldsymbol{v}(\boldsymbol{w})=f(\boldsymbol{v})+(\boldsymbol{w}-\boldsymbol{v})^{\mathrm{T}} \nabla f(\boldsymbol{v}) \tag{5.84}\]

表示 $f$ 在 $\boldsymbol{v}$ 处的一阶泰勒展开近似。Bregman散度是线性近似的偏差：

\[B_f(\boldsymbol{w} \| \boldsymbol{v})=f(\boldsymbol{w})-\hat{f}_{\boldsymbol{v}}(\boldsymbol{w})\tag{5.85}\]

图5.3a 给出了说明。考虑到 $f$ 是凸函数，我们有 $B_f(\boldsymbol{w} | \boldsymbol{v}) \geq 0$，因为 $\hat{f}_\boldsymbol{v}$ 是函数 $f$ 的一个线性下确界。

接下来，我们将介绍一些Bregman散度的重要特例。

• 如果 $f(\boldsymbol{w})=|\boldsymbol{w}|^2$，那么 $B_f(\boldsymbol{w} | \boldsymbol{v})=|\boldsymbol{w}-\boldsymbol{v}|^2$ 表示平方欧式距离。
• 如果 $f(\boldsymbol{w})=\boldsymbol{w}^{\top} \mathbf{Q} \boldsymbol{w}$，那么 $B_f(\boldsymbol{w} | \boldsymbol{v})$ 表示平方马氏距离。
• 如果 $\boldsymbol{w}$ 是指数族分布的自然参数，则 $f(\boldsymbol{w})=\log Z(\boldsymbol{w})$ 表示log normalizer，此时 Bregman散度与 KL 散度相同，如5.1.10.1 节所述。

5.1.10.1 KL 散度是一个 Bregman 散度

考虑到对数配分函数 $A(\boldsymbol{\eta})$ 是一个凸函数。所以我们可以用它定义 Bregman 散度（参见 5.1.10节）：

\[\begin{align} B_f\left(\boldsymbol{\eta}_q \| \boldsymbol{\eta}_p\right) & =A\left(\boldsymbol{\eta}_q\right)-A\left(\boldsymbol{\eta}_p\right)-\left(\boldsymbol{\eta}_q-\boldsymbol{\eta}_p\right)^{\top} \nabla_{\boldsymbol{\eta}_p} A\left(\boldsymbol{\eta}_p\right) \tag{5.86}\\ & =A\left(\boldsymbol{\eta}_q\right)-A\left(\boldsymbol{\eta}_p\right)-\left(\boldsymbol{\eta}_q-\boldsymbol{\eta}_p\right)^{\top} \mathbb{E}_p[\mathcal{T}(\boldsymbol{x})] \tag{5.87}\\ & =D_{\mathbb{KL}}(p \| q) \tag{5.88} \end{align}\]

其中我们利用了对数配分函数的梯度等于充分统计量的期望。

事实上，KL 散度是唯一一种既是Bregman散度又是$f-$散度的散度[Ama09]¹²。

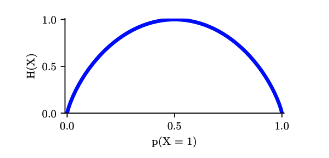
图 $5.4$：伯努利随机变量的熵作为$\theta$的函数。最大熵为 $\log _2 2=1$。

5.2 熵（Entropy）

本节，我们将讨论一个分布的熵（entropy），我们将会发现，它实际上是概率分布与均匀分布之间的KL散度的一个平移缩放版本。

5.2.1 定义

首先考虑一个包含 $K$ 个状态的离散随机变量 $X$，服从分布 $p$，它的熵定义为

\[\mathbb{H}(X) \triangleq-\sum_{k=1}^K p(X=k) \log p(X=k)=-\mathbb{E}_X[\log p(X)] \tag{5.89}\]

我们可以使用任意基底的对数函数，但通常使用 2 或者 e，前者对应单位 bits，后者对应单位 nats。正如我们在 5.1.3.1 节中解释的那样。

实际上，上述的熵等价于一个常数减去该分布与均匀分布之间的KL散度：

\[\begin{align} \mathbb{H}(X) & =\log K-D_{\mathbb{KL}}(p(X) \| u(X)) \tag{5.90}\\ D_{\mathbb{KL}}(p(X) \| u(X)) & =\sum_{k=1}^K p(X=k) \log \frac{p(X=k)}{\frac{1}{K}} \tag{5.91} \\ & =\log K+\sum_{k=1}^K p(X=k) \log p(X=k) \tag{5.92} \end{align}\]

如果 $p$ 是均匀分布，那 KL 散度等于0，此时的熵达到最大值 $\log K$。

对于特殊的二元随机变量，$X \in{0,1}$，我们可以令 $p(X=1)=\theta$ 和 $p(X=0)=1-\theta$。所以此时的熵等于

\[\begin{align} \mathbb{H}(X) & =-[p(X=1) \log p(X=1)+p(X=0) \log p(X=0)] \tag{5.93} \\ & =-[\theta \log \theta+(1-\theta) \log (1-\theta)] \tag{5.94} \end{align}\]

这被称为 二元熵函数（binary entropy function），也可以写成 $\mathbb{H}(\theta)$。我们可以绘制如 5.4 的图。不难发现，最大值出现在 $\theta=0.5$ 处，此时对应的最大值为 1 bit——一枚均质的硬币需要一个是/否的问题来确定其状态。

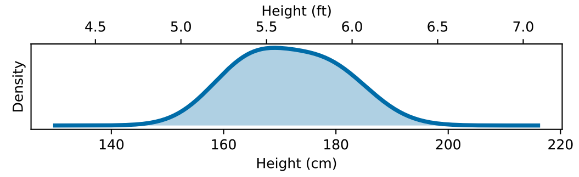
图 $5.5$：成人身高的分布。该分布的连续熵取决于其测量单位。如果身高以英尺为单位测量，则该分布的连续熵为0.43比特；如果以厘米为单位测量，则为5.4比特；如果以米为单位测量，则为-1.3比特。数据来源：https://ourworldindata.org/human-height。

5.2.2 连续随机变量的可微熵

如果 $X$ 是一个连续随机变量，且概率密度函数为 $p(x)$，我们定义 可微熵（differential entropy） 为 \(h(X) \triangleq-\int_X d x p(x) \log p(x) \tag{5.95}\) 其中我们假设上述积分存在。

比方说，$d$ 维高斯分布的熵为：

\[h(\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma}))=\frac{1}{2} \log |2 \pi e \boldsymbol{\Sigma}|=\frac{1}{2} \log \left[(2 \pi e)^d|\boldsymbol{\Sigma}|\right]=\frac{d}{2}+\frac{d}{2} \log (2 \pi)+\frac{1}{2} \log |\boldsymbol{\Sigma}|\tag{5.96}\]

在 1d 情况下：

\[h\left(\mathcal{N}\left(\mu, \sigma^2\right)\right)=\frac{1}{2} \log \left[2 \pi e \sigma^2\right] \tag{5.97}\]

需要注意的是，与离散情况不同，可微熵有可能是负的。这是因为概率密度函数可能大于1。比方说，假设 $X \sim U(0, a)$。此时

\[h(X)=-\int_0^a d x \frac{1}{a} \log \frac{1}{a}=\log a \tag{5.98}\]

如果我们令 $a=\frac{1}{8}$，我们有 $h(X)=\log _2(1 / 8)=-3$ bits.

理解可微熵的一种方式是意识到所有实数只能以有限精度表示。可以证明[CT91，第228页][^CT91]，连续随机变量$X$的$n$位量化的熵大约是$h(X) + n$。例如，假设 $X \sim U\left(0, \frac{1}{8}\right)$。那么，在 $X$ 的二进制表示中，小数点右侧的前三位必须为$0$（因为该数小于或等于$1/8$）。因此，要以 $n$ 位精度描述 $X$，只需要 $n - 3$ 位，这与上述计算的 $h(X) = -3$ 一致。

可微熵也缺乏KL散度的重参数不变的属性（参见第5.1.2.3节）。具体而言，如果我们对随机变量进行变换 $y=f(x)$，则熵也会发生变化。要理解这一点，注意到随机变量的变换满足：

\[p(y) d y=p(x) d x \Longrightarrow p(y)=p(x)\left|\frac{d y}{d x}\right|^{-1} \tag{5.99}\]

所以连续熵的变换满足：

\[h(X)=-\int d x p(x) \log p(x)=h(Y)-\int d y p(y) \log \left|\frac{d y}{d x}\right| . \tag{5.100}\]

在连续熵中，会引入一个额外的因子，即变换雅可比行列式的对数。这即使是在简单的重新缩放随机变量时（例如改变单位时）也会改变连续熵的值。例如，在图5.5中，我们展示了成人身高的分布（它是双峰的，因为男性和女性的身高都服从正态分布，但差异显著）。这个连续熵依赖于其测量单位。如果用英尺为单位，连续熵为0.43比特。直观地讲，这是因为人类身高大多分布在不到一英尺的范围内。如果使用厘米为单位，则连续熵为5.4比特。1英尺等于30.48厘米，而$\log_2{30.48} = 4.9$，这解释了差异的原因（0.43+4.9=5.3）。如果我们用米为单位测量同一分布的连续熵，结果将是-1.3比特！

5.2.3 Typical sets（典型集）

概率分布的典型集是这样一组元素：它们的信息含量接近于从该分布中随机抽样所期望的信息含量。更精确的定义是，对于支撑集为 $\boldsymbol{x} \in \mathcal{X}$ 的分布 $p(\boldsymbol{x})$， 它的 $\epsilon-$典型集 $\mathcal{A}_{\epsilon}^N \in \mathcal{X}^N$ 是所有长度为 $N$ 的序列的集合，同时满足

\[\mathbb{H}(p(\boldsymbol{x}))-\epsilon \leq-\frac{1}{N} \log p\left(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_N\right) \leq \mathbb{H}(p(\boldsymbol{x}))+\epsilon \tag{5.101}\]

如果我们假设 \(p(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_N)=\prod_{n=1}^N p(\boldsymbol{x}_n)\)，那我们可以将中间的项看作熵的 N-sample 经验近似（参考式5.89）。asymptotic equipartition property（AEP）表明该近似在 $N \rightarrow \infty$ 时将依概率收敛到真正的熵[CT06]³。所以典型集发生的概率接近 1，它可以作为分布 $p(\boldsymbol{x})$ 产生的样本的紧凑概括。

5.2.4 交叉熵和不确定性（perplexity）

评估一个模型分布 $q$ 和一个真实分布 $p$ 之间的距离的标准方案是 KL 散度：

\[D_{\mathbb{KL}}(p \| q)=\sum_x p(x) \log \frac{p(x)}{q(x)}=\mathbb{H}_{c e}(p, q)-\mathbb{H}(p) \tag{5.102}\]

其中 $\mathbb{H}_{c e}(p, q)$ 是交叉熵（cross entropy）

\[\mathbb{H}_{c e}(p, q)=-\sum_x p(x) \log q(x) \tag{5.103}\]

$\mathbb{H}(p)=\mathbb{H}_{c e}(p, p)$ 是分布 $p$ 的熵，它是与模型分布 $q$ 无关的常量。

在语言模型中，通常使用另一个替代的性能指标——不确定性（perplexity）。定义为：

\[\operatorname{perplexity}(p, q) \triangleq 2^{\mathbb{H}_{c e}(p, q)} \tag{5.104}\]

我们可以计算交叉熵的经验近似。假设我们使用经验分布近似真实的分布 $p$：

\[P_{\mathcal{D}}(x \mid \mathcal{D})=\frac{1}{N} \sum_{n=1}^N \mathbb{I}\left(x=x_n\right) \tag{5.105}\]

在这种情况下，交叉熵为：

\[H=-\frac{1}{N} \sum_{n=1}^N \log p\left(x_n\right)=-\frac{1}{N} \log \prod_{n=1}^N p\left(x_n\right) \tag{5.106}\]

对应的不确定性为

\[\begin{align} \operatorname{perplexity}\left(p_{\mathcal{D}}, q\right) & =2^{-\frac{1}{N} \log \left(\prod_{n=1}^N p\left(x_n\right)\right)}=2^{\log \left(\prod_{n=1}^N p\left(x_n\right)\right)^{-\frac{1}{N}}} \tag{5.107}\\ & =\left(\prod_{n=1}^N p\left(x_n\right)\right)^{-1 / N}=\sqrt[N]{\prod_{n=1}^N \frac{1}{p\left(x_n\right)}} \tag{5.108} \end{align}\]

在语言模型中，我们通常在预测下一个单词时，以前面的单词作为已知条件。例如，在一个二元语法模型（bigram model）中，我们使用如下形式的二阶马尔可夫模型：\(p(x_n \mid x_{n-1})\)。我们定义语言模型的分支因子（branching factor）为模型预测的下一个可能单词的数量。例如，假设模型以均等的可能预测每个单词，即 \(p(x_n \mid x_{n-1}) = 1/K\)，其中 $K$ 是词汇表中的单词总数。那么，困惑度（perplexity）为：\(((1 / K)^N)^{-1 / N}=K\)。如果某些单词的可能性更高，并且模型能够正确反映这种情况，那么模型的困惑度将低于$K$。然而，考虑到 \(\mathbb{H}(p^*) \leq \mathbb{H}_{c e}(p^*, q)\)，因此我们无法将困惑度降低到 \(2^{-\mathbb{H}\left(p^*\right)}\)以下。

5.3 互信息（Mutual information）

KL 散度衡量了两个分布之间的相似程度。那如何评估两个随机变量之间的相关程度呢？我们可以将评估两个随机变量的相关性的问题转换成衡量它们所服从的分布之间的相似度的问题。基于此，我们定义两个随机变量之间的 互信息（mutual information, MI）。

5.3.1 定义

两个随机变量 $X$ 和 $Y$ 之间的互信息定义为：

\[\mathbb{I}(X ; Y) \triangleq D_{\mathbb{KL}}(p(x, y) \| p(x) p(y))=\sum_{y \in Y} \sum_{x \in X} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} \tag{5.109}\]

（我们使用 $\mathbb{I}(X ; Y)$ 而非 $\mathbb{I}(X, Y)$，如果 $X$ 和 $Y$ 分别是一组随机变量集合。比方说，我们用 $\mathbb{I}(X ; Y,Z)$ 来表示 $X$ 和 $(Y,Z)$ 之间的 MI）。对于连续随机变量，我们只需要将上式中的求和变成积分。

不难发现 MI 始终是非负的，哪怕是对于连续随机变量，因为

\[\mathbb{I}(X ; Y)=D_{\mathbb{KL}}(p(x, y) \| p(x) p(y)) \geq 0 \tag{5.110}\]

当且仅当 $p(x, y)=p(x) p(y)$ 时，上式等于0.

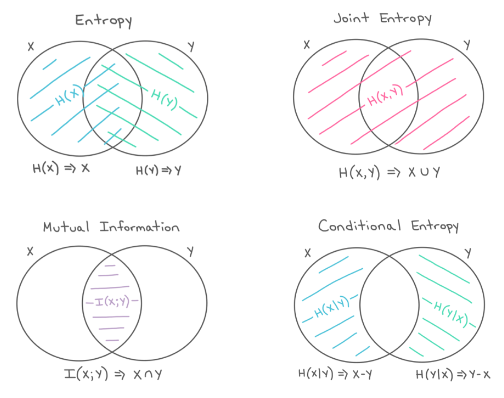
图 $5.6$：边际熵、联合熵、条件熵和互信息以信息图的形式表示。经 Katie Everett 友好授权使用。

5.3.2 解释

考虑到互信息实际上是联合概率分布和分解边际分布之间的 KL散度，说明互信息实际上衡量了将一个模型从 “将两个随机变量看作独立变量”更新到“真实的联合分布”的信息增益。

为了进一步理解 MI，我们将其重新写成联合熵和条件熵的表达式：

\[\mathbb{I}(X ; Y)=\mathbb{H}(X)-\mathbb{H}(X \mid Y)=\mathbb{H}(Y)-\mathbb{H}(Y \mid X) \tag{5.111}\]

所以我们可以将 $X$ 和 $Y$ 之间的MI解释为在观察到 $Y$ 之后，$X$ 的不确定度的下降，或者，对称来看，在观察到 $X$ 之后，$Y$ 的不确定度的下降。顺便说一句，这个结果提供了另一个证明，即额外的条件作用会导致熵减。具体而言，我们有 $0 \leq \mathbb{I}(X ; Y)=\mathbb{H}(X)-\mathbb{H}(X \mid Y)$，所以 $\mathbb{H}(X \mid Y) \leq \mathbb{H}(X)$。

我们也可以从另一个角度进行解释。可以证明

\[\mathbb{I}(X ; Y)=\mathbb{H}(X, Y)-\mathbb{H}(X \mid Y)-\mathbb{H}(Y \mid X) \tag{5.112}\]

最后，我们有

\[\mathbb{I}(X ; Y)=\mathbb{H}(X)+\mathbb{H}(Y)-\mathbb{H}(X, Y) \tag{5.113}\]

参见图5.6，它以信息图（information diagram）的形式总结了这些公式。（严格来说，这是一个有符号测度，将集合表达式映射到它们在信息论领域对应的表达[Yeu91a]¹³。）

5.3.3 数据处理不等式（Data processing inequality）

假设我们有一个未知变量 $X$，以及它的一个含噪的观测版本 $Y$。如果我们以某种方式处理这个含噪观测，并获得一个新的变量 $Z$，显然我们并不能获得更多关于未知变量 $X$ 的信息。这被称为 数据处理不等式（data processing inequality）。接下来我们将正式介绍这一概念，并证明之。

定理 5.3.1。假设 $X\rightarrow Y \rightarrow Z$ 形成一个马尔可夫链，所以 $X \perp Z \mid Y$。接下来我们有 $\mathbb{I}(X;Y) \ge \mathbb{I}(X;Z)$。

证明。根据互信息的链式法则，我们可以用两种不同的方式展开互信息：

\[\begin{align} \mathbb{I}(X ; Y, Z) & =\mathbb{I}(X ; Z)+\mathbb{I}(X ; Y \mid Z) \tag{5.114} \\ & =\mathbb{I}(X ; Y)+\mathbb{I}(X ; Z \mid Y) \tag{5.115} \end{align}\]

考虑到 $X \perp Z \mid Y$，我们有 $\mathbb{I}(X ; Z \mid Y)=0$，所以

\[\mathbb{I}(X ; Z)+\mathbb{I}(X ; Y \mid Z)=\mathbb{I}(X ; Y) \tag{5.116}\]

考虑到 $\mathbb{I}(X ; Y \mid Z) \geq 0$，我们有 $\mathbb{I}(X ; Y) \geq \mathbb{I}(X ; Z)$。类似地，我们可以证明 $\mathbb{I}(Y ; Z) \geq \mathbb{I}(X ; Z)$。

5.3.4 充分统计量

DPI 的一个重要结论在于，假设我们有 $\theta \rightarrow X \rightarrow s(X)$。则

\[\mathbb{I}(\theta ; s(X)) \leq \mathbb{I}(\theta ; X) \tag{5.117}\]

如果等式成立，我们称 $s(X)$ 是一个用于预测 $\theta$ 的关于数据 $X$ 的充分统计量（sufficient statistic）。在这种情况下，我们可以等价地有 $\theta \rightarrow s(X) \rightarrow X$，因为我们可以从已知的 $s(X)$ 重构数据，同样可以从已知的参数 $\theta$ 精准地重构 $s(X)$。

充分统计量的一个例子是 $s(X)=X$，但这个统计量显然没有什么意义，因为它对数据完全没有一个概括总结。因此我们需要定义一个 最小充分统计量 $s(X)$，它首先是充分的，其次不包含关于 $\theta$ 的额外信息；所以 $s(X)$ 最大程度地对数据 $X$ 进行了压缩，同时不损失与预测 $\theta$ 相关的信息。更加正式的说，我们称 $s$ 是一个关于 $X$ 的最小统计量，如果对于某个函数 $f$ 和所有的充分统计量 $s^\prime(X)$，满足 $s(X)=f\left(s^{\prime}(X)\right)$。总结下来：

\[\theta \rightarrow s(X) \rightarrow s^{\prime}(X) \rightarrow X \tag{5.118}\]

此处， $s^\prime(X)$ 在 $s(X)$ 的基础上增加了冗余信息，所以形成了一个 one-to-many 的映射。

举个例子， $N$ 个伯努利实验的一个最小充分统计量就是 $N$ 和 $N_1=\Sigma_n\mathbb{I}(X_n=1)$ ，即，成功的次数。换句话说，我们不需要完整地记录整个实验结果序列以及它们的顺序，我们只需要记录总的试验次数。类似地，为了推理高斯分布（已知方差）的期望，我们只需要知道经验期望和样本的数量。

在第5.1.8节中，我们已经介绍了指数族分布的动机，即这些分布在某种意义上是最小的，因为它们除了包含对数据某些统计量的约束外，不携带其他信息。因此，用来生成指数族分布的统计量是充分的这一点是有道理的。这也暗示了Pitman-Koopman-Darmois定理更为显著的事实，该定理指出，对于任何具有固定域的分布而言，只有指数族分布能够在样本数量增加时允许具有有限维度的充分统计量[Dia88b]¹⁴。

5.3.5 多个变量之间的互信息

有几种方法将互信息推广到多元随机变量。

5.3.5.1 完全相关性

定义多变量 MI 的最简单方法是使用 完全相关性（total correlation）[Wat60][^Wat60] 或者 多信息（multi-information）[SV98][^SV98]

\[\begin{align} \mathbb{T C}\left(\left\{X_1, \ldots, X_D\right\}\right) & \triangleq D_{\mathbb{K L}}\left(p(\boldsymbol{x}) \| \prod_d p\left(x_d\right)\right) \tag{5.119}\\ & =\sum_{\boldsymbol{x}} p(\boldsymbol{x}) \log \frac{p(\boldsymbol{x})}{\prod_{d=1}^D p\left(x_d\right)}=\sum_d \mathbb{H}\left(x_d\right)-\mathbb{H}(\boldsymbol{x}) \tag{5.120} \end{align}\]

举个例子，对于 3 个随机变量，上式可以写成

\[\mathbb{T} \mathbb{C}(X, Y, Z)=\mathbb{H}(X)+\mathbb{H}(Y)+\mathbb{H}(Z)-\mathbb{H}(X, Y, Z) \tag{5.121}\]

其中 $\mathbb{H}(X, Y, Z)$ 表示联合熵

\[\mathbb{H}(X, Y, Z)=-\sum_x \sum_y \sum_z p(x, y, z) \log p(x, y, z) \tag{5.122}\]

可以证明完全相关性始终是非负的，且等于0的充要条件为 $p(\boldsymbol{x})=\prod_d p\left(x_d\right)$。然而，这意味着即使只有一对变量之间存在相互作用，完全相关性也不可能为零。例如，如果 $p(X, Y, Z) = p(X, Y)p(Z)$，那么完全相关性将是非零的，即使三者之间并没有相互作用。这也促使了第5.3.5.2节中交互信息的提出。

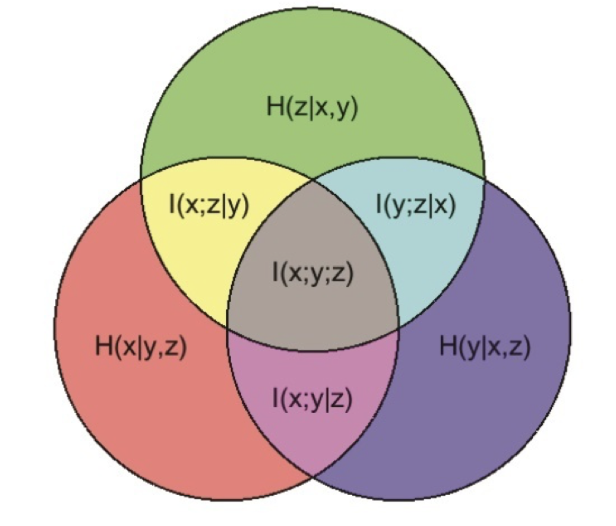
图 $5.7$：三个随机变量之间的多元互信息。

5.3.5.2 交互信息（Interaction information， co-information）

条件互信息可以用来给出多元互信息（multivariate mutual information，MMI）的归纳定义：

\[\mathbb{I}\left(X_1 ; \cdots ; X_D\right)=\mathbb{I}\left(X_1 ; \cdots ; X_{D-1}\right)-\mathbb{I}\left(X_1 ; \cdots ; X_{D-1} \mid X_D\right) \tag{5.123}\]

这被称为多元互信息（Multiple Mutual Information）[Yeu91b][^Yeu91b]，或协同信息（Co-information）[Bel03][^Bel03]。该定义与交互信息（Interaction Information）[McG54; Han80; JB03; Bro09] 在符号变化上是等价的。

对于3个变量，多元互信息（MMI）由以下公式给出：

\[\begin{align} \mathbb{I}(X ; Y ; Z) & =\mathbb{I}(X ; Y)-\mathbb{I}(X ; Y \mid Z) \tag{5.124}\\ & =\mathbb{I}(X ; Z)-\mathbb{I}(X ; Z \mid Y) \tag{5.125}\\ & =\mathbb{I}(Y ; Z)-\mathbb{I}(Y ; Z \mid X) \tag{5.126} \end{align}\]

这可以解释为在给定第三个变量的条件下，另外两对变量之间互信息的变化。需要注意的是，多元互信息关于输入的参数是对称的。

根据条件互信息的定义，我们有：

\[\mathbb{I}(X ; Z \mid Y)=\mathbb{I}(Z ; X, Y)-\mathbb{I}(Y ; Z) \tag{5.127}\]

所以我们可以将式 （5.125）重写成：

\[\mathbb{I}(X ; Y ; Z)=\mathbb{I}(X ; Z)+\mathbb{I}(Y ; Z)-\mathbb{I}(X, Y ; Z) \tag{5.128}\]

这告诉我们，多元互信息（MMI）是在单独以及联合给定 $X$ 和 $Y$ 的情况下，我们对 $Z$ 的了解程度的差异（另见第5.3.5.3节）。

图5.7的信息图展示了三元互信息（3-way MMI）的情况。当我们有多个变量时，解释此类图表的方法如下：阴影区域的面积，包括圆圈 $A,B,C$， 并排除圆圈 $F,G,H$，表示$\mathbb{I}(A ; B ; C ; \ldots \mid F, G, H, \ldots)$；如果 $B=C=\emptyset$，则表示 $\mathbb{H}(A \mid F, G, H, \ldots)$；如果 $F=G=H=\emptyset$，则表示 $\mathbb{I}(A ; B ; C, \ldots)$。

5.3.5.3 协同效应与冗余

多元互信息（MMI）定义为 $\mathbb{I}(X ; Y ; Z)=\mathbb{I}(X ; Z)+\mathbb{I}(Y ; Z)-\mathbb{I}(X, Y ; Z)$。我们可以看到，这个值可以是正的、零或负的。如果 $X$ 提供的关于 $Z$ 的部分信息也被 $Y$ 提供，那么 $X$ 和 $Y$ 之间（关于 $Z$）存在一定的冗余。在这种情况下，$\mathbb{I}(X ; Z)+\mathbb{I}(Y ; Z)>\mathbb{I}(X, Y ; Z)$，因此（根据公式 (5.128)）我们可以看到多元互信息将是正的。相反，如果我们通过同时观察 $X$ 和 $Y$ 来获得更多关于 $Z$ 的信息，我们说它们之间存在一定的协同效应。在这种情况下，$\mathbb{I}(X ; Z)+\mathbb{I}(Y ; Z)<\mathbb{I}(X, Y ; Z)$，此时多元互信息将是负的。

5.3.5.4 MMI 和因果

多元互信息（MMI）的符号可以用来区分不同类型的有向图模型，这些模型有时可以从因果关系的角度进行解释（关于因果关系的详细讨论，请参见第36章）。例如，考虑一个形式为 $X \leftarrow Z \rightarrow Y$ 的模型，其中 $Z$ 是 $X$ 和 $Y$ 的“原因”。例如，假设 $X$ 表示“正在下雨”这一事件，$Y$ 表示“天空是黑暗的”这一事件，而 $Z$ 表示“天空多云”这一事件。在给定共同原因 $Z$ 的条件下，子节点 $X$ 和 $Y$ 是独立的，因为如果我知道天空多云，注意到天空是黑暗的并不会改变我对是否会下雨的信念。因此，$\mathbb{I}(X ; Y \mid Z) \leq \mathbb{I}(X ; Y)$，所以 $\mathbb{I}(X ; Y ; Z) \geq 0$。

现在考虑 $Z$ 是一个共同效应（common effect）的情况，即 $X \rightarrow Z \leftarrow Y$。在这种情况下，由于“解释消除”（explaining away）现象（参见第4.2.4.2节），在给定 $Z$ 的条件下，$X$ 和 $Y$ 会变得依赖。例如，如果 $X$ 和 $Y$ 是独立的随机比特，而 $Z$ 是 $X$ 和 $Y$ 的异或（XOR），那么观察到 $Z=1$ 意味着$p(X \neq Y \mid Z=1)=1$，因此 $X$ 和 $Y$ 现在变得依赖（从信息论的角度，而非因果关系的角度），即使它们在先验上是独立的。因此，$\mathbb{I}(X ; Y \mid Z) \ge \mathbb{I}(X ; Y)$，所以$\mathbb{I}(X ; Y ; Z) \leq 0$。

最后，考虑一个马尔可夫链，$X \rightarrow Y \rightarrow Z$。我们有 $\mathbb{I}(X ; Z \mid Y) \leq \mathbb{I}(X ; Z)$，所以 MMI 必须是正数。

5.3.5.5 MMI和熵

我们也可以将 MMI 写成熵的形式。具体而言，已知

\[\mathbb{I}(X ; Y)=\mathbb{H}(X)+\mathbb{H}(Y)-\mathbb{H}(X, Y) \tag{5.129}\]

并且

\[\mathbb{I}(X ; Y \mid Z)=\mathbb{H}(X, Z)+\mathbb{H}(Y, Z)-\mathbb{H}(Z)-\mathbb{H}(X, Y, Z) \tag{5.130}\]

所以我们可以将式（5.124）重写成：

\[\mathbb{I}(X ; Y ; Z)=[\mathbb{H}(X)+\mathbb{H}(Y)+\mathbb{H}(Z)]-[\mathbb{H}(X, Y)+\mathbb{H}(X, Z)+\mathbb{H}(Y, Z)]+\mathbb{H}(X, Y, Z) \tag{5.131}\]

将此式与公式 (5.121) 进行对比。

更一般的情况，我们有

\[\mathbb{I}\left(X_1, \ldots, X_D\right)=-\sum_{\mathcal{T} \subseteq\{1, \ldots, D\}}(-1)^{|\mathcal{T}|} \mathbb{H}(\mathcal{T}) \tag{5.132}\]

对于大小为1、2和3的集合，其展开如下：

\[\begin{align} I_1 & =H_1 \tag{5.133}\\ I_{12} & =H_1+H_2-H_{12} \tag{5.134}\\ I_{123} & =H_1+H_2+H_3-H_{12}-H_{13}-H_{23}+H_{123} \tag{5.135} \end{align}\]

我们可以使用莫比乌斯反演公式（Möbius inversion formula）推导出以下关于变量集合 $\mathcal{S}$的对偶关系：

\[\mathbb{H}(\mathcal{S})=-\sum_{\mathcal{T} \subseteq \mathcal{S}}(-1)^{|\mathcal{T}|} \mathbb{I}(\mathcal{T}) \tag{5.136}\]

利用熵的链式法则，我们还可以推导出三元互信息（3-way MMI）的表达式：

\[\mathbb{I}(X ; Y ; Z)=\mathbb{H}(Z)-\mathbb{H}(Z \mid X)-\mathbb{H}(Z \mid Y)+\mathbb{H}(Z \mid X, Y) \tag{5.137}\]

5.3.6 互信息的变分确界

在本节中，我们将讨论计算互信息（MI）上下确界的方法，这些方法使用变分近似来处理难以处理的分布。这对于表示学习（第32章）非常有用。这种方法最早在 [BA03][^BA03] 中提出。关于互信息的变分确界更详细的综述，请参见 Poole 等人 [Poo+19b][^Poo19b]。

5.3.6.1 上确界

假设联合分布 $p(\boldsymbol{x}, \boldsymbol{y})$ 难以直接计算，但我们可以从 $p(\boldsymbol{x})$ 中进行采样并计算条件分布 $p(\boldsymbol{y} \mid \boldsymbol{x})$。此外，假设我们用 $q(\boldsymbol{y})$ 来近似 $p(\boldsymbol{y})$。那么，我们可以计算出互信息（MI）的一个上确界：

\[\begin{align} \mathbb{I}(\boldsymbol{x} ; \boldsymbol{y}) & =\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}\left[\log \frac{p(\boldsymbol{y} \mid \boldsymbol{x}) q(\boldsymbol{y})}{p(\boldsymbol{x}) q(\boldsymbol{y})}\right] \tag{5.138}\\ & =\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}\left[\log \frac{p(\boldsymbol{y} \mid \boldsymbol{x})}{q(\boldsymbol{y})}\right]-D_{\mathbb{K L}}(p(\boldsymbol{x}) \| q(\boldsymbol{y})) \tag{5.139}\\ & \leq \mathbb{E}_{p(\boldsymbol{x})}\left[\mathbb{E}_{p(\boldsymbol{y} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{y} \mid \boldsymbol{x})}{q(\boldsymbol{y})}\right]\right] \tag{5.140}\\ & =\mathbb{E}_{p(\boldsymbol{x})}\left[D_{\mathbb{K L}}(p(\boldsymbol{y} \mid \boldsymbol{x}) \| q(\boldsymbol{y}))\right] \tag{5.141} \end{align}\]

如果 $q(\boldsymbol{y})=p(\boldsymbol{y})$，那么上确界将是紧凑的。

这里的情况是，$\mathbb{I}(Y ; X)=\mathbb{H}(Y)-\mathbb{H}(Y \mid X)$，我们假设已知 $p(\boldsymbol{y} \mid \boldsymbol{x})$，因此可以很好地估计 $\mathbb{H}(Y \mid X)$。虽然我们不知道 $\mathbb{H}(Y)$，但可以使用某个模型 $q(\boldsymbol{y})$ 来近似它的上确界。考虑我们的模型永远无法比 $p(\boldsymbol{y})$ 本身更好（KL 散度的非负性），因此关于熵的估计会偏大，从而导致我们的互信息估计是一个上确界。

5.3.6.2 BA下确界

假设联合分布 $p(\boldsymbol{x}, \boldsymbol{y})$ 难以直接计算，但我们可以计算 $p(\boldsymbol{x})$。此外，假设我们用 $q(\boldsymbol{x} \mid \boldsymbol{y})$ 来近似 $p(\boldsymbol{x} \mid \boldsymbol{y})$。那么，我们可以推导出互信息的变分下确界：

\[\begin{align} \mathbb{I}(\boldsymbol{x} ; \boldsymbol{y}) & =\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}\left[\log \frac{p(\boldsymbol{x} \mid \boldsymbol{y})}{p(\boldsymbol{x})}\right] \tag{5.142}\\ & =\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}\left[\log \frac{q(\boldsymbol{x} \mid \boldsymbol{y})}{p(\boldsymbol{x})}\right]+\mathbb{E}_{p(\boldsymbol{y})}\left[D_{\mathbb{KL}}(p(\boldsymbol{x} \mid \boldsymbol{y}) \| q(\boldsymbol{x} \mid \boldsymbol{y}))\right] \tag{5.143} \\ & \geq \mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}\left[\log \frac{q(\boldsymbol{x} \mid \boldsymbol{y})}{p(\boldsymbol{x})}\right]=\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}[\log q(\boldsymbol{x} \mid \boldsymbol{y})]+h(\boldsymbol{x}) \tag{5.144} \end{align}\]

其中 $h(\boldsymbol{x})$ 是关于 $\boldsymbol{x}$ 的可微熵。上式被称为 BA 下确界，由 Barber 和 Agakov 命名[BA03][^BA03]。

5.3.6.3 NWJ下确界

BA下确界（Barber-Agakov下确界）要求一个可处理的归一化分布 $q(x \mid y)$，并且我们能逐点计算其值。如果以巧妙的方式对这一分布进行重参数化，我们可以得到一个不需要归一化分布的下确界。首先令：

\[q(\boldsymbol{x} \mid \boldsymbol{y})=\frac{p(\boldsymbol{x}) e^{f(\boldsymbol{x}, \boldsymbol{y})}}{Z(\boldsymbol{y})} \tag{5.145}\]

其中 $Z(\boldsymbol{y})=\mathbb{E}_{p(\boldsymbol{x})}\left[e^{f(\boldsymbol{x}, \boldsymbol{y})}\right]$ 表示归一化常数或配分函数。将其代入上述 BA 下界，我们得到：

\[\begin{align} \mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}\left[\log \frac{p(\boldsymbol{x}) e^{f(\boldsymbol{x}, \boldsymbol{y})}}{p(\boldsymbol{x}) Z(\boldsymbol{y})}\right] & =\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}[f(\boldsymbol{x}, \boldsymbol{y})]-\mathbb{E}_{p(\boldsymbol{y})}[\log Z(\boldsymbol{y})] \tag{5.146}\\ & =\mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}[f(\boldsymbol{x}, \boldsymbol{y})]-\mathbb{E}_{p(\boldsymbol{y})}\left[\log \mathbb{E}_{p(\boldsymbol{x})}\left[e^{f(\boldsymbol{x}, \boldsymbol{y})}\right]\right] \tag{5.147}\\ & \triangleq I_{D V}(X ; Y) \tag{5.148} \end{align}\]

这被称为 Donsker-Varadhan 下确界 [DV75][^DV75]。

利用对数函数可以用直线进行上确界逼近的事实，我们可以构造一个更易处理的版本

\[\log x \leq \frac{x}{a}+\log a-1 \tag{5.149}\]

如果我们令 $a=e$，我们有

\[\mathbb{I}(X ; Y) \geq \mathbb{E}_{p(\boldsymbol{x}, \boldsymbol{y})}[f(\boldsymbol{x}, \boldsymbol{y})]-e^{-1} \mathbb{E}_{p(\boldsymbol{y})} Z(\boldsymbol{y}) \triangleq I_{N W J}(X ; Y) \tag{5.150}\]

这被称为 NWJ 下界（以 Nguyen、Wainwright 和 Jordan 的作者命名 [NWJ10a][^NWJ10a]），或 f-GAN KL [NCT16a][^NCT16a]，或 MINE-f 分数 [Bel+18][^Bel18]。

5.3.6.4 InfoNCE下确界

如果我们对上述 DV 下确界进行多样本扩展，可以得到如下的下确界（推导过程请参考 [Poo+19b]）：

\[\begin{align} \mathbb{I}_{\mathrm{NCE}} & =\mathbb{E}\left[\frac{1}{K} \sum_{i=1}^K \log \frac{e^{f\left(\boldsymbol{x}_i, \boldsymbol{y}_i\right)}}{\frac{1}{K} \sum_{j=1}^K e^{f\left(\boldsymbol{x}_i, \boldsymbol{y}_j\right)}}\right] \tag{5.151}\\ & =\log K-\mathbb{E}\left[\frac{1}{K} \sum_{i=1}^K \log \left(1+\sum_{j \neq i}^K e^{f\left(\boldsymbol{x}_i, \boldsymbol{y}_j\right)-f\left(\boldsymbol{x}_i, \boldsymbol{y}_i\right)}\right)\right] \tag{5.152} \end{align}\]

其中期望是在联合分布 $p(X, Y)$ 下计算得到的。公式 (5.152) 被称为 InfoNCE 估计，由 [OLV18a; Hen+19a] 提出。（NCE 代表“噪声对比估计”，在第24.4节中讨论。）

这里的直觉是，互信息衡量的是联合分布 $p(\boldsymbol{x}, \boldsymbol{y})$ 和边缘分布乘积 $p(\boldsymbol{x})p(\boldsymbol{y})$ 之间的差异。换句话说，互信息衡量的是联合采样对 $(\boldsymbol{x}, \boldsymbol{y})$ 与独立采样 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的区别程度。公式 (5.152) 中的 InfoNCE 边界通过尝试训练一个模型来区分这两种情况，提供了对真实互信息的一个下界。

尽管这是一个有效的下确界，但如果互信息很大，我们可能需要使用较大的批次大小 $K$ 来估计 MI，因为 $\mathbb{I}_{\textrm{NCE}} ≤ \log K$。（最近 [SE20a] 提出使用多标签分类器而不是多类别分类器来克服这一限制。）

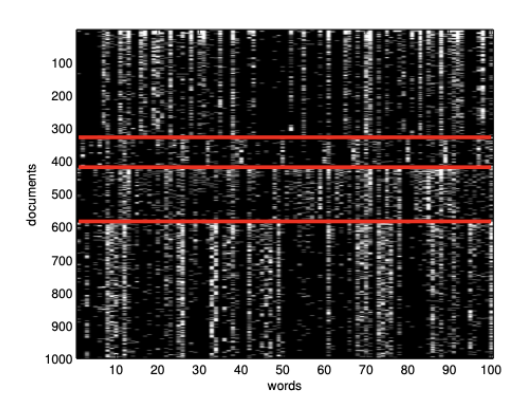
图 $5.8$：这是20-newsgroups数据的一个子集，大小为16242 x 100。为了清晰起见，我们只展示了1000行。每一行是一个文档（表示为词袋模型的二进制向量），每一列是一个单词。红色线条分隔了4个类别，这些类别按降序排列为：comp（计算机）、rec（娱乐）、sci（科学）、talk（讨论）（这些是USENET新闻组的标题）。我们可以看到，某些单词的存在或缺失能够指示文档的类别。数据可以从 http://cs.nyu.edu/~roweis/data.html 获取。代码由 newsgroups_visualize.ipynb 生成。。

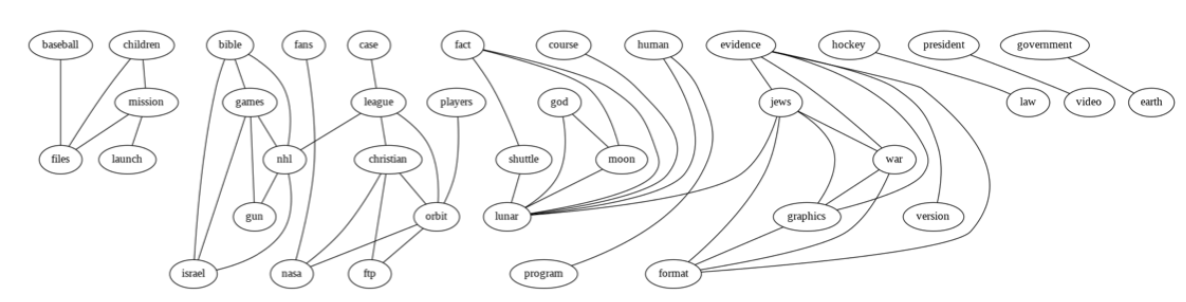
图 $5.9$：由20个新闻组数据构建的相关网络的一部分。数据如图5.8所示。我们展示了互信息大于或等于最大成对互信息20%的边。为了清晰起见，图表已被裁剪，因此我们只展示了一部分节点和边。由relevance_network_newsgroup_demo.ipynb生成。

5.3.7 Relevance networks

如果我们有一组相关变量，我们可以计算一个相关性网络（relevance network），在其中，如果两个变量之间的互信息 $\mathbb{I}\left(X_i ; X_j\right)$ 超过某个阈值，我们就在它们之间添加一条边 $i-j$。在高斯情况下，互信息 $\mathbb{I}\left(X_i ; X_j\right)=-\frac{1}{2} \log \left(1-\rho_{i j}^2\right)$，其中 $\rho_{i j}$ 是相关系数，生成的图称为协方差图（covariance graph，参见第4.5.5.1节）。然而，这种方法也可以应用于离散随机变量。

相关性网络在系统生物学中非常流行 [Mar+06]，用于可视化基因之间的相互作用。但它也可以应用于其他类型的数据集。例如，图5.9展示了20-newsgroup数据集中单词之间的互信息（MI），如图5.8所示。结果在直观上是合理的。

然而，相关性网络存在一个主要问题：图通常非常密集，因为大多数变量都与其他变量相关，即使对互信息进行了阈值处理。例如，假设 $X_1$ 直接影响 $X_2$，而 $X_2$ 又直接影响 $X_3$（例如，这些变量形成一个信号级联 $X_1-X_2-X_3$）。那么 $X_1$ 与 $X_3$ 之间的互信息不为零（反之亦然），因此除了 1−2 和 2−3 边之外，还会有一条 1−3 边；因此，根据阈值的选择，图可能是完全连通的。

解决这个问题的方法是学习一个概率图模型（probabilistic graphical model），它表示条件独立性，而不是相关性。在上述链式例子中，由于 $X_1 \perp X_3 \mid X_2$，因此不会存在 1−3 边。因此，图模型通常比相关性网络稀疏得多。详见第30章。

5.4 数据压缩（Data compression (source coding)）

数据压缩（Data compression），也称为信源编码（source coding），是信息论的核心。它也与概率机器学习有关。原因如下：如果我们能够对不同类型的数据样本的概率进行建模，那么我们可以为最常见的样本分配较短的编码词，而将较长的编码留给较少出现的样本。这类似于自然语言中的情况，常见的词汇（如“a”、“the”、“and”）通常比罕见词汇要短得多。因此，压缩数据的能力需要发现数据中的潜在模式及其相对的频率。这促使Marcus Hutter提出将压缩作为一种衡量通用人工智能性能的客观方法。更具体地说，他提供50,000欧元奖励给任何能够将前100MB的（英文）维基百科数据压缩得比某个基准更好的人。这就是所谓的Hutter奖。

在本节中，我们将简要总结数据压缩的一些关键思想。详细内容请参见例如[Mac03; CT06; YMT22]。

5.4.1 无损压缩

离散数据，例如自然语言，总是可以以一种能够唯一恢复原始数据的方式进行压缩。这被称为无损压缩（lossless compression）。

克劳德·香农证明了从分布 $p$ 中产生的数据进行无损编码所需的预期比特数至少为 $\mathbb{H}(p)$。这就是所谓的信源编码定理（source coding theorem）。要达到这个下界，需要提出好的概率模型以及基于这些模型设计编码的好方法。由于KL散度的非负性，$\mathbb{H}{ce}(p, q) ≥ \mathbb{H}(p)$，因此如果我们使用任何不同于真实模型 $p$ 的模型 $q$ 来压缩数据，将会使用一些额外的比特。额外比特的数量正好等于 $D\mathbb{KL}(p ∥ q)$。

实现无损编码的常见技术包括霍夫曼编码、算术编码和非对称数字系统 [Dud13]。这些算法的输入是一个字符串上的概率分布（这也是机器学习发挥作用的地方）。这种分布通常使用潜在变量模型来表示（参见例如 [TBB19; KAH19]）。

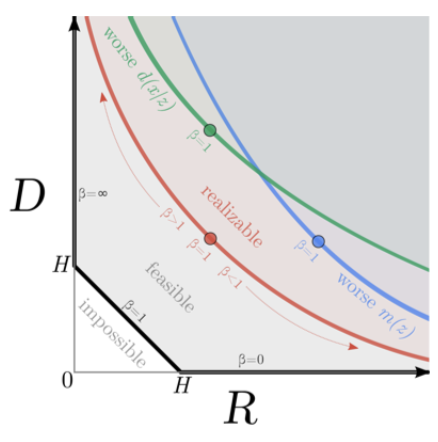
图 $5.10$：率-失真曲线。

5.4.2 有损压缩和率失真权衡(here)

为了将连续的实值信号（如图像和声音）编码为数字信号，首先需要将连续信号量化为离散的符号。一种简单的方法是使用矢量量化。然后，我们可以使用无损编码的方法压缩这个离散的符号序列。然而，在解压缩的过程中，我们会丢失掉一些信息。因此，这种方法被称为有损压缩（lossy compression）。

在本节中，我们将讨论表征大小（即使用的离散符号的数量）与重构误差之间的权衡。我们将使用5.6.2节中讨论的变分信息瓶颈的术语（区别在于此处是在无监督的设定）。具体而言，我们假设有一个随机编码器 $p(\boldsymbol{z} \mid \boldsymbol{x})$，一个随机解码器 $d(\boldsymbol{x} \mid \boldsymbol{z})$ 和一个先验分布 $m(\boldsymbol{z})$。

我们定义编码器-解码器配对的失真（distortion）（如5.6.2节所述）为：

\[D=-\int d \boldsymbol{x} p(\boldsymbol{x}) \int d \boldsymbol{z} \ e(\boldsymbol{z} \mid \boldsymbol{x}) \log d(\boldsymbol{x} \mid \boldsymbol{z}) \tag{5.153}\]

如果解码器是一个判别式模型加高斯噪声，即$d(\boldsymbol{x} \mid \boldsymbol{z})=\mathcal{N}\left(\boldsymbol{x} \mid f_d(\boldsymbol{z}), \sigma^2\right)$，同时编码器也是判别式的，即$e(\boldsymbol{z} \mid \boldsymbol{x})=\delta\left(\boldsymbol{z}-f_e(\boldsymbol{x})\right)$。则上式变成

\[D=\frac{1}{\sigma^2} \mathbb{E}_{p(\boldsymbol{x})}\left[\left\|f_d\left(f_e(\boldsymbol{x})\right)-\boldsymbol{x}\right\|^2\right] \tag{5.154}\]

这被称为期望重构误差（reconstruction error）。

我们定义模型的率（rate）为：

\[\begin{align} R & =\int d \boldsymbol{x} p(\boldsymbol{x}) \int d \boldsymbol{z} e(\boldsymbol{z} \mid \boldsymbol{x}) \log \frac{e(\boldsymbol{z} \mid \boldsymbol{x})}{m(\boldsymbol{z})} \tag{5.155}\\ & =\mathbb{E}_{p(\boldsymbol{x})}\left[D_{\mathbb{KL}}(e(\boldsymbol{z} \mid \boldsymbol{x}) \| m(\boldsymbol{z}))\right] \tag{5.156}\\ & =\int d \boldsymbol{x} \int d \boldsymbol{z} p(\boldsymbol{x}, \boldsymbol{z}) \log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{p(\boldsymbol{x}) m(\boldsymbol{z})} \geq \mathbb{I}(\boldsymbol{x}, \boldsymbol{z}) \tag{5.157} \end{align}\]

上式实际上是编码分布与边际分布之间的平均 KL 散度。如果我们使用 $m(\boldsymbol{z})$ 而不是真正的聚合后验分布 $p(\boldsymbol{z})=\int d \boldsymbol{x} p(\boldsymbol{x}) e(\boldsymbol{z} \mid \boldsymbol{x})$ 来编码我们的数据，则率 是我们使用前者所需要付出的额外比特数。

率和失真之间存在一个基本的权衡。为了理解这一点，考虑一个简单的编码方案，令 $e(\boldsymbol{z} \mid \boldsymbol{x})=\delta(\boldsymbol{z}-\boldsymbol{x})$，这实际上就是使用 $\boldsymbol{x}$ 作为它自身的最佳表征。这种方案会导致 0 失真（从而最大化似然），但会带来很高的率，因为每个 $e(\boldsymbol{z} \mid \boldsymbol{x})$ 分布都是唯一的，并且远离先验分布 $m(\boldsymbol{z})$。换句话说，这不会有任何压缩效果。相反，如果设置 $e(\boldsymbol{z} \mid \boldsymbol{x})=\delta(\boldsymbol{z}-\mathbf{0})$，编码器将忽略输入本身的信息。在这种情况下，率会是 0，但失真会很高。

我们可以使用第5.3.6节中互信息的变分下限和上限更精确地描述率与失真之间的权衡：

\[H-D \leq \mathbb{I}(\boldsymbol{x} ; \boldsymbol{z}) \leq R \tag{5.158}\]

其中 $H$ 表示（可微）熵

\[H=-\int d \boldsymbol{x} p(\boldsymbol{x}) \log p(\boldsymbol{x}) \tag{5.159}\]

对于离散数据，所有概率的上限都是 1，因此熵 $H \geq 0$ 且 $D \geq 0$。此外，率总是非负的 $R \geq 0$，因为它是 KL 散度的平均值（这对于离散或连续编码 $\boldsymbol{z}$ 都成立。）。因此，我们可以绘制出 $R$ 和 $D$ 之间的集合，如图 5.10 所示。这被称为率失真曲线（rate distortion curve）。

底部的水平线对应于零失真，即 $D=0$，在这种情况下，我们可以完美地编码和解码数据。这可以通过使用简单的编码器实现，即 $e(\boldsymbol{z} \mid \boldsymbol{x})=\delta(\boldsymbol{z}-\boldsymbol{x})$。香农的信源编码定理告诉我们，在这种设置下，我们需要使用的最小比特数是数据的熵，因此当 $D=0$ 时，$R \geq H$。如果我们使用次优的边际分布 $m(\boldsymbol{z})$ 进行编码，将会增加率而不影响失真。

左侧的垂直线对应于零率，即 $R=0$，在这种情况下，隐编码 $\boldsymbol{z}$ 与输入数据 $\boldsymbol{x}$ 无关。同时，解码器 $d(\boldsymbol{x} \mid \boldsymbol{z})$ 也与 $\boldsymbol{z}$ 无关。然而，我们仍然可以学习一个不使用隐编码的联合概率模型 $p(\boldsymbol{x})$，例如，这可以是一个自回归模型。这种模型能够达到的最小失真——也就是数据的熵，即 $D \geq H$。

黑色对角线展示了满足 $D=H-R$ 的解，其中上下界是紧凑的。在实际应用中，我们无法达到对角线上的点，因为这要求上下界都是紧凑的，即假设我们的模型 $e(\boldsymbol{z} \mid \boldsymbol{x})$ 和 $d(\boldsymbol{x} \mid \boldsymbol{z})$ 是完美的。这被称为“非参数极限”[^非]。在数据有限的实际场景中，我们总会引入额外的误差，所以率失真图会描绘出一条向上偏移的曲线，如图 5.10 所示。

通过最小化以下目标，我们可以沿着这条曲线生成不同的解决方案：

\[J=D+\beta R=\int d \boldsymbol{x} p(\boldsymbol{x}) \int d \boldsymbol{z} e(\boldsymbol{z} \mid \boldsymbol{x})\left[-\log d(\boldsymbol{x} \mid \boldsymbol{z})+\beta \log \frac{e(\boldsymbol{z} \mid \boldsymbol{x})}{m(\boldsymbol{z})}\right] \tag{5.160}\]

如果我们令 $\beta=1$，同时定义 $q(\boldsymbol{z} \mid \boldsymbol{x})=e(\boldsymbol{z} \mid \boldsymbol{x}), p(\boldsymbol{x} \mid \boldsymbol{z})=d(\boldsymbol{x} \mid \boldsymbol{z})$，以及 $p(\boldsymbol{z})=m(\boldsymbol{z})$，这与第21.2节中的VAE目标完全一致。为了理解这一点，请注意，第10.1.1.2节中的ELBO可以写成

\[\mathrm{£}=-(D+R)=\mathbb{E}_{p(\boldsymbol{x})}\left[\mathbb{E}_{e(\boldsymbol{z} \mid \boldsymbol{x})}[\log d(\boldsymbol{x} \mid \boldsymbol{z})]-\mathbb{E}_{e(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{e(\boldsymbol{z} \mid \boldsymbol{x})}{m(\boldsymbol{z})}\right]\right] \tag{5.161}\]

我们认为这是重构误差期望减去KL项 $D_{\mathbb{KL}}(e(\boldsymbol{z} \mid \boldsymbol{x}) | m(\boldsymbol{z}))$。

如果我们允许 $\beta \neq 1$，我们就可以得到在21.3.1节中讨论的 $\beta$-VAE（变分自编码器）的优化目标。然而需要注意的是，$\beta$-VAE 模型无法区分对角线上的不同解，因为这些解都满足 $\beta=1$。这是因为所有这些模型具有相同的边际似然（因此具有相同的ELBO，即模型对数据的拟合能力相同），尽管它们在是否学习到有意义的潜在表示方面可能有显著差异。因此，如21.3.1节所讨论的，似然并不是比较无监督表示学习方法质量的充分指标。

有关率、失真和感知之间固有冲突的进一步讨论，请参阅[BM19][^BM19]。关于评估模型率失真曲线的技术，请参见[HCG20][^HCG20]。

5.4.3 Bits back 编码

在上一节中，我们使用平均KL散度来惩罚编码的率，$\mathbb{E}_{p(\boldsymbol{x})}[R(\boldsymbol{x})]$，其中

\[R(\boldsymbol{x}) \triangleq \int d \boldsymbol{z} p(\boldsymbol{z} \mid \boldsymbol{x}) \log \frac{p(\boldsymbol{z} \mid \boldsymbol{x})}{m(\boldsymbol{z})}=\mathbb{H}_{c e}(p(\boldsymbol{z} \mid \boldsymbol{x}), m(\boldsymbol{z}))-\mathbb{H}(p(\boldsymbol{z} \mid \boldsymbol{x})) . \tag{5.162}\]

第一项是交叉熵，它表示编码 $\boldsymbol{x}$ 所需的期望比特数；第二项是熵，它表示所需的最小比特数。因此，我们惩罚的是将编码传递给接收者所需的额外比特数。为什么我们不需要为实际使用的总比特数（即交叉熵）“付费”呢？

原因是我们原则上可以将最优编码所需的信息比特数“拿回来”；这被称为比特回馈编码（bits back coding） [HC93; FH97]。其论证过程如下：假设 Alice 试图（无损地）向 Bob 传输一些数据，例如一张图像 $\boldsymbol{x}$。在他们分开之前，Alice 和 Bob 决定共享他们的编码器 $p(\boldsymbol{z} \mid \boldsymbol{x})$、边缘分布 $m(\boldsymbol{z})$ 和解码器分布 $d(\boldsymbol{x} \mid \boldsymbol{z})$。为了传输图像，Alice 将使用两双部编码（two part code）。首先，她会从编码器中采样一个编码 $\boldsymbol{z} \sim p(\boldsymbol{z} \mid \boldsymbol{x})$，并通过一个专门设计用于高效编码来自边缘分布 $m(\boldsymbol{z})$ 的样本的信道将其传输给 Bob；这需要花费 $-\log _2 m(\boldsymbol{z})$ 比特。接下来，Alice 会使用她的解码器 $d(\boldsymbol{x} \mid \boldsymbol{z})$ 计算残差，并以 $-\log _2 d(\boldsymbol{x} \mid \boldsymbol{z})$ 比特的成本无损地将其发送给 Bob。这里所需的预期总比特数是我们最初预期的：：

\[\mathbb{E}_{p(\boldsymbol{z} \mid \boldsymbol{x})}\left[-\log _2 d(\boldsymbol{x} \mid \boldsymbol{z})-\log _2 m(\boldsymbol{z})\right]=D+\mathbb{H}_{c e}(p(\boldsymbol{z} \mid \boldsymbol{x}), m(\boldsymbol{z})) . \tag{5.163}\]

我们看到，这实际上是失真加上交叉熵，而不是失真加上率。那么，我们如何拿回这些比特，将交叉熵转换为率呢？

诀窍在于鲍勃实际上接收到了比我们预想的更多的信息。Bob可以使用编码 $\boldsymbol{z}$ 和残差完美地重构 $\boldsymbol{x}$。然而，Bob还知道Alice发送的具体编码 $\boldsymbol{z}$，以及她使用的编码器 $p(\boldsymbol{z} \mid \boldsymbol{x})$。当Alice从 $p(\boldsymbol{z} \mid \boldsymbol{x})$ 中抽取编码 $\boldsymbol{z}$ 时，她必须使用某种熵源来生成随机样本。假设她通过从《白鲸记》（Moby Dick）的压缩副本中依次选择单词来生成随机比特流。在Bob这边，他可以逆向工程所有的采样比特，从而恢复《白鲸记》的压缩副本！因此，Alice可以利用选择 $\boldsymbol{z}$ 时的额外随机性来共享更多信息。

虽然在最初的表述中，bits back 的论点主要是理论性的，提供了一种思想实验来解释为什么我们应该用 KL 散度而不是交叉熵来惩罚模型，但最近已经开发了几种实际算法，真正实现了 bits back 的目标。这些算法包括 [HPHL19; AT20; TBB19; YBM20; HLA19; FHHL20]。

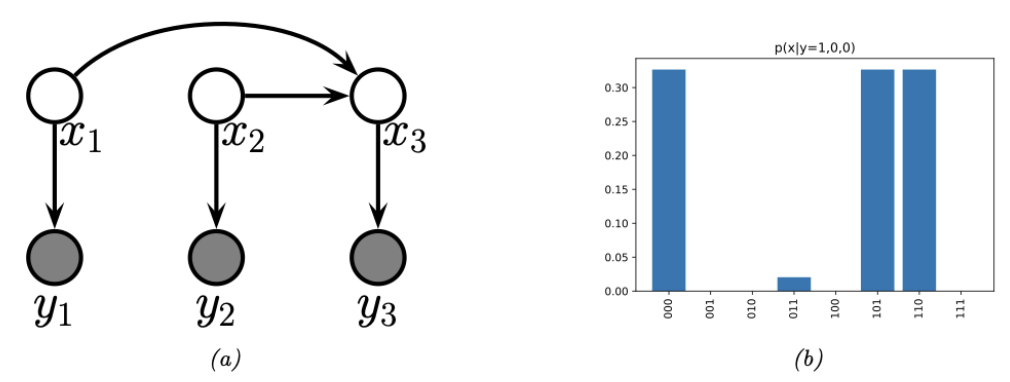
图 $5.11$：a）一个简单的纠错码 DPGM（Directed Probabilistic Graphical Model，有向概率图模型）。$x_i$ 是发送的比特，$y_i$ 是接收的比特。$x_3$ 是从 $x_1$ 和 $x_2$ 计算出的偶校验位。（b）给定 $\boldsymbol{y}=(1,0,0)$时，码字的后验分布；比特翻转的概率为 0.2。由 error_correcting_code_demo.ipynb 生成。

5.5 误差-矫正编码（信道编码）

纠错编码（error correcting codes）背后的思想是向信号 $\boldsymbol{x}$（这是对原始数据进行编码后的结果）中注入冗余，使得当信号通过噪声信道（例如手机连接）传输到接收端时，接收端能够从任何可能发生的损坏中恢复信号。这被称为信道编码（channel coding）。

更详细地说，设 $\boldsymbol{x} \in{0,1}^m$ 是源消息，其中 $m$ 称为块长度（block length）。设 $\boldsymbol{y}$ 是将 $\boldsymbol{x}$ 通过噪声信道发送后的结果。这是一个被破坏的消息版本。例如，每个消息位可能会以概率 $\alpha$ 独立翻转，在这种情况下，$p(\boldsymbol{y} \mid \boldsymbol{x})=\prod_{i=1}^m p\left(y_i \mid x_i\right)$，其中 $p\left(y_i \mid x_i=0\right)=[1-\alpha, \alpha]$ 和 $p\left(y_i \mid x_i=1\right)=[\alpha, 1-\alpha]$。或者，我们可以添加高斯噪声，因此 $p\left(y_i \mid x_i=b\right)=\mathcal{N}\left(y_i \mid \mu_b, \sigma^2\right)$。接收端的目标是从噪声观测中推断出真正的消息，即计算 $\operatorname{argmax}_{\boldsymbol{x}} p(\boldsymbol{x} \mid \boldsymbol{y})$。

提高恢复原始信号可能性的一种常见方法是在发送信号之前向其添加奇偶校验位。这些校验位是原始信号的确定性函数，用于指定输入比特的总和是奇数还是偶数。这提供了一种冗余形式，因此如果一个比特被损坏，我们仍然可以推断其值，假设其他比特没有被翻转。（这是合理的，因为我们假设比特是独立随机损坏的，因此多个比特被翻转的可能性低于单个比特被翻转的可能性。）

例如，假设我们有两个原始消息比特，并添加一个奇偶校验位。这可以使用有向图模型来表示，如图 5.11(a) 所示。该图编码了以下联合概率分布：

\[p(\boldsymbol{x}, \boldsymbol{y})=p\left(x_1\right) p\left(x_2\right) p\left(x_3 \mid x_1, x_2\right) \prod_{i=1}^3 p\left(y_i \mid x_i\right) \tag{5.164}\]

先验概率 $p\left(x_1\right)$ 和 $p\left(x_2\right)$ 表示均匀分布。条件项 $p\left(x_3 \mid x_1, x_2\right)$ 是确定性的，用于计算 $\left(x_1, x_2\right)$ 的奇偶校验值。具体来说，如果 $x_{1: 2}$ 中 1 的数量是奇数，则有 $p\left(x_3=1 \mid x_1, x_2\right)=1$。似然项 $p\left(y_i \mid x_i\right)$表示一个比特翻转噪声信道模型，噪声水平为 $\alpha=0.2$，表示每个比特在传输过程中有 20% 的概率被翻转。

假设我们观察到 $\boldsymbol{y}=(1,0,0)$。我们知道这不可能是发送端发送的内容，因为这违反了奇偶校验约束（如果 $x_1=1$，那么我们知道 $x_3=1$）。相反，$\boldsymbol{x}$ 的三个后验模式是 000（第一个比特被翻转）、110（第二个比特被翻转）和 101（第三个比特被翻转）。后验中唯一具有非零支持的其他配置是 011，这对应于三个比特都被翻转的不太可能的假设（见图 5.11(b)）。所有其他假设（001、010 和 100）与用于创建码字的确定性方法不一致。（有关此点的进一步讨论，请参见第 9.3.3.2 节。）。

在实践中，我们使用更复杂的编码方案，这些方案效率更高，因为它们向消息中添加的冗余位更少，但仍然能够保证错误可以被纠正。更多细节请参见第 9.4.8 节。

5.6 信息瓶颈（The information bottleneck）

在本节中，我们将使用随机瓶颈（stochastic bottleneck）来防止在判别模型 $p(\boldsymbol{y} \mid \boldsymbol{x})$上的过拟合，进而提高鲁棒性和校准性。

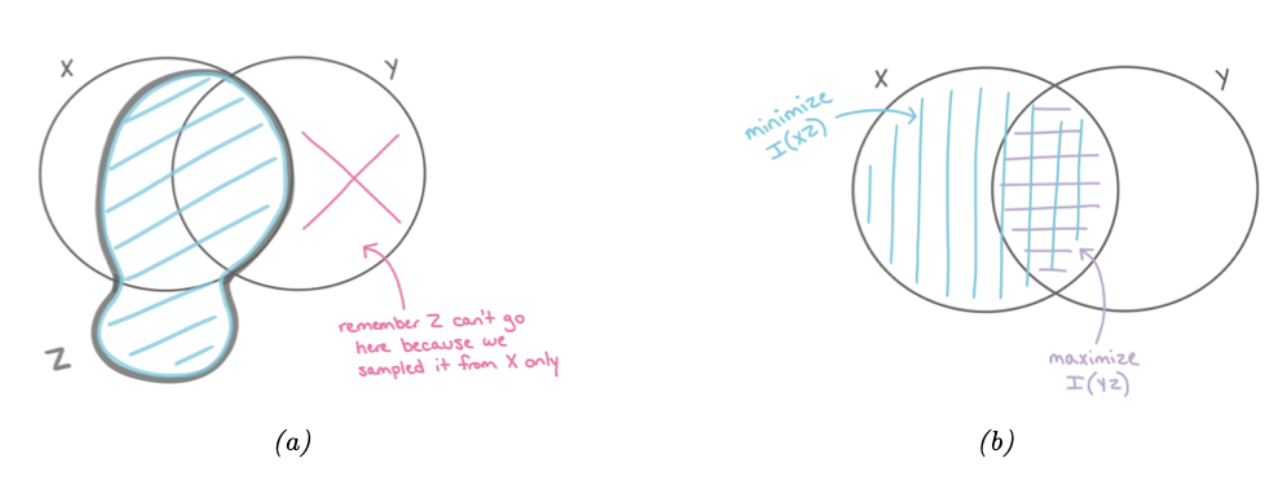
图 $5.12$：信息瓶颈的信息图。（a）$Z$ 可以包含关于 $X$ 的任意数量的信息（无论这些信息是否对预测 $Y$ 有用），但它不能包含与 $X$ 不共享的关于 $Y$ 的信息。（b）$Z$ 的最优表示最大化 $\mathbb{I}(Z, Y)$ 并最小化 $\mathbb{I}(Z, X)$。经 Katie Everett 许可使用。。

5.6.1 基础版的信息瓶颈

我们称 $\boldsymbol{z}$ 是 $\boldsymbol{x}$ 的一种表征，如果 $\boldsymbol{z}$ 是关于 $\boldsymbol{x}$ 的（可能是随机的）函数，该函数可以通过条件概率 $p(\boldsymbol{z} \mid \boldsymbol{x})$ 来描述。我们称$\boldsymbol{x}$的表示$\boldsymbol{z}$ 对于任务$\boldsymbol{y}$是充分的，如果满足 $\boldsymbol{y} \perp \boldsymbol{x} \mid \boldsymbol{z}$，或者等价地，如果 $\mathbb{I}(\boldsymbol{z} ; \boldsymbol{y})=\mathbb{I}(\boldsymbol{x} ; \boldsymbol{y})$，即$\mathbb{H}(\boldsymbol{y} \mid \boldsymbol{z})=\mathbb{H}(\boldsymbol{y} \mid \boldsymbol{x})$。我们称一个表示是最小充分统计量（minimal sufficient statistic），如果 $\boldsymbol{z}$ 是充分的，并且没有其他的 $\boldsymbol{z}$ 具有更小的 $\mathbb{I}(\boldsymbol{z} ; \boldsymbol{x})$ 。因此，我们希望找到一个表示 $\boldsymbol{z}$，它在最大化 $\mathbb{I}(\boldsymbol{z} ; \boldsymbol{y})$ 的同时最小化 $\mathbb{I}(\boldsymbol{z} ; \boldsymbol{x})$。也就是说，我们希望优化以下目标：

\[\min \beta \mathbb{I}(\boldsymbol{z} ; \boldsymbol{x})-\mathbb{I}(\boldsymbol{z} ; \boldsymbol{y}) \tag{5.165}\]

其中 $\beta \geq 0$，我们通过优化分布 $p(\boldsymbol{z} \mid \boldsymbol{x})$ 和 $p(\boldsymbol{y} \mid \boldsymbol{z})$来实现上述的优化目标。这被称为**信息瓶颈原理 **（information bottleneck principle）[TPB99][^TPB99]。该原理将最小充分统计量的概念进行了推广，考虑了充分性与最小性之间的权衡，这种权衡反映在拉格朗日乘子 $\beta>0$。

图5.12得到了阐释信息瓶颈原理。我们假设 $Z$ 是关于$X$ 的一个函数，且与 $Y$ 独立，即我们假设图模型为 $Z \leftarrow X \leftrightarrow Y$。这对应于以下的联合分布：

\[p(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z})=p(\boldsymbol{z} \mid \boldsymbol{x}) p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x}) \tag{5.166}\]

因此，$Z$ 可以捕获关于 $X$ 的任何量的信息，但不能包含 $Y$ 独有的信息，如图 5.12a 所示。最优的表示仅捕获对 $Y$ 有用的 $X$ 信息；为了防止我们“浪费容量”并拟合 $X$ 中不相关的细节，$Z$ 还应尽量减少关于 $X$ 的信息，如图 5.12b 所示。

如果所有的随机变量都是离散的，并且 $\boldsymbol{z}=e(\boldsymbol{x})$ 是关于 $\boldsymbol{x}$ 的确定性函数，那么可以使用[TPB99][^TPB99]的算法来最小化第5.6节中的信息瓶颈（IB）目标。如果所有变量都服从联合高斯分布，该目标存在解析解[Che+05]（这种方法可以视为一种有监督PCA）。但一般来说，精确解决这个问题是棘手的。我们将在第5.6.2节讨论一种可行的近似方法。（更多细节可以参考例如[SZ22][^SZ22]。）

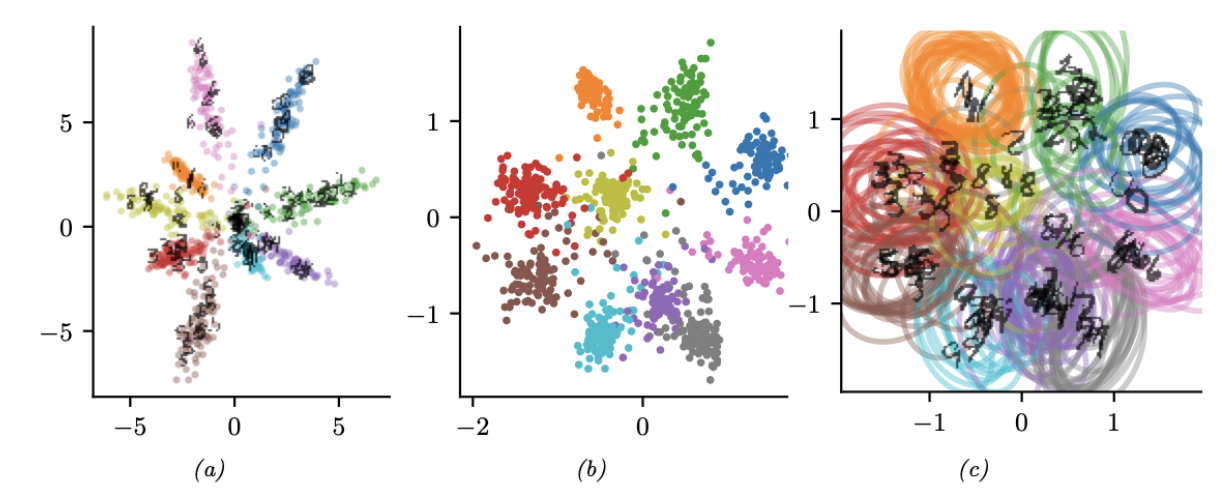
图 $5.13$：由 MLP 分类器生成的 MNIST 数字的二维嵌入。（a）确定性模型。（b-c）VIB 模型，均值和协方差。由 vib_demo.ipynb 生成。经 Alex Alemi 许可使用。

5.6.2 变分 IB

在本节中，我们将利用第5.3.6节的思想，推导出方程（5.165）的一个变分上界。这被称为变分信息瓶颈（Variational IB，VIB）方法[Ale+16]。关键技巧是利用KL散度的非负性：

\[\int d \boldsymbol{x} p(\boldsymbol{x}) \log p(\boldsymbol{x}) \geq \int d \boldsymbol{x} p(\boldsymbol{x}) \log q(\boldsymbol{x}) \tag{5.167}\]

对于任何分布$q$成立。（注意，$p$ 和 $q$ 都可能以其他变量为条件。）

为了更详细地解释该方法，定义以下符号。设 $e(\boldsymbol{z} \mid \boldsymbol{x})=p(\boldsymbol{z} \mid \boldsymbol{x})$ 表示编码器，$b(\boldsymbol{z} \mid \boldsymbol{y}) \approx p(\boldsymbol{z} \mid \boldsymbol{y})$ 表示反向编码器，$d(\boldsymbol{y} \mid \boldsymbol{z}) \approx p(\boldsymbol{y} \mid \boldsymbol{z})$ 表示分类器（解码器），$m(\boldsymbol{z}) \approx p(\boldsymbol{z})$ 表示边际分布。（注意，我们可以自由选择 $p(\boldsymbol{z} \mid \boldsymbol{x})$，即编码器，但其他分布是关于联合分布 $p(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z})$ 的边际分布和条件分布的近似。）此外，设⟨·⟩表示在联合分布 $p(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{z})$ 的某些项下求解期望。

利用上述符号，我们可以推导出 $\mathbb{I}(\boldsymbol{z} ; \boldsymbol{y})$ 的下界：

\[\begin{align} \mathbb{I}(\boldsymbol{z} ; \boldsymbol{y}) & =\int d \boldsymbol{y} d \boldsymbol{z} p(\boldsymbol{y}, \boldsymbol{z}) \log \frac{p(\boldsymbol{y}, \boldsymbol{z})}{p(\boldsymbol{y}) p(\boldsymbol{z})} \tag{5.168}\\ & =\int d \boldsymbol{y} d \boldsymbol{z} p(\boldsymbol{y}, \boldsymbol{z}) \log p(\boldsymbol{y} \mid \boldsymbol{z})-\int d \boldsymbol{y} d \boldsymbol{z} p(\boldsymbol{y}, \boldsymbol{z}) \log p(\boldsymbol{y}) \tag{5.169}\\ & =\int d \boldsymbol{y} d \boldsymbol{z} p(\boldsymbol{z}) p(\boldsymbol{y} \mid \boldsymbol{z}) \log p(\boldsymbol{y} \mid \boldsymbol{z})-\text { const } \tag{5.170}\\ & \geq \int d \boldsymbol{y} d \boldsymbol{z} p(\boldsymbol{y}, \boldsymbol{z}) \log d(\boldsymbol{y} \mid \boldsymbol{z}) \tag{5.171}\\ & =\langle\log d(\boldsymbol{y} \mid \boldsymbol{z})\rangle \tag{5.172} \end{align}\]

其中我们利用了 $\mathbb{H}(p(\boldsymbol{y}))$ 是与表征 $\boldsymbol{z}$ 无关的常数。

考虑到式（5.172）是关于分布 $p(\boldsymbol{y}, \boldsymbol{z})$ 求解期望，所以可以通过如下的分布进行采样样本 $(\boldsymbol{y}, \boldsymbol{z})$ 对的采样

\[p(\boldsymbol{y}, \boldsymbol{z})=\int d \boldsymbol{x} p(\boldsymbol{x}) p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{z} \mid \boldsymbol{x})=\int d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{y}) e(\boldsymbol{z} \mid \boldsymbol{x}) \tag{5.173}\]

上式的右侧表示，先随机采样得到 $(\boldsymbol{x},\boldsymbol{y})$ 的配对，然后在通过编码器 $e$ 得到对应的 $\boldsymbol{z}$。

类似的，我们可以推导出 $\mathbb{I}(\boldsymbol{z} ; \boldsymbol{x})$ 的上确界：

\[\begin{align} \mathbb{I}(\boldsymbol{z} ; \boldsymbol{x}) & =\int d \boldsymbol{z} d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{z}) \log \frac{p(\boldsymbol{z}, \boldsymbol{x})}{p(\boldsymbol{x}) p(\boldsymbol{z})} \tag{5.174} \\ & =\int d \boldsymbol{z} d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{z}) \log p(\boldsymbol{z} \mid \boldsymbol{x})-\int d \boldsymbol{z} p(\boldsymbol{z}) \log p(\boldsymbol{z}) \tag{5.175} \\ & \leq \int d \boldsymbol{z} d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{z}) \log p(\boldsymbol{z} \mid \boldsymbol{x})-\int d \boldsymbol{z} p(\boldsymbol{z}) \log m(\boldsymbol{z}) \tag{5.176}\\ & =\int d \boldsymbol{z} d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{z}) \log \frac{e(\boldsymbol{z} \mid \boldsymbol{x})}{m(\boldsymbol{z})} \tag{5.177} \\ & =\langle\log e(\boldsymbol{z} \mid \boldsymbol{x})\rangle-\langle\log m(\boldsymbol{z})\rangle \tag{5.178} \end{align}\]

需要注意的是我们可以通过从 $p(\boldsymbol{x}, \boldsymbol{z})=p(\boldsymbol{x}) p(\boldsymbol{z} \mid \boldsymbol{x})$ 采样来近似期望。

综上所述，我们得到了信息瓶颈（IB）优化目标的上界：

\[\beta \mathbb{I}(\boldsymbol{x} ; \boldsymbol{z})-\mathbb{I}(\boldsymbol{z} ; \boldsymbol{y}) \leq \beta(\langle\log e(\boldsymbol{z} \mid \boldsymbol{x})\rangle-\langle\log m(\boldsymbol{z})\rangle)-\langle\log d(\boldsymbol{y} \mid \boldsymbol{z})\rangle \tag{5.179}\]

所以 VIB 目标是

\[\begin{align} \mathcal{L}_{\mathrm{VIB}} & =\beta\left(\mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{x}) e(\boldsymbol{z} \mid \boldsymbol{x})}[\log e(\boldsymbol{z} \mid \boldsymbol{x})-\log m(\boldsymbol{z})]\right)-\mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{x}) e(\boldsymbol{z} \mid \boldsymbol{x}) d(\boldsymbol{y} \mid \boldsymbol{z})}[\log d(\boldsymbol{y} \mid \boldsymbol{z})] \tag{5.180}\\ & =-\mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{x}) e(\boldsymbol{z} \mid \boldsymbol{x}) d(\boldsymbol{y} \mid \boldsymbol{z})}[\log d(\boldsymbol{y} \mid \boldsymbol{z})]+\beta \mathbb{E}_{p_{\mathcal{D}}(\boldsymbol{x})}\left[D_{\mathbb{K L}}(e(\boldsymbol{z} \mid \boldsymbol{x}) \| m(\boldsymbol{z}))\right] \tag{5.181} \end{align}\]

现在，我们可以使用随机梯度下降法（SGD）对其进行最小化（相对于编码器、解码器和边缘分布的参数）。(我们假设这些分布是可重参数化的，正如第6.3.5节所讨论的那样)。对于编码器 $e(\boldsymbol{z} \mid \boldsymbol{x})$，我们通常使用条件高斯分布，而对于解码器 $d(\boldsymbol{y} \mid \boldsymbol{z})$，我们通常使用softmax分类器。对于边缘分布 $m(\boldsymbol{z})$，我们应该使用一个灵活的模型，例如高斯混合模型，因为它需要近似聚合后验分布（aggregated posterior） $p(\boldsymbol{z})=\int d \boldsymbol{z p}(\boldsymbol{x}) e(\boldsymbol{z} \mid \boldsymbol{x})$，这是一个由 $N$ 个高斯分布组成的混合体（假设 $p(\boldsymbol{x})$ 是一个包含 $N$ 个样本的经验分布，且 $e(\boldsymbol{z} \mid \boldsymbol{x})$ 是高斯分布）。

图5.13中对此进行了说明，其中我们将一个多层感知器（MLP）模型拟合到MNIST数据集上。在传递到softmax之前，我们使用了一个2维的瓶颈层。在图a中，我们展示了一个确定性编码器学习到的嵌入。我们看到每张图像被映射到一个点，且类别之间或实例之间的重叠很少。在图b-c中，我们展示了一个随机编码器学习到的嵌入。每张图像被映射到一个高斯分布，我们分别展示了均值和协方差。类别仍然被很好地分开，但类别的个别实例不再可区分，因为这些信息对于预测目的并不重要。

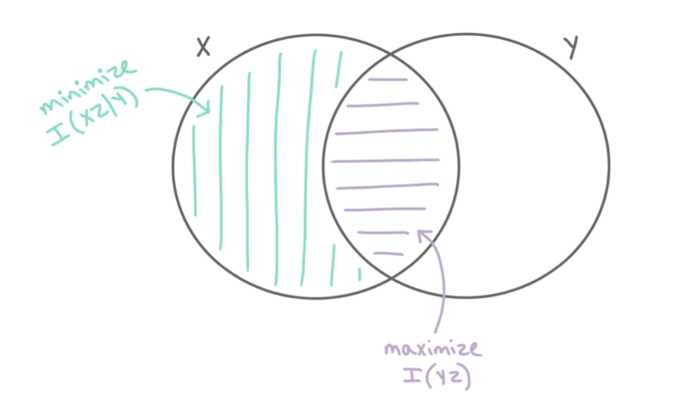
图 $5.14$：条件熵瓶颈（Conditional Entropy Bottleneck, CEB）选择一种表示 $Z$，以最大化 $\mathbb{I}(Z, Y)$ 并最小化 $\mathbb{I}(X, Z \mid Y)$。经 Katie Everett 授权使用。

5.6.3 条件熵瓶颈

信息瓶颈（IB）方法试图在最大化 $\mathbb{I}(Z ; Y)$ 的同时最小化 $\mathbb{I}(Z ; X)$。我们可以将此目标写作：

\[\min \mathbb{I}(\boldsymbol{x} ; \boldsymbol{z})-\lambda \mathbb{I}(\boldsymbol{y} ; \boldsymbol{z}) \tag{5.182}\]

其中 $\lambda \ge 0$。然而，我们从图5.12b中的信息图中可以看出，$\mathbb{I}(Z ; X)$ 包含了一些与 $Y$ 相关的信息。一个合理的替代目标是最小化剩余互信息 $\mathbb{I}(X ; Z \mid Y)$。这引出了以下目标函数：

\[\min \mathbb{I}(\boldsymbol{x} ; \boldsymbol{z} \mid \boldsymbol{y})-\lambda^{\prime} \mathbb{I}(\boldsymbol{y} ; \boldsymbol{z}) \tag{5.183}\]

其中 $\lambda^{\prime} \geq 0$。这被称为条件熵瓶颈（Conditional Entropy Bottleneck，简称CEB）[Fis20]。图5.14展示了这一概念的示意图。

由于 $\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z} \mid \boldsymbol{y})=\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z})-\mathbb{I}(\boldsymbol{y} ; \boldsymbol{z})$，我们可以看到CEB与标准IB在 $\lambda^{\prime}=\lambda+1$ 时是等价的。然而，相比于$\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z})$，$\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z} \mid \boldsymbol{y})$ 更容易被上界化，因为我们在条件中引入了$\boldsymbol{y}$，这提供了关于$\boldsymbol{z}$的信息。具体而言，通过利用 $p(\boldsymbol{z} \mid \boldsymbol{x}, \boldsymbol{y})=p(\boldsymbol{z} \mid \boldsymbol{x})$，我们得出：

\[\begin{align} \mathbb{I}(\boldsymbol{x} ; \boldsymbol{z} \mid \boldsymbol{y}) & =\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z})-\mathbb{I}(\boldsymbol{y} ; \boldsymbol{z}) \tag{5.184}\\ & =\mathbb{H}(\boldsymbol{z})-\mathbb{H}(\boldsymbol{z} \mid \boldsymbol{x})-[\mathbb{H}(\boldsymbol{z})-\mathbb{H}(\boldsymbol{z} \mid \boldsymbol{y})] \tag{5.185}\\ & =-\mathbb{H}(\boldsymbol{z} \mid \boldsymbol{x})+\mathbb{H}(\boldsymbol{z} \mid \boldsymbol{y}) \tag{5.186}\\ & =\int d \boldsymbol{z} d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{z}) \log p(\boldsymbol{z} \mid \boldsymbol{x})-\int d \boldsymbol{z} d \boldsymbol{y} p(\boldsymbol{z}, \boldsymbol{y}) \log p(\boldsymbol{z} \mid \boldsymbol{y}) \tag{5.187}\\ & \leq \int d \boldsymbol{z} d \boldsymbol{x} p(\boldsymbol{x}, \boldsymbol{z}) \log e(\boldsymbol{z} \mid \boldsymbol{x})-\int d \boldsymbol{z} d \boldsymbol{y} p(\boldsymbol{z}, \boldsymbol{y}) \log b(\boldsymbol{z} \mid \boldsymbol{y}) \tag{5.188}\\ & =\langle\log e(\boldsymbol{z} \mid \boldsymbol{x})\rangle-\langle\log b(\boldsymbol{z} \mid \boldsymbol{y})\rangle \tag{5.189} \end{align}\]

综上所述，我们得到了最终的CEB目标函数：

\[\min \beta(\langle\log e(\boldsymbol{z} \mid \boldsymbol{x})\rangle-\langle\log b(\boldsymbol{z} \mid \boldsymbol{y})\rangle)-\langle\log d(\boldsymbol{y} \mid \boldsymbol{z})\rangle \tag{5.190}\]

值得注意的是，通常学习条件反向编码器 $b(\boldsymbol{z} \mid \boldsymbol{y})$ 比学习无条件边缘分布 $m(\boldsymbol{z})$ 更为容易。此外，我们知道当 $\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z} \mid \boldsymbol{y})=\mathbb{I}(\boldsymbol{x} ; \boldsymbol{z})-\mathbb{I}(\boldsymbol{y} ; \boldsymbol{z})=0$ 时，上界达到最紧。对应的 $\beta$ 值代表了一个最优的表示。相比之下，在使用信息瓶颈（IB）时，如何衡量与最优状态的距离并不明确。

5.7 算法信息论

我们目前讨论的信息理论基于底层随机分布的特性，该分布被假设为生成观测数据的来源。然而，从许多方面来看，它并未捕捉到大多数人直观理解的“信息”概念。例如，考虑一个由均匀伯努利分布独立生成的$n$位序列。该分布每个元素的最大熵为 $H_2(0.5)=1$，因此长度为 $n$ 的序列的编码长度为 \(-\log _2 p(\mathcal{D} \mid \theta)=-\sum_{i=1}^n \log _2 \operatorname{Ber}\left(x_i \mid \theta=0.5\right)=n\)。然而，直观上，这样的序列并不包含太多信息。

有一种替代方法可以量化给定序列中的信息量（与随机模型的信息内容相对），称为算法信息论（algorithmic information theory）。这一理论的根源由几位作者独立发展[Sol64; Kol65; Cha66; Cha69]。我们在下面提供一个简要概述。更多细节，请参阅例如[Hut07; GV08; LV19]。

5.7.1 柯尔莫哥洛夫复杂度（Kolmogorov Complexity）

算法信息论中的关键概念是比特字符串 $\boldsymbol{x}=\boldsymbol{x}_{1: n}$ 的柯尔莫哥洛夫复杂度（Kolmogorov complexity），它被定义为能够生成字符串 $\boldsymbol{x}$ 的最短计算机程序 $p$ 的长度：\(K(\boldsymbol{x})=\min _{p \in \mathcal{B}^*}[\ell(p): U(\boldsymbol{p})=\boldsymbol{x}]\) ，其中 $\mathcal{B}^*$ 表示任意长的比特字符串集合，$\ell(p)$ 表示程序 $p$ 的长度，$U$ 表示通用图灵机（universal Turing machine）（这个复杂度的定义可以从比特字符串 $\boldsymbol{x}$ 扩展到函数 $f$，但细节相当复杂。）可以证明，柯尔莫哥洛夫复杂度具有许多类似于香农熵的性质。例如，如果我们忽略加法常数以简化讨论，可以证明 \(K(\boldsymbol{x} \mid \boldsymbol{y}) \leq K(\boldsymbol{x}) \leq K(\boldsymbol{x}, \boldsymbol{y})\)，这与 $H(X \mid Y) \leq H(X) \leq H(X, Y)$ 类似。

不幸的是，柯尔莫哥洛夫复杂度不是一个可计算的函数。然而，可以通过在柯尔莫哥洛夫复杂度中添加一个（对数级）时间复杂度项，从而得到列文复杂度（Levin complexity） [Lev73]，它是可以计算的。列文复杂度定义为：$L(\boldsymbol{x})=\min _{p \in \mathcal{B}^*}[\ell(p)+\log (\operatorname{time}(p)): U(\boldsymbol{p})=\boldsymbol{x}]$ ，其中 $\operatorname{time}(p)$是程序 $p$ 的运行时间。Levin复杂度可以通过时间分片的方式运行所有程序来计算，即为每个程序$p$ 分配时间 $2^{-\ell(p)}$ ，直到第一个程序运行结束并输出 $\boldsymbol{x}$；这种方法被称为列文搜索（Levin search）或通用搜索（universal search），并且需要的时间为 $\operatorname{time}(L S(\boldsymbol{x}))=2^{L(\boldsymbol{x})}$。

尽管列文复杂度是可计算的，但它仍然效率低下（尽管已经取得了一些进展 [Sch03]）。然而，我们也可以通过参数化近似来实现更高效地计算 $K(\boldsymbol{x})$的上界。例如，假设 $q$ 是关于比特字符串上的分布。可以证明 $K(\boldsymbol{x}) \leq-\log q(\boldsymbol{x})+K(q)$，其中 $K(q)$ 是分布（函数）$q$ 的K-复杂度。如果$q$ 是一个参数模型，我们可以通过$q$ 参数的编码长度来近似 $K(q)$；这等价于第 3.8.7.1 节讨论的最小描述长度（Minimum Description Length，MDL）目标。

我们可以利用Kolmogorov复杂度来给出单个序列（或数据集）随机性的正式定义，而无需引入随机变量或通信信道的概念。具体来说，如果一个字符串 $\boldsymbol{x}$ 的最短描述比字符串本身短（即，如果 $K(\boldsymbol{x})<\ell(\boldsymbol{x})=n$），则称该字符串是可压缩的；否则，我们称该字符串是算法随机（algorithmically random）的。（这种随机性称为马丁-洛夫随机性（Martin-Löf randomness） [ML66]，以区别于其他类型的随机性。）例如，$\boldsymbol{x}=(10101010 \cdots)$ 显然是可压缩的，因为它只是重复模式 10；字符串 $\boldsymbol{x}=(11001001 \cdots)$ 也是可压缩的（尽管程度较低），因为它是 $\pi^2$ 的二进制展开；然而，$x=(10110110 \cdots)$ 是“真正随机的”，因为它源自真空中的量子波动（参见 [HQC24, Sec 2.7.1]）。

除了理论上的意义外，上述“单个序列”的信息论方法还为（其中包括）著名的Lempel-Ziv无损数据压缩方案 [ZL77] 奠定了基础，该案是zip编码的核心。（详见 [Mer24]）。进一步地，这种方法还可以用于实现一种通用相似性度量（universal similarity metric） [Li+04]。

\[d(\boldsymbol{x}, \boldsymbol{y})=\frac{\max [K(\boldsymbol{x} \mid \boldsymbol{y}), K(\boldsymbol{y} \mid \boldsymbol{x})]}{\max [K(\boldsymbol{x}), K(\boldsymbol{y})]} \tag{5.191}\]

其中，诸如 $K(\boldsymbol{x})$ 这样的术语可以通过一些通用压缩器（如LZ）的编码成本来近似，这催生了归一化压缩距离（normalized compression distance） [CV05]。最近的研究 [Jia+23] 表明，在“低资源”限制下，NCD 结合 K-近邻算法（K-Nearest Neighbors, KNN）在文本分类任务中可以超越BERT语言模型的表现（尽管词袋分类器在这种环境下也表现良好，且速度更快 [Opi23]）。。

5.7.2 所罗门诺夫归纳（Solomonoff Induction）

现在考虑（在线）预测问题。假设我们已经观察到从某个未知分布 $\mu\left(x_{1: t}\right)$ 中抽取的序列 \(\boldsymbol{x}_{1: t}\)；我们希望用某种模型 $\nu$ 来近似 $\mu$，从而能够利用 \(\nu\left(x_{t+1} \mid \boldsymbol{x}_{1: t}\right)\) 预测未来。这被称为归纳问题（problem of induction）。我们假设 $\nu \in \mathcal{M}$，其中 $\mathcal{M}$ 是一个可数的模型（分布）集合。令 $w_\nu$ 为模型 $\nu$ 的先验概率。在所罗门诺夫归纳（Solomonoff induction） [Sol64] 方法中，我们假设 $\mathcal{M}$ 是所有可计算函数的集合，并定义先验为 $w_\nu=2^{-K(\nu)}$。这是一个“通用先验”，因为它可以模拟任何可计算的分布 $\mu$。此外，这种特定的加权项受奥卡姆剃刀原理（Occam’s razor）的启发，该原理指出我们应该选择能够解释数据的最简单模型。

给定这个先验（或实际上任何其他先验），我们可以使用以下贝叶斯混合模型来计算序列上的先验预测分布：

\[\xi\left(\boldsymbol{x}_{1: t}\right)=\sum_{\nu \in \mathcal{M}} w_\nu \nu\left(\boldsymbol{x}_{1: t}\right) \tag{5.192}\]

从这个先验预测分布，我们可以在第 $t$步计算后验预测分布：

\[\begin{align} \xi\left(x_t \mid \boldsymbol{x}_{<t}\right) & =\frac{\xi\left(\boldsymbol{x}_{1: t}\right)}{\xi\left(\boldsymbol{x}_{<t}\right)}=\frac{\sum_{\nu \in \mathcal{M}} w_\nu \nu\left(\boldsymbol{x}_{1: t}\right)}{\xi\left(\boldsymbol{x}_{<t}\right)}=\sum_{\nu \in \mathcal{M}} w_\nu \frac{\nu\left(\boldsymbol{x}_{1: t}\right)}{\xi\left(\boldsymbol{x}_{<t}\right)} \tag{5.193} \\ & =\sum_{\nu \in \mathcal{M}} w_\nu \frac{\nu\left(\boldsymbol{x}_{<t}\right)}{\xi\left(\boldsymbol{x}_{<t}\right)} \nu\left(x_t \mid \boldsymbol{x}_{<t}\right)=\sum_{\nu \in \mathcal{M}} w\left(\nu \mid \boldsymbol{x}_{<t}\right) \nu\left(x_t \mid \boldsymbol{x}_{<t}\right) \tag{5.194} \end{align}\]

在最后一行中，我们利用了每个模型的后验权重由以下公式给出的事实：

\[w\left(\nu \mid \boldsymbol{x}_{1: t}\right)=p\left(\nu \mid \boldsymbol{x}_{1: t}\right)=\frac{p(\nu) p\left(\boldsymbol{x}_{1: t} \mid \nu\right)}{p\left(\boldsymbol{x}_{1: t}\right)}=\frac{w_\nu \nu\left(\boldsymbol{x}_{1: t}\right)}{\xi\left(\boldsymbol{x}_{1: t}\right)} \tag{5.195}\]

现在考虑在每一步 $t$ 比较这个预测分布与真实值的准确性。我们将使用平方误差来进行比较：

\[s_t\left(\boldsymbol{x}_{<t}\right)=\sum_{x_t \in \mathcal{X}}\left(\mu\left(x_t \mid \boldsymbol{x}_{<t}\right)-\xi\left(x_t \mid \boldsymbol{x}_{<t}\right)\right)^2 \tag{5.196}\]

考虑直到时间 $n$ 的总误差期望：

\[S_n=\sum_{t=1}^n \sum_{\boldsymbol{x}_{<t} \in \mathcal{X}^{t-1}} \mu\left(\boldsymbol{x}_{<t}\right) s_t\left(\boldsymbol{x}_{<t}\right) \tag{5.197}\]

在 [Sol78] 中，Solomonoff 证明了其预测器在极限情况下的总误差的以下显著界限：

\[S_{\infty} \leq \ln \left(w_\mu^{-1}\right)=K(\mu) \ln 2 \tag{5.198}\]

这表明总误差受到生成数据的环境复杂性的限制。因此，简单的环境更容易学习（从样本复杂性的角度来看），因此最优预测器的预测会迅速接近真实值。

我们还可以考虑一种假设数据是由某个未知的确定性程序 $p$ 生成的设定。这个程序必须满足 $U(p)=x *$，其中 $\boldsymbol{x} *$是观测到的前缀 $\boldsymbol{x}=\boldsymbol{x}_{1: t}$ 的无限扩展。假设我们将程序的先验定义为 $\operatorname{Pr}(p)=2^{-\ell(p)}$。那么序列上的先验预测分布由以下公式给出 [Sol64]：

\[M(\boldsymbol{x})=\sum_{p: U(p)=\boldsymbol{x} *} 2^{-\ell(p)} \tag{5.199}\]

值得注意的是，可以证明（见例如 [WSH13]），$M(\boldsymbol{x})=\xi(\boldsymbol{x})$。由此，我们可以计算后验预测分布 \(M\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{<t}\right)=M\left(\boldsymbol{x}_{1: t}\right) / M\left(\boldsymbol{x}_{<t}\right)\)。由于这是一个确定性分布的凸组合，它也可以用于模拟随机环境。

由于所罗门诺夫归纳依赖于柯尔莫哥洛夫复杂度来定义其先验，因此它是不可计算的。然而，可以通过各种方法对其进行近似。例如，最近的研究 [GM+24] 表明，可以使用元学习（见第 19.6.4 节）训练一个通用序列预测器，如 Transformer 或 LSTM，通过在由随机图灵机生成的数据上进行训练，使得 Transformer 学会近似一个通用预测器。

5.7.3 AIXI 和通用人工智能（AGI）

在 [Hut05] 中，Marcus Hutter 将 Solomonoff 归纳法扩展到在线决策智能体的场景中，该智能体需要在未知环境中采取行动以最大化未来的预期奖励（类似于强化学习，在第35章中讨论）。如果我们使用滚动时域控制策略（见第 35.4.1 节），每一步的最优行动是最大化后验预期未来奖励的行动（未来 $m$ 步的奖励）。如果我们假设智能体将未知环境表示为一个程序 $p \in \mathcal{M}$，并使用 Solomonoff 先验，那么最优策略由以下期望最大化公式给出：

\[a_t=\underset{a_t}{\operatorname{argmax}} \sum_{o_t, r_t} \cdots \max _{a_m} \sum_{o_m, r_m}\left[r_t+\cdots+r_m\right] \sum_{p: U\left(p, a_{1: m}\right)=\left(o_1 r_1 \cdots o_m r_m\right)} 2^{-\ell(p)} \tag{5.200}\]

其中 $U$ 是通用图灵机。这个智能体被称 AIXI，其中“AI”代表“人工智能（Artificial Intelligence）”，而“XI”指的是Solomonoff 归纳法中使用的希腊字母 $\xi$。当然，AIXI 智能体在实际计算上是不可行的，但可以设计各种近似方法。例如，我们可以使用蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS，见第 35.4.1.2 节）来近似期望最大化（expectimax）。或者，我们可以使用时序差分学习（Temporal Difference Learning, TD-learning，见第 35.2.2 节）来学习策略（以避免对行动序列的搜索）；在策略混合中的加权项要求智能体预测其自身的未来行动，因此这种方法被称为自AIXI（self-AIXI）[Cat+23]。

AIXI 智能体被称为“可能的最智能通用智能体”[HQC24]，并且可以被视为（通用）人工通用智能（Artificial General Intelligence, AGI）的理论基础。

1. 贝叶斯推理和其他统计学习方法中，信念更新是指根据新的观测数据调整对某个假设或模型的信任度。 ↩

2. ↩

3. ↩ ↩² ↩³

4. ↩

5. ↩

6. ↩

7. ↩

8. ↩

9. ↩

10. ↩

11. ↩

12. ↩

13. ↩

14. ↩