本章,我们将介绍扩散模型,漫长的调试
- 25.1 简介
- 25.2 降噪扩散概率模型(DDPMs)
- 25.3 Score-based 生成模型(SGMs)
- 25.4 使用微分方程建模连续时间模型
- 25.5 加速扩散模型
- 25.6 条件生成
- 25.7 离散隐空间内的扩散模型
25.1 简介
本章,我们将讨论扩散模型(diffusion model)。这类生成模型最近引起了广泛关注,因为它能够生成多样且高质量的样本,同时由于训练方法相对简单,使得训练一个超大规模的扩散模型成为可能。接下来,我们将会看到,扩散模型与VAE(第21章),归一化流(第23章)以及EBM(第24章)存在着密切关联。
扩散模型背后的基本思想主要是基于如下的观察:将噪声转换成具备结构化特征的正常数据很难,但将正常数据转换成噪声却很容易。具体而言,通过反复执行随机编码器 \(q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)\),执行 \(T\) 步后,我们可以逐渐将观察到的正常数据 \(\boldsymbol{x}_0\) 转换成对应的噪声版本 \(\boldsymbol{x}_T\),且如果 \(T\) 足够大, \(\boldsymbol{x}_T\sim\mathcal{N}(\mathbf{0},\mathbf{I})\),或者其他一些方便分析的参考分布,这个将正常数据转化成噪声的过程被称为 前向过程(forwards process)或 扩散过程(diffusion process)。接下来,我们可以学习一个逆向过程(reverse process)来反转前向过程——即通过执行解码器 \(p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t\right)\) $T$ 步,将噪声转换成正常的数据 \(\boldsymbol{x}_0\)。图25.1展示了上述两个过程。在以下内容中,我们将更详细地讨论扩散模型。我们的讨论基于[KGV22]1的优秀教程。更多细节可以参考最近的综述论文[Yan+22]2; [Cao+22]3以及专业论文[Kar+22][^Kar22]。还有许多其他优秀的在线资源,如 https://github.com/heejkoo/Awesome-Diffusion-Models 和 https://scorebasedgenerativemodeling.github.io/。更多的数学内容,可以参考[McA23]4。

图25.1:降噪概率扩散模型。前向过程使用(无可学习参数)推理网络;该过程只是在每一个时间节点增加噪声。逆向过程使用解码器,这是一个可学习的高斯模型。图片引用自[KGV22]1。经Arash Vahdat允许后使用。
25.2 降噪扩散概率模型(DDPMs)
本节,我们将讨论降噪扩散概率模型(Denoising diffusion probabilistic models,DDPM),该模型首先在[SD+15b]5中被提出,并在[HJA20]6; [Kin+21]7和许多其他工作中进行了扩展。我们可以将DDPM看作类似于分层变分自编码器(第21.5节)的模型,区别在于,在扩散模型中,所有的隐变量(表示为 $\boldsymbol{x}_t$,$t=1:T$)与输入$\boldsymbol{x}_0$具有相同的维度。(在维度是否一致方面,DDPM又类似于第23章的归一化流,然而,在扩散模型中,隐层的输出是随机的,并且不需要使用可逆变换。)此外,编码器 $q$ 是一个简单的线性高斯模型,而不是通过学习得到的8,解码器 $p$ 在不同时间节点(timestep)之间共享模型参数。这些限制使得我们可以获得一个非常简单的训练目标,进而使更深层的模型训练变得简单,从而避免了后验坍塌(第21.4节)的风险。特别是在第25.2.3节中,我们将看到,扩散模型的优化最终可以归结为加权版本的非线性最小二乘问题。
25.2.1 编码器(前向扩散)
在扩散模型中,前向编码过程定义了一个简单的线性高斯模型:
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)=\mathcal{N}\left(\boldsymbol{x}_t \mid \sqrt{1-\beta_t} \boldsymbol{x}_{t-1}, \beta_t \mathbf{I}\right) \tag{25.1}\]其中, $\beta_t \in (0,1)$ 取决于噪声时间表(noise schedule,25.2.4节进行讨论)。以输入$\boldsymbol{x}_0$为条件,所有中间过程产生的隐变量的服从的联合概率分布定义为:
\[q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)=\prod_{t=1}^T q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right) \tag{25.2}\]由于上式定义了一个线性高斯马尔可夫链,我们可以计算任意时间节点隐变量的边际分布,该分布具有封闭解。具体而言,我们有
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\mathcal{N}\left(\boldsymbol{x}_t \mid \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) \tag{25.3}\]其中我们定义:
\[\alpha_t \triangleq 1-\beta_t, \bar{\alpha}_t=\prod_{s=1}^t \alpha_s \tag{25.4}\]我们可以选择一种噪声时间表使得 $\bar{\alpha}_T \approx 0$,这样 $q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \approx \mathcal{N}(\textbf{0}, \textbf{I})$。
实际上,分布 $q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)$ 又被称为扩散核(diffusion kernel)。将其应用于输入的数据分布并计算无条件边际分布,这个过程等同于高斯卷积:
\[q\left(\boldsymbol{x}_t\right)=\int q_0\left(\boldsymbol{x}_0\right) q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right) d \boldsymbol{x}_0 \tag{25.5}\]如图25.2所示,随着 $t$ 的增加,上述的边际分布会变得越来越简单。在图像领域,这个过程首先会消除图像中的高频信息(即低级的细节,如纹理),随后会消除低频信息(即高级的或“语义级别的”信息,如形状),如图25.1所示。
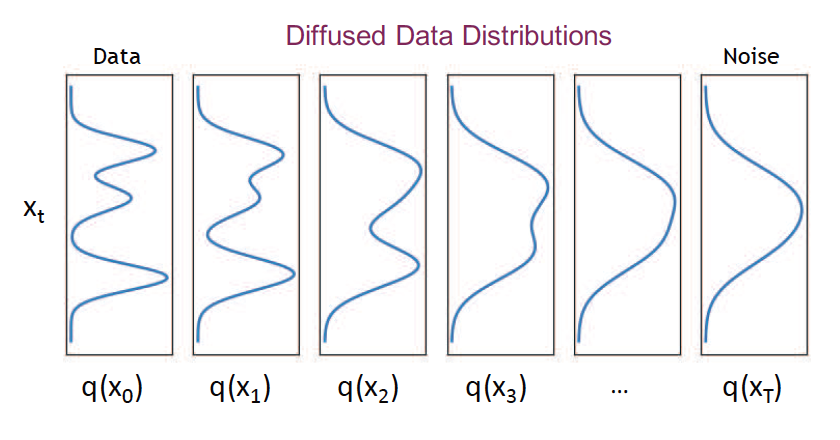
图25.2: 1维数据下的扩散模型示意图。前向过程逐渐将经验分布 $q(\boldsymbol{x}_0)$ 转换成一个简单的目标分布,此处即 $q\left(\boldsymbol{x}_T\right)=\mathcal{N}(\mathbf{0}, \mathbf{I})$。为了从模型中生成样本,我们采样一个样本 $\boldsymbol{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ ,然后执行马尔可夫链的反向过程 \(\boldsymbol{x}_t \sim p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t+1}\right)\),直到我们得到原始输入空间的样本 $\boldsymbol{x}_0$。图片引用自 [KGV22]1。经Arash Vahdat允许后使用。
| 译者注(关于噪声时间表如何定义) |
在 DDPM 中,作者使用了线性的变换方式定义$\beta_t$。具体而言,作者令 $T=1000$,$\beta_1=10^{-4}, \beta_T=0.02$。任意时刻的 $\beta_t$ 由如下方式生成:
1
torch.linspace(beta_start, beta_end, timesteps) # timesteps=T, beta_start=beta_1, beta_end=beta_T
作者选择这么做的动机为:
1
These constants were chosen to be small relative to data scaled to [−1, 1], ensuring that reverse and forward processes have approximately the same functional form while keeping the signal-to-noise ratio at xT as small as possible.
具体而言,在扩散模型中,需要确保每一步所加的噪声都要足够小,这样才能确保前向过程和逆向过程具备相同的函数形式,只有在这个前提下,我们才有可能使逆向过程可解。另外,通常情况下,我们假设最终的含噪分布(先验分布)是一个标准正态分布,所以我们需要使 $x_T$ 的信噪比足够小,即 $q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \approx \mathcal{N}(\textbf{0}, \textbf{I})$。
线性变换的形式相对简单,但也存在一些问题,在 《Improved Denoising Diffusion Probabilistic Models》中,作者指出,线性变换导致 $\bar{\alpha}_t$ 存在突变,如图N25.1所示,线性变换的情况下,$\bar{\alpha}_t$ 在最后的阶段几乎没有变化,反应在图像上的变化可参考图N25.2。
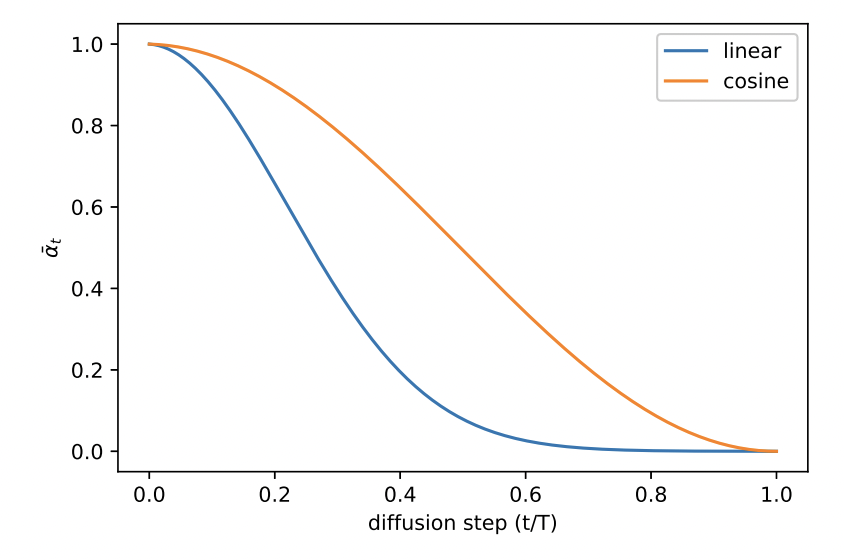
图 N25.1: 线性变换与余弦变换下对应的 $\bar{\alpha}_t$ 的变化。

图 N25.2: 线性变换(上)与余弦变化下对应的含噪图片的变化情况。
这种突变导致很多扩散步数实际上是无效的,为了缓解这一点,作者直接针对 $\bar{\alpha}_t$ 进行建模,令
\[\bar{\alpha}_t=\frac{f(t)}{f(0)}, \quad f(t)=\cos \left(\frac{t / T+s}{1+s} \cdot \frac{\pi}{2}\right)^2 \tag{N.1}\]余弦变换的特点在于,在中间区段, $\bar{\alpha}_t$ 趋向于线性变化,而在 $t=0$ 和 $t=T$ 附件,$\bar{\alpha}_t$ 的变化十分缓慢。关于上式中其他参数的选择,可以参考原文相关章节。根据 diffuser 库的代码,具体的实现为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def betas_for_alpha_bar(
num_diffusion_timesteps,
max_beta=0.999,
alpha_transform_type="cosine",
):
"""
Create a beta schedule that discretizes the given alpha_t_bar function, which defines the cumulative product of
(1-beta) over time from t = [0,1].
Contains a function alpha_bar that takes an argument t and transforms it to the cumulative product of (1-beta) up
to that part of the diffusion process.
Args:
num_diffusion_timesteps (`int`): the number of betas to produce.
max_beta (`float`): the maximum beta to use; use values lower than 1 to
prevent singularities.
alpha_transform_type (`str`, *optional*, default to `cosine`): the type of noise schedule for alpha_bar.
Choose from `cosine` or `exp`
Returns:
betas (`np.ndarray`): the betas used by the scheduler to step the model outputs
"""
if alpha_transform_type == "cosine":
def alpha_bar_fn(t):
return math.cos((t + 0.008) / 1.008 * math.pi / 2) ** 2
elif alpha_transform_type == "exp":
def alpha_bar_fn(t):
return math.exp(t * -12.0)
else:
raise ValueError(f"Unsupported alpha_tranform_type: {alpha_transform_type}")
betas = []
for i in range(num_diffusion_timesteps):
t1 = i / num_diffusion_timesteps
t2 = (i + 1) / num_diffusion_timesteps
betas.append(min(1 - alpha_bar_fn(t2) / alpha_bar_fn(t1), max_beta))
return torch.tensor(betas, dtype=torch.float32)
25.2.2 解码器(逆向生成)
在逆向过程中,我们希望反转正向的扩散过程。如果我们提前知道输入 $\boldsymbol{x}_0$,我们可以推导出单步正向过程对应的逆向过程9:
\[\begin{align} q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) & =\mathcal{N}\left(\boldsymbol{x}_{t-1} \mid \tilde{\mu}_t\left(\boldsymbol{x}_t, \boldsymbol{x}_0\right), \tilde{\beta}_t \mathbf{I}\right) \tag{25.6} \\ \tilde{\mu}_t\left(\boldsymbol{x}_t, \boldsymbol{x}_0\right) & =\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \boldsymbol{x}_0+\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \boldsymbol{x}_t \tag{25.7} \\ \tilde{\beta}_t & =\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t \tag{25.8} \end{align}\]当然,在生成一个新的数据时,我们并不知道 $\boldsymbol{x}_0$,但我们可以训练生成器来近似上述分布在 $\boldsymbol{x}_0$ 上的平均结果。因此,我们选择的生成器具有以下形式:
\[p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)=\mathcal{N}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right), \boldsymbol{\Sigma}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right) \tag{25.9}\]通常我们令 $\boldsymbol{\Sigma}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)=\sigma_t^2 \mathbf{I}$(译者注:即各向同性的对角协方差矩阵)。我们将在 25.2.4 节讨论如何学习 $\sigma_t^2$,但两种容易想到的选择是令 $\sigma_t^2=\beta_t$ 和 $\sigma_t^2=\tilde{\beta}_t$,两种选择分别对应于在[HJA20]6中介绍的反向过程熵的上限和下限。
在生成过程中产生的所有隐变量服从的联合概率分布为 \(p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{0: T}\right)= p\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\) ,其中我们令 $p\left(\boldsymbol{x}_T\right)=\mathcal{N}(\mathbf{0}, \mathbf{I})$。根据算法25.2提供的伪代码,我们可以从分布中采样得到新的样本。
25.2.3 模型拟合
我们将通过最大化证据下确界(evidence lower bound,ELBO)来拟合模型,类似于我们训练VAE的方式(第21.2节)。具体而言,对于每个数据样本 $\boldsymbol{x}_0$,我们有
\[\begin{align} \log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0\right) & =\log \left[\int d \boldsymbol{x}_{1: T} q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right) \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{0: T}\right)}{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\right] \tag{25.10}\\ & \geq \int d \boldsymbol{x}_{1: T} q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right) \log \left(p\left(\boldsymbol{x}_T\right) \prod_{t=1}^T \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)}\right) \tag{25.11}\\ & =\mathbb{E}_q\left[\log p\left(\boldsymbol{x}_T\right)+\sum_{t=1}^T \log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)}\right] \triangleq \text { Ł }\left(x_0\right) \tag{25.12} \end{align}\]我们现在讨论如何计算ELBO中的各个分项。基于马尔可夫属性,我们有 \(q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)=q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right)\),
同时根据贝叶斯定理,我们有
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right)=\frac{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)} \tag{25.13}\]将公式(25.13)代入ELBO中,我们有
\[\mathrm{L}\left(\boldsymbol{x}_0\right)=\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\bigg[\log p\left(\boldsymbol{x}_T\right)+\sum_{t=2}^T \log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)}+\underbrace{\sum_{t=2}^T \log \frac{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}}_*+\log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}\bigg] \tag{25.14}\]标记为*的项是一个折叠求和,可以简化如下:
\[\begin{align} * & =\log q\left(\boldsymbol{x}_{T-1} \mid \boldsymbol{x}_0\right)+\cdots+\log q\left(\boldsymbol{x}_2 \mid \boldsymbol{x}_0\right)+\log q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right) \tag{25.15}\\ & -\log q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)-\log q\left(\boldsymbol{x}_{T-1} \mid \boldsymbol{x}_0\right)-\cdots-\log q\left(\boldsymbol{x}_2 \mid \boldsymbol{x}_0\right) \tag{25.16}\\ & =-\log q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)+\log q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right) \tag{25.17} \end{align}\]所以负ELBO(变分上确界)定义为:
\[\begin{align} \mathcal{L}\left(\boldsymbol{x}_0\right) & =-\mathbb{E}_{q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)}\left[\log \frac{p\left(\boldsymbol{x}_T\right)}{q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right)}+\sum_{t=2}^T \log \frac{p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)}{q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)}+\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right] \tag{25.18} \\ & =\underbrace{D_{\mathbb{K L}}\left(q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \| p\left(\boldsymbol{x}_T\right)\right)}_{L_T\left(\boldsymbol{x}_0\right)} \tag{25.19}\\ & +\sum_{t=2}^T \mathbb{E}_{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)} \underbrace{D_{\mathbb{K L}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\right)}_{L_{t-1}\left(\boldsymbol{x}_0\right)}-\underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)} \log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)}_{L_0\left(\boldsymbol{x}_0\right)} \tag{25.20} \end{align}\]这些 $\textrm{KL}$ 项中每一项都存在解析解,因为所有的分布都是高斯分布。接下来我们将聚焦在 $L_{t-1}$ 项。考虑到 $\boldsymbol{x}_t=\sqrt{\overline{\alpha_t}} \boldsymbol{x}_0+\sqrt{\left(1-\bar{\alpha}_t\right)} \boldsymbol{\epsilon}$,式(25.7)可以写成:
\[\tilde{\mu}_t\left(\boldsymbol{x}_t, \boldsymbol{x}_0\right)=\frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}\right) \tag{25.21}\]因此,除了训练模型直接根据含噪输入 \(\boldsymbol{x}_t\) 预测去噪后的 $\boldsymbol{x}_{t-1}$ 的均值,我们也可以训练模型来直接预测噪声,然后再根据下式计算均值:
\[\boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, \boldsymbol{x}_0\right)=\frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right) \tag{25.22}\]基于上述的参数化形式,最终的损失函数将变成
\[L_{t-1}=\mathbb{E}_{\boldsymbol{x}_0 \sim q_0\left(\boldsymbol{x}_0\right), \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\bigg[\underbrace{\frac{\beta_t^2}{2 \sigma_t^2 \alpha_t\left(1-\bar{\alpha}_t\right)}}_{\lambda_t}\|\boldsymbol{\epsilon}-\epsilon_{\boldsymbol{\theta}}(\underbrace{\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}}_{\boldsymbol{x}_t}, t)\|^2\bigg] \tag{25.23}\]与时间相关的权重 $\lambda_t$ 确保训练目标对应于最大似然估计(假设变分确界是紧凑的)。然而,经验表明,如果我们设置 $\lambda_t=1$,模型输出的样本看起来更好。由此产生的简化版本的损失(在整个优化目标中同时需要考虑时间点 $t$ )由以下公式给出:
\[L_{\text {simple }}=\mathbb{E}_{\boldsymbol{x}_0 \sim q_0\left(\boldsymbol{x}_0\right), \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), t \sim \operatorname{Unif}(1, T)}\bigg[\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\underbrace{\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}}_{\boldsymbol{x}_t}, t)\|^2\bigg] \tag{25.24}\]整体训练过程展示在算法25.1中。我们可以使用更先进的加权方案来提高样本的感知质量,这在[Cho+22]10中讨论过。相反,如果目标是提高似然分数,我们可以同时优化噪声时间表,如第25.2.4节所讨论的。
模型训练完成后,我们可以使用始祖抽样(ancestral sampling)来生成数据,如算法25.2所示。


| 译者注(Kimi读文) |
文章《Perception Prioritized Training of Diffusion Models》的主要贡献点如下:
- 新的训练目标权重方案:文章提出了一种名为感知优先(Perception Prioritized, P2)的权重方案,用于优化扩散模型的训练目标。这种方案通过重新设计损失函数的权重分配,使得模型在训练过程中更加关注于学习感知上重要的特征。
- 深入分析模型学习过程:作者首先对扩散模型在不同噪声级别下的学习内容进行了深入的分析。他们发现,模型在噪声较小的级别上学习到的是不易察觉的细节,而在噪声较大的级别上学习到的是感知上显著的内容。基于这些观察,文章提出了P2权重方案,旨在优先训练模型学习感知上丰富的内容。
- 跨数据集、架构和采样策略的一致性能提升:通过在多个数据集上进行实验,文章展示了使用P2权重方案训练的扩散模型在性能上的显著提升。这些数据集包括CelebAHQ、Oxford-flowers和FFHQ等,证明了该方法的泛化能力和有效性。
- 与现有技术的比较:文章将使用P2权重方案的扩散模型与其他类型的生成模型进行了比较,包括生成对抗网络(GANs)和其他扩散模型。结果显示,P2权重方案在多个数据集上都取得了最先进的性能。
- 模型配置和采样步骤的鲁棒性分析:作者还探讨了P2权重方案在不同模型配置和采样步骤下的有效性。实验结果表明,无论模型配置如何变化,P2权重方案都能一致地提高模型的性能。
- 实现细节的提供:文章提供了关于所提出方法的实现细节,包括模型架构、超参数设置和训练过程的具体信息,这有助于其他研究者复现和进一步研究该方法。
总体而言,这篇文章通过提出一种新的训练目标权重方案,不仅提高了扩散模型的性能,还为理解和改进这类模型的学习过程提供了新的视角。
25.2.4 学习噪声时间表
在本节中,我们将介绍一种方法,该方法可以同时优化在编码器中所使用的噪声时间表,以实现最大化ELBO;这种方法被称为变分扩散模型(variational diffusion model, VDM) [Kin+21]7(译者注:默认的扩散模型在编码器中不存在可学习参数,而VDM在编码器中存在可学习参数)。
我们将使用如下的参数化方式来实现编码器:
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\mathcal{N}\left(\boldsymbol{x}_t \mid \hat{\alpha}_t \boldsymbol{x}_0, \hat{\sigma}_t^2 \mathbf{I}\right) \tag{25.25}\](需要注意的是此处的$\hat{\alpha}_t$,$\hat{\sigma}_t$ 与25.2.1节中的参数 $\alpha_t$,$\sigma_t$ 是不同的)。我们将学习预测两个参数的比率,而不是分别处理 $\hat{\alpha}_t$ 和 $\hat{\alpha}_t^2$,这个比率被称为信噪比(signal to noise ratio,SNR):
\[R(t)=\hat{\alpha}_t^2 / \hat{\sigma}_t^2 \tag{25.26}\]上式需要随着 $t$ 的增加而单调递减。这一点可以通过定义 \(R(t)=\exp \left(-\gamma_\phi(t)\right)\) 来实现,其中\(\gamma_\phi(t)\) 是一个单调神经网络。我们通常令 \(\hat{\alpha}_t=\sqrt{1-\sigma_t^2}\),这对应于25.4节讨论的variance preserving SDE。
沿用25.2.3节的推导,负ELBO(变分上确界)可以写成:
\[\mathcal{L}\left(\boldsymbol{x}_0\right)=\underbrace{D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \| p\left(\boldsymbol{x}_T\right)\right)}_{\text {prior loss }}+\underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)}\left[-\log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right)\right]}_{\text {reconstruction loss }}+\underbrace{\mathcal{L}_D\left(\boldsymbol{x}_0\right)}_{\text {diffusion loss }} \tag{25.27}\]其中前两项类似于标准VAE中出现的情况,最后的扩散损失为11:
\[\mathcal{L}_D\left(\boldsymbol{x}_0\right)=\frac{1}{2} \mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})} \int_0^1 R^{\prime}(t)\left\|\boldsymbol{x}_0-\hat{\boldsymbol{x}}_{\boldsymbol{\theta}}\left(z_t, t\right)\right\|_2^2 d t \tag{25.28}\]其中 $R^{\prime}(t)$ 是 SNR 函数的导数,\(\boldsymbol{z}_t=\alpha_t \boldsymbol{x}_0+\sigma_t \boldsymbol{\epsilon}_t\)。(具体推导参考[Kin+21]7)。
由于信噪比(SNR)函数是可逆的——因为单调性假设,我们可以进行变量替换,并且使一切变量都成为关于 \(v=R(t)\) 的函数而不是 $t$ 的函数。具体而言,令 \(\boldsymbol{z}_v=\alpha_v \boldsymbol{x}_0+\sigma_v \boldsymbol{\epsilon}\),以及 \(\tilde{\boldsymbol{x}}_{\boldsymbol{\theta}}(\boldsymbol{z}, v)=\hat{\boldsymbol{x}}_{\boldsymbol{\theta}}\left(\boldsymbol{z}, R^{-1}(v)\right)\)。则公式(25.28)可以重写成
\[\mathcal{L}_D\left(\boldsymbol{x}_0\right)=\frac{1}{2} \mathbb{E}_{\boldsymbol{\epsilon} \sim \mathcal{N}(\boldsymbol{0}, \mathbf{I})} \int_{R_{\min }}^{R_{\max }}\left\|\boldsymbol{x}_0-\tilde{\boldsymbol{x}}_{\boldsymbol{\theta}}\left(z_v, v\right)\right\|_2^2 d v \tag{25.29}\]其中 \(R_{\min }=R(1)\),\(R_{\max }=R(0)\)。所以我们发现SNR时间表的形状(即中间状态值)对结果没有影响,只有2个端点起作用。
等式(25.29)中的积分可以通过随机均匀采样时间点来估计。当处理 \(k\) 个样例的小批量训练数据时,我们可以使用低偏差采样器(low-discrepancy sampler,参见,第11.6.5节)来产生一个变分确界的低方差估计。在这种方法中,我们不是独立地对时间点进行抽样,而是抽样一个均匀随机数 \(u_0 \sim \operatorname{Unif}(0,1)\),然后将第 \(i\) 个样本的时间 \(t\) 设置为 \(t^i=\bmod \left(u_0+i / k, 1\right)\)。我们也可以对噪声时间表本身进行优化,以减少扩散损失的方差。
| 译者注(Kimi读文) |
这篇论文介绍了一类基于变分扩散模型(Variational Diffusion Models,简称VDMs,https://arxiv.org/pdf/2107.00630.pdf)的生成模型,并展示了它们在标准图像密度估计基准测试中的优异性能。以下是该论文的主要贡献点:
新的生成模型家族:作者提出了一种基于扩散的生成模型,这些模型在标准图像数据集(如CIFAR-10和ImageNet)上取得了最先进的对数似然(log-likelihood)结果。这些模型通过结合傅里叶特征(Fourier features)和可学习的扩散过程规范,实现了对图像的高质量生成。
理论理解的提高:通过对变分下界(Variational Lower Bound,简称VLB)的分析,作者提高了我们对使用扩散模型进行密度建模的理论理解。他们发现VLB可以简化为一个关于扩散数据信噪比的简短表达式,并通过这一发现证明了文献中提出的几个模型之间的等价性。
连续时间VLB的不变性:作者证明了在连续时间设置下,VLB对于噪声计划是不变的,除了信噪比在其端点的值。这使得他们能够学习一个最小化VLB估计器方差的噪声计划,从而加快了优化过程。
架构改进:结合上述理论进展和架构改进,VDMs在图像密度估计基准测试中取得了最先进的似然结果,超越了长期以来在这些基准测试中占主导地位的自回归模型,并且通常具有更快的优化速度。
无损压缩应用:作者展示了如何将模型作为无损压缩方案的一部分,并展示了接近理论最优的无损压缩率。
代码可用性:为了促进研究和应用,作者提供了模型的代码实现,可以在GitHub上找到。
这篇论文的贡献在于它不仅提出了一种新的生成模型,而且还通过理论分析和实验验证,展示了这种模型在图像生成和无损压缩等任务中的有效性和优越性。
25.2.5 案例:图像生成
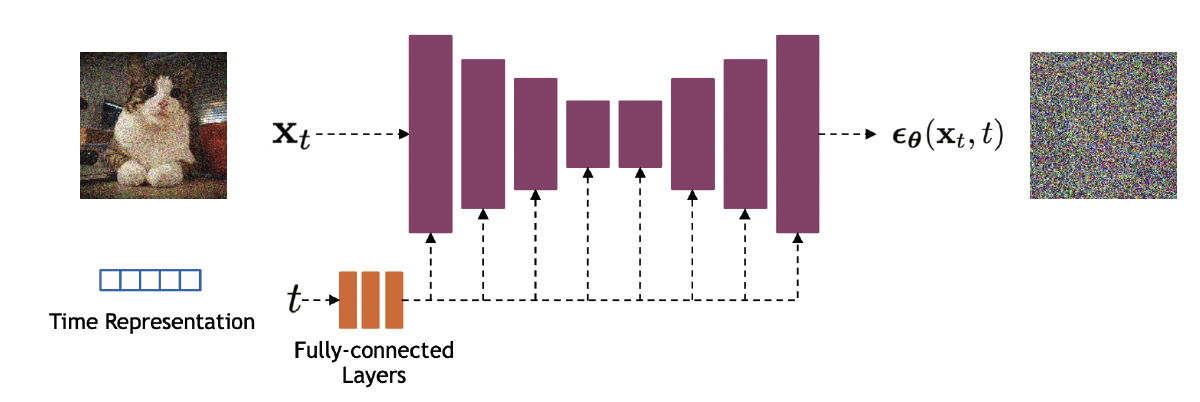
图25.3:降噪过程中U-net的结构示意图。图片引用自 [KGV22]1 的第26页。经Arash Vahdat允许后使用。
扩散模型经常被用来生成图像。图像生成最常用的结构基于U-net模型[RFB15]12,如图25.3所示。时间节点 $t$ 被编码为一个向量,使用的是正弦位置编码或随机傅里叶特征,随后被输入到残差模块,使用简单的空间加法或通过对组归一化层进行条件化[DN21a]13。当然,除了U-net之外,还有其他的架构。例如,最近的研究[PX22]14; [Li+22]15; [Bao+22a]16提出使用transformer来取代卷积层和反卷积层。
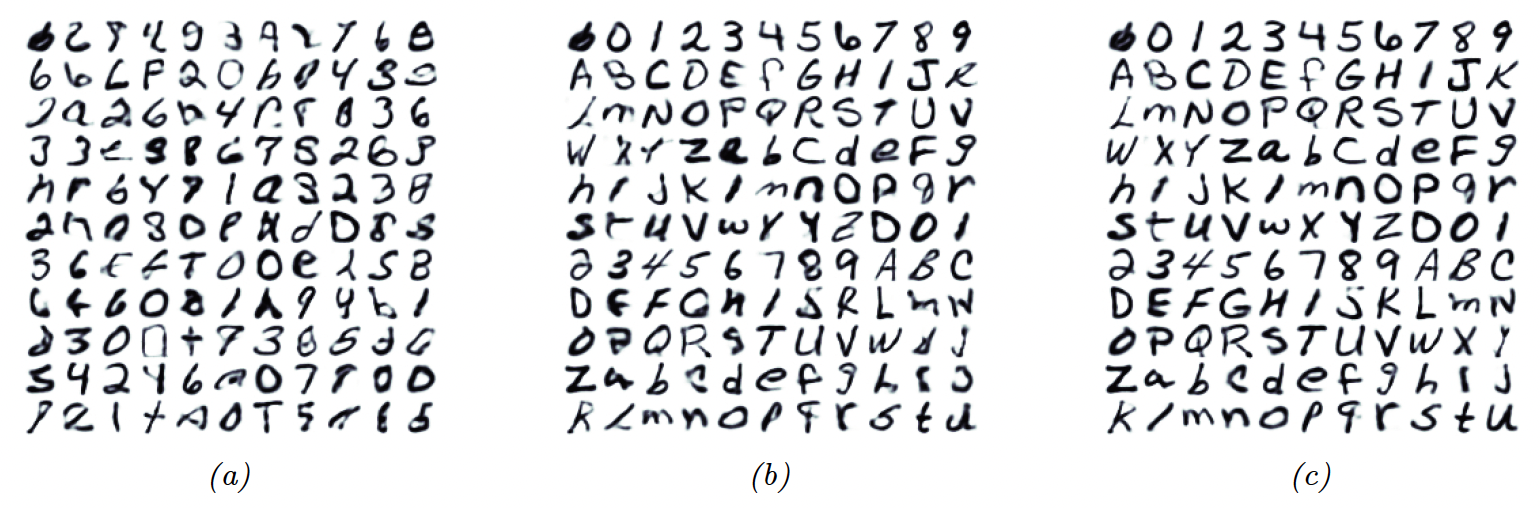
图25.4:一些由在 K40 GPU 上训练了大约 30 分钟的小型变分扩散模型生成的样本图像,这些模型是在 EMNIST 数据集上训练的。 (a) 无条件采样。 (b) 基于类别标签的条件采样。 (c) 使用无分类器引导(参见第 25.6.3 节)。由 diffusion_emnist.ipynb 生成。经 Alex Alemi 的友好授权使用。
图25.4展示了在EMNIST图像数据集上训练一个小型U-net VDM的结果。通过在大量数据(数百万图像)上长时间(数天)训练大规模参数(数十亿),扩散模型可以生成非常高质量的图像(见图20.2)。通过使用条件扩散模型,可以进一步提高结果,其中的条件信息提供了关于生成哪些类型图像的指导(见第25.6节)。
| 译者注(位置编码如何计算) |
在 transformer 的原文中,位置编码的计算方式为:
对于序列中的第 $k$ 个 token, 其位置编码的目标维度为 $d_{model}$, 每个维度 $i$ 的数值计算方式为:
$d(k,2i) = sin\bigg(\frac{k}{\frac{2i}{n^{d_{model}}}}\bigg)$
$d(k,2i+1) = cos\bigg(\frac{k}{\frac{2i}{n^{d_{model}}}}\bigg)$
在 pytorch 中,我们需要对上式进行一些变形,方便批量计算:
$\frac{1}{n^{\frac{2 i}{d_{\text {model }}}}}=n^{-\frac{2 i}{d_{\text {model }}}}=e^{\log \left(n^{\left.-\frac{2 i}{d_{\text {model }}}\right)}\right.}=e^{-\frac{2 i}{d_{\text {model }}} \log (n)}=e^{-\frac{2 i \log (n)}{d_{\text {model }}}}$
所以被除项可以批量计算,注意被除项的数量为 $d_{model}/2$:
1
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(n) / d_model))
所以对于一个最大长度为 $\text{max_length}$ 的序列,所有位置的被除项可以定义为:
1
2
k = torch.arange(0, max_length).unsqueeze(1)
div_term = k*div_term
接下来我们初始化位置编码:
1
2
3
4
5
pe = torch.zeros(max_length, d_model)
# set the odd values (偶数列)
pe[:, 0::2] = torch.sin(k * div_term)
# set the even values (奇数列)
pe[:, 1::2] = torch.cos(k * div_term)
25.3 Score-based 生成模型(SGMs)
在第24.3节中,我们讨论了如何使用score matching来拟合能量模型(EBMs)。该方法通过调整EBM的参数,使得模型的评分函数(score function)\(\nabla_{\boldsymbol{x}} \log p_{\boldsymbol{\theta}}(\boldsymbol{x})\),匹配真实数据的评分函数 \(\nabla_{\boldsymbol{x}} \log p_{\mathcal{D}}(\boldsymbol{x})\)。一个替代先估计标量能量函数再计算其评分 的方法是直接学习一个评分函数,该方法被称为 score-based generative model(SGM)[SE19]17; [SE20b]18; [Son+21b]19。我们可以使用basic score matching(第24.3.1节)、sliced score matching(第24.3.3节)或 denoising score matching(第24.3.2节)来优化评分函数 \(s_{\boldsymbol{\theta}}(\boldsymbol{x})\)。我们将在下文中更详细地讨论这类模型。(关于与EBMs的比较,参见[SH21]20。)
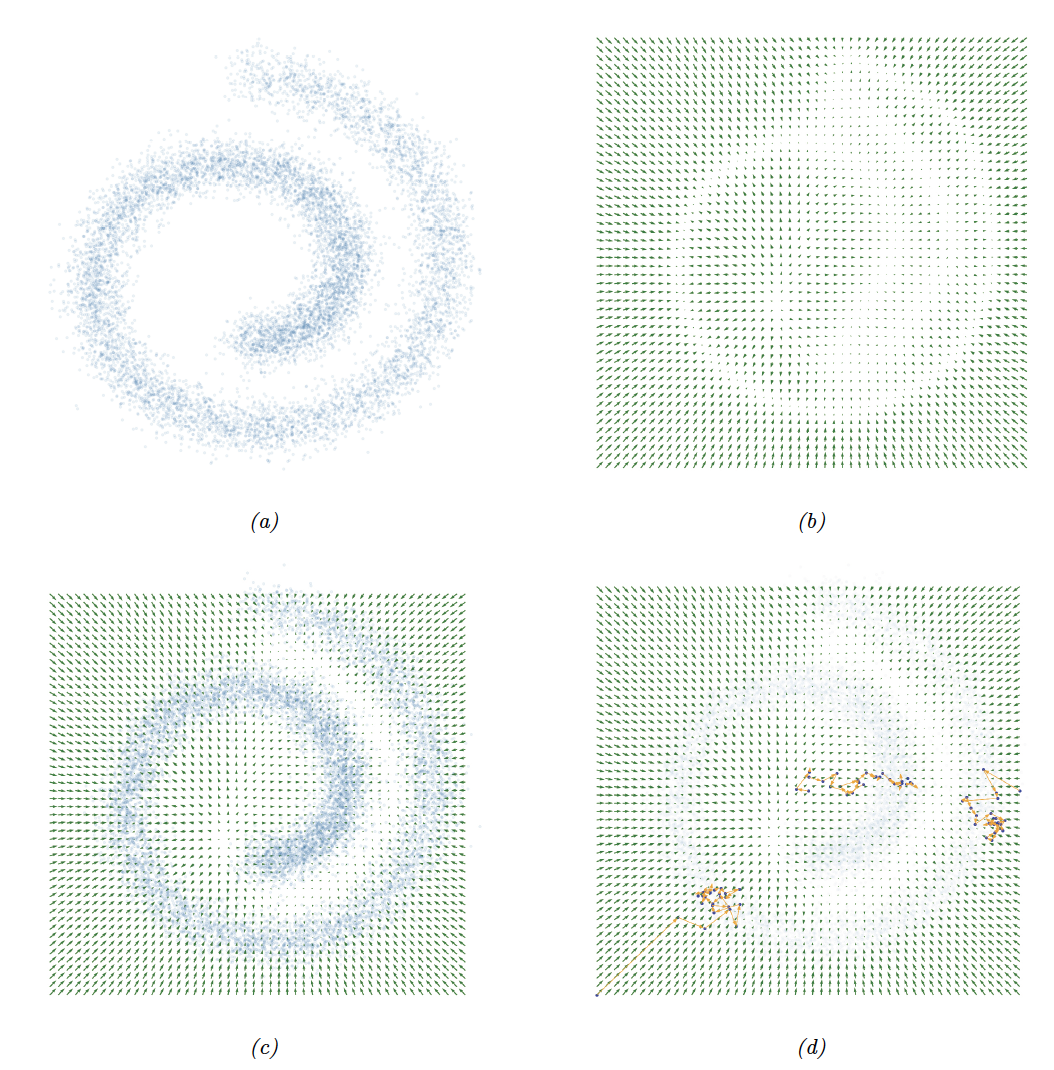
图25.5: 将SGM拟合到2D瑞士卷数据集。(a) 训练集。 (b) 使用score matching学习得分函数。(c) score function输出和经验密度的叠加。 (d) 应用于所学模型的朗之万采样。 我们展示了3条不同的轨迹,每条轨迹长度为25。由score_matching_swiss_roll.ipynb生成。
25.3.1 案例
在图25.5a中,我们可视化了瑞士卷数据集。我们使用basic score matching方法,拟合了一个具有2个隐层的MLP来估计评分函数,每层包含128个隐藏单元。在图25.5b中,我们展示了使用随机梯度下降(SGD)训练10000步后网络的输出结果。从中,我们没有发现主要的false negatives(因为数据密度最高的地方,对应的梯度场都是零),但存在一些 false positives(因为一些零梯度区域并不对应于高密度数据区域)。图25.5c中清晰地展示了经验数据的密度分布和模型的预测输出。在图25.5d中,我们展示了一些基于训练好的模型得到的采样结果,使用的是朗之万采样。
25.3.2 分层加噪
通常,当存在低密度数据区域时,score matching 可能会遇到困难。为了了解这一点,假设 $p_{\mathcal{D}}(\mathbf{x})=\pi p_0(\mathbf{x})+(1-\pi) p_1(\mathbf{x})$。令\(\mathcal{S}_0:=\left\{\mathbf{x} \mid p_0(\mathbf{x})>0\right\}\) 和
\(\mathcal{S}_1:=\left\{\mathbf{x} \mid p_1(\mathbf{x})>0\right\}\) 分别对应 \(p_0(\mathbf{x})\) 和 \(p_1(\mathbf{x})\) 的支撑集。当两个支撑集不相交时,$p_{\mathcal{D}}(\mathbf{x})$ 的score为:
\[\nabla_{\mathbf{x}} \log p_{\mathcal{D}}(\mathbf{x})= \begin{cases}\nabla_{\mathbf{x}} \log p_0(\mathbf{x}), & \mathbf{x} \in \mathcal{S}_0 \\ \nabla_{\mathbf{x}} \log p_1(\mathbf{x}), & \mathbf{x} \in \mathcal{S}_1\end{cases} \tag{25.30}\]这个score不依赖于权重$\pi$。因此,score matching不能正确地还原真实的分布。此外,朗之万采样在模式(mode)之间转换时也存在困难。(在实践中,即使不同模式的支撑集之间只存在大致的不相交,也会发生上述的情况。)
Song和Ermon [SE19]17; [SE20b]18以及Song等人[Son+21b]19通过使用不同强度的噪声扰动训练数据来克服这一困难。具体来说,他们使用以下的方法:
\[\begin{align} q_\sigma(\tilde{\boldsymbol{x}} \mid \boldsymbol{x}) & =\mathcal{N}\left(\tilde{\boldsymbol{x}} \mid \boldsymbol{x}, \sigma^2 \mathbf{I}\right) \tag{25.31}\\ q_\sigma(\tilde{\boldsymbol{x}}) & =\int p_{\mathcal{D}}(\boldsymbol{x}) q_\sigma(\tilde{\boldsymbol{x}} \mid \boldsymbol{x}) d \boldsymbol{x} \tag{25.32} \end{align}\]对于较强的噪声扰动,由于添加了噪声,不同模式的支撑集之间产生了连通,此时估算的权重是准确的。对于强度较小的噪声扰动,不同模式的支撑集不连通,但噪声扰动后的分布更接近原始未扰动的数据分布。使用诸如退火朗之万动力学[SE19]17; [SE20b]18; [Son+21b]19或扩散采样[SD+15a]21; [HJA20]6; [Son+21b]19等采样方法,我们可以首先从被最大噪声强度扰动后的分布中采样,然后平滑地减小噪声的强度,直到抵达最小噪声强度。这个过程有助于利用来自所有噪声强度层的信息,并在从弱噪声扰动分布中采样时保持强噪声扰动分布下获得的正确的权重估计。
在具体实现中,所有评分模型共享权重,并且用一个以噪声强度为条件的神经网络实现;这被称为噪声条件评分网络(noise conditional score network),形式为 \(\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{x}, \sigma)\) 。通过训练所有噪声强度下的score matching目标——每个噪声强度对应一个匹配目标——来估计不同强度下的评分函数。如果我们使用等式(24.33)中的denoising score matching目标,将得到:
\[\begin{align} \mathcal{L}(\boldsymbol{\theta} ; \sigma) & =\mathbb{E}_{q(\mathbf{x}, \tilde{\mathbf{x}})}\left[\frac{1}{2}\left\|\nabla_{\mathbf{x}} \log p_{\boldsymbol{\theta}}(\tilde{\mathbf{x}}, \sigma)-\nabla_{\mathbf{x}} \log q_\sigma(\tilde{\mathbf{x}} \mid \mathbf{x})\right\|_2^2\right] \tag{25.33} \\ & =\frac{1}{2} \mathbb{E}_{p_{\mathcal{D}}(\mathbf{x})} \mathbb{E}_{\tilde{\mathbf{x}} \sim \mathcal{N}\left(\boldsymbol{x}, \sigma^2 \mathbf{I}\right)}\left\{\left\|\boldsymbol{s}_{\boldsymbol{\theta}}(\tilde{\mathbf{x}}, \sigma)+\frac{(\tilde{\mathbf{x}}-\boldsymbol{x})}{\sigma^2}\right\|_2^2\right\} \tag{25.34} \end{align}\]其中我们使用了这样一个事实,即高斯分布的评分函数为:
\[\nabla_{\boldsymbol{x}} \log \mathcal{N}\left(\tilde{\boldsymbol{x}} \mid \boldsymbol{x}, \sigma^2 \mathbf{I}\right)=-\nabla_{\boldsymbol{x}} \frac{1}{2 \sigma^2}(\boldsymbol{x}-\tilde{\boldsymbol{x}})^{\top}(\boldsymbol{x}-\tilde{\boldsymbol{x}})=\frac{\boldsymbol{x}-\tilde{\boldsymbol{x}}}{\sigma^2} \tag{25.35}\]如果我们有 $T$ 个不同的噪声强度,我们可以使用加权的方式组合损失:
\[\mathcal{L}\left(\boldsymbol{\theta} ; \sigma_{1: T}\right)=\sum_{t=1}^T \lambda_t \mathcal{L}\left(\boldsymbol{\theta} ; \sigma_t\right) \tag{25.36}\]其中我们选择 \(\sigma_1>\sigma_2>\cdots>\sigma_T\) ,并且权重项满足 $ \lambda_t>0 $。
25.3.3 与 DDPM 的等价性
我们现在展示 score-based generative model 的训练目标与DDPM损失函数是等价的。为了验证这一点,首先使用 \(q_0\left(\boldsymbol{x}_0\right)\) 替换 \(p_{\mathcal{D}}(\boldsymbol{x})\),用 \(\boldsymbol{x}_t\) 替换 \(\tilde{\boldsymbol{x}}\) ,并用 \(\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\) 替换 \(\boldsymbol{s}_{\boldsymbol{\theta}}(\tilde{\boldsymbol{x}},\sigma)\)。我们还将使用随机地均匀采样一个时间点来计算等式(25.36)。那么等式(25.36)变成了以下形式:
\[\mathcal{L}=\mathbb{E}_{\boldsymbol{x}_0 \sim q_0\left(\boldsymbol{x}_0\right), \boldsymbol{x}_t \sim q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right), t \sim \operatorname{Unif}(1, T)}\left[\lambda_t\left\|\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)+\frac{\left(\boldsymbol{x}_t-\boldsymbol{x}_0\right)}{\sigma_t^2}\right\|_2^2\right] \tag{25.37}\]如果我们使用 \(\boldsymbol{x}_t=\boldsymbol{x}_0+\sigma_t \boldsymbol{\epsilon}\),并定义 \(\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)=-\frac{\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)}{\sigma_t}\),我们可以将其重写为
\[\mathcal{L}=\mathbb{E}_{\boldsymbol{x}_0 \sim q_0\left(\boldsymbol{x}_0\right), \boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), t \sim \operatorname{Unif}(1, T)}\left[\frac{\lambda_t}{\sigma_t^2}\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right\|_2^2\right] \tag{25.38}\]如果我们令 $\lambda_t=\sigma_t^2$,我们就可以得到等式(25.24)中的损失 $L_{\text{simple}}$。
25.4 使用微分方程建模连续时间模型
在这一部分,我们考虑某种极限情况下的DDPM模型——即 $T$ 趋向于无穷大,或者等效地,考虑无限多层噪声强度下的SGM模型。为了实现这一点,我们需要从离散的时间状态转换到连续的时间状态,这个过程使得相关的数学表达变得更加复杂。而因此带来的优势在于,我们可以利用已有的大量关于常微分方程以及随机微分方程(stochastic differential equations,SDE)求解器的知识,如我们所见,这可以实现生成速度的加快。
25.4.1 前向扩散随机微分方程
首先考虑前向扩散过程,$t$ 时刻的噪声强度 $\beta_t$ 被重写为 $\beta(t) \Delta t$,其中 $\Delta t$ 表示步长,此时 $t$ 时刻的含噪样本表示为:
\[\boldsymbol{x}_t=\sqrt{1-\beta_t} \boldsymbol{x}_{t-1}+\sqrt{\beta_t} \mathcal{N}(\mathbf{0}, \mathbf{I})=\sqrt{1-\beta(t) \Delta t} \boldsymbol{x}_{t-1}+\sqrt{\beta(t) \Delta t} \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{25.39}\]如果 $\Delta t$ 足够小,我们可以使用一阶泰勒级数展开来近似第一项,得到
\[\boldsymbol{x}_t \approx \boldsymbol{x}_{t-1}-\frac{\beta(t) \Delta t}{2} \boldsymbol{x}_{t-1}+\sqrt{\beta(t) \Delta t} \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{25.40}\]因此对于足够小的 $\Delta t$,我们有
\[\frac{\boldsymbol{x}_t-\boldsymbol{x}_{t-1}}{\Delta t} \approx-\frac{\beta(t)}{2} \boldsymbol{x}_{t-1}+\frac{\sqrt{\beta(t)}}{\sqrt{\Delta t}} \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{25.41}\]我们现在可以考虑连续时间(continuous time)下的极限情况,并将上式改写成如下随机微分方程(SDE):
\[\frac{d \boldsymbol{x}(t)}{d t}=-\frac{1}{2} \beta(t) \boldsymbol{x}(t)+\sqrt{\beta(t)} \frac{d \boldsymbol{w}(t)}{d t} \tag{25.42}\]其中 $\boldsymbol{w}(t)$ 代表标准维纳过程(Wiener process),也被称为布朗噪声(Brownian noise)。更一般地,我们可以使用Itô微积分表示法将此类SDEs写成如下形式(参见例如[SS19]22):
\[d \boldsymbol{x}=\underbrace{\boldsymbol{f}(\boldsymbol{x}, t)}_{\text {drift }} d t+\underbrace{g(t)}_{\text {diffusion }} d \boldsymbol{w} \tag{25.43}\]上述SDE中的第一项被称为漂移系数(drift coefficient),第二项被称为扩散系数(diffusion coefficient)。
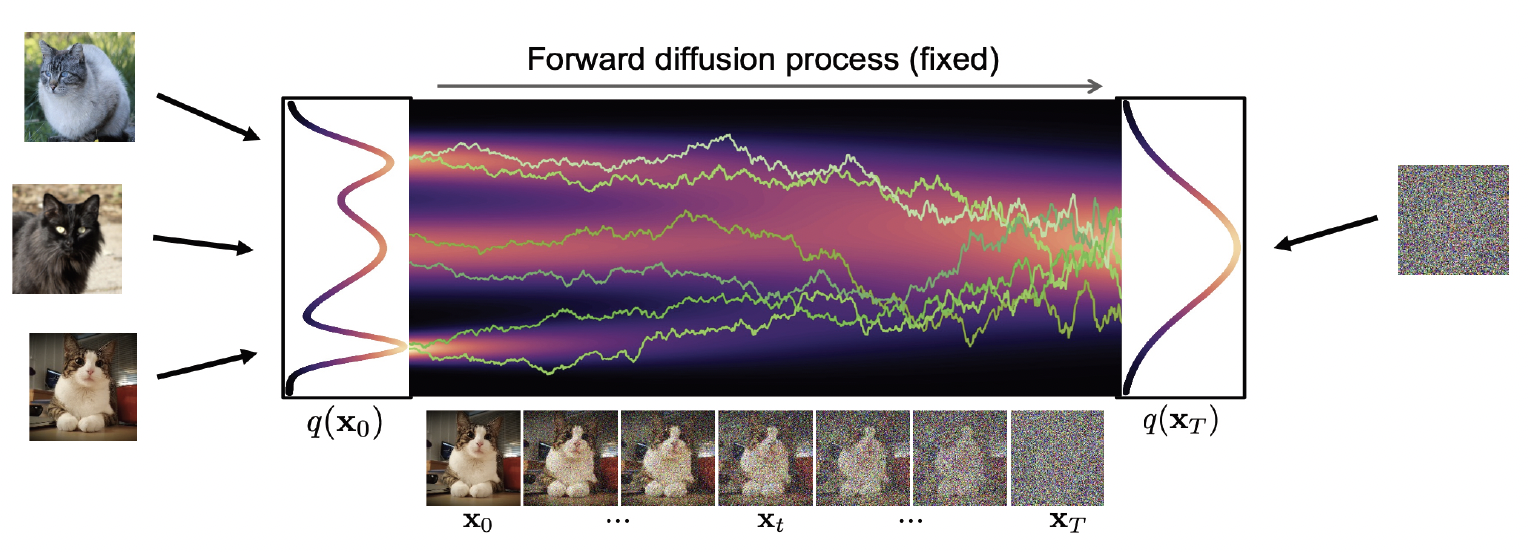
图25.6:连续时间下的前向扩散过程示意图。黄色曲线表示从SDE中得到的样本曲线。热力图表示使用概率流ODE得到的边际分布。图片引用自[KGV22]1 的第43页。经Karsten Kreis 许可后使用。
图25.6展示了一维空间中的数据是如何进行扩散的。我们可以通过如下的步骤绘制多条扩散路径:从数据分布中采样得到初始状态,然后使用欧拉-马鲁亚马(Euler-Maruyama)方法对时间进行积分:
\[\boldsymbol{x}(t+\Delta t)=\boldsymbol{x}(t)+\boldsymbol{f}(\boldsymbol{x}(t), t) \Delta t+g(t) \sqrt{\Delta t} \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{25.44}\]我们可以看到,$t=0$的左侧的数据分布是如何逐渐转变为$t=1$右侧的纯噪声分布的。
在[Son+21b]19中,他们展示了在 $T \rightarrow \infty$ 极限下DDPMs对应的SDE:
\[d \boldsymbol{x}=-\frac{1}{2} \beta(t) \boldsymbol{x} d t+\sqrt{\beta(t)} d \boldsymbol{\omega} \tag{25.45}\]其中 $\beta(t / T)=T \beta_t$。这里的漂移项与 $-\boldsymbol{x}$ 成正比,即鼓励最终的样本在扩散的过程中返回到0。因此,DDPM对应于一个方差保持(variance preserving)的过程。相比之下,SGMs对应的SDE表示为:
\[d \boldsymbol{x}=\sqrt{\frac{d\left[\sigma(t)^2\right]}{d t}} d \boldsymbol{\omega} \tag{25.46}\]其中 $\sigma(t / T)=\sigma_t$。此时的SDE的漂移项为0,所以对应于一个方差爆炸(variance exploding)的过程。
25.4.2 前向扩散常微分方程
我们可以不在每一步的扩散步骤中都添加高斯噪声,而是只对初始状态进行采样,然后根据下面的常微分方程(ODE)使样本随时间确定性 地进行演变:
\[d \boldsymbol{x}=\underbrace{\left[f(\boldsymbol{x}, t)-\frac{1}{2} g(t)^2 \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x})\right]}_{h(\boldsymbol{x}, t)} d t \tag{25.47}\]这被称为概率流常微分方程(probability flow ODE) [Son+21b]19, Sec D.3。我们可以使用任何一个ODE求解器计算任意时刻下的样本状态:
\[\boldsymbol{x}(t)=\boldsymbol{x}(0)+\int_0^t h(\boldsymbol{x}, \tau) d \tau \tag{25.48}\]图25.7b展示了样本轨迹的可视化效果。如果我们从不同的随机状态 $\boldsymbol{x}(0)$ 开始求解,那么产生的路径的边际分布将与SDE模型产生的边际分布相同。参见图25.6中的热图以获得说明。
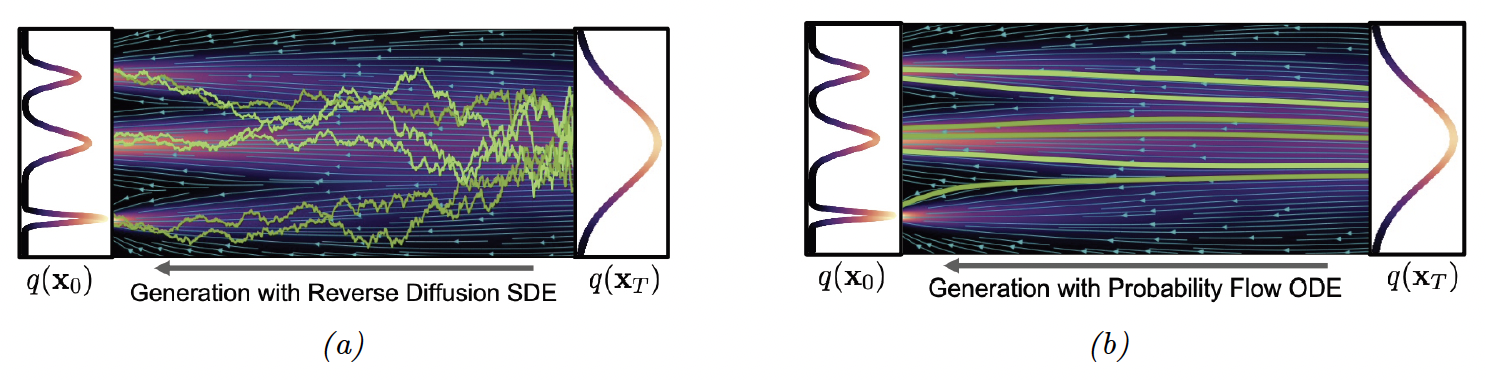
图25.7:逆扩散过程的示意图。(a)SDE的样本轨迹。(b)从概率流ODE中产生的确定的轨迹。图片引用自[KGV22]1 的第65页。经Karsten Kreis 许可后使用。
25.4.3 逆扩散随机微分方程
为了从SDE模型中生成样本,我们需要能够逆转SDE。[And82][^And82]中一个值得注意的结果表明,任何形式如方程(25.43)的正向SDE都可以被逆转,并获得如下的逆时SDE(reverse-time SDE):
\[d \boldsymbol{x}=\left[f(\boldsymbol{x}, t)-g(t)^2 \nabla_{\boldsymbol{x}} \log q_t(\boldsymbol{x})\right] d t+g(t) d \overline{\boldsymbol{w}} \tag{25.49}\]其中 $\overline{\boldsymbol{w}}$ 是当时间向后流动时的标准维纳过程,$dt$表示一个无穷小的负时间步长, $\nabla_{\boldsymbol{x}} \log q_t(\boldsymbol{x})$ 为前文介绍的评分函数。
在DDPM的设定下,逆时SDE具有以下形式:
\[d \boldsymbol{x}_t=\left[-\frac{1}{2} \beta(t) \boldsymbol{x}_t-\beta(t) \nabla_{\boldsymbol{x}_t} \log q_t\left(\boldsymbol{x}_t\right)\right] d t+\sqrt{\beta(t)} d \overline{\boldsymbol{w}}_t \tag{25.50}\]为了估计评分函数,正如我们在第25.3节中讨论的那样,我们可以使用denoising score matching,得到
\[\nabla_{\boldsymbol{x}_t} \log q_t\left(\boldsymbol{x}_t\right) \approx \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right) \tag{25.51}\](实际操作中,建议使用方差衰减技术,例如重要性采样,如[Son+21a][^Son21a]中所讨论的。)SDE变为
\[d \boldsymbol{x}_t=-\frac{1}{2} \beta(t)\left[\boldsymbol{x}_t+2 \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right] d t+\sqrt{\beta(t)} d \overline{\boldsymbol{w}}_t \tag{25.52}\]在拟合完评分函数后,我们可以使用始祖抽样(如第25.2节中所述)对其进行抽样,或者我们可以使用方程(25.44)中的欧拉-马鲁亚马积分方案,得到
\[\boldsymbol{x}_{t-1}=\boldsymbol{x}_t+\frac{1}{2} \beta(t)\left[\boldsymbol{x}_t+2 \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right] \Delta t+\sqrt{\beta(t) \Delta t} \mathcal{N}(\mathbf{0}, \mathbf{I}) \tag{25.53}\]参见图25.7a作为示例。
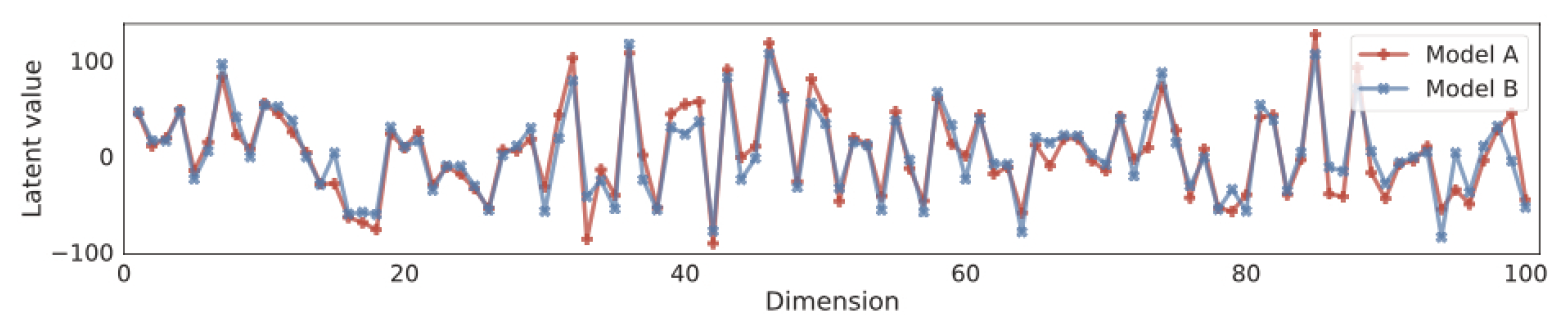
图25.8:对随机CIFAR-100图像获得的隐码前100维进行比较。 “模型A”和“模型B”分别使用不同的架构进行训练。来自[Son+21b]19的图7。 经YangSong的亲切许可使用。
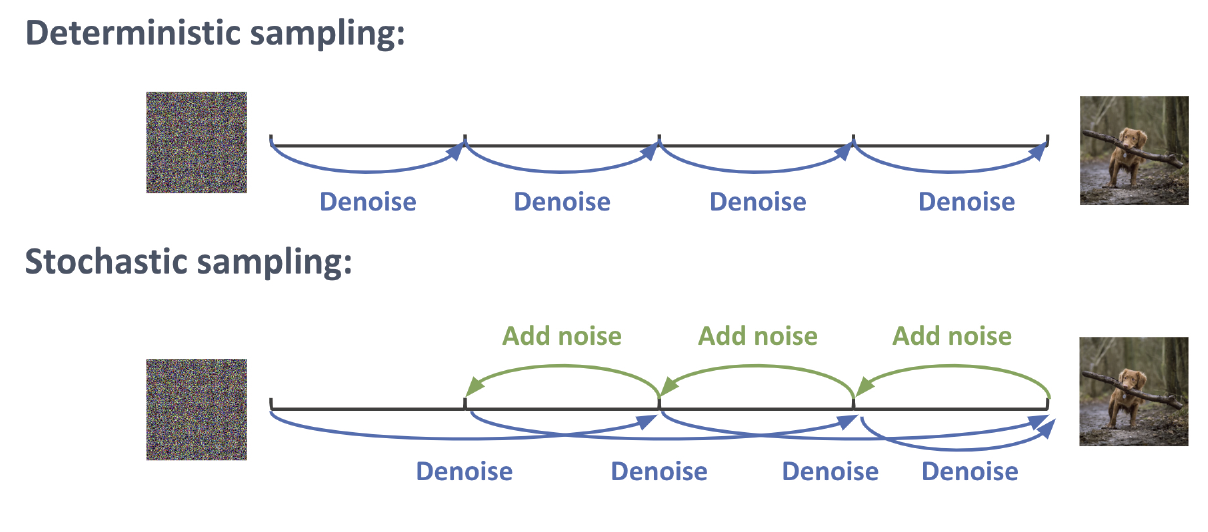
图25.9:利用4个步骤从逆向扩散过程中生成。(上图)确定性采样。 (下图)确定性和随机采样的混合。经过Ruiqi Gao的亲切许可使用。
25.4.4 逆扩散ODE
基于第25.4.2节中的结果,我们可以从方程(25.49)中的反向时间SDE推导出概率流ODE,得到
\[d \boldsymbol{x}_t=\left[f(\boldsymbol{x}, t)-\frac{1}{2} g(t)^2 \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right] d t \tag{25.54}\]如果我们像DDPM中那样设定 $f(\boldsymbol{x}, t)=-\frac{1}{2} \beta(t)$ 和 $g(t)=\sqrt{\beta(t)}$,这将变成
\[d \boldsymbol{x}_t=-\frac{1}{2} \beta(t)\left[\boldsymbol{x}_t+\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right] d t \tag{25.55}\]参见图25.7b作为示例。一种简单的求解此ODE的方法是使用欧拉方法
\[\boldsymbol{x}_{t-1}=\boldsymbol{x}_t+\frac{1}{2} \beta(t)\left[\boldsymbol{x}_t+\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right] \Delta t \tag{25.56}\]然而,在实践中,使用更高阶的ODE求解器,比如Heung方法[Kar+22][^Kar22],可以得到更好的结果。
该模型是神经ODE的一个特例,也称为连续归一化流(请参见第23.2.6节)。因此,我们可以推导出精确的边际对数似然。但是,我们没有直接最大化这个(这样做代价很大),而是使用 score matching 来拟合模型。
确定性ODE方法的另一个优点是它保证了生成模型是可辨别的。要理解这一点,请注意ODE(在前向和反向两个方向上)是确定性的,并且由评分函数唯一确定。如果架构足够灵活,并且有足够的数据,那么 score matching 将恢复出数据生成过程的真实评分函数。因此,在训练完成之后,给定的数据点将映射到潜在空间中的唯一点,无论模型架构或初始化如何(参见图25.8)。
此外,由于潜在空间中的每个点都解码为一个独特的图像,我们可以在潜在空间进行“语义插值”,以生成具有介于两个输入示例之间属性的图像(参见图20.9)。
25.4.5 SDE与ODE方法对比
在第25.4.3节中,我们将反向扩散过程描述为一个SDE,在25.4.4节中,我们将其描述为一个ODE。我们可以按照下面的方式重写方程(25.49)中的SDE,从而看到两种方法之间的联系:
\[d \boldsymbol{x}_t=\underbrace{-\frac{1}{2} \beta(t)\left[\boldsymbol{x}_t+\boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\right] d t}_{\text {probability flow ODE }} \underbrace{-\frac{1}{2} \beta(t) \boldsymbol{s}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right) d t+\sqrt{\beta(t)} d \overline{\boldsymbol{w}}_t}_{\text {Langevin diffusion SDE }} \tag{25.57}\]连续的噪声注入可以补偿ODE项数值积分引入的误差。因此,最终生成的样本通常看起来更好。然而,ODE方法可能更快。幸运的是,有可能结合这些技术,正如[Kar+22][^Kar22]中提出的那样。基本思想如图25.9所示:我们交替执行使用ODE求解器的确定性步骤,然后在结果中添加少量噪声。这可以重复进行一定次数。(我们将在第25.5节中讨论减少所需步骤数量的方法。)

图25.10:。
25.4.6 案例
Winnie Xu编写的一个简单的JAX实现上述想法可以在diffusion_mnist.ipynb中找到。这个实现使用 denoising score matching 在MNIST图像上拟合一个小型模型。然后它通过使用diffrax库求解概率流ODE从模型中生成样本。通过将这种方法扩展到更大的模型,并训练更长的时间,有可能产生非常令人印象深刻的结果,如图25.10所示。
25.5 加速扩散模型
扩散模型的主要缺点之一是生成样本的过程中需要迭代步骤,这可能会很慢。虽然可以只采取更少的、更大的步长,但结果会差很多。在这一节中,我们简要提及一些已经提出来解决这个重要问题的技术。在最近的综述论文[UAP22][^UAP22]; [Yan+22]2; [Cao+22]3中还提到了许多其他技术。
25.5.1 DDIM 采样
在这一节中,我们将描述[SME21][^SME21]中的去噪扩散隐式模型(denoising diffusion implicit model,DDIM),它可用于高效的确定性地样本生成。具体而言,DDIM的第一步是使用非马尔可夫前向扩散过程,所以它总是以输入样本本身以及前一步的样本为条件:
\[q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\bar{\alpha}_{t-1}} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_{t-1}-\tilde{\sigma}_t^2} \frac{\boldsymbol{x}_t-\sqrt{\bar{\alpha}_t}}{\sqrt{1-\bar{\alpha}_t}}, \tilde{\sigma}_t^2 \mathbf{I}\right) \tag{25.58}\]对应的反向过程是
\[p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)=\mathcal{N}\left(\sqrt{\bar{\alpha}_{t-1}} \hat{\boldsymbol{x}}_0+\sqrt{1-\bar{\alpha}_{t-1}-\tilde{\sigma}_t^2} \frac{\boldsymbol{x}_t-\sqrt{\bar{\alpha}_t} \hat{\boldsymbol{x}}_0}{\sqrt{1-\bar{\alpha}_t}}, \tilde{\sigma}_t^2 \mathbf{I}\right) \tag{25.59}\]其中 \(\hat{\boldsymbol{x}}_0=\hat{\boldsymbol{x}}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right)\) 是模型预测的输出。通过令 \(\tilde{\sigma}_t^2=0\),反向过程在给定初始先验样本(其方差由 \(\tilde{\sigma}_T^2\) 控制)的情况下变得完全确定。与第25.4.4节中讨论的方法相比,由此产生的概率流ODE在使用少量步骤时可以得到更好的结果。
请注意,该模型的加权负变分下确界(VLB)与第25.2节中的 $L_{\text{simple}}$ 相同,因此 DDIM 采样器可以应用于训练过的 DDPM 模型。
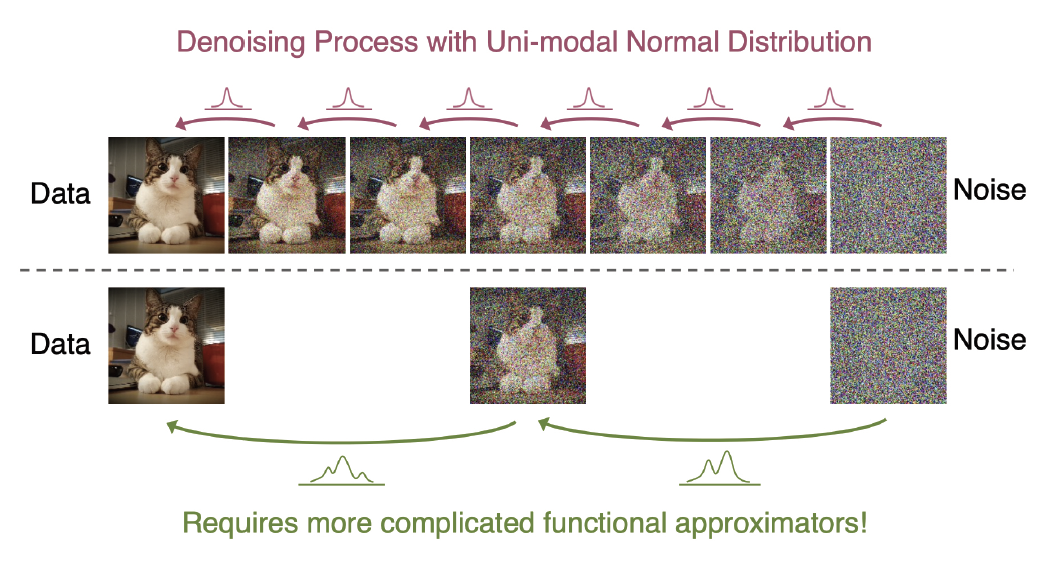
图25.11:。
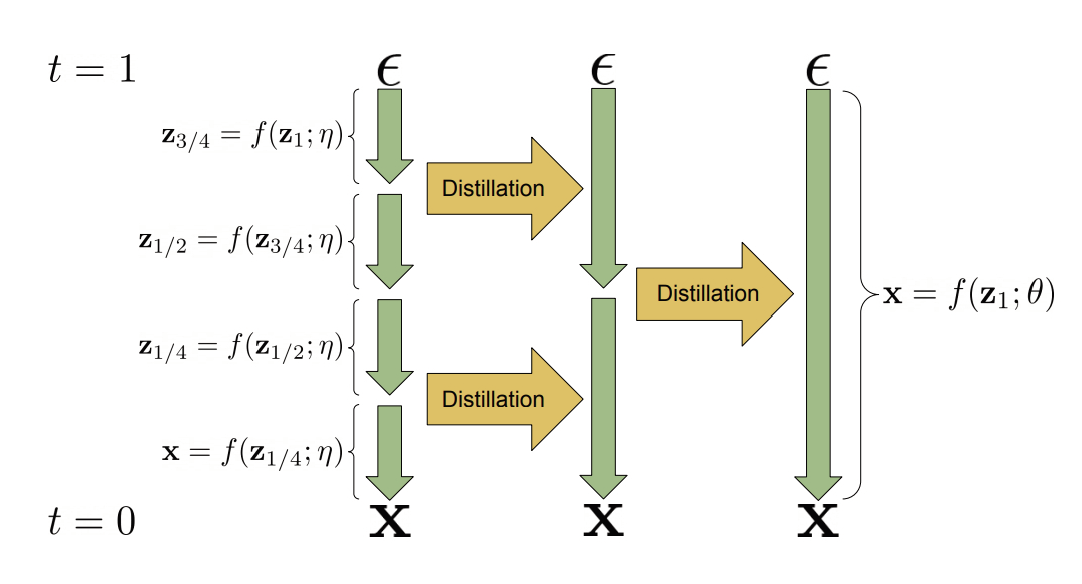
图25.12:。

25.5.2 非高斯解码器网络
如图25.11所示,如果反向过程采用更大的采样步长,则在给定含噪输入的情况下,清晰输出的诱导分布(induced distribution)将变得多峰值。这需要对分布 \(p_\boldsymbol{\theta}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)\) 使用更复杂的建模形式。在 [Gao+21]23 中,他们使用EBM来拟合这个分布。然而,这仍然需要使用MCMC(马尔科夫链蒙特卡罗)来抽取样本。在 [XKV22]24 中,他们使用GAN(生成对抗网络,第26章)来拟合这个分布。这使我们能够通过将高斯噪声传递给生成器来轻松地抽取样本。相比于单阶段生成对抗网络(GAN),其优势在于生成器和判别器都在解决一个更为简单的问题,这导致了更高的模态覆盖率和更好的训练稳定性。与标准扩散模型相比,我们可以用更少的步骤中生成高质量的样本。
25.5.3 蒸馏
在这一节中,我们讨论了[SH22]25的渐进式蒸馏方法,它提供了一种创建扩散模型的方法,该模型只需要少量步骤即可生成高质量的样本。基本思路如下:首先我们以通常的方式训练一个DDPM模型,并且使用DDIM方法从中采样;我们将其视为teacher模型。我们使用这个模型生成中间隐变量状态,并训练一个student模型来预测teacher模型每隔一步的输出,如图25.12所示。在student模型训练完成后,它可以生成与teacher模型一样好的结果,但步骤减半。然后,这个student可以教导新一代更快的student。具体的伪代码见算法25.4,应与标准训练过程的算法25.3进行比较。请注意,每一轮教学变得更快,因为teacher变得更小,因此执行蒸馏的总时间相对较短。最终的模型可以在短短4步内生成高质量样本。
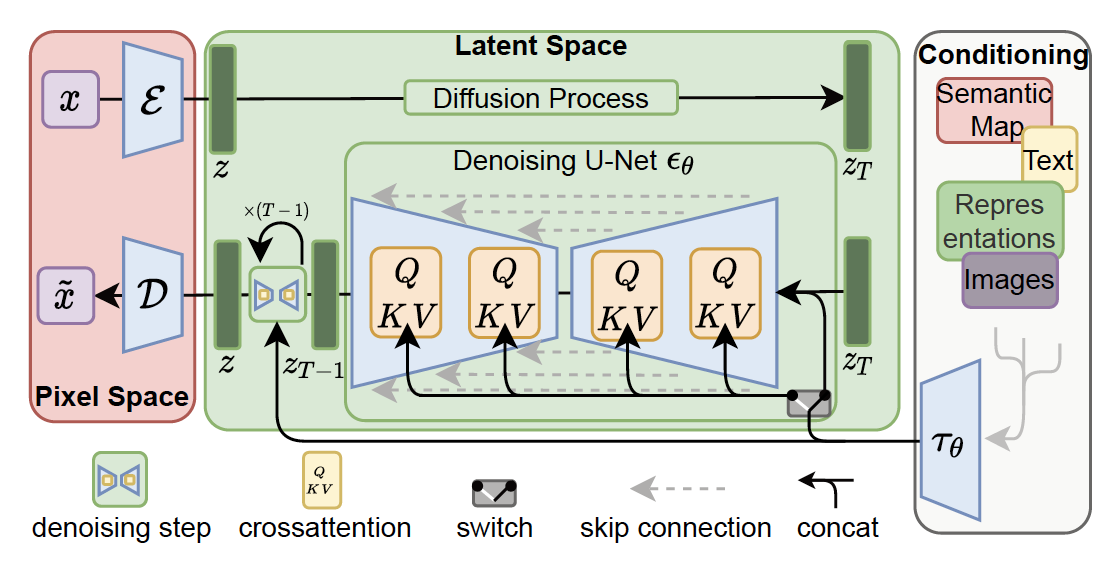
图25.13:。
25.5.4 隐空间扩散
加速图像扩散模型的另一种方法是首先将图像编码到一个低维隐空间中,然后在隐空间中拟合扩散模型。这个想法已经在几篇论文中被使用。
在[Rom+22][^Rom22]的潜在扩散模型(latent diffusion model,LDM)中,他们采用了一个双阶段训练方案,首先拟合了一个VAE(变分自动编码器),增加了一个感知损失,然后将扩散模型拟合到隐空间中。该架构如图25.13所示。LDM构成了Stability AI创建的非常受欢迎的stable diffusion的基础。在[VKK21][^VKK21]的 latent score-based generative model(LSGM)中,他们首先训练一个分层VAE,然后联合训练VAE和一个扩散模型。
除了速度之外,将扩散模型与VAE编码器相结合的另一个优点是,它使得将扩散应用于许多不同类型的数据变得简单,例如文本和图形:我们只需要定义一个合适的架构将输入域嵌入到一个连续的隐空间中。然而,请注意,也可以直接在离散状态空间内定义扩散,我们将在第25.7节中讨论。
到目前为止,我们讨论了在VAE之上应用扩散的方法。然而,我们也可以反过来,在DDPM模型之上拟合一个VAE,其中我们使用扩散模型来“后处理”来自VAE的模糊样本。有关细节,请参见[Pan+22][^Pan22]。
25.6 条件生成
在这一节中,我们将讨论如何从一个扩散模型中生成样本,其中我们将以一些边际信息 $\boldsymbol{c}$ 作为条件,比如一个类别标签或文本提示。
25.6.1 条件扩散模型
控制生成模型样本生成的最简单方式是在 $(\boldsymbol{c}, \boldsymbol{x})$ 对上训练它,以最大化条件似然 $p(\boldsymbol{x} \mid \boldsymbol{c})$ 。如果条件信号 $c$ 是一个标量(例如,一个类别标签),它可以被映射到一个嵌入向量,然后通过spatial addition 或使用它来调节group normalization层来整合到网络中。如果输入 $\boldsymbol{c}$ 是一张图片,我们可以简单地将其作为额外的通道与$\boldsymbol{x}_t$连接起来。如果输入$c$是文本提示,我们可以得到它的 embedding,然后使用 spatial addition 或交叉注意力(见图25.13 作为示例)。
25.6.2 Classifier guidance
条件扩散模型的一个问题是,我们需要对每种想要使用的条件进行重新训练。一种替代方法,被称为分类器引导(classifier guidance),该方法在[DN21b][^DN21b]中提出,它允许我们利用一个预训练的判别式分类器 $p(c|\boldsymbol{x})$ 来控制样本生成的过程。其思想如下。首先我们使用贝叶斯定理得到:
\[\log p(\boldsymbol{x} \mid \boldsymbol{c})=\log p(\boldsymbol{c} \mid \boldsymbol{x})+\log p(\boldsymbol{x})-\log p(\boldsymbol{c}) \tag{25.60}\]此时的评分函数变成
\[\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x} \mid \boldsymbol{c})=\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x})+\nabla_{\boldsymbol{x}} \log p(\boldsymbol{c} \mid \boldsymbol{x}) \tag{25.61}\]我们现在可以使用这个条件得分来生成样本,而不是无条件得分。我们可以进一步通过将其乘以一个大于1的因子$w$来增强条件信息的影响:
\[\nabla_{\boldsymbol{x}} \log p_w(\boldsymbol{x} \mid \boldsymbol{c})=\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x})+w \nabla_{\boldsymbol{x}} \log p(\boldsymbol{c} \mid \boldsymbol{x}) \tag{25.62}\]在实践中,可以通过从以下内容生成样本来实现这一点:
\[\boldsymbol{x}_{t-1} \sim \mathcal{N}(\boldsymbol{\mu}+w \boldsymbol{\Sigma} \boldsymbol{g}, \boldsymbol{\Sigma}), \boldsymbol{\mu}=\boldsymbol{\mu}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right), \boldsymbol{\Sigma}=\boldsymbol{\Sigma}_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t, t\right), \boldsymbol{g}=\nabla_{\boldsymbol{x}_t} \log p_{\boldsymbol{\phi}}\left(\boldsymbol{c} \mid \boldsymbol{x}_t\right) \tag{25.63}\]25.6.3 Classifier-free guidance
不幸的是,\(p\left(\boldsymbol{c} \mid \boldsymbol{x}_t\right)\) 是一个判别模型,该模型可能会忽视输入 $\boldsymbol{x}_t$ 中的许多细节。因此,沿着由 \(\nabla_{\boldsymbol{x}_t} \log p\left(\boldsymbol{c} \mid \boldsymbol{x}_t\right)\) 指定的方向更新样本可能会得到较差的结果,这类似于我们创建对抗性图像时发生的情况。此外,由于 $\boldsymbol{x}_t$ 在其模糊度上会有所不同,我们需要为每个时间步骤训练一个分类器。
在[HS21][^HS21]中,他们提出了一种称为无分类器引导(classifier-free guidance)的技术,该技术从生成模型中推导出分类器,使用 $p(\boldsymbol{c} \mid \boldsymbol{x})=\frac{p(\boldsymbol{x} \mid \boldsymbol{c}) p(\boldsymbol{c})}{p(\boldsymbol{x})}$ ,我们可以得到
\[\log p(\boldsymbol{c} \mid \boldsymbol{x})=\log p(\boldsymbol{x} \mid \boldsymbol{c})+\log p(\boldsymbol{c})-\log p(\boldsymbol{x}) \tag{25.64}\]这要求学习两个生成模型,即 $p(\boldsymbol{x} \mid \boldsymbol{c})$ 和 $p(\boldsymbol{x})$。然而,在实践中我们可以使用同一个模型,并简单地令 $c=\emptyset$ 来表示无条件的情况。然后我们使用这个隐式分类器来得到以下修改后的评分函数:
\[\begin{align} \nabla_{\boldsymbol{x}}[\log p(\boldsymbol{x} \mid \boldsymbol{c})+w \log p(\boldsymbol{c} \mid \boldsymbol{x})] & =\nabla_{\boldsymbol{x}}[\log p(\boldsymbol{x} \mid \boldsymbol{c})+w(\log p(\boldsymbol{x} \mid \boldsymbol{c})-\log p(\boldsymbol{x}))] \tag{25.65}\\ & =\nabla_{\boldsymbol{x}}[(1+w) \log p(\boldsymbol{x} \mid \boldsymbol{c})-w \log p(\boldsymbol{x})] \tag{25.66} \end{align}\]更大的权重 $w$ 通常会导致更好的单个样本质量,但多样性会变低。
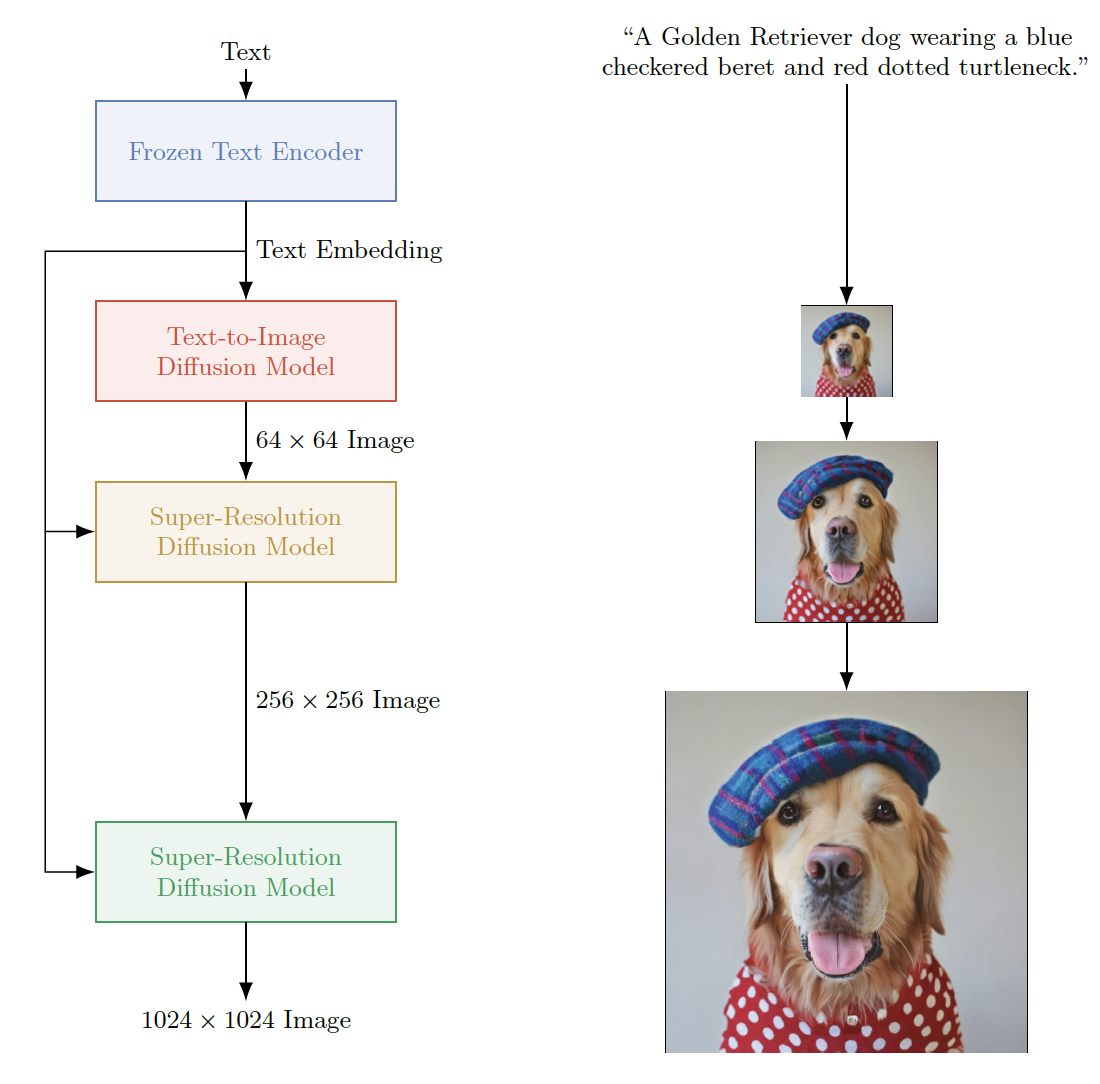
图25.14:。
25.6.4 生成高分辨图片
为了生成高分辨率图像,[Ho+21][^Ho21]提出使用级联生成(cascaded generation),首先训练一个模型来生成64x64像素的图像,然后训练一个单独的超分辨率模型(super-resolution model)将其映射到256x256或1024x1024像素。这种方法被用于谷歌的Imagen模型[Sah+22][^Sah22],这是一个文本到图像的系统(参见图25.14)。Imagen使用大型预训练文本编码器T5-XXL[Raf+20a][^Raf20a],结合基于U-net架构的VDM模型(第25.2.4节),生成引人注目的图像(参见图20.2)。
除了基于文本的条件外,也有可能基于另一幅图像进行条件设置,以创建图像到图像变换(image-to-image translation)的模型。例如,我们可以学习将灰度图像 $\boldsymbol{c}$ 映射到彩色图像 $\boldsymbol{x}$,或者将损坏或遮挡的图像 $\boldsymbol{c}$ 映射到干净的版本 $\boldsymbol{x}$ 。这可以通过训练多任务条件扩散模型来完成,如[Sah+21][^San21]中所解释的。参见图20.4一些示例输出。
25.7 离散隐空间内的扩散模型
截至目前,在本章中,我们主要关注用于生成实数域数据的高斯扩散模型。实际上,我们也可以定义用于离散数据的扩散模型,例如文本或语义分割的标签,这可以通过使用一个连续的潜在嵌入空间来实现(见第25.5.4节),或者直接在离散状态空间上定义扩散操作,我们将在下文讨论。
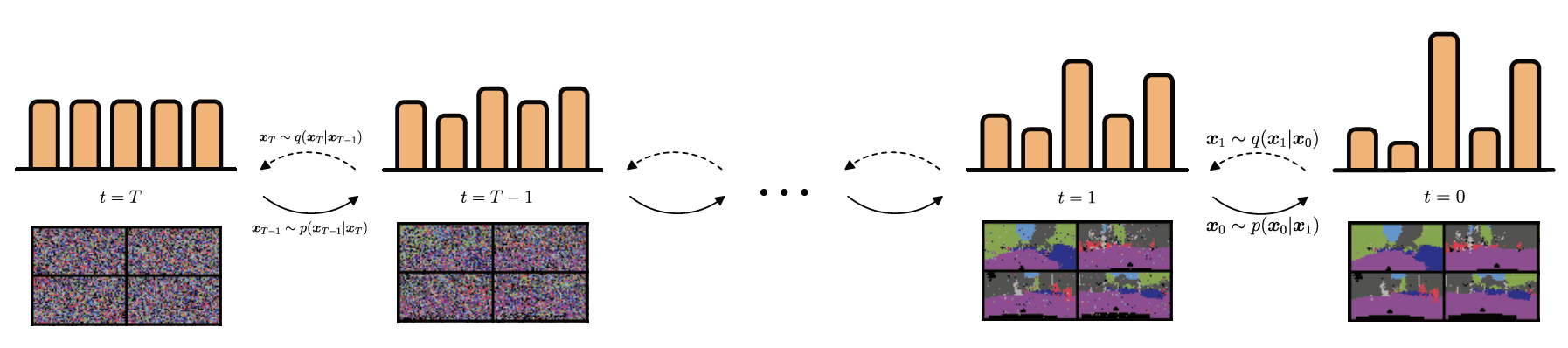
图25.15:。
25.7.1 离散降噪扩散概率模型
在本节中,我们讨论[Aus+21][^Aus21]中的离散去噪扩散概率模型(Discrete Denoising Diffusion Probabilistic Model,D3PM),它直接在离散状态空间定义了一个离散时间扩散过程。(这是基于先前的工作,如多项式扩散(multinomial diffusion)[Hoo+21][^Hoo21],以及原始扩散论文[SD+15b]5。)
如图25.15所示,我们在语义分割的设定下进行讨论,在当前设定中,类别标签与图像中的每个像素相关联。在图25.15的右侧,我们展示了一些示例图像,以及它们在单个像素上诱导的相应类别分布。我们使用下面描述的随机采样过程,逐渐将这些像素级别的类别分布转化为均匀分布。然后我们学习一个神经网络来反转这个过程,所以它可以从噪声生成离散数据,在图25.15中,这相当于从左向右移动的过程。
为了确保训练效率,我们要求可以有效地从分布 \(q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)\) 中采样任意时间 $t$ 对应的含噪样本,这样我们可以在优化变分确界(方程25.27)时随机采样时间步骤 $t$。此外,我们要求 \(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)\) 具有易于处理的形式,使得我们可以高效地计算KL项:
\[L_{t-1}\left(\boldsymbol{x}_0\right)=\mathbb{E}_{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)} D_{\mathbb{K} \mathbb{L}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\right) \tag{25.67}\]最后,如果前向过程收敛于一个已知的稳态分布 $\pi\left(\boldsymbol{x}_T\right)$,这将有助于我们用于选择先验分布 $p\left(\boldsymbol{x}_T\right)$从而确保 \(D_{\mathbb{K} \mathbb{L}}\left(q\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \| p\left(\boldsymbol{x}_T\right)\right)=0\)。
为了满足上述要求,我们假设每个时间点下的状态由 $D$ 个独立的分区组成,每个分区表示一个类别变量 $x_t \in{1, \ldots, K}$,我们用 one-hot 行向量 $\boldsymbol{x}_0$ 表示每个变量。一般来说,这将代表一个概率向量(译者注:概率向量是指向量的每个分量对应某个事件发生的概率)。然后我们定义前向扩散核如下:
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)=\operatorname{Cat}\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1} \mathbf{Q}_t\right) \tag{25.68}\]其中 \(\left[\mathbf{Q}_t\right]_{i j}=q\left(x_t=j \mid x_{t-1}=k\right)\) 是一个行随机转移矩阵。(我们在25.7.2节讨论如何定义 $\textbf{Q}_t$。)
我们可以通过以下步骤推导出前向过程中第 $t$ 步的边际分布:
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\operatorname{Cat}\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0 \overline{\mathbf{Q}}_t\right), \overline{\mathbf{Q}}_t=\mathbf{Q}_1 \mathbf{Q}_2 \cdots \mathbf{Q}_t \tag{25.69}\]同样,我们可以通过以下步骤逆转前向过程:
\[q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)=\frac{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right) q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}=\operatorname{Cat}\left(\boldsymbol{x}_{t-1} \left\lvert\, \frac{\boldsymbol{x}_t \mathbf{Q}_t^{\top} \odot \boldsymbol{x}_0 \overline{\mathbf{Q}}_{t-1}}{\boldsymbol{x}_0 \overline{\mathbf{Q}}_t \boldsymbol{x}_t^{\top}}\right.\right) \tag{25.70}\]我们将在第25.7.3节讨论如何定义生成过程 $p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)$。由于两个分布都可以进行因式分解,我们可以通过对每个维度的KL求和,轻松计算方程(25.67)中的KL分布。
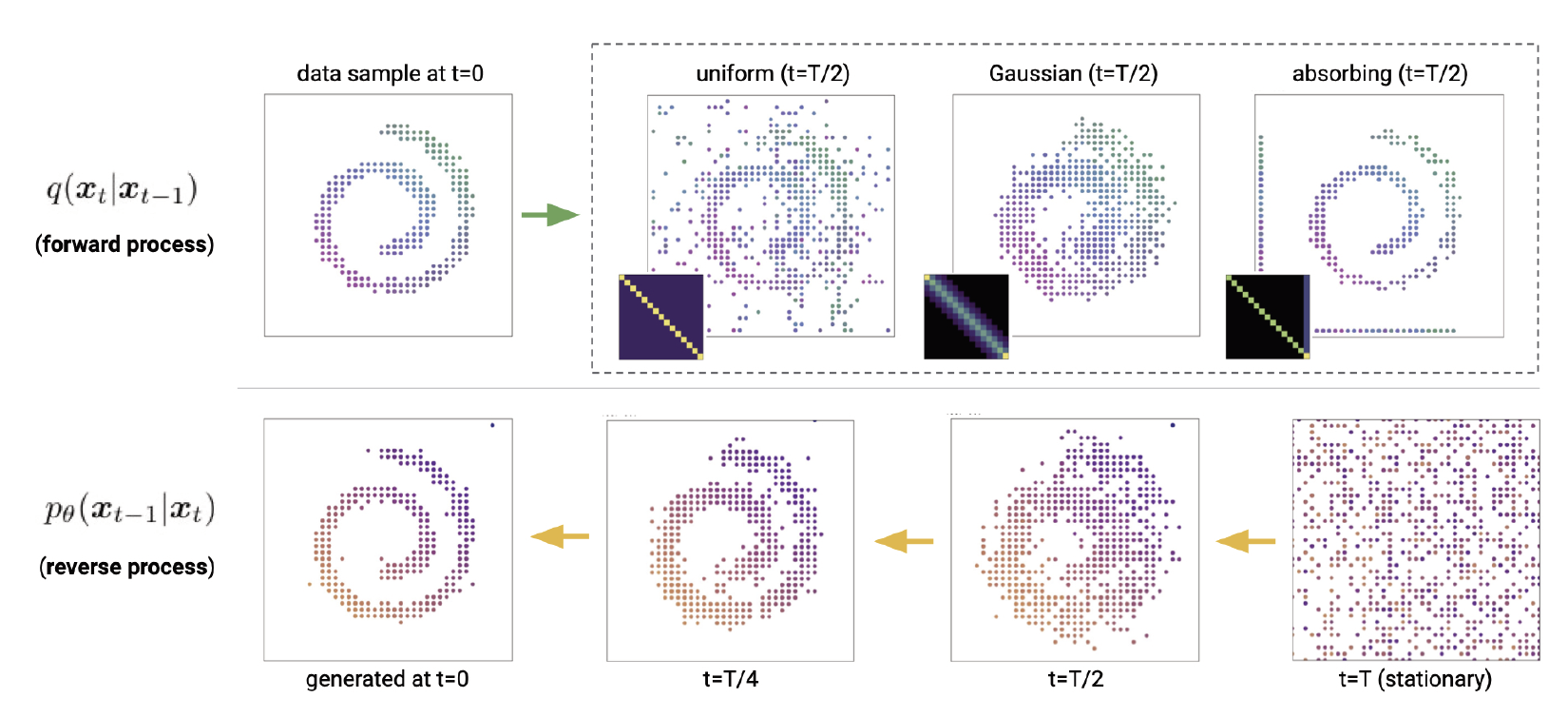
图25.16:。
25.7.2 前向过程中马尔可夫转移矩阵的选择
在这一节中,我们将给出一些转移矩阵 $\mathbf{Q}_t$ 的例子。
一种简单的方法是使用 $\mathbf{Q}_t=\left(1-\beta_t\right) \mathbf{I}+\beta_t / K$,我们可以将其以标量形式写成:
\[\left[\mathbf{Q}_t\right]_{i j}= \begin{cases}1-\frac{K-1}{K} \beta_t & \text { if } i=j \\ \frac{1}{K} \beta_t & \text { if } i \neq j\end{cases} \tag{25.71}\]直观上来说,上述的转移矩阵在 $K$ 个类别上增加了少量的均匀噪声,并且以很大的概率$1-\beta_t$,我们会从 $\boldsymbol{x}_{t-1}$ 中采样。我们称这个为均匀核。由于这是一个具有严格正值的双随机矩阵,所以最终的稳态分布实际上是一个均匀分布。参见图25.16的示意图。
在均匀核的情况下,[Hoo+21][^Hoo21]证明边际分布由下式给出:
\[q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\operatorname{Cat}\left(\boldsymbol{x}_t \mid \bar{\alpha}_t \boldsymbol{x}_0+\left(1-\bar{\alpha}_t\right) / K\right) \tag{25.72}\]其中 $\alpha_t=1-\beta_t$ 且 \(\bar{\alpha}_t=\prod_{\tau=1}^t \alpha_\tau\)。这与第25.2节讨论的高斯情况类似。 此外,我们可以推导出后验分布如下:
\[\begin{align} q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) & =\operatorname{Cat}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{\theta}_{\text {post }}\left(\boldsymbol{x}_t, \boldsymbol{\theta}_0\right)\right), \boldsymbol{\theta}_{\text {post }}\left(\boldsymbol{x}_t, \boldsymbol{\theta}_0\right)=\tilde{\boldsymbol{\theta}} / \sum_{k=1}^K \tilde{\theta}_k \tag{25.73} \\ \tilde{\boldsymbol{\theta}} & =\left[\alpha_t \boldsymbol{x}_t+\left(1-\alpha_t\right) / K\right] \odot\left[\bar{\alpha}_{t-1} \boldsymbol{x}_0+\left(1-\bar{\alpha}_{t-1}\right) / K\right] \tag{25.74} \end{align}\]另一个选择是定义一个特殊的吸收状态(absorbing state) $m$,代表一个掩码令牌,我们以概率 $\beta_t$ 转换为该状态。具体来说,我们有 $\mathbf{Q}_t=\left(1-\beta_t\right) \mathbf{I}+\beta_t \mathbf{1} \boldsymbol{e}_m^{\top}$,或者,用标量形式来表达
\[\left[\mathbf{Q}_t\right]_{i j}= \begin{cases}1 & \text { if } i=j=m \\ 1-\beta_t & \text { if } i=j \neq m \\ \beta_t & \text { if } j=m, i \neq m\end{cases} \tag{25.75}\]这会收敛到状态 $m$ 上的一个点质量分布。参见图 25.16 的示意图。
另一种适合量化序数值的选择是使用离散化的高斯分布,它会转换到其他相近的状态,转换的概率取决于状态在数值上的相似性。如果我们确保转移矩阵是双随机的,那么得到的稳态分布将再次是均匀的。参见图 25.16 的示意图。
25.7.3 逆向过程的参数化
虽然可以使用神经网络 \(f_{\boldsymbol{\theta}}\left(\boldsymbol{x}_t\right)\) 直接预测 \(p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\) 的对数似然,但更可取的做法是直接预测输出的对数似然,使用 \(\tilde{p}_{\boldsymbol{\theta}}\left(\tilde{\boldsymbol{x}}_0 \mid \boldsymbol{x}_t\right)\);然后我们可以将这个与 \(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)\) 的解析表达式结合起来得到
\[p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right) \propto \sum_{\tilde{\boldsymbol{x}}_0} q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \tilde{\boldsymbol{x}}_0\right) \tilde{p}_{\boldsymbol{\theta}}\left(\tilde{\boldsymbol{x}}_0 \mid \boldsymbol{x}_t\right) \tag{25.76}\](如果有$D$个维度,每个维度有$K$个值,那么对 \(\tilde{\boldsymbol{x}}_0\) 的求和需要 \(O(D K)\) 时间。)与直接学习 \(p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\) 相比,这种方法的一个优势是模型将自动满足 \(\mathbf{Q}_t\) 中的任何稀疏性约束。此外,我们可以一次执行 $k$ 步推理,通过预测
\[p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-k} \mid \boldsymbol{x}_t\right) \propto \sum_{\tilde{\boldsymbol{x}}_0} q\left(\boldsymbol{x}_{t-k} \mid \boldsymbol{x}_t, \tilde{\boldsymbol{x}}_0\right) \tilde{p}_{\boldsymbol{\theta}}\left(\tilde{\boldsymbol{x}}_0 \mid \boldsymbol{x}_t\right) \tag{25.77}\]请注意,在多步高斯情况下,我们需要更复杂的模型来处理多模态性(见第25.5.2节)。相比之下,离散分布已经内置了这种灵活性。
25.7.4 噪声计划表
在这一节中,我们讨论如何为 $\beta_t$ 选择噪声进度表。对于离散化高斯扩散,[Aus+21] 建议在离散化步骤之前线性增加高斯噪声的方差。对于均匀扩散,我们可以使用如下形式的余弦进度表 $\alpha_t=\cos \left(\frac{t / T+s}{1+s} \frac{\pi}{2}\right)$,其中 $s=0.08$,正如 [ND21] 所建议的。(回想一下 $\beta_t=1-\alpha_t$,所以随着时间的推移噪声会增加。)对于掩码扩散,我们可以使用如下形式的进度表 $\beta_t=1 /(T-t+1)$,正如 [SD+15b] 所建议的。
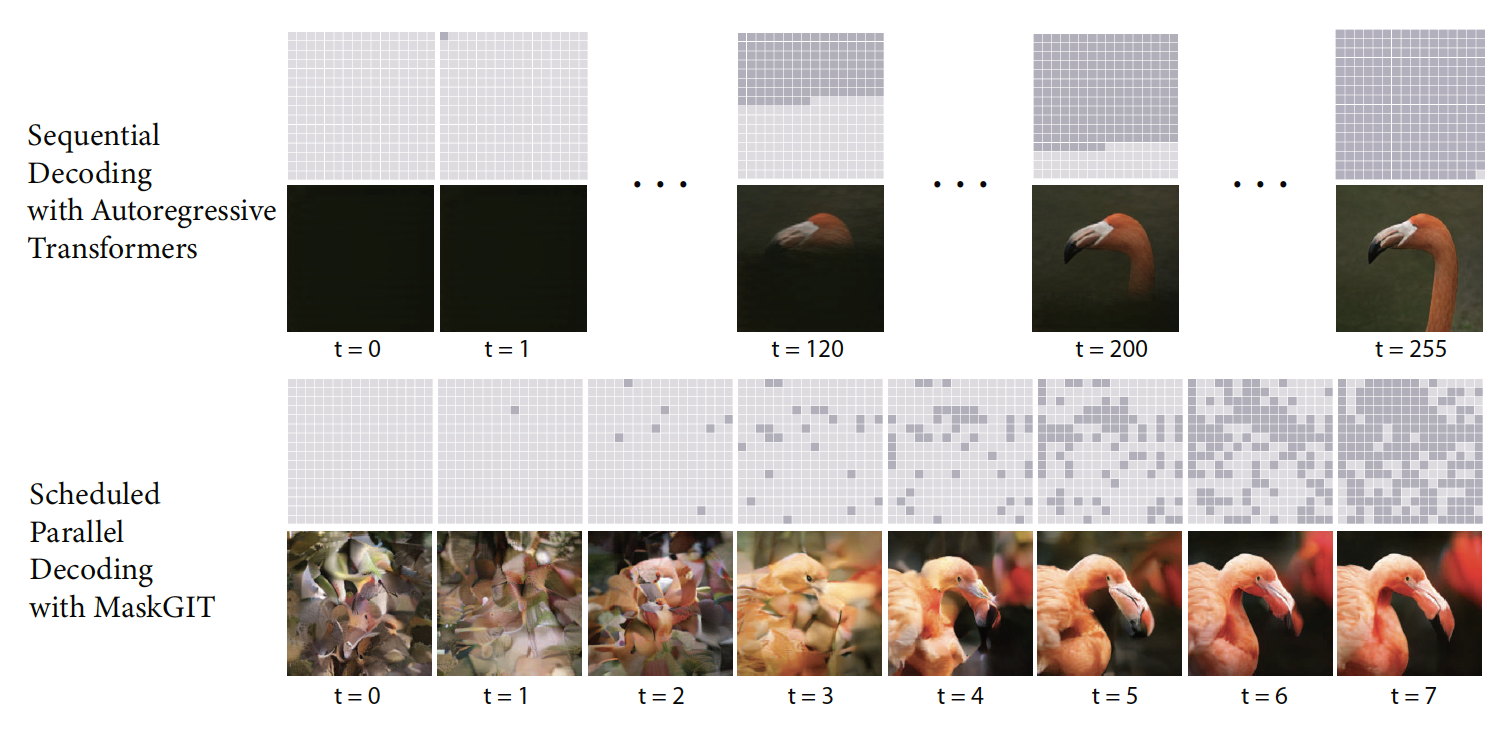
图25.17:。
25.7.5 Connections to other probabilistic models for discrete sequences
D3PM(基于扩散的离散概率模型)与其他概率文本模型之间有着有趣的联系。例如,假设我们将转移矩阵定义为均匀转移矩阵和一个吸收MASK状态的组合,即 $\mathbf{Q}=\alpha \mathbf{1} \boldsymbol{e}_m^{\top}+\beta \mathbf{1} \mathbf{1}^{\top} / K+(1-\alpha-\beta) \mathbf{I}$。对于一个一步扩散过程,其中$q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)$ 用MASK替换了10%的令牌,并且以5%的概率随机替换,我们恢复了用来训练BERT语言模型的相同目标,即
\[L_0\left(\boldsymbol{x}_0\right)=-\mathbb{E}_{q\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_0\right)} \log p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_1\right) \tag{25.78}\](这是因为 $L_T=0$,并且在方程(25.27)中的变分界限中没有使用其他时间步骤。)
现在考虑一个确定性地逐个掩码令牌的扩散过程。对于长度为 $N = T$ 的序列,我们有 \(q\left(\left[\boldsymbol{x}_t\right]_i \mid \boldsymbol{x}_0\right)=\left[\boldsymbol{x}_0\right]_i\) 如果 $i < N - t$(通过),否则 \(\left[\boldsymbol{x}_t\right]_i\) 被设置为 MASK。因为这是一个确定性过程,后验 \(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)\) 是在 $\boldsymbol{x}_t$ 上有一个少的掩码令牌的 delta 函数。然后可以显示 KL 项变成 \(D_{\mathbb{K L}}\left(q\left(\left[\boldsymbol{x}_t\right]_i \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \| p_{\boldsymbol{\theta}}\left(\left[\boldsymbol{x}_{t-1}\right]_i \mid \boldsymbol{x}_t\right)\right)=-\log p_{\boldsymbol{\theta}}\left(\left[\boldsymbol{x}_0\right]_i \mid \boldsymbol{x}_t\right)\),这是自回归模型的标准交叉熵损失。
最后,可以证明生成掩码的语言模型,如 [WC19; Gha+19],也对应于离散扩散过程:序列以所有位置都被掩码的方式开始,每一步,一组令牌在给定前一个序列的情况下被生成。[Cha+22] 的 MaskGIT 方法在图像领域中使用了类似的过程,这是在对图像块应用矢量量化之后。这些并行的、迭代的解码器要比顺序的自回归解码器快得多。参见图 25.17 的示意图。
【McA23】 ↩
【Kin21】 D. P. Kingma, T. Salimans, B. Poole, and J. Ho. “Variational Diffusion Models”. In: NIPS. July 2021. ↩ ↩2 ↩3
稍后我们将讨论一些扩展内容,其中包括编码器的噪音水平也可以学习。尽管如此,编码器的设计仍然很简单。 ↩
我们只需要使用高斯分布的贝叶斯规则。例如,可以参考 https://lilianweng.github.io/posts/2021-07-11-diffusion-models/ 来查看详细的推导过程。 ↩
【Cho22】 J. Choi, J. Lee, C. Shin, S. Kim, H. Kim, and S. Yoon. “Perception Prioritized Training of Diffusion Models”. In: CVPR. Apr. 2022. ↩
此处的loss采用了简化的形式,即连续时间极限情况下的结果。极限情况下的loss形式我们将在25.4节讨论。 ↩
【Gao+21】 ↩
【XKV22】 ↩
【SH22】 ↩