2 概率

本章，我们介绍概率论。

2.1 简介
2.2 一些常用的概率分布
2.3 高斯联合分布
2.4 指数族分布
2.5 Transformations of random variables
2.6 马尔可夫链
2.7 概率分布之间的距离测度

2.1 简介

在本节中，我们将正式定义概率，参考 [Cha21]¹ 第2章的内容。其他关于该主题的优秀介绍可以参考 [GS97]²; [BT08]³; [Bet18]⁴; [DFO20]⁵ 。

2.1.1 概率空间

概率空间（probability space）定义为一个三元组 $(\Omega, \mathcal{F}, P)$，其中 $ \Omega $ 表示样本空间（sample space），是某个实验所有可能结果的集合；$ \mathcal{F} $ 表示事件空间（event space），是 $ \Omega $ 集合的所有可能子集的集合；而 $ P $ 表示概率测度（probability measure），是从事件 $ E \in \mathcal{F} $ 到区间 $ [0, 1] $ 中某个数的映射（即 $ P: \mathcal{F} \to [0, 1] $），它满足某些约束，这些约束将在第 2.1.4 节中讨论。

2.1.2 离散随机变量

最简单的设定是实验结果构成的是一个可数集合。例如，考虑投掷一个包含 $3$ 个面的骰子，每个面分别标记为“A”、“B”和“C”。（选择3面而不是6面是为了方便分析。）此时的样本空间 $\Omega = \{A, B, C\}$ 表示“实验”的所有可能结果。事件空间是样本空间的所有可能子集的集合，因此 $\mathcal{F} = \left\{ \emptyset, \{A\}, \{B\}, \{C\}, \{A, B\}, \{A, C\}, \{B, C\}, \{A, B, C\} \right\}$。单个事件实际上就是事件空间的某个元素。例如，事件 $E_1 = \{A, B\}$ 表示骰子显示面为A或B的结果，而事件 $E_2 = \{C\}$ 表示骰子显示面C的结果。

一旦我们定义了事件空间，我们需要指定概率测度，它提供了一种计算事件空间中每个集合的“大小”或“权重”的方法。在3面的骰子示例中，假设我们定义每个实验结果（原子事件）的概率为 $P[\{ A \}] = \frac{2}{6}$，$P[\{B\}] = \frac{1}{6}$，和 $P[\{C\}] = \frac{3}{6}$。接下来，我们可以通过将每个结果的概率测度相加来推导出其他事件的概率，例如 $P[\{A, B\}] = \frac{2}{6} + \frac{1}{6} = \frac{1}{2}$。我们将在第2.1.4节中给出正式的定义。

为了简化符号，我们将为事件空间中的每个可能结果分配一个数字。这可以通过定义随机变量（random variable, rv）来完成，随机变量是一个函数 $ X : \Omega \to \mathbb{R} $，它将某个实验结果 $ \omega \in \Omega $ 映射到实数域上的某个数字 $ X(\omega) $。例如，我们可以为3面骰子定义随机变量 $ X $，使得 $ X(A) = 1 $，$ X(B) = 2 $，$ X(C) = 3 $。作为另一个例子，考虑一个实验——公平地掷两次硬币。样本空间为 $ \Omega = { \omega_1 = (H, H), \omega_2 = (H, T), \omega_3 = (T, H), \omega_4 = (T, T) } $，其中 $ H $ 代表正面，$ T $ 代表反面。设 $ X $ 为表示正面数量的随机变量。则我们有 $ X(\omega_1) = 2 $，$ X(\omega_2) = 1 $，$ X(\omega_3) = 1 $，$ X(\omega_4) = 0 $。

我们将随机变量可能取值的集合定义为状态空间（state space），记作 $ X(\Omega) = X $。我们使用以下方式定义任意给定状态的概率：

\[p_X(a)=\mathbb{P}[X=a]=\mathbb{P}\left[X^{-1}(a)\right] \tag{2.1}\]

其中 $X^{-1}(a) = \{ \omega \in \Omega \mid X(\omega) = a \}$ 是 $ a $ 的逆变换。这里 $ p_X $ 被称为随机变量 $ X $ 的概率质量函数（probability mass function, pmf）。在抛两次公平硬币的示例中，pmf 为 $p_X(0) = P[\{(T, T)\}] = \frac{1}{4}$，$p_X(1) = P[\{(T, H), (H, T)\}] = \frac{2}{4}$，和 $p_X(2) = P[\{(H, H)\}] = \frac{1}{4}$。pmf 可以通过直方图或某些参数化函数表示（见第2.2.1节）。我们称 $ p_X $ 为随机变量 $ X $ 的概率分布（probability distribution）。通常在上下文明确时，我们会省略 $ p_X $ 中的 $ X $ 下标。

2.1.3 连续随机变量

接下来考虑具有连续结果的实验。在这种情况下，我们假设样本空间是实数域的某个子集 $ \Omega \subseteq \mathbb{R} $，并将每个连续随机变量定义为恒等函数 $ X(\omega) = \omega $。

例如，考虑某个事件的持续时间（以秒为单位）。我们定义样本空间为 $\Omega = \{ t : 0 \leq t \leq T_{\text{max}} \}$。由于这是一个不可数集合，我们不能像离散情况那样通过枚举定义所有可能的子集。相反，我们需要根据Borel sigma-field定义事件空间，也称为Borel sigma-algebra。我们说 $ \mathcal{F} $ 是一个 $\sigma$-域，如果满足以下条件：(1) $ \emptyset \in \mathcal{F} $ 且 $ \Omega \in \mathcal{F} $；(2) $ \mathcal{F} $ 对补集是封闭的，即如果 $ E \in \mathcal{F} $，则 $ E^c \in \mathcal{F} $；(3) $ \mathcal{F} $ 对可数集合的并集与交集也是封闭的，这意味着如果 $ E_1, E_2, \ldots \in \mathcal{F} $，则 $ \bigcup_{i=1}^{\infty} E_i \in \mathcal{F} $ 和 $ \bigcap_{i=1}^{\infty} E_i \in \mathcal{F} $。最后，我们说 $ \mathcal{B} $ 是一个Borel sigma-field，如果它是由形式为 $(-\infty, b] = \{ x : -\infty < x \leq b \}$ 的半闭区间生成的 $\sigma$-域。通过取这些区间的并、交和补集，我们可以看到 $ \mathcal{B} $ 包含以下集合：

\[(a, b),\left[a, b\right],(a, b],[a, b),\{b\},-\infty \leq a \leq b \leq \infty \tag{2.2}\]

在我们的连续时间示例中，我们可以进一步限制事件空间，使其只包含下限为$0$且上限为 $T_{\text{max}}$ 的区间。

为了定义概率测度，我们为每个 $x \in \Omega$ 分配一个权重函数 $p_X(x) \geq 0$，称为概率密度函数（probability density function, pdf）。有关常见概率密度函数，请参见第2.2.2节。然后，我们可以使用以下公式推导事件 $E = [a, b]$ 发生的概率：

\[\mathbb{P}([a, b])=\int_E d \mathbb{P}=\int_a^b p(x) d x \tag{2.3}\]

我们还可以为随机变量 $X$ 定义累积分布函数（cumulative distribution function, cdf）：

\[P_X(x) \triangleq \mathbb{P}[X \leq x]=\int_{-\infty}^x p_X\left(x^{\prime}\right) d x^{\prime} \tag{2.4}\]

由此，我们可以通过以下公式计算区间的概率：

\[\mathbb{P}([a, b])=p(a \leq X \leq b)=P_X(b)-P_X(a) \tag{2.5}\]

术语“概率分布”可以指代概率密度函数 $p_X$、累积分布函数 $P_X$ 或者概率测度 $\mathbb{P}$。

我们可以将上述定义推广到多维空间 $\mathbb{R}^n$，以及更复杂的样本空间，例如函数。

2.1.4 概率公理

与事件空间相关的概率法则必须遵循概率公理（axioms of probability），也称为科尔莫哥洛夫公理（Kolmogorov axioms），其内容如下：

非负性：对于任何事件$E \subseteq \Omega$，有 $ P[E] \geq 0 $。
规范化：整个样本空间的概率为1，即 $ P[\Omega] = 1 $。
可加性：对于任意可数序列的两两不相交集合 $\left\{E_1, E_2, \ldots,\right\}$，我们有：
\[\mathbb{P}\left[\cup_{i=1}^{\infty} E_i\right]=\sum_{i=1}^{\infty} \mathbb{P}\left[E_i\right] \tag{2.6}\]
在有限情况下，当我们只有两个不相交的集合 $E_1$ 和 $E_2$ 时，上式可写成：
\[\mathbb{P}\left[E_1 \cup E_2\right]=\mathbb{P}\left[E_1\right]+\mathbb{P}\left[E_2\right] \tag{2.7}\]
这对应于事件 $E_1$ 或 $E_2$ 的概率，此时的事件是互斥的（不相交的集合）。
从这些公理，我们可以推导出补充规则（complement rule）：
\[\mathbb{P}\left[E^c\right]=1-\mathbb{P}[E] \tag{2.8}\]

其中 $E^c = \bar{E}$ 是事件 $E$ 的补集。（这是因为 $P[\Omega] = 1 = P[E \cup E^c] = P[E] + P[E^c]$）。我们还可以证明 $P[E] \leq 1$（通过反证法），以及 $P[\emptyset] = 0$（这从第一个推论中得出，当 $E = \emptyset$ 时）。

我们还可以证明以下结果，称为加法规则：

\[\mathbb{P}\left[E_1 \cup E_2\right]=\mathbb{P}\left[E_1\right]+\mathbb{P}\left[E_2\right]-\mathbb{P}\left[E_1 \cap E_2\right] \tag{2.9}\]

这适用于任何一对事件，即使它们不是互斥的。

2.1.5 条件概率

考虑两个事件$E_1$ 和 $E_2$。如果 $ P[E_2] \neq 0 $，我们定义事件 $ E_1 $ 在给定 $ E_2 $ 下的条件概率（conditional probability）为：

\[\mathbb{P}\left[E_1 \mid E_2\right] \triangleq \frac{\mathbb{P}\left[E_1 \cap E_2\right]}{\mathbb{P}\left[E_2\right]} \tag{2.10}\]

由此，我们可以得到乘法规则（multiplication rule）：

\[\mathbb{P}\left[E_1 \cap E_2\right]=\mathbb{P}\left[E_1 \mid E_2\right] \mathbb{P}\left[E_2\right]=\mathbb{P}\left[E_2 \mid E_1\right] \mathbb{P}\left[E_1\right] \tag{2.11}\]

条件概率衡量了事件 $E_1$ 在事件 $E_2$ 已发生的情况下发生的可能性。然而，如果这两个事件无关，概率将不会改变。正式地，我们说事件 $E_1$ 和 $E_2$ 是独立事件（independent events），如果：

\[\mathbb{P}\left[E_1 \cap E_2\right]=\mathbb{P}\left[E_1\right] \mathbb{P}\left[E_2\right] \tag{2.12}\]

如果 $\mathbb{P}\left[E_1\right]>0$ 且 $\mathbb{P}\left[E_2\right]>0$，这等价于要求 $P[E_1 \mid E_2] = P[E_1]$，或者等价地，$P[E_2 \mid E_1] = P[E_2]$。类似地，我们说事件 $E_1$ 和 $E_2$ 在给定 $E_3$ 的情况下是条件独立的，如果

\[\mathbb{P}\left[E_1 \cap E_2 \mid E_3\right]=\mathbb{P}\left[E_1 \mid E_3\right] \mathbb{P}\left[E_2 \mid E_3\right] \tag{2.13}\]

根据条件概率的定义，我们可以推导出全概率法则（law of total probability），它表明：如果$\left\{A_1, \ldots, A_n\right\}$ 是样本空间 $\Omega$ 的一个划分，那么对于任何事件 $B \subseteq \Omega$，我们有：

\[\mathbb{P}[B]=\sum_{i=1}^n \mathbb{P}\left[B \mid A_i\right] \mathbb{P}\left[A_i\right] \tag{2.14}\]

2.1.6 贝叶斯定理

从条件概率的定义出发，我们可以推导出贝叶斯定理（Bayes’ rule），也称为贝叶斯法则（Bayes’theorem），它指出，对于任意两个事件 $ E_1 $ 和 $ E_2 $，只要 $ P[E_1] > 0 $ 且 $ P[E_2] > 0 $，我们有：

\[\mathbb{P}\left[E_1 \mid E_2\right]=\frac{\mathbb{P}\left[E_2 \mid E_1\right] \mathbb{P}\left[E_1\right]}{\mathbb{P}\left[E_2\right]} \tag{2.15}\]

对于一个具有 $ K $ 种可能状态的离散随机变量 $ X $，我们可以使用全概率法则将贝叶斯定理写为：

\[p(X=k \mid E)=\frac{p(E \mid X=k) p(X=k)}{p(E)}=\frac{p(E \mid X=k) p(X=k)}{\sum_{k^{\prime}=1}^K p\left(E \mid X=k^{\prime}\right) p\left(X=k^{\prime}\right)} \tag{2.16}\]

此处 $ P(X = k) $ 表示先验概率（prior probability），$P(E \mid X = k)$ 表示似然（likelihood），$P(X = k \mid E)$ 是后验概率（posterior probability），而 $ P(E) $ 是归一化常数，称为边际似然（marginal likelihood）。

类似地，对于一个连续随机变量 $ X $，我们可以将贝叶斯定理写为：

\[p(X=x \mid E)=\frac{p(E \mid X=x) p(X=x)}{p(E)}=\frac{p(E \mid X=x) p(X=x)}{\int p\left(E \mid X=x^{\prime}\right) p\left(X=x^{\prime}\right) d x^{\prime}} \tag{2.17}\]

2.2 一些常用的概率分布

在下面的章节中，我们总结了一些常用的概率分布。有关更多信息，请参见补充章节 2，以及此处了解一些交互式可视化的结果。

2.2.1 离散分布

在本节中，我们讨论一些定义在（非负）整数子集上的离散分布。

2.2.1.1 伯努利分布和二项分布

令 $ x \in {0, 1, \ldots, N} $。二项分布（binomial distribution）由以下公式定义：

\[\operatorname{Bin}(x \mid N, \mu) \triangleq\binom{N}{x} \mu^x(1-\mu)^{N-x} \tag{2.18}\]

其中 $\binom{N}{k} \triangleq \frac{N!}{(N-k)!k!}$ 是从 $ N $ 个项目中选择 $ k $ 个元素的方式（这被称为二项系数，读作“从 $ N $ 中选择 $ k $”）。

如果 $ N = 1 $，此时 $ x \in {0, 1} $，则二项分布简化为伯努利分布（Bernoulli distribution）：

\[\operatorname{Ber}(x \mid \mu)= \begin{cases}1-\mu & \text { if } x=0 \\ \mu & \text { if } x=1\end{cases} \tag{2.19}\]

其中 $ \mu = E[X] = P(X = 1) = p $ 是均值。

2.2.1.2 分类分布和多项分布

如果变量的取值范围为 $x \in{1, \ldots, K}$，我们可以使用分类（categorical）分布：

\[\operatorname{Cat}(x \mid \boldsymbol{\theta}) \triangleq \prod_{k=1}^K \theta_k^{\mathrm{I}(x=k)} \tag{2.20}\]

另外，我们可以用一维one-hot编码向量 $ \boldsymbol{x} $ 来表示这个 $ K $-value 变量 $ x $，此时式（2.20）可以写成：

\[\operatorname{Cat}(\boldsymbol{x} \mid \boldsymbol{\theta}) \triangleq \prod_{k=1}^K \theta_k^{x_k} \tag{2.21}\]

如果 $ \boldsymbol{x} $ 的第 $ k $ 个元素表示值 $ k $ 在 $ N = \sum_{k=1}^{K} x_k $ 次试验中出现的次数，那么我们得到多项分布（multinomial distribution）：

\[\mathcal{M}(\boldsymbol{x} \mid N, \boldsymbol{\theta}) \triangleq\binom{N}{x_1 \ldots x_K} \prod_{k=1}^K \theta_k^{x_k} \tag{2.22}\]

其中多项式系数（multinomial coefficient）定义为：

\[\binom{N}{k_1 \ldots k_m} \triangleq \frac{N!}{k_{1}!\ldots k_{m}!} \tag{2.23}\]

2.2.1.3 泊松分布

假设 $ X \in {0, 1, 2, \ldots} $。我们称随机变量 $ X $ 服从参数 $ \lambda > 0 $ 的泊松分布（Poisson distribution），记作 $ X \sim \text{Poi}(\lambda) $，如果它的概率质量函数（PMF）为：

\[\operatorname{Poi}(x \mid \lambda)=e^{-\lambda} \frac{\lambda^x}{x!} \tag{2.24}\]

其中 $ \lambda $ 表示 $ X $ 的均值（和方差）。泊松分布描述了单位时间内随机事件发生的次数，适用于事件发生率稳定且独立的情况。

2.2.1.4 负二项分布

假设我们有一个“urn”（罐子），装有 $ N $ 个球，其中$ R $ 个是红色，$ B $ 个是蓝色。假设我们进行可放回的抽样（sampling with replacement），直到我们得到 $ n \geq 1 $ 个球。令 $ X $ 为其中蓝色球的数量。可以证明 $ X \sim \text{Bin}(n, p) $，其中 $ p = \frac{B}{N} $ 是蓝色球的比例；因此 $ X $ 服从我们在 2.2.1.1 节讨论的二项分布。

现在假设将抽到红球视为“失败”，将抽到蓝球视为“成功”。我们持续抽样，直到观察到 $ r $ 次失败。令 $ X $ 表示成功（蓝球）的数量，可以证明 $ X \sim \text{NegBinom}(r, p) $，负二项分布（negative binomial distribution）定义为：

\[\operatorname{NegBinom}(x \mid r, p) \triangleq\binom{x+r-1}{x}(1-p)^r p^x \tag{2.25}\]

其中 $ x \in {0, 1, 2, \ldots} $。（如果 $ r $ 是实数，我们用 $\frac{\Gamma(x+r)}{x!\Gamma(r)}$ 替换 $\binom{x+r-1}{x}$ ，其中我们利用 $ (x - 1)! = \Gamma(x) $ 的事实。）

该分布具有以下矩（moments）：

\[\mathbb{E}[x]=\frac{p r}{1-p}, \mathbb{V}[x]=\frac{p r}{(1-p)^2} \tag{2.26}\]

这个双参数分布比泊松分布具有更大的建模灵活性，因为它可以分别表示均值和方差。这在建模“传染性”事件时特别有用，这些事件的发生是正相关的，导致方差比独立事件的情况更大。实际上，泊松分布是负二项分布的特例，因为可以证明：$\operatorname{Poi}(\lambda)=\lim _{r \rightarrow \infty} \operatorname{NegBinom}\left(r, \frac{\lambda}{1+\lambda}\right)$ 。另一个特例是当 $ r = 1 $ 时，这被称为几何分布（geometric distribution）。

2.2.2 实数域上的连续分布

在本节中，我们讨论一些定义在实数域的单变量概率分布 $ p(x) $，其中 $ x \in \mathbb{R} $。

2.2.2.1 高斯分布（正态分布）

最广泛使用的单变量分布是高斯分布（Gaussian distribution），也称为正态分布（normal distribution）。（关于这些名称的讨论，请参阅[Mur22][^Mur22]第2.6.4节。）高斯分布的概率密度函数（pdf）由下式给出：

\[\mathcal{N}\left(x \mid \mu, \sigma^2\right) \triangleq \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{1}{2 \sigma^2}(x-\mu)^2} \tag{2.27}\]

其中 $ \frac{1}{\sqrt{2\pi\sigma^2}} $ 是归一化常数，确保密度的积分为1。参数 $ \mu $ 表示分布的均值，也称为众数。参数 $ \sigma^2 $ 表示分布的方差。有时我们讨论高斯分布的精度（precision），指的是方差的倒数：$ \tau = \frac{1}{\sigma^2} $。高精度意味着以 $ \mu $ 为中心的分布更窄（方差低）。

高斯分布的累积分布函数（CDF）定义为：

\[\Phi\left(x ; \mu, \sigma^2\right) \triangleq \int_{-\infty}^x \mathcal{N}\left(z \mid \mu, \sigma^2\right) d z \tag{2.28}\]

如果 $ \mu = 0 $ 且 $ \sigma = 1 $（被称为标准正态分布），我们简单地写作 $ \Phi(x) $。

2.2.2.2 半正态分布

对于某些场景，我们希望在非负实数上定义一个分布。构建这样一个分布的一种方法是定义 $Y = \lvert X \rvert$，其中 $X \sim N(0, \sigma^2)$。由此产生的关于 $ Y $ 的分布被称为半正态分布（half-normal distribution），其概率密度函数（pdf）定义为：

\[\mathcal{N}_{+}(y \mid \sigma) \triangleq 2 \mathcal{N}\left(y \mid 0, \sigma^2\right)=\frac{\sqrt{2}}{\sigma \sqrt{\pi}} \exp \left(-\frac{y^2}{2 \sigma^2}\right) \quad y \geq 0 \tag{2.29}\]

这可以被看作是将 $ N(0, \sigma^2) $ 分布“折叠”到自身上。

2.2.2.3 学生t分布

高斯分布的一个问题是它对异常值很敏感，因为概率随着与中心的（平方）距离呈指数级快速衰减。一个更稳健的分布是学生t分布（Student t-distribution），简称为学生分布（Student distribution）。其概率密度函数（pdf）定义如下：

\[\begin{align} \mathcal{T}_\nu\left(x \mid \mu, \sigma^2\right) & =\frac{1}{Z}\left[1+\frac{1}{\nu}\left(\frac{x-\mu}{\sigma}\right)^2\right]^{-\left(\frac{\nu+1}{2}\right)} \tag{2.30}\\ Z & =\frac{\sqrt{\nu \pi \sigma^2} \Gamma\left(\frac{\nu}{2}\right)}{\Gamma\left(\frac{\nu+1}{2}\right)}=\sqrt{\nu} \sigma B\left(\frac{1}{2}, \frac{\nu}{2}\right) \tag{2.31} \end{align}\]

其中 $ \mu $ 表示均值，$ \sigma > 0 $ 是尺度参数（不是标准差），$ \nu > 0 $ 被称为自由度（尽管一个更好的术语可能是“正态度”[Kru13]⁶，因为 $ \nu $ 值越大，分布表现得越像高斯分布）。这里的 $ \Gamma(a) $ 是伽玛函数（gamma function），定义为：

\[\Gamma(a) \triangleq \int_0^{\infty} x^{a-1} e^{-x} d x \tag{2.32}\]

并且 $ B(a; b) $ 是贝塔函数（beta function），定义为：

\[B(a, b) \triangleq \frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)} \tag{2.33}\]

2.2.2.4 柯西分布（Cauchy distribution）

如果 $ \nu = 1 $，学生分布被称为柯西（Cauchy）分布或洛伦兹（Lorentz）分布。其概率密度函数（pdf）定义为：

\[\mathcal{C}(x \mid \mu, \gamma)=\frac{1}{Z}\left[1+\left(\frac{x-\mu}{\gamma}\right)^2\right]^{-1} \tag{2.34}\]

其中 $ Z = \frac{1}{\sqrt{2}} $。这种分布以其尾部过重而著称，以至于定义均值的积分无法收敛。 半柯西（half Cauchy）分布是柯西分布（均值为0）的一个变种，它被“折叠”在自身上，因此其所有的概率密度都在正实数上。因此，它具有以下形式：

\[\mathcal{C}_{+}(x \mid \gamma) \triangleq \frac{2}{\pi \gamma}\left[1+\left(\frac{x}{\gamma}\right)^2\right]^{-1} \tag{2.35}\]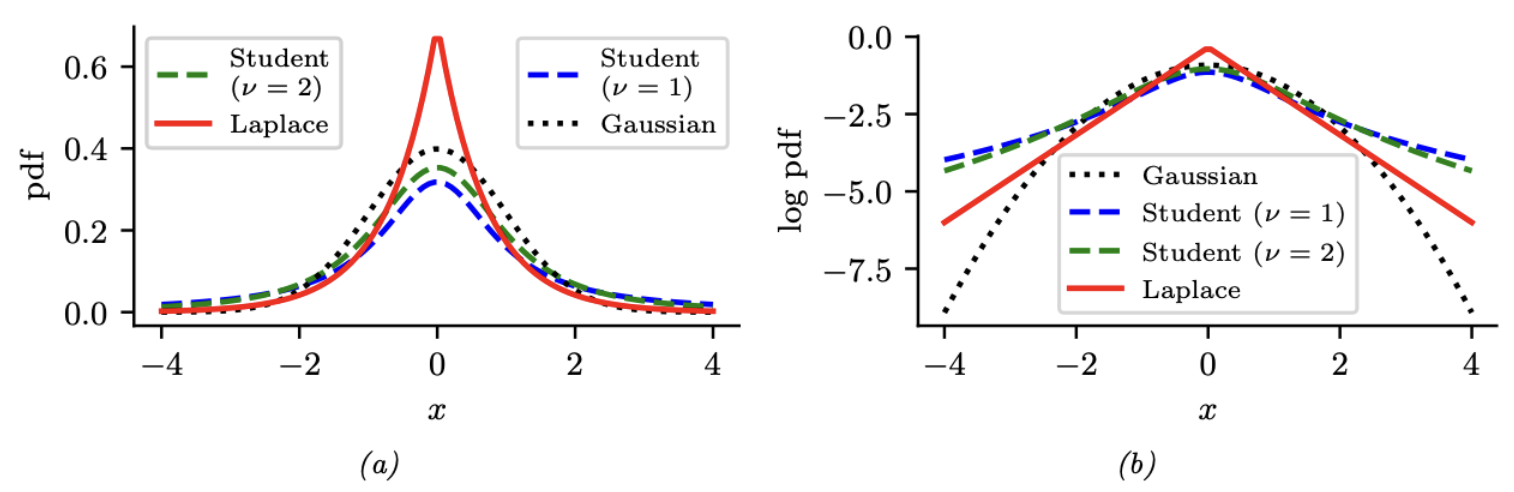

图 $2.1$：(a) $\mathcal{N}(0,1)$，$\mathcal{T}_1(0,1)$以及 $\mathrm{Laplace}(0,1/\sqrt{2})$ 的pdf。高斯分布和拉普拉斯分布的期望和方差分别为 $0$ 和 $1$。学生分布的期望在 $\nu=1$ 时无法定义。(b) pdf 的对数。请注意，与拉普拉斯分布不同，Student分布对于任何参数值都不是对数凹形分布。然而，两者都是单峰的。

2.2.2.5 拉普拉斯分布

另一种具有重尾的分布是拉普拉斯分布（Laplace distribution），也被称为双指数分布（double sided exponential）。其概率密度函数（pdf）如下所示：

\[\operatorname{Laplace}(x \mid \mu, b) \triangleq \frac{1}{2 b} \exp \left(-\frac{|x-\mu|}{b}\right) \tag{2.36}\]

这里的 $\mu$ 是一个位置参数，$b > 0$ 是一个尺度参数。请参考图2.1查看图形。

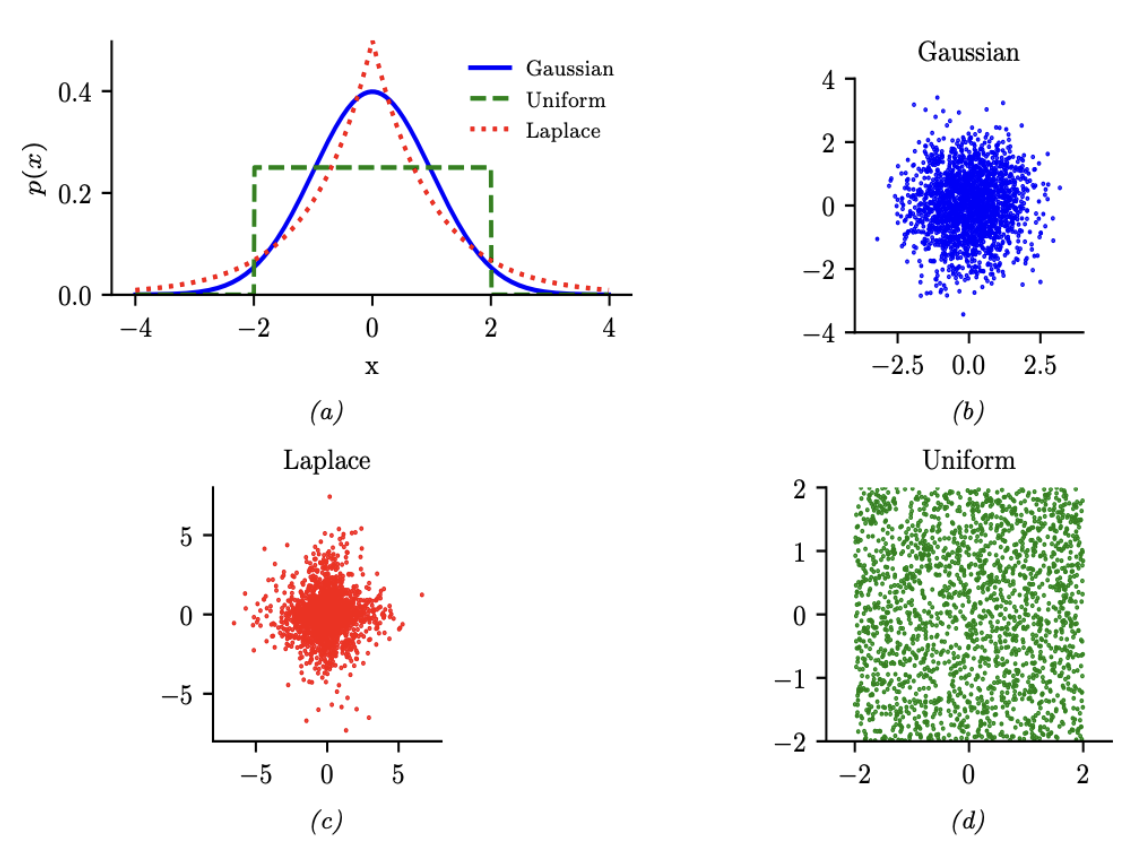
图 $2.2$：1d和2d中高斯（蓝色）、亚高斯（均匀，绿色）和超高斯（拉普拉斯，红色）分布的图示。

2.2.2.6 亚高斯分布（ Sub-Gaussian Distributions ）和超高斯分布（ Super-Gaussian Distributions ）

有两种主要的高斯分布变体，被称为超高斯（super-Gaussian）或尖峰态（leptokurtic）（“Lepto”是希腊语，意为“窄”）和亚高斯（sub-Gaussian）或扁峰态（platykurtic）（“Platy”是希腊语，意为“宽”）。这些分布在它们的峰度（kurtosis）方面有所不同，峰度是衡量它们尾部轻重的一个指标（即，密度远离均值时衰减到零的速度有多快）。更精确地说，峰度定义为：

\[\operatorname{kurt}(z) \triangleq \frac{\mu_4}{\sigma^4}=\frac{\mathbb{E}\left[(Z-\mu)^4\right]}{\left(\mathbb{E}\left[(Z-\mu)^2\right]\right)^2} \tag{2.37}\]

其中 $ \sigma $ 是标准差，$ \mu_4 $ 是第四中心矩（central moment）。（因此 $ \mu_1 = \mu $ 是均值，$ \mu_2 = \sigma^2 $ 是方差。）对于标准高斯分布，峰度是3，所以一些作者将超额峰度（excess kurtosis）定义为自身峰度减去3。一个超高斯分布（例如，拉普拉斯分布）具有正的超额峰度，因此尾部比高斯分布更重。一个亚高斯分布，如均匀分布，具有负的超额峰度，因此尾部比高斯分布更轻。请参考图2.2。

2.2.3 在实数正半轴上的连续分布

在这一部分，我们讨论一些定义在正实数上的单变量分布，即 $x \in \mathbb{R}^+$ 的 $p(x)$。

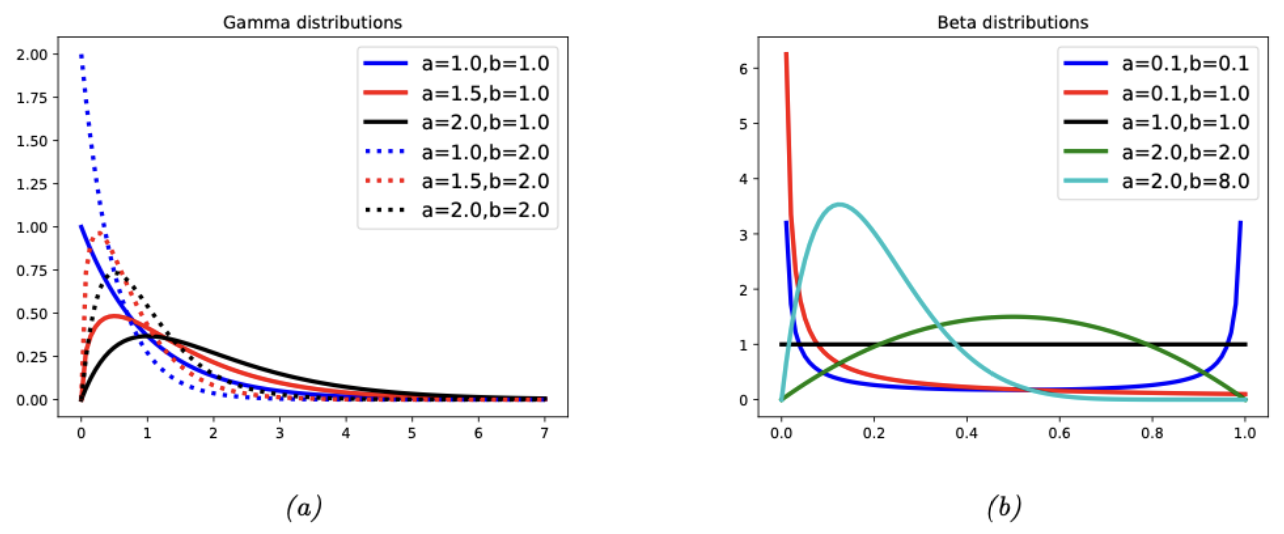
图 $2.3$：（a）伽马分布。如果$a≤1$，则峰值为0；否则峰值远离0。当我们增加速率$b$时，我们减小了水平尺度，从而向左和向上挤压所有概率。（b） beta分布。如果$a<1$，我们在左边得到一个“尖峰”，如果$b<1$，在右边得到一个”尖峰“。如果$a=b=1$，则分布是均匀的。如果$a>1$且$b>1$，则分布为单峰分布。

2.2.3.1 Gamma 分布

伽马分布（gamma distribution）是一种适用于正值实数随机变量 $x > 0$ 的灵活分布。它由两个参数定义，称为形状参数 $a > 0$ 和速率参数 $b > 0$：

\[\mathrm{Ga}(x \mid \text { shape }=a, \text { rate }=b) \triangleq \frac{b^a}{\Gamma(a)} x^{a-1} e^{-x b} \tag{2.38}\]

有时，该分布以速率参数 $a$ 和尺度参数 $s = \frac{1}{b}$ 来参数化：

\[\mathrm{Ga}(x \mid \text { shape }=a, \text { scale }=s) \triangleq \frac{1}{s^a \Gamma(a)} x^{a-1} e^{-x / s} \tag{2.39}\]

请参考图2.3a以获得说明。

2.2.3.2 指数分布

指数分布（exponential distribution）是伽马分布的一个特例，定义为：

\[\operatorname{Expon}(x \mid \lambda) \triangleq \mathrm{Ga}(x \mid \text { shape }=1, \text { rate }=\lambda) \tag{2.40}\]

这个分布描述了泊松过程中事件发生之间的时间，在柏松过程中，事件以恒定的平均速率 $ \lambda $ 连续且独立地发生。

2.2.3.3 卡方分布（Chi-squared distribution）

卡方分布（chi-squared distribution）是伽马分布的一个特例，定义为：

\[\chi_\nu^2(x) \triangleq \mathrm{Ga}\left(x \mid \text { shape }=\frac{\nu}{2}, \text { rate }=\frac{1}{2}\right) \tag{2.41}\]

其中 $\nu$ 被称为自由度。这是高斯随机变量平方和的分布。更精确地说，如果 $Z_i \sim N(0, 1)$，并且 $S = \sum_{i=1}^{\nu} Z_i^2$，那么 $S \sim \chi^2_{\nu}$。因此，如果 $X \sim N(0, \sigma^2)$ 那么 $X^2 \sim \sigma^2 \chi^2_{1}$。由于 $E\left[\chi^2_{1}\right] = 1$ 且 $V\left[\chi^2_{1}\right] = 2$，我们有：

\[\mathbb{E}\left[X^2\right]=\sigma^2, \mathbb{V}\left[X^2\right]=2 \sigma^4 \tag{2.42}\]

2.2.3.4 逆Gamma分布

逆伽马分布（inverse gamma distribution），记作 $Y \sim \text{IG}(a; b)$，是 $Y = \frac{1}{X}$ 的分布，假设 $X \sim \text{Ga}(a; b)$。这个概率密度函数（pdf）定义为：

\[\text { IG }(x \mid \text { shape }=a, \text { scale }=b) \triangleq \frac{b^a}{\Gamma(a)} x^{-(a+1)} e^{-b / x} \tag{2.43}\]

均值仅在 $a > 1$ 时存在。方差仅在 $a > 2$ 时存在。

缩放逆卡方分布（scaled inverse chi-squared）是逆伽马分布的一种重参数化版本：

\[\begin{align} \chi^{-2}\left(x \mid \nu, \sigma^2\right) & =\mathrm{IG}\left(x \mid \text { shape }=\frac{\nu}{2}, \text { scale }=\frac{\nu \sigma^2}{2}\right) \tag{2.44}\\ & =\frac{1}{\Gamma(\nu / 2)}\left(\frac{\nu \sigma^2}{2}\right)^{\nu / 2} x^{-\frac{\nu}{2}-1} \exp \left(-\frac{\nu \sigma^2}{2 x}\right) \tag{2.45} \end{align}\]

特别地，当 $\nu \sigma^2 = 1$（即 $\sigma^2 = \frac{1}{\nu}$）时，对应于 $\text{IG}(\frac{\nu}{2}; \frac{1}{2})$，这种分布也被称为逆卡方分布 $\chi_\nu^{-2}(x)$。

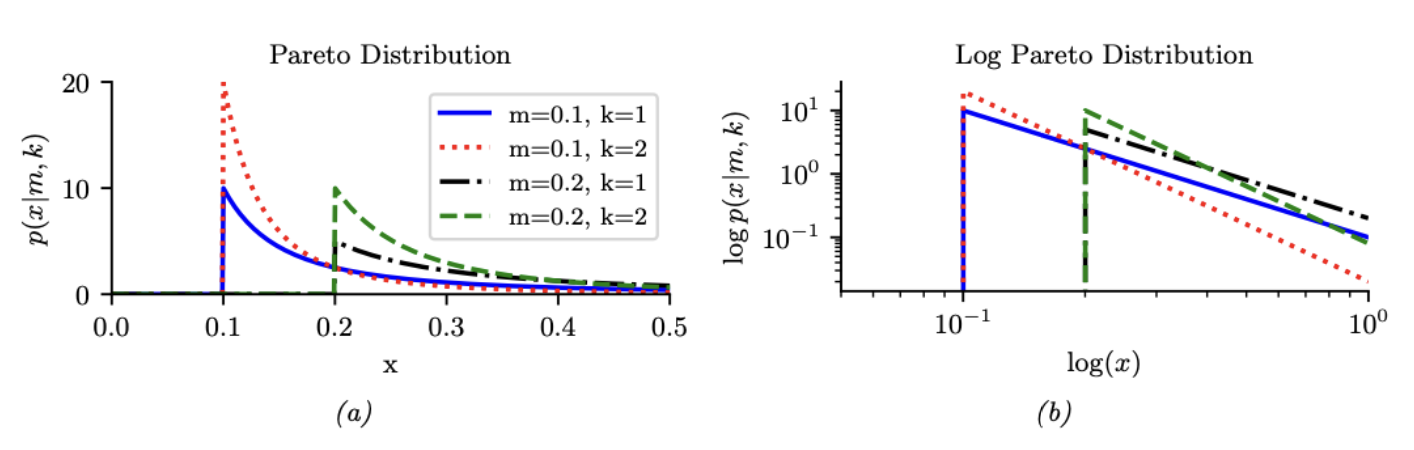
图 $2.4$：（a）帕累托pdf $\operatorname{Pareto}(x \mid k, m)$。（b）对数图上的分布。

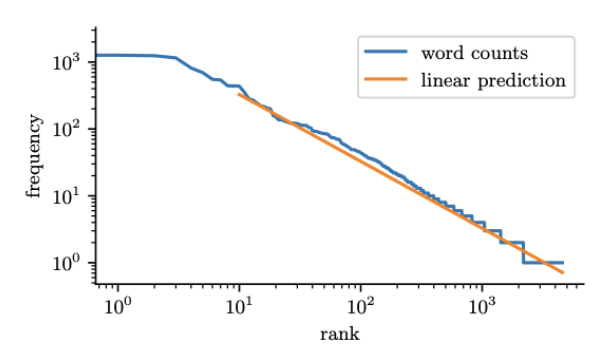
图 $2.5$：H.G.Wells的《时间机器》中单词的频率与排名的对数图。由zipfs_law_plot.ipynb生成。改编自[Zha+20a，第8.3节]中的数字。

2.2.3.5 帕累托分布（Pareto Distribution）

帕累托分布（Pareto distribution）具有以下概率密度函数（pdf）：

\[\operatorname{Pareto}(x \mid m, \kappa)=\kappa m^\kappa \frac{1}{x^{(\kappa+1)}} \mathbb{I}(x \geq m) \tag{2.46}\]

请参考图2.4(a)。我们可以看到 $x$ 必须大于最小值 $m$，但之后 pdf 迅速衰减。如果我们在对数-对数尺度上绘制这个分布，它会形成一条直线 $\log p(x) = -\alpha \log x + \log(c)$，其中 $\alpha = \frac{1}{m}$ 且 $c = \alpha m$；请参考图2.4(b)。

当 $m = 0$，分布具有形式 $p(x) = \alpha x^{-\alpha}$。这被称为幂律分布（power law）。如果 $\alpha = 1$，分布具有形式 $p(x) \propto \frac{1}{x}$；如果我们将 $x$ 解释为频率，这被称为倒数函数 $1/f$。

帕累托分布适用于模拟重尾或长尾**的分布，在这些分布中，大多数值都很小，但有一些非常大的值。许多类型的数据都表现出这种特性。（[ACL16]⁷ 认为这是因为许多数据集是由多种潜在因素生成的，这些因素混合在一起时，自然会导致重尾分布。）下面我们给出一些例子。

模拟财富分布

帕累托分布是以意大利经济学家和社会学家维尔弗雷多·帕累托（Vilfredo Pareto）命名的，他创建这个分布是为了模拟不同国家财富的分布情况。实际上，在经济学中，参数 $\alpha$ 被称为帕累托指数（Pareto index）。如果我们设定 $\alpha = 1.16$，我们就得到了所谓的80-20规则，即社会中80%的财富被20%的人所持有。

Zipf定律

Zipf定律（Zipf’s law）表明，一种语言中出现频率最高的单词（例如“the”）大约是第二频繁单词（“of”）出现频率的两倍，而“of”出现频率又是第四频繁单词出现频率的两倍，以此类推。这对应于如下形式的帕累托分布：

\[p(x=r) \propto \kappa r^{-a} \tag{2.47}\]

其中 $r$ 是按照频率排序的单词 $x$ 的排名，$\alpha$ 和 $a$ 是常数。如果我们设定 $a = 1$，我们就得到了Zipf定律。因此，Zipf定律预测，如果我们绘制单词的对数频率与它们的对数排名的图，我们将得到一条斜率为 $-1$ 的直线。实际上确实如此，如图2.5.4所示。有关Zipf定律的进一步讨论，请参阅[Ada00]⁸，以及第2.6.2节中关于语言模型的讨论。

2.2.4 0-1区间上的连续分布

在这一部分，我们讨论一些定义在[0, 1]区间上的单变量分布。

2.2.4.1 Beta分布

贝塔分布（Beta distribution）是其中一种分布，其在区间[0, 1]上有定义，并且定义如下：

\[\operatorname{Beta}(x \mid a, b)=\frac{1}{B(a, b)} x^{a-1}(1-x)^{b-1} \tag{2.48}\]

其中 $B(\alpha, \beta)$ 是贝塔函数。我们需要 $\alpha > 0$ 和 $\beta > 0$ 来确保分布是可积的（即确保 $B(\alpha, \beta)$ 存在）。如果 $\alpha = \beta = 1$，我们得到的是均匀分布。如果 $\alpha$ 和 $\beta$ 都小于1，我们得到一个在0和1处有“尖峰”的双峰分布；如果 $\alpha$ 和 $\beta$ 都大于1，分布是单峰的。请参考图2.3b。

2.2.5 多变量连续分布

在这一部分，我们总结了一些其他广泛使用的多变量连续分布。

2.2.5.1 多变量正态分布（高斯分布）

多变量正态分布（multivariate normal，MVN），也称为多变量高斯分布，是迄今为止最广泛使用的多变量分布。因此，整个第2.3节都将专门讨论它。

2.2.5.2 多变量学生分布

高斯分布的一个问题是它们对异常值很敏感。幸运的是，我们可以很容易地将第2.2.2.3节中讨论的学生分布扩展到$D$维。多变量学生分布（multivariate Student distribution）的概率密度函数（pdf）由以下公式给出：

\[\begin{align} \mathcal{T}_\nu(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}) & =\frac{1}{Z}\left[1+\frac{1}{\nu}(x-\mu)^{\top} \Sigma^{-1}(x-\mu)\right]^{-\left(\frac{\nu+D}{2}\right)} \tag{2.49}\\ Z & =\frac{\Gamma(\nu / 2)}{\Gamma(\nu / 2+D / 2)} \frac{\nu^{D / 2} \pi^{D / 2}}{|\boldsymbol{\Sigma}|^{-1 / 2}} \tag{2.50} \end{align}\]

其中$\mathbf{\Sigma}$ 是缩放矩阵。

学生t分布的尾部比高斯分布更厚。$\nu$（自由度）越小，尾部越厚。当 $\nu \to \infty$，分布趋向于高斯分布。该分布具有以下性质：

\[\text { mean }=\mu, \text { mode }=\mu, \operatorname{cov}=\frac{\nu}{\nu-2} \Sigma \tag{2.51}\]

均值仅在 $\nu > 1$ 时有定义（有限）。同样，协方差仅在 $\nu > 2$ 时有定义。

2.2.5.3 圆形正态分布（也称为冯·米塞斯分布，von Mises Fisher分布）

有时数据分布于单位球面上，而不是欧几里得空间中的任意点。例如，任何被“2-归一化”的$D$ 维向量都嵌入在 $\mathbb{R}^D$ 空间中的单位 $(D-1)$ 球面上。

还有一个适合这类角度数据的衍生高斯分布，被称为冯·米塞斯-费舍尔（von Mises-Fisher）分布，或称圆形正态（circular normal）分布。它的概率密度函数（pdf）如下：

\[\begin{align} \operatorname{vMF}(\boldsymbol{x} \mid \boldsymbol{\mu}, \kappa) & \triangleq \frac{1}{Z} \exp \left(\kappa \boldsymbol{\mu}^{\top} \boldsymbol{x}\right) \tag{2.52}\\ Z & =\frac{(2 \pi)^{D / 2} I_{D / 2-1}(\kappa)}{\kappa^{D / 2-1}} \tag{2.53} \end{align}\]

其中 $ \boldsymbol{\mu} $ 是均值（满足 $ \lvert \mu \rvert = 1 $），$ \kappa \geq 0 $ 是集中度或精确度参数（类似于标准高斯分布中的 $ \frac{1}{\sigma} $），$ Z $ 是归一化常数，$ I_r(\kappa) $ 是第一类修正贝塞尔函数，阶数为 $ r $。冯·米塞斯-费舍尔分布类似于球面多变量高斯分布，它的参数化是基于余弦距离而不是欧几里得距离。

冯·米塞斯-费舍尔（vMF）分布可以在混合模型中使用，用于聚类“2-归一化”向量，作为使用高斯混合模型的替代方案[Ban+05][^Ban05]。如果 $ \kappa \to 0 $，这会简化为球面$\text{K-means}$算法。它还可以在混合模型（主要部分$28.4.2$）中使用；这被称为球面主题模型[Rei+10]⁹。

如果 $ D = 2 $，另一种选择是使用单位圆上的冯·米塞斯（von Mises）分布，其形式为：

\[\begin{align} \operatorname{vMF}(x \mid \mu, \kappa) & =\frac{1}{Z} \exp (\kappa \cos (x-\mu)) \tag{2.54}\\ Z & =2 \pi I_0(\kappa) \tag{2.55} \end{align}\]

2.2.5.4 矩阵正态分布（Matrix Normal Distribution，简称MN ）

矩阵正态（matrix normal）分布是由以下概率密度函数定义的，适用于矩阵随机变量 $\mathbf{X} \in \mathbb{R}^{n \times p}$：

\[\mathcal{M N}(\mathbf{X} \mid \mathbf{M}, \mathbf{U}, \mathbf{V}) \triangleq \frac{|\mathbf{V}|^{n / 2}}{2 \pi^{n p / 2}|\mathbf{U}|^{p / 2}} \exp \left\{-\frac{1}{2} \operatorname{tr}\left[(\mathbf{X}-\mathbf{M})^{\boldsymbol{\top}} \mathbf{U}^{-1}(\mathbf{X}-\mathbf{M}) \mathbf{V}\right]\right\} \tag{2.56}\]

其中 $\mathbf{M} \in \mathbb{R}^{n \times p}$ 是 $\mathbf{X}$ 的均值矩阵，$\mathbf{U} \in \mathbb{S}_{n \times n}^{++}$ 是行与行之间的协方差矩阵，$\mathbf{V} \in \mathbb{S}_{p \times p}^{++}$ 是列与列之间的精度矩阵。可以看出，

\[\operatorname{vec}(\mathbf{X}) \sim \mathcal{N}\left(\operatorname{vec}(\mathbf{M}), \mathbf{V}^{-1} \otimes \mathbf{U}\right) \tag{2.57}\]

请注意，矩阵正态分布的定义还有另一个版本，它使用列协方差矩阵 $ \tilde{\mathbf{V}} = \mathbf{V}^{-1} $ 而不是 $ \mathbf{V} $，这会导致密度函数有所不同。

\[\frac{1}{2 \pi^{n p / 2}|\mathbf{U}|^{p / 2}|\tilde{\mathbf{V}}|^{n / 2}} \exp \left\{-\frac{1}{2} \operatorname{tr}\left[(\mathbf{X}-\mathbf{M})^{\top} \mathbf{U}^{-1}(\mathbf{X}-\mathbf{M}) \tilde{\mathbf{V}}^{-1}\right]\right\} \tag{2.58}\]

这两个版本的矩阵正态分布定义显然是等价的，但我们将会看到，我们在方程（2.56）中采用的定义使得后验分布更加简洁（正如在分析具有共轭先验的多元正态分布的后验时，使用精度矩阵比使用协方差矩阵更为方便）。

2.2.5.5 约翰·威沙特分布（ Wishart distribution ）

Wishart分布是将伽马分布推广到正定矩阵的分布。Press [Pre05]¹⁰ 第107页曾说过，“在多元统计学中，Wishart分布在重要性和实用性方面仅次于正态分布”。我们将主要用它来模拟我们在估计协方差矩阵时的不确定性（见第3.4.4节）。

Wishart分布的概率密度函数（pdf）定义如下：

\[\begin{align} \mathrm{Wi}(\boldsymbol{\Sigma} \mid \mathbf{S}, \nu) & \triangleq \frac{1}{Z}|\Sigma|^{(\nu-D-1) / 2} \exp \left(-\frac{1}{2} \operatorname{tr}\left(\mathbf{S}^{-1} \boldsymbol{\Sigma}\right)\right) \tag{2.59}\\ Z & \triangleq|\mathbf{S}|^{-\nu / 2} 2^{\nu D / 2} \Gamma_D(\nu / 2) \tag{2.60} \end{align}\]

在这里，$\nu$ 被称为“自由度”，而 $\mathbf{S}$ 是“尺度矩阵”。（我们很快就会对这些参数有更多的直觉。）归一化常数仅在 $\nu > D - 1$ 时存在（因此，概率密度函数仅在这种情况下才被良好定义）。

该分布具有如下属性：

\[\text { mean }=\nu \mathbf{S}, \text { mode }=(\nu-D-1) \mathbf{S} \tag{2.61}\]

需要注意的是峰值只会在 $\nu>D+1$ 时存在。

如果 $D=1$，该分布将退化为伽马分布：

\[\mathrm{Wi}\left(\lambda \mid s^{-1}, \nu\right)=\mathrm{Ga}\left(\lambda \mid \text { shape }=\frac{\nu}{2}, \text { rate }=\frac{1}{2 s}\right) \tag{2.62}\]

如果 $s=2$，该分布将退化为卡方分布。

Wishart分布和高斯分布之间有一个有趣的联系。具体而言，设 $\boldsymbol{x}_n \sim N(0, \boldsymbol{\Sigma})$。可以证明，scatter矩阵 $\mathbf{S} = \sum_{n=1}^{N} \boldsymbol{x}_n \boldsymbol{x}_n^T$ 服从Wishart分布：$\mathbf{S} \sim \text{Wi}(\boldsymbol{\Sigma}; N)$。

2.2.5.6 逆威沙特分布

如果 $ \lambda \sim \text{Ga}(a; b) $，那么 $\frac{1}{\lambda} \sim \text{IG}(a; b)$。类似地，如果 $\mathbf{\Sigma}^{-1} \sim \mathrm{Wi}\left(\mathbf{S}^{-1}, \nu\right)$ 那么 $\boldsymbol{\Sigma} \sim \operatorname{IW}(\mathbf{S}, \nu)$，其中 $\text{IW}$ 是逆Wishart分布，即逆伽马分布的多维推广。它定义如下，对于 $\nu > D - 1$ 且 $\mathbf{S} \succ 0$：

\[\begin{align} \operatorname{IW}\left(\boldsymbol{\Sigma} \mid \mathbf{S}^{-1}, \nu\right) & =\frac{1}{Z}|\mathbf{\Sigma}|^{-(\nu+D+1) / 2} \exp \left(-\frac{1}{2} \operatorname{tr}\left(\mathbf{S} \boldsymbol{\Sigma}^{-1}\right)\right) \tag{2.63}\\ Z_{\mathrm{IW}} & =|\mathbf{S}|^{\nu / 2} 2^{\nu D / 2} \Gamma_D(\nu / 2) \tag{2.64} \end{align}\]

可以证明该分布具有以下性质：

\[\text { mean }=\frac{\mathbf{S}}{\nu-D-1}, \text { mode }=\frac{\mathbf{S}}{\nu+D+1} \tag{2.65}\]

如果 $ D = 1 $，这将简化为逆伽马分布：

\[\operatorname{IW}\left(\sigma^2 \mid s^{-1}, \nu\right)=\operatorname{IG}\left(\sigma^2 \mid \nu / 2, s / 2\right) \tag{2.66}\]

如果 $ s = 1 $，这将简化为逆卡方分布。

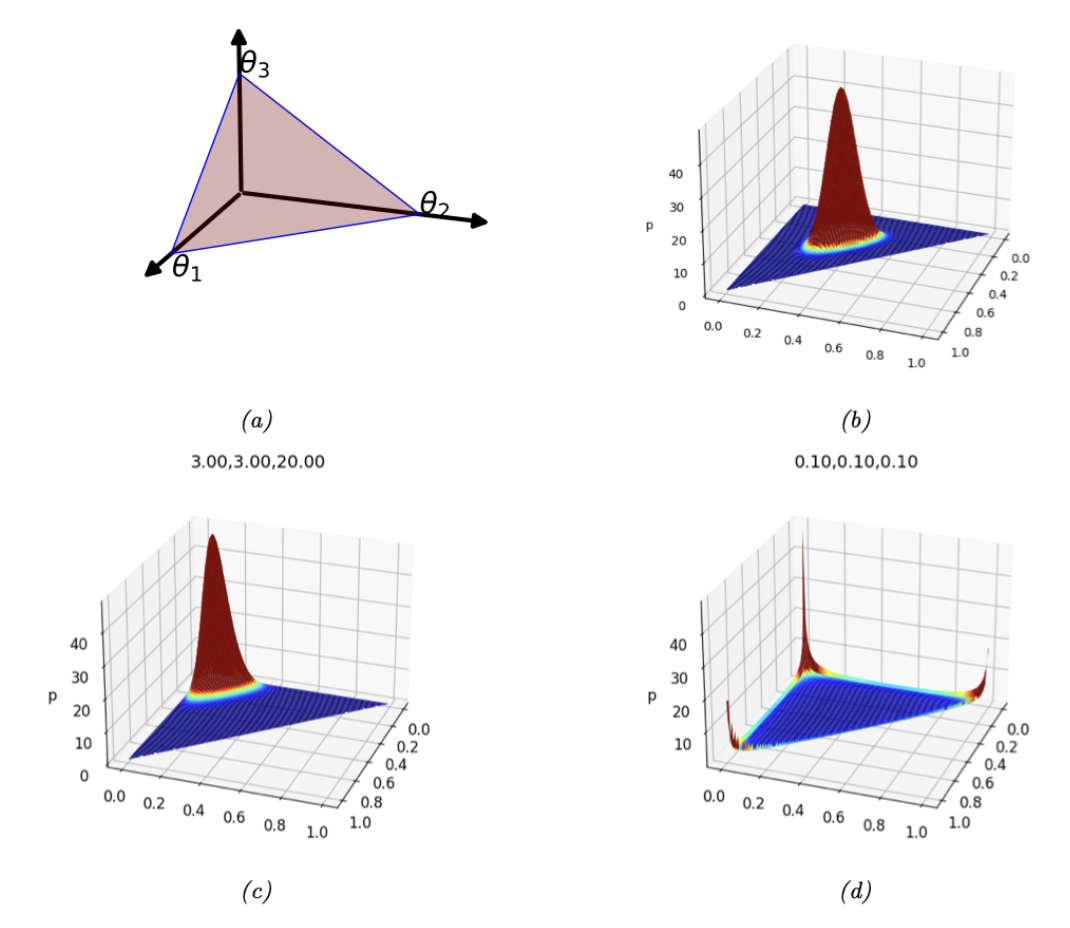
图 $2.6$：（a）当$K=3$时，狄利克雷分布定义了单纯形上的分布，可以用三角形曲面表示。该曲面上的点满足 $0 \leq \theta_c \leq 1$ 和 $\sum_{c=1}^3 \theta_c=1$。（b） $\boldsymbol{\alpha}=(20,20,20)$的狄利克雷密度图。（c） $\boldsymbol{\alpha}=(3,3,20)$的狄利克雷密度图。（d）$\boldsymbol{\alpha}=(0.1,0.1,0.1)$ 的狄利克雷密度图。

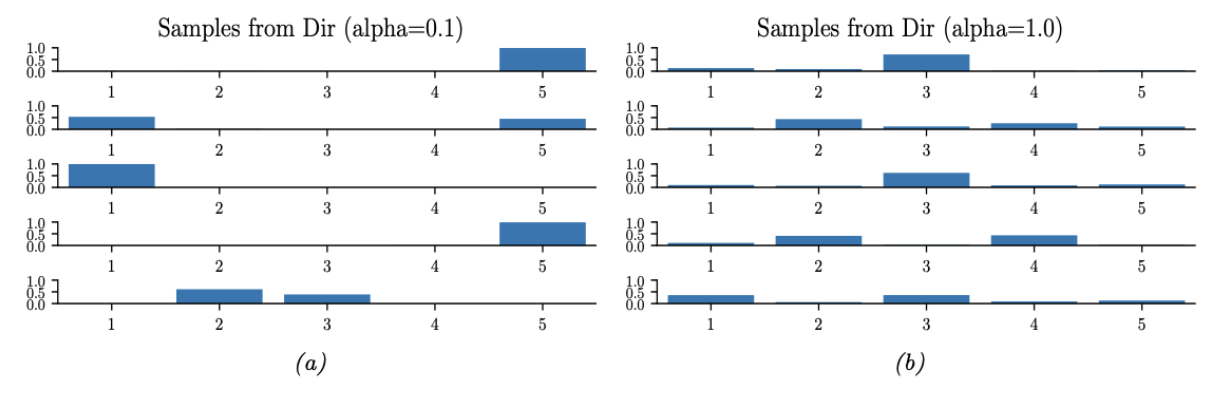
图 $2.7$：来自不同参数值的5维对称狄利克雷分布的样本。（a） $\boldsymbol{\alpha}=(0.1, \ldots, 0.1)$。这导致了非常稀疏的分布，有很多0。（b）$\boldsymbol{\alpha}=(1, \ldots, 1)$。这导致更均匀（和密集）的分布。

2.2.5.7 Dirichlet distribution

Dirichlet分布是Beta分布的多变量推广，其支撑集位于概率单纯形（probability simplex）上，定义为

\[S_K=\left\{\boldsymbol{x}: 0 \leq x_k \leq 1, \sum_{k=1}^K x_k=1\right\} \tag{2.67}\]

概率密度函数定义为：

\[\operatorname{Dir}(\boldsymbol{x} \mid \boldsymbol{\alpha}) \triangleq \frac{1}{B(\boldsymbol{\alpha})} \prod_{k=1}^K x_k^{\alpha_k-1} \mathbb{I}\left(\boldsymbol{x} \in S_K\right) \tag{2.68}\]

其中 $ B(\boldsymbol{\alpha}) $ 是多变量Beta函数，

\[B(\boldsymbol{\alpha}) \triangleq \frac{\prod_{k=1}^K \Gamma\left(\alpha_k\right)}{\Gamma\left(\sum_{k=1}^K \alpha_k\right)} \tag{2.69}\]

图2.6显示了当 $K = 3$ 时Dirichlet分布的一些图形。我们可以看到 $\alpha_0 = \sum_{k} \alpha_k$ 控制分布的强度（它有多峰值），而 $\alpha_k$ 控制峰值的位置。例如，$\text{Dir}(1; 1; 1)$ 是一个均匀分布，$\text{Dir}(2; 2; 2)$ 是一个以 $\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$ 为中心的宽分布，$\text{Dir}(20; 20; 20)$ 是一个以 $\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$ 为中心的窄分布。$\text{Dir}(3; 3; 20)$ 是一个不对称分布，它在一个角上有更多的密度。如果对于所有 $k$，$\alpha_k < 1$，我们会在单纯形的角上得到“尖刺”。当 $\alpha_k < 1$ 时，从分布中抽取的样本是稀疏的，如图2.7所示。

以供将来参考，以下是Dirichlet分布的一些有用性质：

\[\mathbb{E}\left[x_k\right]=\frac{\alpha_k}{\alpha_0}, \operatorname{mode}\left[x_k\right]=\frac{\alpha_k-1}{\alpha_0-K}, \mathbb{V}\left[x_k\right]=\frac{\alpha_k\left(\alpha_0-\alpha_k\right)}{\alpha_0^2\left(\alpha_0+1\right)} \tag{2.70}\]

其中 $\alpha_0=\sum_k \alpha_k$。

通常我们使用形式为 $\alpha_k = \alpha = \frac{1}{K}$ 的对称Dirichlet先验。在这种情况下，我们有 $\mathbb{E}[x_k] = \frac{1}{K}$，并且 $\mathbb{V}[x_k] = \frac{K-1}{K^2(\alpha+1)}$。因此，我们可以看到增加 $\alpha$ 会增加分布的精度（减少方差）。

Dirichlet分布有助于区分偶然性（数据）不确定性和认知不确定性。为了理解这一点，考虑一个三面的骰子。如果我们知道每个结果出现的可能性是相等的，我们可以使用一个“尖锐”的对称Dirichlet分布，比如图2.6(b)中显示的$\text{Dir}(20; 20; 20)$；这反映了我们确信结果将是不可预测的。相比之下，如果我们不确定结果会是什么样子（例如，它可能是一个有偏的骰子），那么我们可以使用一个“平坦”的对称Dirichlet分布，比如$\text{Dir}(1; 1; 1)$，它可以生成一系列可能的结果分布。我们可以使Dirichlet分布依赖于输入，从而形成所谓的先验网络（prior network）[MG18]¹¹，因为它编码的是$p(\theta \mid x)$（输出是一个分布）而不是$p(y \mid x)$（输出是一个标签）。

2.3 高斯联合分布

连续随机变量中最常用的联合概率分布是多元高斯分布或多元正态分布（MVN）。这种分布之所以流行，部分原因是它在数学上很方便，更多是因为高斯分布假设在许多情况下是相当合理的。实际上，高斯分布是在给定一阶矩和二阶矩的情况下具有最大熵的分布（第2.4.7节）。鉴于其重要性，本节将详细讨论高斯分布。

2.3.1 多变量正态分布

在本节中，我们将详细讨论多元高斯分布或多元正态分布。

2.3.1.1 定义

MVN定义为：

\[\mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}) \triangleq \frac{1}{(2 \pi)^{D / 2}|\boldsymbol{\Sigma}|^{1 / 2}} \exp \left[-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right] \tag{2.71}\]

其中 $\boldsymbol{\mu}=\mathbb{E}[\boldsymbol{x}] \in \mathbb{R}^D$ 表示均值向量，而 $\boldsymbol{\Sigma} = \text{Cov}[\boldsymbol{x}]$ 表示大小为 $D \times D$ 的协方差矩阵。归一化常数 $Z = (2\pi)^{D/2}\lvert\boldsymbol{\Sigma}\rvert^{-1/2}$ 确保概率密度函数（pdf）的积分为 1。指数内的表达式（忽略 $-0.5$ 因子）是数据向量 $\boldsymbol{x}$ 和均值向量 $\boldsymbol{\mu}$ 之间的平方马氏距离（Mahalanobis distance），由以下公式给出：

\[d_{\boldsymbol{\Sigma}}(\boldsymbol{x}, \boldsymbol{\mu})^2=(\boldsymbol{x}-\boldsymbol{\mu})^{\top} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) \tag{2.72}\]

在二维情况下，多元正态分布（MVN）被称为二元高斯分布。其概率密度函数可以表示为 $\boldsymbol{x} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$，其中 $\boldsymbol{x} \in \mathbb{R}^2$，$\boldsymbol{\mu} \in \mathbb{R}^2$，以及 $\boldsymbol{\Sigma}$ 是一个 $2 \times 2$ 的协方差矩阵。

\[\boldsymbol{\Sigma}=\left(\begin{array}{cc} \sigma_1^2 & \sigma_{12}^2 \\ \sigma_{21}^2 & \sigma_2^2 \end{array}\right)=\left(\begin{array}{cc} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{array}\right) \tag{2.73}\]

其中相关系数为 $\rho \triangleq \frac{\sigma_{12}^2}{\sigma_1 \sigma_2}$。

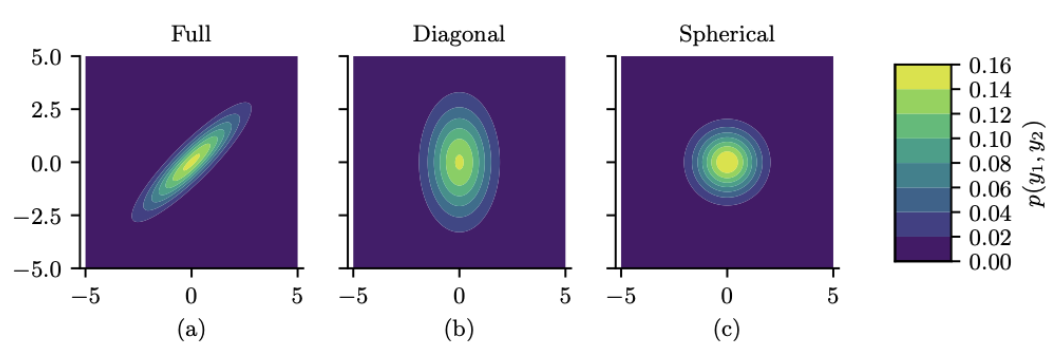
图 $2.8$：二维高斯密度等高线的可视化。（a）全协方差矩阵具有椭圆轮廓。（b）对角协方差矩阵是一个轴对齐的椭圆。（c）球面协方差矩阵具有圆形形状。

图 2.8 展示了二维情况下三种不同协方差矩阵对应的多元正态分布密度等高线图。一个完整的协方差矩阵有 $D(D + 1)/2$ 个参数，其中我们除以 2 是因为 $\boldsymbol{\Sigma}$ 是对称的。一个对角协方差矩阵（diagonal covariance matrix）有 $D$ 个参数，并且在非对角线上的项为 0。一个球形协方差矩阵（spherical covariance matrix），也称为各向同性协方差矩阵（isotropic covariance matrix），其形式为 $\Sigma = \sigma^2 \mathbf{I}_D$，因此它只有一个自由参数，即 $\sigma^2$。

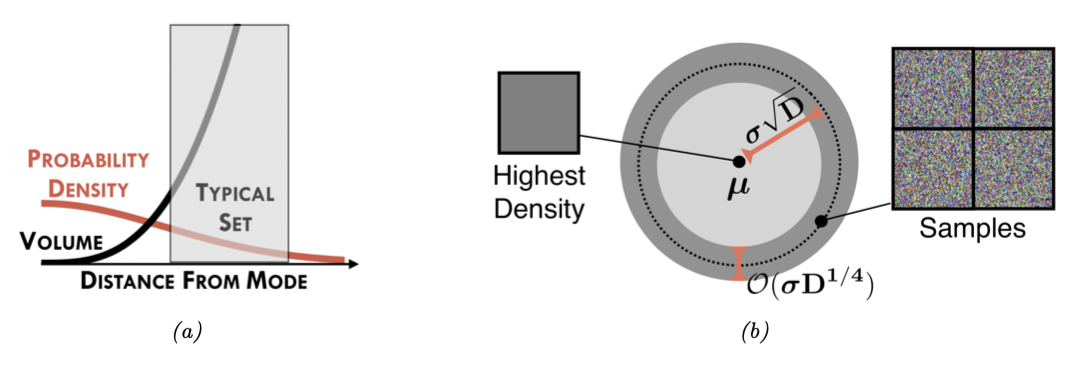
图 $2.9$：（a）为什么高斯分布的典型集合不以分布模式为中心。（b）高斯分布的典型集合的图示，该集合集中在厚度为 $\sigma D^{1 / 4}$ 、距离原点为 $\sigma D^{1 / 2}$ 的薄环中。我们还显示了密度最高的图像（左侧的全灰色图像）。以及一些高概率样本（右侧的斑点噪声图像）。从[Nal+19a]¹²的图1中可以看出。在Eric Nalisnick的善意许可下使用。

2.3.1.2 Gaussian shells

在高维空间中，多元高斯分布的行为可能相当反直觉。具体来说，我们可以提出这样的问题：如果我们抽取样本 $\boldsymbol{x} \sim \mathcal{N}\left(\mathbf{0}, \mathbf{I}_D\right)$，其中 $D$ 表示数据的维度，我们预期的大多数样本 $\boldsymbol{x}$ 分布在什么区域呢？由于概率密度函数（pdf）的峰值（众数）处在原点，很自然地会期望大多数样本分布在原点附近。然而，在高维空间中，高斯分布的典型集合（Typical Set）是一个薄壳或环带，其距离原点的距离为 $r = \sigma\sqrt{D}$ ，厚度为 $O(\sigma D^{1/4})$。

这种现象的直观原因是：尽管密度以 $e^{-r^2/2}$ 的速度衰减——意味着密度从原点开始减少，但球体的体积以 $r^D$ 的速度增长——意味着体积从原点开始增加，并且由于质量是密度乘以体积，所以大多数点最终会落在这个环带区域——密度和体积在这里达到“平衡”。这被称为“高斯肥皂泡”（Gaussian soap bubble）现象，如图 2.9 所示。

为了理解为什么高斯分布的典型集合集中在半径为 $\sqrt{D}$ 的薄环带中，考虑一个样本 $\boldsymbol{x}$ 到原点的距离 $d(\boldsymbol{x}) = \sqrt{\sum_{i=1}^D x_i^2}$，其中 $x_i \sim \mathcal{N}(0; 1)$。平方距离的期望为 $\mathbb{E}\left[d^2\right]=\sum_{i=1}^D \mathbb{E}\left[x_i^2\right]=D$ ，平方距离的方差为 $\mathbb{V}\left[d^2\right]=\sum_{i=1}^D \mathbb{V}\left[x_i^2\right]=D$ 。随着 $D$ 的增长，变异系数（即标准差相对于均值）趋向于零：

\[\lim _{D \rightarrow \infty} \frac{\operatorname{std}\left[d^2\right]}{\mathbb{E}\left[d^2\right]}=\lim _{D \rightarrow \infty} \frac{\sqrt{D}}{D}=0 \tag{2.74}\]

因此，平方距离的期望集中在 $D$ 附近，所以距离的期望集中在 $\mathbb{E}[d(\boldsymbol{x})]=\sqrt{D}$ 附近。更严格的证明见[Ver18]¹³，关于典型集合的讨论见第5.2.3节。

为了理解这在图像场景中的含义，在图2.9b中，我们展示了一些从高斯分布 $\mathcal{N}\left(\boldsymbol{\mu}, \sigma^2 \mathbf{I}\right)$ 中采样的灰度图像，其中 $\boldsymbol{\mu}$ 对应于全灰图像。然而，正如图中所示，随机采样的图像非常不像灰度图像，言下之意，大部分样本并非集中在期望附近。

2.3.1.3 MVN的边际分布和条件分布

让我们将随机变量向量 $\boldsymbol{x}$ 拆分成两个部分 $\boldsymbol{x}_1$ 和 $\boldsymbol{x}_2$，这样

\[\boldsymbol{\mu}=\binom{\boldsymbol{\mu}_1}{\boldsymbol{\mu}_2}, \quad \boldsymbol{\Sigma}=\left(\begin{array}{ll} \boldsymbol{\Sigma}_{11} & \boldsymbol{\Sigma}_{12} \\ \boldsymbol{\Sigma}_{21} & \boldsymbol{\Sigma}_{22} \end{array}\right) \tag{2.75}\]

这个分布的边缘分布如下（证明见第2.3.1.5节）：

\[\begin{align} & p\left(\boldsymbol{x}_1\right)=\int \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}) d \boldsymbol{x}_2 \triangleq \mathcal{N}\left(\boldsymbol{x}_1 \mid \boldsymbol{\mu}_1^m, \boldsymbol{\Sigma}_1^m\right)=\mathcal{N}\left(\boldsymbol{x}_1 \mid \boldsymbol{\mu}_1, \boldsymbol{\Sigma}_{11}\right) \tag{2.76}\\ & p\left(\boldsymbol{x}_2\right)=\int \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}) d \boldsymbol{x}_1 \triangleq \mathcal{N}\left(\boldsymbol{x}_2 \mid \boldsymbol{\mu}_2^m, \boldsymbol{\Sigma}_2^m\right)=\mathcal{N}\left(\boldsymbol{x}_2 \mid \boldsymbol{\mu}_2, \boldsymbol{\Sigma}_{22}\right) \tag{2.77} \end{align}\]

条件分布可以证明具有以下形式（证明见第2.3.1.5节）：

\[\begin{align} & p\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_2\right)=\mathcal{N}\left(\boldsymbol{x}_1 \mid \boldsymbol{\mu}_{1 \mid 2}^c, \boldsymbol{\Sigma}_{1 \mid 2}^c\right)=\mathcal{N}\left(\boldsymbol{x}_1 \mid \boldsymbol{\mu}_1+\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1}\left(\boldsymbol{x}_2-\boldsymbol{\mu}_2\right), \boldsymbol{\Sigma}_{11}-\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1} \boldsymbol{\Sigma}_{21}\right) \tag{2.78}\\ & p\left(\boldsymbol{x}_2 \mid \boldsymbol{x}_1\right)=\mathcal{N}\left(\boldsymbol{x}_2 \mid \boldsymbol{\mu}_{2 \mid 1}^c, \boldsymbol{\Sigma}_{2 \mid 1}^c\right)=\mathcal{N}\left(\boldsymbol{x}_2 \mid \boldsymbol{\mu}_2+\boldsymbol{\Sigma}_{21} \boldsymbol{\Sigma}_{11}^{-1}\left(\boldsymbol{x}_1-\boldsymbol{\mu}_1\right), \boldsymbol{\Sigma}_{22}-\boldsymbol{\Sigma}_{21} \boldsymbol{\Sigma}_{11}^{-1} \boldsymbol{\Sigma}_{12}\right) \tag{2.79} \end{align}\]

需要注意的是，条件分布 $p(\boldsymbol{x}_1 \mid \boldsymbol{x}_2)$ 的均值是关于 $\boldsymbol{x}_2$ 的线性函数，但协方差与 $\boldsymbol{x}_2$ 本身无关，这是高斯分布的一个特殊性质。

2.3.1.4 Information(canonical) 形式

通常，我们用均值向量 $\boldsymbol{\mu}$ 和协方差矩阵 $\boldsymbol{\Sigma}$ 来参数化多变量正态分布（MVN）。然而，正如第2.4.2.5节所解释的，有时使用规范参数（canonical parameters）或自然参数（natural parameters）来表示高斯分布会更方便，这些参数定义为：

\[\boldsymbol{\Lambda} \triangleq \boldsymbol{\Sigma}^{-1}, \quad \boldsymbol{\eta} \triangleq \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu} \tag{2.80}\]

矩阵 $\mathbf{\Lambda}=\mathbf{\Sigma}^{-1}$ 被称为 精度矩阵（precision matrix），向量 $\boldsymbol{\eta}$ 被称为 精度加权期望 (precision-weighted mean)。我们可以转换回更熟悉的 矩参数（moment parameters）的形式：

\[\boldsymbol{\mu}=\boldsymbol{\Lambda}^{-1} \boldsymbol{\eta}, \quad \boldsymbol{\Sigma}=\boldsymbol{\Lambda}^{-1} \tag{2.81}\]

所以我们可以将 MVN 写成 canonical 形式（又被称为 information 形式）：

\[\begin{align} & \mathcal{N}_c(\boldsymbol{x} \mid \boldsymbol{\eta}, \boldsymbol{\Lambda}) \triangleq c \exp \left(\boldsymbol{x}^{\top} \boldsymbol{\eta}-\frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{\Lambda} \boldsymbol{x}\right) \tag{2.82}\\ & c \triangleq \frac{\exp \left(-\frac{1}{2} \boldsymbol{\eta}^{\top} \boldsymbol{\Lambda}^{-1} \boldsymbol{\eta}\right)}{(2 \pi)^{D / 2} \sqrt{\operatorname{det}\left(\boldsymbol{\Lambda}^{-1}\right)}} \tag{2.83} \end{align}\]

其中我们使用符号 $\mathcal{N}_c()$ 来与标准化的 $\mathcal{N}()$ 做区分。了解更多关于矩参数和自然参数的内容，参考 2.4.2.5 节。

在 information 形式下，我们依然可以推导出边际分布和条件分布的形式（过程参考 2.3.1.6 节）。边际分布为

\[\begin{align} & p\left(\boldsymbol{x}_1\right)=\mathcal{N}_c\left(\boldsymbol{x}_1 \mid \boldsymbol{\eta}_1^m, \boldsymbol{\Lambda}_1^m\right)=\mathcal{N}_c\left(\boldsymbol{x}_1 \mid \boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{\Lambda}_{22}^{-1} \boldsymbol{\eta}_2, \boldsymbol{\Lambda}_{11}-\boldsymbol{\Lambda}_{12} \boldsymbol{\Lambda}_{22}^{-1} \boldsymbol{\Lambda}_{21}\right) \tag{2.84}\\ & p\left(\boldsymbol{x}_2\right)=\mathcal{N}_c\left(\boldsymbol{x}_2 \mid \boldsymbol{\eta}_2^m, \boldsymbol{\Lambda}_2^m\right)=\mathcal{N}_c\left(\boldsymbol{x}_2 \mid \boldsymbol{\eta}_2-\boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\eta}_1, \boldsymbol{\Lambda}_{22}-\boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\Lambda}_{12}\right) \tag{2.85} \end{align}\]

条件分布为

\[\begin{align} & p\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_2\right)=\mathcal{N}_c\left(\boldsymbol{x}_1 \mid \boldsymbol{\eta}_{1 \mid 2}^c, \boldsymbol{\Lambda}_{1 \mid 2}^c\right)=\mathcal{N}_c\left(\boldsymbol{x}_1 \mid \boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2, \boldsymbol{\Lambda}_{11}\right) \tag{2.86}\\ & p\left(\boldsymbol{x}_2 \mid \boldsymbol{x}_1\right)=\mathcal{N}_c\left(\boldsymbol{x}_2 \mid \boldsymbol{\eta}_{2 \mid 1}^c, \boldsymbol{\Lambda}_{2 \mid 1}^c\right)=\mathcal{N}_c\left(\boldsymbol{x}_2 \mid \boldsymbol{\eta}_2-\boldsymbol{\Lambda}_{21} \boldsymbol{x}_1, \boldsymbol{\Lambda}_{22}\right) \tag{2.87} \end{align}\]

我们可以发现边际分布在矩形式下更简单，条件分布在information形式下更简单。

2.3.1.5 推导：矩形式

本节，我们将介绍MVN在矩形式下边际分布（式2.77）和条件分布（式2.78）的推导。

在深入之前，我们需要引入如下的结论，对于一个分块矩阵

\[\mathbf{M}=\left(\begin{array}{ll} \mathbf{E} & \mathbf{F} \\ \mathbf{G} & \mathbf{H} \end{array}\right) \tag{2.88}\]

其中我们假设 $\mathbf{E}$ 和 $\mathbf{H}$ 是可逆的。可以证明它的逆矩阵是（参考[Mur22][^Mur22] 7.3.2节）

\[\begin{align} \mathbf{M}^{-1} & =\left(\begin{array}{cc} (\mathbf{M} / \mathbf{H})^{-1} & -(\mathbf{M} / \mathbf{H})^{-1} \mathbf{F} \mathbf{H}^{-1} \\ -\mathbf{H}^{-1} \mathbf{G}(\mathbf{M} / \mathbf{H})^{-1} & \mathbf{H}^{-1}+\mathbf{H}^{-1} \mathbf{G}(\mathbf{M} / \mathbf{H})^{-1} \mathbf{F H}^{-1} \end{array}\right) \tag{2.89}\\ & =\left(\begin{array}{cc} \mathbf{E}^{-1}+\mathbf{E}^{-1} \mathbf{F}(\mathbf{M} / \mathbf{E})^{-1} \mathbf{G E}^{-1} & -\mathbf{E}^{-1} \mathbf{F}(\mathbf{M} / \mathbf{E})^{-1} \\ -(\mathbf{M} / \mathbf{E})^{-1} \mathbf{G} \mathbf{E}^{-1} & (\mathbf{M} / \mathbf{E})^{-1} \end{array}\right) \tag{2.90} \end{align}\]

其中

\[\begin{align} & \mathbf{M} / \mathbf{H} \triangleq \mathbf{E}-\mathbf{F} \mathbf{H}^{-1} \mathbf{G} \tag{2.91}\\ & \mathbf{M} / \mathbf{E} \triangleq \mathbf{H}-\mathbf{G E}^{-1} \mathbf{F} \tag{2.92} \end{align}\]

我们称 $\mathbf{M}/\mathbf{H}$ 是 $\mathbf{M}$ 关于 $\mathbf{H}$ 的 Schur complement。$\mathbf{M}/\mathbf{E}$ 同理。

根据上式，我们有如下重要的结论，被称为 matrix inversion lemma 或者 Sherman-Morrison-Woodbury formula：

\[(\mathbf{M} / \mathbf{H})^{-1}=\left(\mathbf{E}-\mathbf{F} \mathbf{H}^{-1} \mathbf{G}\right)^{-1}=\mathbf{E}^{-1}+\mathbf{E}^{-1} \mathbf{F}\left(\mathbf{H}-\mathbf{G E}^{-1} \mathbf{F}\right)^{-1} \mathbf{G E}^{-1} \tag{2.93}\]

现在我们可以回到 MVN 条件分布公式的推导，首先将联合概率分布 $p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)$ 因式分解为 $p\left(\boldsymbol{x}_2\right) p\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_2\right)$ 的形式：

\[p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right) \propto \exp \left\{-\frac{1}{2}\binom{\boldsymbol{x}_1-\boldsymbol{\mu}_1}{\boldsymbol{x}_2-\boldsymbol{\mu}_2}^{\top}\left(\begin{array}{ll} \boldsymbol{\Sigma}_{11} & \boldsymbol{\Sigma}_{12} \\ \boldsymbol{\Sigma}_{21} & \boldsymbol{\Sigma}_{22} \end{array}\right)^{-1}\binom{\boldsymbol{x}_1-\boldsymbol{\mu}_1}{\boldsymbol{x}_2-\boldsymbol{\mu}_2}\right\} \tag{2.94}\]

使用块结构矩阵的逆方程，上述指数变为：

\[\begin{align} p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right) & \propto \exp \left\{-\frac{1}{2}\binom{\boldsymbol{x}_1-\boldsymbol{\mu}_1}{\boldsymbol{x}_2-\boldsymbol{\mu}_2}^{\top}\left(\begin{array}{cc} \mathbf{I} & \mathbf{0} \tag{2.95}\\ -\boldsymbol{\Sigma}_{22}^{-1} \boldsymbol{\Sigma}_{21} & \mathbf{I} \end{array}\right)\left(\begin{array}{cc} \left(\boldsymbol{\Sigma} / \boldsymbol{\Sigma}_{22}\right)^{-1} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{\Sigma}_{22}^{-1} \end{array}\right)\right. \\ & \left.\times\left(\begin{array}{cc} \mathbf{I} & -\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1} \\ \mathbf{0} & \mathbf{I} \end{array}\right)\binom{\boldsymbol{x}_1-\boldsymbol{\mu}_1}{\boldsymbol{x}_2-\boldsymbol{\mu}_2}\right\} \tag{2.96}\\ = & \exp \left\{-\frac{1}{2}\left(\boldsymbol{x}_1-\boldsymbol{\mu}_1-\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1}\left(\boldsymbol{x}_2-\boldsymbol{\mu}_2\right)\right)^{\top}\left(\boldsymbol{\Sigma} / \boldsymbol{\Sigma}_{22}\right)^{-1}\right. \tag{2.97}\\ & \left.\left(\boldsymbol{x}_1-\boldsymbol{\mu}_1-\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1}\left(\boldsymbol{x}_2-\boldsymbol{\mu}_2\right)\right)\right\} \times \exp \left\{-\frac{1}{2}\left(\boldsymbol{x}_2-\boldsymbol{\mu}_2\right)^{\top} \boldsymbol{\Sigma}_{22}^{-1}\left(\boldsymbol{x}_2-\boldsymbol{\mu}_2\right)\right\} \tag{2.98} \end{align}\]

上式的形式可以抽象为

\[\exp \left(\text { quadratic form in } \boldsymbol{x}_1, \boldsymbol{x}_2\right) \times \exp \left(\text { quadratic form in } \boldsymbol{x}_2\right) \tag{2.99}\]

因此，我们成功地将分布分解为：

\[\begin{align} p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right) & =p\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_2\right) p\left(\boldsymbol{x}_2\right) \tag{2.100}\\ & =\mathcal{N}\left(\boldsymbol{x}_1 \mid \boldsymbol{\mu}_{1 \mid 2}, \boldsymbol{\Sigma}_{1 \mid 2}\right) \mathcal{N}\left(\boldsymbol{x}_2 \mid \boldsymbol{\mu}_2, \boldsymbol{\Sigma}_{22}\right) \tag{2.101} \end{align}\]

其中

\[\begin{align} & \boldsymbol{\mu}_{1 \mid 2}=\boldsymbol{\mu}_1+\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1}\left(\boldsymbol{x}_2-\boldsymbol{\mu}_2\right) \tag{2.102}\\ & \boldsymbol{\Sigma}_{1 \mid 2}=\boldsymbol{\Sigma} / \boldsymbol{\Sigma}_{22} \triangleq \boldsymbol{\Sigma}_{11}-\boldsymbol{\Sigma}_{12} \boldsymbol{\Sigma}_{22}^{-1} \boldsymbol{\Sigma}_{21} \tag{2.103} \end{align}\]

其中 $\boldsymbol{\Sigma} / \boldsymbol{\Sigma}_{22}$ 表示 $\boldsymbol{\Sigma}$ 关于 $\boldsymbol{\Sigma}_{22}$ 的 Schur complement。

2.3.1.6 推导： information 形式

本节，我们将给出information 形式下 MVN 的边际分布和条件分布，即式（2.85）和（2.86）的证明。

首先考察条件分布。对参数进行分块：

\[\boldsymbol{\eta}=\binom{\boldsymbol{\eta}_1}{\boldsymbol{\eta}_2}, \quad \boldsymbol{\Lambda}=\left(\begin{array}{ll} \boldsymbol{\Lambda}_{11} & \boldsymbol{\Lambda}_{12} \\ \boldsymbol{\Lambda}_{21} & \boldsymbol{\Lambda}_{22} \end{array}\right) \tag{2.104}\]

现在我们可以将联合概率分布的对数写成：

\[\begin{align} \ln p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)= & -\frac{1}{2}\binom{\boldsymbol{x}_1}{\boldsymbol{x}_2}^{\top}\left(\begin{array}{cc} \boldsymbol{\Lambda}_{11} & \boldsymbol{\Lambda}_{12} \\ \boldsymbol{\Lambda}_{21} & \boldsymbol{\Lambda}_{22} \end{array}\right)\binom{\boldsymbol{x}_1}{\boldsymbol{x}_2}+\binom{\boldsymbol{x}_1}{\boldsymbol{x}_2}^{\top}\binom{\boldsymbol{\eta}_1}{\boldsymbol{\eta}_2}+\text { const. } \tag{2.105}\\ = & -\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{11} \boldsymbol{x}_1-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{22} \boldsymbol{x}_2-\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{12} \boldsymbol{x}_2-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{21} \boldsymbol{x}_1 \tag{2.106}\\ & +\boldsymbol{x}_1^{\top} \boldsymbol{\eta}_1+\boldsymbol{x}_2^{\top} \boldsymbol{\eta}_2+\text { const. } \tag{2.106} \end{align}\]

其中的常数项与 $\boldsymbol{x}_1$ 或 $\boldsymbol{x}_2$ 无关。

为了计算条件分布 $p\left(\boldsymbol{x}_1 \mid \boldsymbol{x}_2\right)$ 的参数，我们固定 $\boldsymbol{x}_2$ 的取值，并收集条件精度在 $\boldsymbol{x}_1$ 中为二次的项，然后收集条件精度加权平均值在 $\boldsymbol{x}_1$ 中呈线性的项。$\boldsymbol{x}_1$ 中的二次项仅为 $-\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{11} \boldsymbol{x}_1$，因此

\[\boldsymbol{\Lambda}_{1 \mid 2}^c=\boldsymbol{\Lambda}_{11} \tag{2.107}\]

在$\boldsymbol{x}_1$中呈线性的项是

\[-\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{12} \boldsymbol{x}_2-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{21} \boldsymbol{x}_1+\boldsymbol{x}_1^{\top} \boldsymbol{\eta}_1=\boldsymbol{x}_1^{\top}\left(\boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2\right) \tag{2.108}\]

考虑到 $\mathbf{\Lambda}_{21}^{\top}=\mathbf{\Lambda}_{12}$。所以条件精度加权期望为

\[\boldsymbol{\eta}_{1 \mid 2}^c=\boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2 \tag{2.109}\]

我们现在将以信息形式推导出边缘化的结果。边缘 $p\left(\boldsymbol{x}_2\right)$ 可以通过将关节 $p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)$ 与 $\boldsymbol{x}_1$ 积分来计算:

\[\begin{align} p\left(\boldsymbol{x}_2\right) & =\int p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right) d \boldsymbol{x}_1 \\ & \propto \int \exp \left\{-\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{11} \boldsymbol{x}_1-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{22} \boldsymbol{x}_2-\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{12} \boldsymbol{x}_2-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{21} \boldsymbol{x}_1+\boldsymbol{x}_1^{\top} \boldsymbol{\eta}_1+\boldsymbol{x}_2^{\top} \boldsymbol{\eta}_2\right\} d \boldsymbol{x}_1, \end{align}\]

其中指数中的项已被分解为方程（2.104）中的分区结构，如方程（2.106）中所示。接下来，收集涉及$\boldsymbol{x}_1$的所有术语，

\[p\left(\boldsymbol{x}_2\right) \propto \exp \left\{-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{22} \boldsymbol{x}_2+\boldsymbol{x}_2^{\top} \boldsymbol{\eta}_2\right\} \int \exp \left\{-\frac{1}{2} \boldsymbol{x}_1^{\top} \boldsymbol{\Lambda}_{11} \boldsymbol{x}_1+\boldsymbol{x}_1^{\top}\left(\boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2\right)\right\} d \boldsymbol{x}_1,\]

我们可以将被积函数识别为指数二次型。因此，积分等于高斯函数的归一化常数，精度为 $\boldsymbol{\Lambda}_{11}$，精度加权平均值为 $\boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2$，由方程（2.83）的倒数给出。将其代入我们的方程式，

\[\begin{align} p\left(\boldsymbol{x}_2\right) & \propto \exp \left\{-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{22} \boldsymbol{x}_2+\boldsymbol{x}_2^{\top} \boldsymbol{\eta}_2\right\} \exp \left\{\frac{1}{2}\left(\boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2\right)^{\top} \boldsymbol{\Lambda}_{11}^{-1}\left(\boldsymbol{\eta}_1-\boldsymbol{\Lambda}_{12} \boldsymbol{x}_2\right)\right\} \\ & \propto \exp \left\{-\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{22} \boldsymbol{x}_2+\boldsymbol{x}_2^{\top} \boldsymbol{\eta}_2+\frac{1}{2} \boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\Lambda}_{12} \boldsymbol{x}_2-\boldsymbol{x}_2^{\top} \boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\eta}_1\right\} \\ & =\exp \left\{-\frac{1}{2} \boldsymbol{x}_2^{\top}\left(\boldsymbol{\Lambda}_{22}-\boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\Lambda}_{12}\right) \boldsymbol{x}_2+\boldsymbol{x}_2^{\top}\left(\boldsymbol{\eta}_2-\boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\eta}_1\right)\right\} \end{align}\]

我们现在将其识别为$\boldsymbol{x}2$中的指数二次型。提取二次项以获得边际精度，

\[\boldsymbol{\Lambda}_{22}^m=\boldsymbol{\Lambda}_{22}-\boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\Lambda}_{12}, \tag{2.116}\]

以及获得边际精度加权平均值的线性项，

\[\boldsymbol{\eta}_2^m=\boldsymbol{\eta}_2-\boldsymbol{\Lambda}_{21} \boldsymbol{\Lambda}_{11}^{-1} \boldsymbol{\eta}_1 \tag{2.117}\]

2.3.2 线性高斯系统

考虑两个随机向量 $\boldsymbol{y} \in \mathbb{R}^D$ 和 $\boldsymbol{z} \in \mathbb{R}^L$，服从如下的分布关系：

\[\begin{align} p(\boldsymbol{z}) & =\mathcal{N}(\boldsymbol{z} \mid \breve{\mu}, \breve{\boldsymbol{\Sigma}}) \\ p(\boldsymbol{y} \mid \boldsymbol{z}) & =\mathcal{N}(\boldsymbol{y} \mid \mathbf{W} \boldsymbol{z}+\boldsymbol{b}, \boldsymbol{\Omega}) \end{align}\]

其中矩阵 $\mathbf{W}$ 大小为 $D\times L$。这是一个线性高斯系统（linear Gaussian system）的案例。

2.3.2.1 联合分布

联合概率分布 $p(\boldsymbol{z}, \boldsymbol{y})=p(\boldsymbol{z}) p(\boldsymbol{y} \mid \boldsymbol{z})$ 是一个 $D+L$ 维的高斯分布，期望和方差为（可以通过 moment匹配得到）：

\[\begin{align} p(\boldsymbol{z}, \boldsymbol{y}) & =\mathcal{N}(\boldsymbol{z}, \boldsymbol{y} \mid \tilde{\boldsymbol{\mu}}, \tilde{\mathbf{\Sigma}}) \tag{2.120a}\\ \tilde{\boldsymbol{\mu}} & \triangleq\binom{\breve{\boldsymbol{\mu}}}{\boldsymbol{m}} \triangleq\left(\begin{array}{cc} \breve{\boldsymbol{\mu}} \tag{2.120b}\\ \mathbf{W} \breve{\boldsymbol{\mu}}+\boldsymbol{b} \end{array}\right) \\ \tilde{\mathbf{\Sigma}} & \triangleq\left(\begin{array}{cc} \breve{\boldsymbol{\Sigma}} & \mathbf{C}^{\top} \\ \mathbf{C} & \mathbf{S} \end{array}\right) \triangleq\left(\begin{array}{cc} \breve{\mathbf{\Sigma}} & \breve{\mathbf{\Sigma}} \mathbf{W}^{\top} \\ \mathbf{W} \breve{\boldsymbol{\Sigma}} & \mathbf{W} \breve{\mathbf{\Sigma}} \mathbf{W}^{\top}+\boldsymbol{\Omega} \end{array}\right) \tag{2.120c} \end{align}\]

有关计算此联合分布的一些伪代码，请参阅第369页的算法8.1。

2.3.2.2 后验分布（高斯贝叶斯规则）

现在我们考虑从线性高斯系统计算后验分布 $p(\boldsymbol{z} \mid \boldsymbol{y})$。使用方程（2.78），我们发现后验分布由下式给出

\[\begin{align} p(\boldsymbol{z} \mid \boldsymbol{y}) & =\mathcal{N}(\boldsymbol{z} \mid \widehat{\boldsymbol{\mu}}, \widehat{\boldsymbol{\Sigma}}) \tag{2.121a}\\ \widehat{\boldsymbol{\mu}} & =\breve{\boldsymbol{\mu}}+\breve{\boldsymbol{\Sigma}} \mathbf{W}^{\boldsymbol{\top}}\left(\boldsymbol{\Omega}+\mathbf{W} \breve{\boldsymbol{\Sigma}} \mathbf{W}^{\boldsymbol{\top}}\right)^{-1}(\boldsymbol{y}-(\mathbf{W} \breve{\boldsymbol{\mu}}+\boldsymbol{b})) \tag{2.121b}\\ \widehat{\boldsymbol{\Sigma}} & =\breve{\boldsymbol{\Sigma}}-\breve{\boldsymbol{\Sigma}} \mathbf{W}^{\boldsymbol{\top}}\left(\boldsymbol{\Omega}+\mathbf{W} \breve{\boldsymbol{\Sigma}} \mathbf{W}^{\boldsymbol{\top}}\right)^{-1} \mathbf{W} \breve{\boldsymbol{\Sigma}}\tag{2.121c} \end{align}\]

这被称为高斯贝叶斯规则（Bayes’ rule for Gaussians）。我们看到，如果先验 $p(\boldsymbol{z})$ 是高斯分布，似然函数 $p(\boldsymbol{y} \mid \boldsymbol{z})$ 也是高斯分布，那么后验 $p(\boldsymbol{z} \mid \boldsymbol{y})$ 也会是高斯分布。因此，我们说高斯先验是高斯似然的共轭先验（conjugate prior），因为后验分布与先验具有相同的类型。（换句话说，高斯算子在贝叶斯更新下是封闭的。）

我们可以定义以下项来简化公式： $\mathbf{S}=\mathbf{W} \breve{\boldsymbol{\Sigma}} \mathbf{W}^{\top}+\boldsymbol{\Omega}, \mathbf{C}=\breve{\mathbf{\Sigma}} \mathbf{W}^{\top}$，$\boldsymbol{m}=\mathbf{W} \breve{\boldsymbol{\mu}}+\boldsymbol{b}$。同时定义 卡尔曼增益矩阵（Kalman gain matrix）:

\[\mathbf{K}=\mathbf{C S}^{-1} \tag{2.122}\]

由此，我们得到后验分布中的统计量

\[\begin{align} & \widehat{\boldsymbol{\mu}}=\breve{\boldsymbol{\mu}}+\mathbf{K}(\boldsymbol{y}-\boldsymbol{m}) \tag{2.123}\\ & \widehat{\boldsymbol{\Sigma}}=\breve{\boldsymbol{\Sigma}}-\mathbf{K C}^{\top} \tag{2.124} \end{align}\]

请注意

\[\mathbf{K S K}^{\top}=\mathbf{C S}^{-1} \mathbf{S S}^{-\top} \mathbf{C}^{\top}=\mathbf{C S}^{-1} \mathbf{C}^{\top}=\mathbf{K C}^{\top} \tag{2.125}\]

因此，我们也可以将后验协方差写为

\[\widehat{\boldsymbol{\Sigma}}=\breve{\boldsymbol{\Sigma}}-\mathbf{K S K}^{\top} \tag{2.126}\]

使用方程（2.93）中的矩阵求逆引理，我们还可以将后验重写为以下形式[Bis06][^Bis06]，[p93][^p93]，这需要 $O\left(L^3\right)$ 的时间复杂度而不是 $O\left(D^3\right)$ ：

\[\begin{align} & \hat{\boldsymbol{\Sigma}}=\left(\breve{\boldsymbol{\Sigma}}^{-1}+\mathbf{W}^{\boldsymbol{\top}} \boldsymbol{\Omega}^{-1} \mathbf{W}\right)^{-1} \tag{2.127}\\ & \widehat{\boldsymbol{\mu}}=\widehat{\boldsymbol{\Sigma}}\left[\mathbf{W}^{\top} \boldsymbol{\Omega}^{-1}(\boldsymbol{y}-\boldsymbol{b})+\breve{\boldsymbol{\Sigma}}^{-1} \breve{\boldsymbol{\mu}}\right] \tag{2.128} \end{align}\]

最后，请注意，后验分布对应的归一化常数只是在观测值处评估的关于 $\boldsymbol{y}$ 的边际分布：

\[\begin{align} p(\boldsymbol{y}) & =\int \mathcal{N}(\boldsymbol{z} \mid \breve{\boldsymbol{\mu}}, \breve{\boldsymbol{\Sigma}}) \mathcal{N}(\boldsymbol{y} \mid \mathbf{W} \boldsymbol{z}+\boldsymbol{b}, \boldsymbol{\Omega}) d \boldsymbol{z} \tag{2.129} \\ & =\mathcal{N}\left(\boldsymbol{y} \mid \mathbf{W} \breve{\boldsymbol{\mu}}+\boldsymbol{b}, \boldsymbol{\Omega}+\mathbf{W} \breve{\boldsymbol{\Sigma}} \mathbf{W}^{\boldsymbol{\top}}\right)=\mathcal{N}(\boldsymbol{y} \mid \boldsymbol{m}, \mathbf{S}) \tag{2.129} \end{align}\]

由此，我们可以很容易地计算出对数边际似然。我们在算法8.1中总结了所有这些方程。

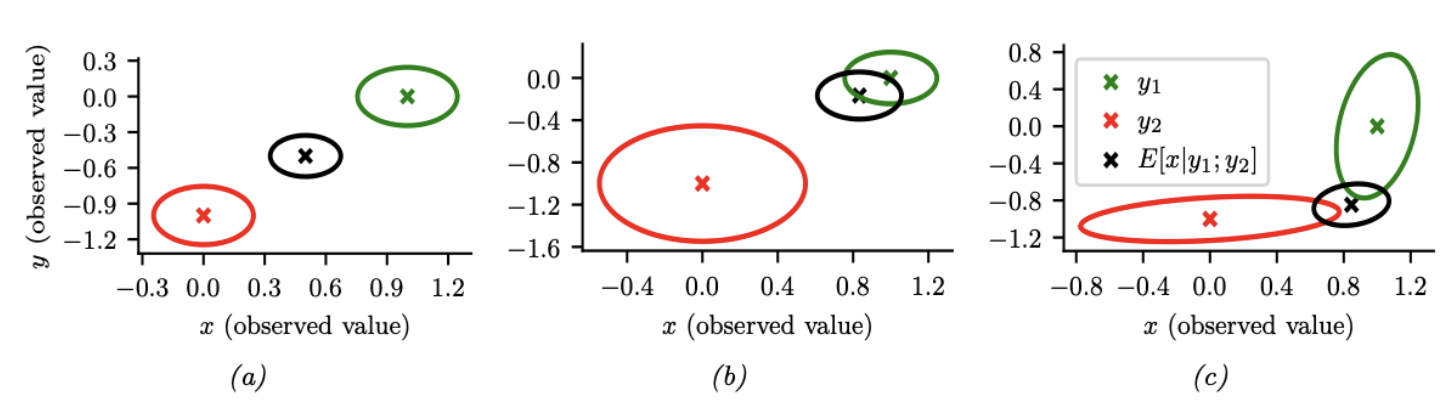
图 $2.10$：我们观察到 $\boldsymbol{x}=(0,-1)$（红叉）和 $\boldsymbol{y}=(1,0)$（绿叉），并估计 $\mathbb{E}[\boldsymbol{z} \mid \boldsymbol{x}, \boldsymbol{y}, \boldsymbol{\theta}]$（黑叉）。（a）同样可靠的传感器，因此后验均值估计位于两个圆圈之间。（b）传感器2更可靠，因此估计值更倾向于绿色圆圈。（c）传感器1在垂直方向更可靠，传感器2在水平方向更可靠。该估计值是两种测量值的适当组合。

2.3.2.3 案例：已知测量噪声进行信号融合

假设我们有一个未知的感兴趣的随机变量，$\boldsymbol{z} \sim \mathcal{N}\left(\boldsymbol{\mu}_z, \boldsymbol{\Sigma}_z\right)$，关于这个未知量，我们有两个含噪声的测量值，$\boldsymbol{x} \sim \mathcal{N}\left(\boldsymbol{z}, \boldsymbol{\Sigma}_x\right)$ 和 $\boldsymbol{y} \sim \mathcal{N}\left(\boldsymbol{z}, \boldsymbol{\Sigma}_y\right)$。从图模型角度上讲，我们可以将这个案例表示为 $\boldsymbol{x} \leftarrow \boldsymbol{z} \rightarrow \boldsymbol{y}$。这是一个线性高斯系统的例子。我们的目标是将证据结合在一起，计算 $p(\boldsymbol{z} \mid \boldsymbol{x}, \boldsymbol{y} ; \boldsymbol{\theta})$。这被称为传感器融合（sensor fusion）。（在本节中，我们假设 $\boldsymbol{\theta}=\left(\boldsymbol{\Sigma}_x, \boldsymbol{\Sigma}_y\right)$ 是已知的，更一般的情况见补充材料的第2.1.2节。）

我们可以将 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 组合成一个向量 $\boldsymbol{v}$，因此模型可以表示为 $\boldsymbol{z} \rightarrow \boldsymbol{v}$，其中 $p(\boldsymbol{v} \mid \boldsymbol{z})=\mathcal{N}\left(\boldsymbol{v} \mid \mathbf{W} \boldsymbol{z}, \boldsymbol{\Sigma}_v\right)$，其中 $\mathbf{W}=[\mathbf{I} ; \mathbf{I}]$ 和 $\boldsymbol{\Sigma}_v=\left[\boldsymbol{\Sigma}_x, \mathbf{0} ; \mathbf{0}, \boldsymbol{\Sigma}_y\right]$ 表示分块结构矩阵。然后，我们可以应用高斯贝叶斯规则（第2.3.2.2节）来计算 $p(\boldsymbol{z} \mid \boldsymbol{v})$。

图2.10（a）给出了一个2d示例，其中我们设置 $\boldsymbol{\Sigma}_x=\boldsymbol{\Sigma}_y=0.01 \mathbf{I}_2$，因此两个传感器的可靠性相同。在这种情况下，后验均值是两个观测值 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 之间的均值。在图2.10（b）中，我们设置 $\boldsymbol{\Sigma}_x=0.05 \mathbf{I}_2$ 和 $\boldsymbol{\Sigma}_y=0.01 \mathbf{I}_2$，因此传感器2比传感器1更可靠。在这种情况下，后验均值更接近 $\boldsymbol{y}$。在图2.10（c）中，我们设置

\[\boldsymbol{\Sigma}_x=0.01\left(\begin{array}{cc} 10 & 1 \\ 1 & 1 \end{array}\right), \quad \boldsymbol{\Sigma}_y=0.01\left(\begin{array}{cc} 1 & 1 \\ 1 & 10 \end{array}\right) \tag{2.130}\]

因此传感器1在第二分量（垂直方向）上更可靠并且传感器2在第一分量（水平方向）上也更可靠。在这种情况下，后验均值在垂直方向上更接近 $\boldsymbol{x}$，在水平方向上更靠近 $\boldsymbol{y}$。

2.3.3 线性高斯系统普通微积分

在本节中，我们讨论了在线性高斯系统中执行推理的一般方法。关键在于使用information形式表示的势函数（potential function）定义相关变量的联合分布。然后，我们可以很容易地推导出边缘势、乘法势和除法势以及根据观测值对其进行调节的规则。一旦我们定义了这些操作，我们就可以在信念传播算法（第9.3节）或连接树算法（补充第9.2节）中使用它们来计算感兴趣的变量。我们将在下面详细介绍如何执行这些操作；我们的表述基于[Lau92]¹⁴；[Mur02]¹⁵。

2.3.3.1 Moment and canonical parameterization

我们可以用矩形式或规范（信息）形式表示高斯分布

\[\phi(\boldsymbol{x} ; p, \boldsymbol{\mu}, \boldsymbol{\Sigma})=p \times \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \mathbf{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right) \tag{2.131}\]

其中 $p=(2 \pi)^{-n / 2}\lvert\mathbf{\Sigma}\rvert^{-\frac{1}{2}}$是保证 $\int_x \phi(\boldsymbol{x} ; p, \boldsymbol{\mu}, \mathbf{\Sigma})=1$ 的归一化常数（$n$是$\boldsymbol{x}$的维数。）。展开二次项并合并相关项，我们得到规范形式：

\[\phi(\boldsymbol{x} ; g, \boldsymbol{h}, \mathbf{K})=\exp \left(g+\boldsymbol{x}^{\boldsymbol{\top}} \boldsymbol{h}-\frac{1}{2} \boldsymbol{x}^{\boldsymbol{\top}} \mathbf{K} \boldsymbol{x}\right)=\exp \left(g+\sum_i h_i x_i-\frac{1}{2} \sum_i \sum_k K_{\mathrm{i} j} x_i x_j\right) \tag{2.132}\]

其中

\[\begin{align} \mathbf{K} & =\boldsymbol{\Sigma}^{-1} \tag{2.133}\\ \boldsymbol{h} & =\mathbf{\Sigma}^{-1} \boldsymbol{\mu} \tag{2.134}\\ g & =\log p-\frac{1}{2} \boldsymbol{\mu}^{\top} \mathbf{K} \boldsymbol{\mu} \tag{2.135} \end{align}\]

$\mathbf{K}$ 通常被称为精度矩阵。

请注意，势函数不一定是概率分布，也不一定是可归一化的（积分为1）。我们保留常数项（$p$或$g$），以便计算具体的概率值。

2.3.3.2 乘法和除法

使用规范形式的参数化，我们可以定义高斯分布的乘法和除法操作。为了将 $\phi_1\left(x_1, \ldots, x_k ; g_1, \boldsymbol{h}_1, \mathbf{K}_1\right)$ 乘以 $\phi_2\left(x_{k+1}, \ldots, x_n ; g_2, \boldsymbol{h}_2, \mathbf{K}_2\right)$，我们可以通过在适当的维度上补零，将它们都扩展到相同的域 $x_1, \ldots, x_n$ ，然后计算

\[\left(g_1, \boldsymbol{h}_1, \mathbf{K}_1\right) *\left(g_2, \boldsymbol{h}_2, \mathbf{K}_2\right)=\left(g_1+g_2, \boldsymbol{h}_1+\boldsymbol{h}_2, \mathbf{K}_1+\mathbf{K}_2\right) \tag{2.136}\]

除法定义如下:

\[\left(g_1, \boldsymbol{h}_1, \mathbf{K}_1\right) /\left(g_2, \boldsymbol{h}_2, \mathbf{K}_2\right)=\left(g_1-g_2, \boldsymbol{h}_1-\boldsymbol{h}_2, \mathbf{K}_1-\mathbf{K}_2\right) \tag{2.137}\]

2.3.3.3 边际分布

设 $\phi_W$ 是一组变量 $W$ 的势。我们可以通过边缘化来计算子集 $V \subset W$ 的势，记为$\phi_V=\sum_{W \backslash V} \phi_W$。令

\[\boldsymbol{x}=\binom{\boldsymbol{x}_1}{\boldsymbol{x}_2}, \quad \boldsymbol{h}=\binom{\boldsymbol{h}_1}{\boldsymbol{h}_2}, \quad \mathbf{K}=\left(\begin{array}{ll} \mathbf{K}_{11} & \mathbf{K}_{12} \\ \mathbf{K}_{21} & \mathbf{K}_{22} \end{array}\right), \tag{2.138}\]

其中$\boldsymbol{x}_1$具有维度$n_1$，$\boldsymbol{x}_2$具有维度$n_2$。可以证明

\[\int_{\boldsymbol{x}_1} \phi\left(\boldsymbol{x}_1, \boldsymbol{x}_2 ; g, \boldsymbol{h}, \mathbf{K}\right)=\phi\left(\boldsymbol{x}_2 ; \hat{g}, \hat{\boldsymbol{h}}, \hat{\mathbf{K}}\right) \tag{2.139}\]

其中

\[\begin{align} \hat{g} & =g+\frac{1}{2}\left(n_1 \log (2 \pi)-\log \left|\mathbf{K}_{11}\right|+\boldsymbol{h}_1^{\top} \mathbf{K}_{11}^{-1} \boldsymbol{h}_1\right) \tag{2.140}\\ \hat{\boldsymbol{h}} & =\boldsymbol{h}_2-\mathbf{K}_{21} \mathbf{K}_{11}^{-1} \boldsymbol{h}_1 \tag{2.141}\\ \hat{\mathbf{K}} & =\mathbf{K}_{22}-\mathbf{K}_{21} \mathbf{K}_{11}^{-1} \mathbf{K}_{12} \tag{2.142} \end{align}\]

2.3.3.4 以证据为条件

考虑在 $(\boldsymbol{x}, \boldsymbol{y})$ 上定义的势。假设我们观察到值 $\boldsymbol{y}$。新的势由以下降维对象给出：

\[\begin{align} & \phi^*(\boldsymbol{x})=\exp \left[g+\left(\begin{array}{ll} \boldsymbol{x}^T & \boldsymbol{y}^T \end{array}\right)\binom{\boldsymbol{h}_X}{\boldsymbol{h}_Y}-\frac{1}{2}\left(\begin{array}{ll} \boldsymbol{x}^T & \boldsymbol{y}^T \end{array}\right)\left(\begin{array}{ll} \mathbf{K}_{X X} & \mathbf{K}_{X Y} \tag{2.143}\\ \mathbf{K}_{Y X} & \mathbf{K}_{Y Y} \end{array}\right)\binom{\boldsymbol{x}}{\boldsymbol{y}}\right] \\ & =\exp \left[\left(g+\boldsymbol{h}_Y^T \boldsymbol{y}-\frac{1}{2} \boldsymbol{y}^T \mathbf{K}_{Y Y} \boldsymbol{y}\right)+\boldsymbol{x}^T\left(\boldsymbol{h}_X-\mathbf{K}_{X Y} \boldsymbol{y}\right)-\frac{1}{2} \boldsymbol{x}^T \mathbf{K}_{X X} \boldsymbol{x}\right] \tag{2.144} \end{align}\]

这将[Lau92]¹⁴中的相应方程推广到向量值的情况。

2.3.3.5 将线性高斯CPD转换为规范势

最后，我们讨论如何创建初始势，假设我们从有向高斯图形模型开始。特别是，考虑一个具有线性高斯条件概率分布（CPD）的节点：

\[\begin{align} p(\boldsymbol{x} \mid \boldsymbol{u}) & =c \exp \left[-\frac{1}{2}\left(\left(\boldsymbol{x}-\boldsymbol{\mu}-\mathbf{B}^T \boldsymbol{u}\right)^T \boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}-\mathbf{B}^T \boldsymbol{u}\right)\right)\right] \tag{2.145}\\ & =\exp \left[\begin{array}{ll} -\frac{1}{2}\left(\begin{array}{ll} \boldsymbol{x} & \boldsymbol{u} \end{array}\right)\left(\begin{array}{cc} \boldsymbol{\Sigma}^{-1} & -\boldsymbol{\Sigma}^{-1} \mathbf{B}^T \\ -\mathbf{B} \boldsymbol{\Sigma}^{-1} & \mathbf{B} \boldsymbol{\Sigma}^{-1} \mathbf{B}^T \end{array}\right)\binom{\boldsymbol{x}}{\boldsymbol{u}} \\ & +\left(\begin{array}{ll} \boldsymbol{x} & \boldsymbol{u} \end{array}\right)\binom{\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}}{-\mathbf{B} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}}-\frac{1}{2} \boldsymbol{\mu}^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}+\log c \end{array}\right] \tag{2.146-2.147} \end{align}\]

其中 $c=(2 \pi)^{-n / 2}\lvert\boldsymbol{\Sigma}\rvert^{-\frac{1}{2}}$。因此，我们将规范参数设置为

\[\begin{align} g & =-\frac{1}{2} \boldsymbol{\mu}^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}-\frac{n}{2} \log (2 \pi)-\frac{1}{2} \log |\boldsymbol{\Sigma}| \tag{2.148}\\ \boldsymbol{h} & =\binom{\boldsymbol{\Sigma} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}}{-\mathbf{B} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}} \tag{2.149}\\ \mathbf{K} & =\left(\begin{array}{cc} \boldsymbol{\Sigma} \boldsymbol{\Sigma}^{-1} & -\boldsymbol{\Sigma}^{-1} \mathbf{B}^T \\ -\mathbf{B} \boldsymbol{\Sigma}^{-1} & \mathbf{B} \boldsymbol{\Sigma}^{-1} \mathbf{B}^T \end{array}\right)=\binom{\mathbf{I}}{-\mathbf{B}} \boldsymbol{\Sigma}^{-1}\left(\begin{array}{ll} \mathbf{I} & -\mathbf{B} \end{array}\right) \tag{2.150} \end{align}\]

在 $x$ 是标量的特殊情况下，相应的结果可以在[Lau92]中找到。特别地，我们有 $\Sigma^{-1}=1 / \sigma^2$，$B=b$，以及 $n=1$，所以上式变成

\[\begin{align} g & =\frac{-\mu^2}{2 \sigma^2}-\frac{1}{2} \log \left(2 \pi \sigma^2\right) \tag{2.151}\\ \boldsymbol{h} & =\frac{\mu}{\sigma^2}\binom{1}{-\boldsymbol{b}} \tag{2.152}\\ \mathbf{K} & =\frac{1}{\sigma}\left(\begin{array}{cc} 1 & -\boldsymbol{b}^T \\ -\boldsymbol{b} & \boldsymbol{b} \boldsymbol{b}^T \end{array}\right) \tag{2.153} \end{align}\]

2.3.3.6 示例：高斯积

作为上述结果的应用，我们可以推导出两个高斯分布的（非归一化）乘积，如下所示（另见[Kaa12][^Kaa12]，第8.1.8节）：

\[\mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1\right) \times \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2\right) \propto \mathcal{N}\left(\boldsymbol{x} \mid \boldsymbol{\mu}_3, \boldsymbol{\Sigma}_3\right) \tag{2.154}\]

其中

\[\begin{align} & \boldsymbol{\Sigma}_3=\left(\boldsymbol{\Sigma}_1^{-1}+\boldsymbol{\Sigma}_2^{-1}\right)^{-1} \tag{2.155}\\ & \boldsymbol{\mu}_3=\boldsymbol{\Sigma}_3\left(\boldsymbol{\Sigma}_1^{-1} \boldsymbol{\mu}_1+\boldsymbol{\Sigma}_2^{-1} \boldsymbol{\mu}_2\right) \tag{2.156} \end{align}\]

我们看到新的高斯分布的精度是单个精度的总和，均值是单个均值的精度加权组合。我们还可以按以下方式重写结果，这只需要一次矩阵求逆：

\[\begin{align} & \boldsymbol{\Sigma}_3=\boldsymbol{\Sigma}_1\left(\boldsymbol{\Sigma}_1+\boldsymbol{\Sigma}_2\right)^{-1} \boldsymbol{\Sigma}_2 \tag{2.157}\\ & \boldsymbol{\mu}_3=\boldsymbol{\Sigma}_2\left(\boldsymbol{\Sigma}_1+\boldsymbol{\Sigma}_2\right)^{-1} \boldsymbol{\mu}_1+\boldsymbol{\Sigma}_1\left(\boldsymbol{\Sigma}_1+\boldsymbol{\Sigma}_2\right)^{-1} \boldsymbol{\mu}_2 \tag{2.158} \end{align}\]

在标量情况下，这变成

\[\mathcal{N}\left(x \mid \mu_1, \sigma_1^2\right) \mathcal{N}\left(x \mid \mu_2, \sigma_2^2\right) \propto \mathcal{N}\left(x \left\lvert\, \frac{\mu_1 \sigma_2^2+\mu_2 \sigma_1^2}{\sigma_1^2+\sigma_2^2}\right., \frac{\sigma_1^2 \sigma_2^2}{\sigma_1^2+\sigma_2^2}\right) \tag{2.159}\]

2.4 指数族分布

在本节中，我们定义了指数族（exponential family），其中覆盖许多常见的概率分布。指数族在统计学和机器学习中起着至关重要的作用，原因有很多，包括以下几点：

如第2.4.7节所述，指数族是唯一一类在给定一些用户选择的约束条件下，具有最大熵（因此做出最少假设）的分布族。
如第15.1节所述，指数族是GLM的核心。
如第10章所述，指数族是变分推理的核心。
如第2.4.5节所述，在某些正则条件下，指数族是唯一具有有限大小充分统计量的分布族。
如第3.4节所述，指数族的所有成员都有一个共轭先验[DY79]¹⁶，这简化了参数的贝叶斯推理。

2.4.1 定义

考虑一个由参数 $\boldsymbol{\eta} \in \mathbb{R}^K$ 表示的概率分布族，其定义域固定在 $\mathcal{X}^D \subseteq \mathbb{R}^D$ 上。如果分布 $p(\boldsymbol{x} \mid \boldsymbol{\eta})$ 的密度函数可以写成以下形式，我们称其属于指数族（exponential family）：

\[p(\boldsymbol{x} \mid \boldsymbol{\eta}) \triangleq \frac{1}{Z(\boldsymbol{\eta})} h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})\right]=h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-A(\boldsymbol{\eta})\right] \tag{2.160}\]

其中 $h(\boldsymbol{x})$ 表示缩放常数（又被称为base measure，通常取值为1），$\mathcal{T}(\boldsymbol{x}) \in \mathbb{R}^K$ 表示 充分统计量（sufficient statistics），$\boldsymbol{\eta}$ 为 自然参数（natural parameters）或 规范参数（canonical parameters），$Z(\boldsymbol{\eta})$ 是归一化常数，又被称为 配分函数（partition function）。$A(\boldsymbol{\eta})=\log Z(\boldsymbol{\eta})$ 表示 对数配分函数（log partition function）。在2.4.3节，我们将展示 $A$ 是一个定义在凸集合 $\Omega \triangleq\left\{\boldsymbol{\eta} \in \mathbb{R}^K: A(\boldsymbol{\eta})<\infty\right\}$ 上的凸函数。

如果自然参数彼此独立，则很方便。从形式上讲，如果不存在 $\boldsymbol{\eta} \in \mathbb{R}^K \backslash{0}$ 使得 $\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})=0$，则指数族是最小的（minimal）。在多项式分布的情况下，由于参数和为一的约束，可能会违反最后一个条件；然而，使用 $K-1$ 独立参数很容易对分布进行重新参数化，如下所示。

方程（2.160）可以通过定义 $\boldsymbol{\eta}=f(\boldsymbol{\phi})$ 来实现进一步的推广，其中 $\boldsymbol{\phi}$ 是另一组规模可能更小的参数。在这种情况下，分布具有以下形式

\[p(\boldsymbol{x} \mid \boldsymbol{\phi})=h(\boldsymbol{x}) \exp \left[f(\boldsymbol{\phi})^{\top} \mathcal{T}(\boldsymbol{x})-A(f(\boldsymbol{\phi}))\right] \tag{2.161}\]

如果从 $\boldsymbol{\phi}$ 到 $\boldsymbol{\eta}$ 的映射是非线性的，我们称对应的分布族为 曲线指数族（curved exponential family）。如果 $\boldsymbol{\eta}=f(\boldsymbol{\phi})=\boldsymbol{\phi}$，模型被称为具备 规范形式（canonical form）。如果同时满足 $\mathcal{T}(\boldsymbol{x})=\boldsymbol{x}$，我们称之为一个 自然指数族（natural exponential family，NEF）。在这种情况下，上式可以写成

\[p(\boldsymbol{x} \mid \boldsymbol{\eta})=h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \boldsymbol{x}-A(\boldsymbol{\eta})\right] \tag{2.162}\]

我们定义 矩参数（moment parameters）为充分统计向量的均值：

\[\boldsymbol{m}=\mathbb{E}[\mathcal{T}(\boldsymbol{x})] \tag{2.163}\]

接下来我们将介绍一些具体的案例。

2.4.2 案例

本节，我们将讨论一些常见的指数族分布。每一个分布对应不同的$h(\boldsymbol{x})$ 和 $\mathcal{T}(\boldsymbol{x})$ 。

2.4.2.1 伯努利分布

伯努利分布可以写成如下的指数族形式：

\[\begin{align} \operatorname{Ber}(x \mid \mu) & =\mu^x(1-\mu)^{1-x} \tag{2.164}\\ & =\exp [x \log (\mu)+(1-x) \log (1-\mu)] \tag{2.165}\\ & =\exp \left[\mathcal{T}(\boldsymbol{x})^{\top} \boldsymbol{\eta}\right] \tag{2.166} \end{align}\]

其中 $\mathcal{T}(x)=[\mathbb{I}(x=1), \mathbb{I}(x=0)], \boldsymbol{\eta}=[\log (\mu), \log (1-\mu)]$, $\mu$ 表示期望。然而，这是一种过完备（over-complete representation）的表示，因为特征之间存在线性依赖关系：

\[\mathbf{1}^{\top} \mathcal{T}(x)=\mathbb{I}(x=0)+\mathbb{I}(x=1)=1 \tag{2.167}\]

如果表征是过完备的，$\boldsymbol{\eta}$ 则无法唯一被识别。通常使用最小表示法，这意味着与分布相关的 $\boldsymbol{\eta}$ 是唯一的。在这种情况下，我们可以定义

\[\operatorname{Ber}(x \mid \mu)=\exp \left[x \log \left(\frac{\mu}{1-\mu}\right)+\log (1-\mu)\right] \tag{2.168}\]

我们可以将其转化为如下的指数族形式

\[\begin{align} \eta & =\log \left(\frac{\mu}{1-\mu}\right) \tag{2.169}\\ \mathcal{T}(x) & =x \tag{2.170} \\ A(\eta) & =-\log (1-\mu)=\log \left(1+e^\eta\right) \tag{2.171}\\ h(x) & =1 \tag{2.172} \end{align}\]

我们可以使用以下公式从规范参数 $\eta$ 中恢复均值参数 $\mu$：

\[\mu=\sigma(\eta)=\frac{1}{1+e^{-\eta}} \tag{2.173}\]

上式其实就是logistic（sigmoid）函数。

2.4.2.2 Categorical distribution

对于包含 $K$ 个类别的离散分布，我们有（其中 $x_k=\mathbb{I}(x=k)$）：

\[\begin{align} \operatorname{Cat}(x \mid \boldsymbol{\mu}) & =\prod_{k=1}^K \mu_k^{x_k}=\exp \left[\sum_{k=1}^K x_k \log \mu_k\right] \\ & =\exp \left[\sum_{k=1}^{K-1} x_k \log \mu_k+\left(1-\sum_{k=1}^{K-1} x_k\right) \log \left(1-\sum_{k=1}^{K-1} \mu_k\right)\right] \\ & =\exp \left[\sum_{k=1}^{K-1} x_k \log \left(\frac{\mu_k}{1-\sum_{j=1}^{K-1} \mu_j}\right)+\log \left(1-\sum_{k=1}^{K-1} \mu_k\right)\right] \\ & =\exp \left[\sum_{k=1}^{K-1} x_k \log \left(\frac{\mu_k}{\mu_K}\right)+\log \mu_K\right] \end{align}\]

其中 $\mu_K=1-\sum_{k=1}^{K-1} \mu_k$。上式也可以写成指数族的形式：

\[\begin{align} \operatorname{Cat}(x \mid \boldsymbol{\eta}) & =\exp \left(\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-A(\boldsymbol{\eta})\right) \\ \boldsymbol{\eta} & =\left[\log \frac{\mu_1}{\mu_K}, \ldots, \log \frac{\mu_{K-1}}{\mu_K}\right] \\ A(\boldsymbol{\eta}) & =-\log \left(\mu_K\right) \\ \mathcal{T}(x) & =[\mathbb{I}(x=1), \ldots, \mathbb{I}(x=K-1)] \\ h(x) & =1 \end{align}\]

我们可以使用以下公式从规范参数中恢复均值参数

\[\mu_k=\frac{e^{\eta_k}}{1+\sum_{j=1}^{K-1} e^{\eta_j}} \tag{2.183}\]

如果我们定义 $\eta_K=0$，上式可以写成：

\[\mu_k=\frac{e^{\eta_k}}{\sum_{j=1}^K e^{\eta_j}} \tag{2.184}\]

其中 $k=1: K$。所以 $\boldsymbol{\mu}=\operatorname{softmax}(\boldsymbol{\eta})$，其中 softmax 是公式 (15.136)中的 softmax 或 multinomial logit 函数。基于此，我们发现

\[\mu_K=1-\frac{\sum_{k=1}^{K-1} e^{\eta_k}}{1+\sum_{k=1}^{K-1} e^{\eta_k}}=\frac{1}{1+\sum_{k=1}^{K-1} e^{\eta_k}} \tag{2.185}\]

所以

\[A(\eta)=-\log \left(\mu_K\right)=\log \left(\sum_{k=1}^K e^{\eta_k}\right) \tag{2.186}\]

2.4.2.3 单变量高斯分布

单变量高斯通常可以写成：

\[\begin{align} \mathcal{N}\left(x \mid \mu, \sigma^2\right) & =\frac{1}{\left(2 \pi \sigma^2\right)^{\frac{1}{2}}} \exp \left[-\frac{1}{2 \sigma^2}(x-\mu)^2\right] \tag{2.187}\\ & =\frac{1}{(2 \pi)^{\frac{1}{2}}} \exp \left[\frac{\mu}{\sigma^2} x-\frac{1}{2 \sigma^2} x^2-\frac{1}{2 \sigma^2} \mu^2-\log \sigma\right] \tag{2.188} \end{align}\]

为了写成指数族的形式，我们定义

\[\begin{align} \eta & =\binom{\mu / \sigma^2}{-\frac{1}{2 \sigma^2}} \tag{2.189}\\ \mathcal{T}(x) & =\binom{x}{x^2} \tag{2.190}\\ A(\eta) & =\frac{\mu^2}{2 \sigma^2}+\log \sigma=\frac{-\eta_1^2}{4 \eta_2}-\frac{1}{2} \log \left(-2 \eta_2\right) \tag{2.191}\\ h(x) & =\frac{1}{\sqrt{2 \pi}} \tag{2.192} \end{align}\]

矩参数为

\[\boldsymbol{m}=\left[\mu, \mu^2+\sigma^2\right] \tag{2.193}\]

2.4.2.4 固定方差的单变量高斯

如果我们固定 $\sigma^2=1$，我们可以将高斯分布写成一个自然指数族，此时

\[\begin{align} \eta & =\mu \tag{2.194}\\ \mathcal{T}(x) & =x \tag{2.195}\\ A(\mu) & =\frac{\mu^2}{2 \sigma^2}+\log \sigma=\frac{\mu^2}{2} \tag{2.196}\\ h(x) & =\frac{1}{\sqrt{2 \pi}} \exp \left[-\frac{x^2}{2}\right]=\mathcal{N}(x \mid 0,1) \tag{2.197} \end{align}\]

此时的 $h(x)$ 不再是常数。

2.4.2.5 多变量高斯

多变量高斯分布的参数通常包括期望向量 $\boldsymbol{\mu}$ 和协方差矩阵$\boldsymbol{\Sigma}$。对应的概率密度函数为

\[\begin{align} \mathcal{N}(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma}) & =\frac{1}{(2 \pi)^{D / 2} \sqrt{\operatorname{det}(\boldsymbol{\Sigma})}} \exp \left(-\frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{x}+\boldsymbol{x}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}-\frac{1}{2} \boldsymbol{\mu}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}\right) \tag{2.198}\\ & =c \exp \left(\boldsymbol{x}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}-\frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{x}\right) \tag{2.199} \\ c & \triangleq \frac{\exp \left(-\frac{1}{2} \boldsymbol{\mu}^{\top} \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}\right)}{(2 \pi)^{D / 2} \sqrt{\operatorname{det}(\boldsymbol{\Sigma})}} \tag{2.200} \end{align}\]

然而，我们也可以使用 canonical parameters 或者 natural parameters，又被称为 information form：

\[\begin{align} \boldsymbol{\Lambda} & =\boldsymbol{\Sigma}^{-1} \tag{2.201}\\ \boldsymbol{\xi} & =\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu} \tag{2.202}\\ \mathcal{N}_c(\boldsymbol{x} \mid \boldsymbol{\xi}, \boldsymbol{\Lambda}) & \triangleq c^{\prime} \exp \left(\boldsymbol{x}^{\top} \boldsymbol{\xi}-\frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{\Lambda} \boldsymbol{x}\right) \tag{2.203}\\ c^{\prime} & =\frac{\exp \left(-\frac{1}{2} \boldsymbol{\xi}^{\top} \boldsymbol{\Lambda}^{-1} \boldsymbol{\xi}\right)}{(2 \pi)^{D / 2} \sqrt{\operatorname{det}\left(\boldsymbol{\Lambda}^{-1}\right)}} \tag{2.204} \end{align}\]

其中我们用符号 $\mathcal{N}_c()$ 来区分标准的参数化 $\mathcal{N}()$。此处 $\boldsymbol{\Lambda}$ 被称为 精度矩阵，$\boldsymbol{\xi}$ 被称为精度加权均值向量。

我们可以顺势定义指数族的表达式：

\[\begin{align} \mathcal{N}_c(\boldsymbol{x} \mid \boldsymbol{\xi}, \boldsymbol{\Lambda}) & =\underbrace{(2 \pi)^{-D / 2}}_{h(\boldsymbol{x})} \underbrace{\exp \left[\frac{1}{2} \log |\boldsymbol{\Lambda}|-\frac{1}{2} \boldsymbol{\xi}^{\top} \boldsymbol{\Lambda}^{-1} \boldsymbol{\xi}\right]}_{g(\boldsymbol{\eta})} \exp \left[-\frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{\Lambda} \boldsymbol{x}+\boldsymbol{x}^{\top} \boldsymbol{\xi}\right] \tag{2.205}\\ & =h(\boldsymbol{x}) g(\boldsymbol{\eta}) \exp \left[-\frac{1}{2} \boldsymbol{x}^{\top} \boldsymbol{\Lambda} \boldsymbol{x}+\boldsymbol{x}^{\top} \boldsymbol{\xi}\right] \tag{2.206}\\ & =h(\boldsymbol{x}) g(\boldsymbol{\eta}) \exp \left[-\frac{1}{2}\left(\sum_{i j} x_i x_j \Lambda_{i j}\right)+\boldsymbol{x}^{\top} \boldsymbol{\xi}\right] \tag{2.207}\\ & =h(\boldsymbol{x}) g(\boldsymbol{\eta}) \exp \left[-\frac{1}{2} \operatorname{vec}(\boldsymbol{\Lambda})^{\top} \operatorname{vec}\left(\boldsymbol{x} \boldsymbol{x}^{\top}\right)+\boldsymbol{x}^{\top} \boldsymbol{\xi}\right] \tag{2.208}\\ & =h(\boldsymbol{x}) \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-A(\boldsymbol{\eta})\right] \tag{2.209} \end{align}\]

其中

\[\begin{align} h(\boldsymbol{x}) & =(2 \pi)^{-D / 2} \tag{2.210}\\ \boldsymbol{\eta} & =\left[\boldsymbol{\xi} ;-\frac{1}{2} \operatorname{vec}(\boldsymbol{\Lambda})\right]=\left[\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu} ;-\frac{1}{2} \operatorname{vec}\left(\boldsymbol{\Sigma}^{-1}\right)\right] \tag{2.211}\\ \mathcal{T}(\boldsymbol{x}) & =\left[\boldsymbol{x} ; \operatorname{vec}\left(\boldsymbol{x} \boldsymbol{x}^{\top}\right)\right] \tag{2.212}\\ A(\boldsymbol{\eta}) & =-\log g(\boldsymbol{\eta})=-\frac{1}{2} \log |\boldsymbol{\Lambda}|+\frac{1}{2} \boldsymbol{\xi}^{\top} \boldsymbol{\Lambda}^{-1} \boldsymbol{\xi} \tag{2.213} \end{align}\]

从中，我们发现矩参数为

\[\boldsymbol{m}=\mathbb{E}[\mathcal{T}(\boldsymbol{x})]=\left[\boldsymbol{\mu} ; \boldsymbol{\mu} \boldsymbol{\mu}^{\top}+\mathbf{\Sigma}\right] \tag{2.214}\]

(考虑到 $\boldsymbol{\Lambda}$ 是一个对称矩阵，所以上述表达并不是一个最小表示。我们可以使用每个矩阵的上半部分或下半部分实现最小化定义。)

2.4.2.6 反例

并不是所有的分布都属于指数族。举个例子，学生分布不属于指数族，因为它的概率密度函数（式2.30）不满足特定的形式。（然而，指数族存在某一个推广，即 $\phi$-指数族[Nau04][^Nau04];[Tsa88][^Tsa88]，后者包含学生分布。）

考虑均匀分布这一更微妙的例子，$Y \sim \operatorname{Unif}\left(\theta_1, \theta_2\right)$。概率密度函数的定义为

\[p(y \mid \boldsymbol{\theta})=\frac{1}{\theta_2-\theta_1} \mathbb{I}\left(\theta_1 \leq y \leq \theta_2\right) \tag{2.215}\]

人们很容易认为这是指数族，$h(y)=1$，$\mathcal{T}(y)=\boldsymbol{0}$，$Z(\boldsymbol{\theta})=\theta_2-\theta_1$。然而，这种分布的支撑集（即 $\mathcal{Y}={y: p(y)>0})$ 取决于参数 $\boldsymbol{\theta}$，这违反了指数族的假设。

2.4.3 对数配分函数是累积量生成函数

一个分布的一阶和二阶 累积量（cumulants）为期望 $\mathbb{E}[X]$ 和方差 $\mathbb{V}[X]$，而一阶矩和二阶矩为 $\mathbb{E}[X]$ 和 $\mathbb{E}\left[X^2\right]$。我们也可以计算出更高阶的累积量（和矩）。指数族分布的一个重要特性是对数配分函数的导数可以用来生成充分统计量的累积值。具体而言，一阶和二阶累积量为：

\[\begin{align} & \nabla_{\boldsymbol{\eta}} A(\boldsymbol{\eta})=\mathbb{E}[\mathcal{T}(\boldsymbol{x})] \tag{2.216}\\ & \nabla_\boldsymbol{\eta}^2 A(\boldsymbol{\eta})=\operatorname{Cov}[\mathcal{T}(\boldsymbol{x})] \tag{2.217} \end{align}\]

接下来我们将给出证明。

2.4.3.1 期望的推导

为简单期间，我们仅考虑1维的情况

\[\begin{align} \frac{d A}{d \eta} & =\frac{d}{d \eta}\left(\log \int \exp (\eta \mathcal{T}(x)) h(x) d x\right) \tag{2.218}\\ & =\frac{\frac{d}{d \eta} \int \exp (\eta \mathcal{T}(x)) h(x) d x}{\int \exp (\eta \mathcal{T}(x)) h(x) d x} \tag{2.219}\\ & =\frac{\int \mathcal{T}(x) \exp (\eta \mathcal{T}(x)) h(x) d x}{\exp (A(\eta))} \tag{2.220}\\ & =\int \mathcal{T}(x) \exp (\eta \mathcal{T}(x)-A(\eta)) h(x) d x \tag{2.221}\\ & =\int \mathcal{T}(x) p(x) d x=\mathbb{E}[\mathcal{T}(x)] \tag{2.222} \end{align}\]

举例而言，考虑伯努利分布。我们有 $A(\eta)=\log \left(1+e^\eta\right)$，所以期望为

\[\frac{d A}{d \eta}=\frac{e^\eta}{1+e^\eta}=\frac{1}{1+e^{-\eta}}=\sigma(\eta)=\mu \tag{2.223}\]

2.4.3.2 方差的推导

为简单起见，我们仅考虑1维的情况。二阶导数为

\[\begin{align} \frac{d^2 A}{d \eta^2} & =\frac{d}{d \eta} \int \mathcal{T}(x) \exp (\eta \mathcal{T}(x)-A(\eta)) h(x) d x \tag{2.224}\\ & =\int \mathcal{T}(x) \exp (\eta \mathcal{T}(x)-A(\eta)) h(x)\left(\mathcal{T}(x)-A^{\prime}(\eta)\right) d x \tag{2.225}\\ & =\int \mathcal{T}(x) p(x)\left(\mathcal{T}(x)-A^{\prime}(\eta)\right) d x \tag{2.226}\\ & =\int \mathcal{T}^2(x) p(x) d x-A^{\prime}(\eta) \int \mathcal{T}(x) p(x) d x \tag{2.227}\\ & =\mathbb{E}\left[\mathcal{T}^2(X)\right]-\mathbb{E}[\mathcal{T}(x)]^2=\mathbb{V}[\mathcal{T}(x)] \tag{2.228} \end{align}\]

其中我们使用了 $A^{\prime}(\eta)=\frac{d A}{d \eta}=\mathbb{E}[\mathcal{T}(x)]$。举例而言，对于伯努利分布我们有

\[\begin{align} \frac{d^2 A}{d \eta^2} & =\frac{d}{d \eta}\left(1+e^{-\eta}\right)^{-1}=\left(1+e^{-\eta}\right)^{-2} e^{-\eta} \tag{2.229}\\ & =\frac{e^{-\eta}}{1+e^{-\eta}} \frac{1}{1+e^{-\eta}}=\frac{1}{e^\eta+1} \frac{1}{1+e^{-\eta}}=(1-\mu) \mu \tag{2.230} \end{align}\]

2.4.3.3 与Fisher信息矩阵的联系

在3.3.4 节，我们将表明，在某些正则条件下，Fisher信息矩阵定义为

\[\mathbf{F}(\eta) \triangleq \mathbb{E}_{p(\boldsymbol{x} \mid \eta)}\left[\nabla \log p(\boldsymbol{x} \mid \eta) \nabla \log p(\boldsymbol{x} \mid \eta)^{\top}\right]=-\mathbb{E}_{p(\boldsymbol{x} \mid \eta)}\left[\nabla_\eta^2 \log p(\boldsymbol{x} \mid \eta)\right] \tag{2.231}\]

所以对于指数族分布我们有

\[\mathbf{F}(\eta)=-\mathbb{E}_{p(\boldsymbol{x} \mid \boldsymbol{\eta})}\left[\nabla_{\boldsymbol{\eta}}^2\left(\boldsymbol{\eta}^{\top} \mathcal{T}(\boldsymbol{x})-A(\boldsymbol{\eta})\right)\right]=\nabla_\eta^2 A(\eta)=\operatorname{Cov}[\mathcal{T}(\boldsymbol{x})] \tag{2.232}\]

所以对数配分函数的Hessian矩阵与Fisher信息矩阵相同，同时与协方差矩阵相同。参考3.3.4.6节介绍更多细节。

2.4.4 Canonical (natural) 对比 mean (moment) 参数

令 $\Omega$ 表示可归一化的自然参数的集合：

\[\Omega \triangleq\left\{\boldsymbol{\eta} \in \mathbb{R}^K: Z(\eta)<\infty\right\} \tag{2.233}\]

我们称一个指数族是 regular 的，如果 $\Omega$ 是一个开集合。可以证明 $\Omega$ 是一个凸集，$A(\eta)$ 是定义在该集上的凸函数。

在2.4.3节，我们证明了对数配分函数的一阶导数是统分统计量的期望，即

\[\boldsymbol{m}=\mathbb{E}[\mathcal{T}(\boldsymbol{x})]=\nabla_\boldsymbol{\eta} A(\boldsymbol{\eta}) \tag{2.234}\]

对于分布 $p$，有效矩参数的集合由下式给出

\[\mathcal{M}=\left\{\boldsymbol{m} \in \mathbb{R}^K: \mathbb{E}_p[\mathcal{T}(\boldsymbol{x})]=\boldsymbol{m}\right\} \tag{2.235}\]

我们已经看到，我们可以使用以下公式从自然参数转换为矩参数

\[\boldsymbol{m}=\nabla_\eta A(\boldsymbol{\eta}) \tag{2.236}\]

如果指数族是最小表达，可以证明这一点

\[\boldsymbol{\eta}=\nabla_\boldsymbol{m} A^*(\boldsymbol{m}) \tag{2.237}\]

其中 $A^*(\boldsymbol{m})$ 是 $A$ 的凸共轭：

\[A^*(\boldsymbol{m}) \triangleq \sup _{\boldsymbol{\eta} \in \Omega} \boldsymbol{\mu}^{\top} \boldsymbol{\eta}-A(\boldsymbol{\eta}) \tag{2.238}\]

因此，这对算子 $\left(\nabla A, \nabla A^*\right)$ 让我们在自然参数 $\boldsymbol{\eta} \in \Omega$ 和均值参数 $\boldsymbol{m} \in \mathcal{M}$ 之间来回切换。

为便于将来参考，请注意与 $A$ 和 $A^*$ 相关的Bregman divergences（第5.1.10节）如下：

\[\begin{align} B_A\left(\boldsymbol{\lambda}_1 \| \boldsymbol{\lambda}_2\right) & =A\left(\boldsymbol{\lambda}_1\right)-A\left(\boldsymbol{\lambda}_2\right)-\left(\boldsymbol{\lambda}_1-\boldsymbol{\lambda}_2\right)^{\top} \nabla_{\boldsymbol{\lambda}} A\left(\boldsymbol{\lambda}_2\right) \tag{2.239}\\ B_{A^*}\left(\boldsymbol{\mu}_1 \| \boldsymbol{\mu}_2\right) & =A\left(\boldsymbol{\mu}_1\right)-A\left(\boldsymbol{\mu}_2\right)-\left(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2\right)^{\top} \nabla_{\boldsymbol{\mu}} A\left(\boldsymbol{\mu}_2\right) \tag{2.240} \end{align}\]

2.4.5 指数族分布的MLE

指数族分布的似然函数具备如下的形式

\[p(\mathcal{D} \mid \boldsymbol{\eta})=\left[\prod_{n=1}^N h\left(\boldsymbol{x}_n\right)\right] \exp \left(\boldsymbol{\eta}^{\top}\left[\sum_{n=1}^N \mathcal{T}\left(\boldsymbol{x}_n\right)\right]-N A(\boldsymbol{\eta})\right) \propto \exp \left[\boldsymbol{\eta}^{\top} \mathcal{T}(\mathcal{D})-N A(\boldsymbol{\eta})\right] \tag{2.242}\]

其中 $\mathcal{T}(\mathcal{D})$ 表示充分统计量：

\[\mathcal{T}(\mathcal{D})=\left[\sum_{n=1}^N \mathcal{T}_1\left(\boldsymbol{x}_n\right), \ldots, \sum_{n=1}^N \mathcal{T}_K\left(\boldsymbol{x}_n\right)\right] \tag{2.243}\]

对于伯努利分布，我们有 $\mathcal{T}(\mathcal{D})=\left[\sum_n \mathbb{I}\left(x_n=1\right)\right]$，对于单变量高斯，我们有 $\mathcal{T}(\mathcal{D})=\left[\sum_n x_n, \sum_n x_n^2\right]$。

Pitman-Koopman-Darmois theorem 表明，在一定的正则性条件下，指数族是唯一具有有限充分统计量的分布族。（这里，有限意味着与数据集大小无关的大小。）换句话说，对于具有自然参数 $\boldsymbol{\eta}$ 的指数族，我们有

\[p(\mathcal{D} \mid \boldsymbol{\eta})=p(\mathcal{T}(\mathcal{D}) \mid \boldsymbol{\eta}) \tag{2.244}\]

我们现在展示如何使用这个结果来计算MLE。对数似然由下式给出

\[\log p(\mathcal{D} \mid \boldsymbol{\eta})=\boldsymbol{\eta}^{\top} \mathcal{T}(\mathcal{D})-N A(\boldsymbol{\eta})+\text { const } \tag{2.245}\]

由于 $-A(\boldsymbol{\eta})$ 是定义在 $\boldsymbol{\eta}$ 上的凹函数，$\boldsymbol{\eta}^{\top} \mathcal{T}(\mathcal{D})$ 是关于 $\boldsymbol{\eta}$ 的线性函数，所以对数似然是凹函数，因此有一个唯一的全局最大值。为了推导出这个最大值，我们使用以下事实（如第2.4.3节所示），即对数配分函数的导数等于充分统计向量的期望值：

\[\nabla_{\boldsymbol{\eta}} \log p(\mathcal{D} \mid \boldsymbol{\eta})=\nabla_{\boldsymbol{\eta}} \boldsymbol{\eta}^{\top} \mathcal{T}(\mathcal{D})-N \nabla_{\boldsymbol{\eta}} A(\boldsymbol{\eta})=\mathcal{T}(\mathcal{D})-N \mathbb{E}[\mathcal{T}(\boldsymbol{x})] \tag{2.246}\]

对于单个数据点，上式变成

\[\nabla_{\boldsymbol{\eta}} \log p(\boldsymbol{x} \mid \boldsymbol{\eta})=\mathcal{T}(\boldsymbol{x})-\mathbb{E}[\mathcal{T}(\boldsymbol{x})] \tag{2.247}\]

将方程（2.246）中的梯度设置为零，我们得到MLE所满足的条件，即充分统计量的经验平均值必须等于模型的理论预期充分统计量，即 $\hat{\boldsymbol{\eta}}$ 必须满足

\[\mathbb{E}[\mathcal{T}(\boldsymbol{x})]=\frac{1}{N} \sum_{n=1}^N \mathcal{T}\left(\boldsymbol{x}_n\right) \tag{2.248}\]

这被称为 矩匹配（moment matching）。举例而言，在伯努利分布中，我们有 $\mathcal{T}(x)=\mathbb{I}(X=1)$，所以 MLE 满足

\[\mathbb{E}[\mathcal{T}(x)]=p(X=1)=\mu=\frac{1}{N} \sum_{n=1}^N \mathbb{I}\left(x_n=1\right) \tag{2.249}\]

2.4.6 Exponential dispersion family

在本节中，我们考虑自然指数族的一个扩展，称为exponential dispersion family。当我们在第15.1节讨论GLM时，这将非常有用。对于标量变量，其形式如下：

\[p\left(x \mid \eta, \sigma^2\right)=h\left(x, \sigma^2\right) \exp \left[\frac{\eta x-A(\eta)}{\sigma^2}\right] \tag{2.250}\]

其中 $\sigma^2$ 被称为 dispersion parameter。对于固定的 $\sigma^2$，这被称为自然指数族。

2.4.7 指数族的最大熵推导

假设我们想找到一个分布 $p(\boldsymbol{x})$ 来描述某些数据，我们已知的全部信息是某个特征或函数 $f_k(\boldsymbol{x})$ 的期望值 $F_k$：

\[\int d \boldsymbol{x} p(\boldsymbol{x}) f_k(\boldsymbol{x})=F_k \tag{2.251}\]

比方说， $f_1$ 可能计算 $x$，$f_2$ 可能计算 $x^2$，此时 $F_1$ 是经验期望，$F_2$ 为经验二阶矩。我们对于真实分布的先验为 $q(x)$。

为了形式化我们所说的“最少假设数”的含义，我们将搜索在KL散度的意义上，尽可能接近我们先验 $q(\boldsymbol{x})$的分布，同时满足我们的约束。

如果我们使用均匀先验 $q(\boldsymbol{x}) \propto 1$，则最小化KL散度相当于最大化熵（第5.2节）。其结果被称为最大熵模型（maximum entropy model）。

为了最小化 $\text{KL}$ 的同时满足约束（2.251），$p(x) \geq 0$ 以及 $\sum_x p(x)=1$，我们需要使用拉格朗日乘子法。

\[J(p, \boldsymbol{\lambda})=-\sum_{\boldsymbol{x}} p(\boldsymbol{x}) \log \frac{p(\boldsymbol{x})}{q(\boldsymbol{x})}+\lambda_0\left(1-\sum_{\boldsymbol{x}} p(\boldsymbol{x})\right)+\sum_k \lambda_k\left(F_k-\sum_{\boldsymbol{x}} p(\boldsymbol{x}) f_k(\boldsymbol{x})\right) \tag{2.252}\]

我们可以使用变分法对函数 $p$ 求导数，但我们将采用更简单的方法，将 $p$ 视为固定长度的向量（因为我们假设 $\boldsymbol{x}$ 是离散的）。那么我们有

\[\frac{\partial J}{\partial p_c}=-1-\log \frac{p(x=c)}{q(x=c)}-\lambda_0-\sum_k \lambda_k f_k(x=c) \tag{2.253}\]

令 $\frac{\partial J}{\partial p_c}=0$ ，我们有

\[p(\boldsymbol{x})=\frac{q(\boldsymbol{x})}{Z} \exp \left(-\sum_k \lambda_k f_k(\boldsymbol{x})\right) \tag{2.254}\]

其中我们定义 $Z \triangleq e^{1+\lambda_0}$。使用和为1的约束，我们有

\[1=\sum_x p(\boldsymbol{x})=\frac{1}{Z} \sum_{\boldsymbol{x}} q(\boldsymbol{x}) \exp \left(-\sum_k \lambda_k f_k(\boldsymbol{x})\right) \tag{2.255}\]

所以归一化常数为

\[Z=\sum_{\boldsymbol{x}} q(\boldsymbol{x}) \exp \left(-\sum_k \lambda_k f_k(\boldsymbol{x})\right) \tag{2.256}\]

这正是指数族的形式，其中 $f(x)$ 是充分统计量的向量，$-\lambda$ 是自然参数，$q(\boldsymbol{x})$则是我们的基本度量。

例如，如果特征为 $f_1(x)=x$ 和 $f_2(x)=x^2$ ，并且我们想匹配一阶矩和二阶矩，我们得到高斯分布。

2.5 Transformations of random variables

假设 $\boldsymbol{x} \sim p_x(\boldsymbol{x})$ 是某个随机变量，$\boldsymbol{y}=f(\boldsymbol{x})$ 表示某个确定的变换函数。本节，我们将讨论如何计算 $p_y(\boldsymbol{y})$。

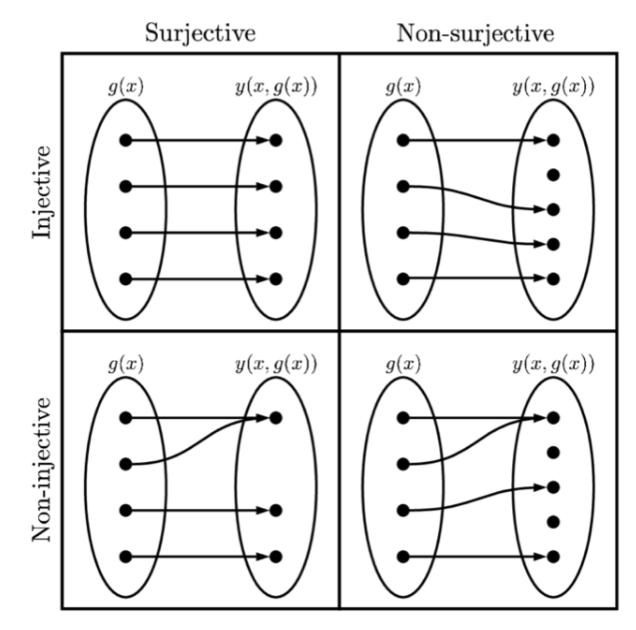
图 $2.11$：单射函数和满射函数的说明。

2.5.1 可逆变换（bijections）

如果 $f$ 是一个从 $\mathbb{R}^n$ 到 $\mathbb{R}^n$ 的 bijection。（一个双射（bijection）是一个既是单射（injective）或一对一的，又是满射（surjective）的函数，如图 2.11 所示；这意味着该函数具有明确定义的逆函数。）假设我们想计算 $\boldsymbol{y}=f(\boldsymbol{x})$ 的pdf。变量替换公式（change of variables）告诉我们

\[p_y(\boldsymbol{y})=p_x\left(f^{-1}(\boldsymbol{y})\right)\left|\operatorname{det}\left[\mathbf{J}_{f-1}(\boldsymbol{y})\right]\right| \tag{2.257}\]

其中 $\mathbf{J}_{f-1}(\boldsymbol{y})$ 表示逆变换 $f^{-1}$ 在 $\boldsymbol{y}$ 处的雅各比矩阵，$\lvert\operatorname{det} \mathbf{J}\rvert$ 表示 $\mathbf{J}$ 的行列式的绝对值。换句话说，

\[\mathbf{J}_{f^{-1}}(\boldsymbol{y})=\left(\begin{array}{ccc} \frac{\partial x_1}{\partial y_1} & \cdots & \frac{\partial x_1}{\partial y_n} \\ & \vdots & \\ \frac{\partial x_n}{\partial y_1} & \cdots & \frac{\partial x_n}{\partial y_n} \end{array}\right) \tag{2.258}\]

如果雅各比矩阵是对角矩阵，那行列式将退化为主对角线元素的乘积：

\[\operatorname{det}(\mathbf{J})=\prod_{i=1}^n \frac{\partial x_i}{\partial y_i} \tag{2.259}\]

图 $2.12$：非线性变换下密度的转换示例。注意，变换后的分布的众数并不是原始众数的变换。改编自[Bis06][^Bis06]的习题 1.4。

2.5.2 蒙特卡洛近似

有时计算雅可比行列式会很困难。在这种情况下，我们可以进行蒙特卡洛近似，通过从分布中抽取 $S$ 个样本 $\boldsymbol{x}^x \sim p(\boldsymbol{x})$ ，计算 $\boldsymbol{y}^s=f\left(\boldsymbol{x}^s\right)$，然后构建经验概率密度函数（pdf）

\[p_{\mathcal{D}}(\boldsymbol{y})=\frac{1}{S} \sum_{s=1}^S \delta\left(\boldsymbol{y}-\boldsymbol{y}^*\right)\]

举例来说，令 $x \sim \mathcal{N}(6,1)$，并且 $y=f(x)$，其中 $f(x)=\frac{1}{1+\exp (-x+5)}$。我们使用蒙特卡洛近似 $p(y)$，如图 2.12 所示。

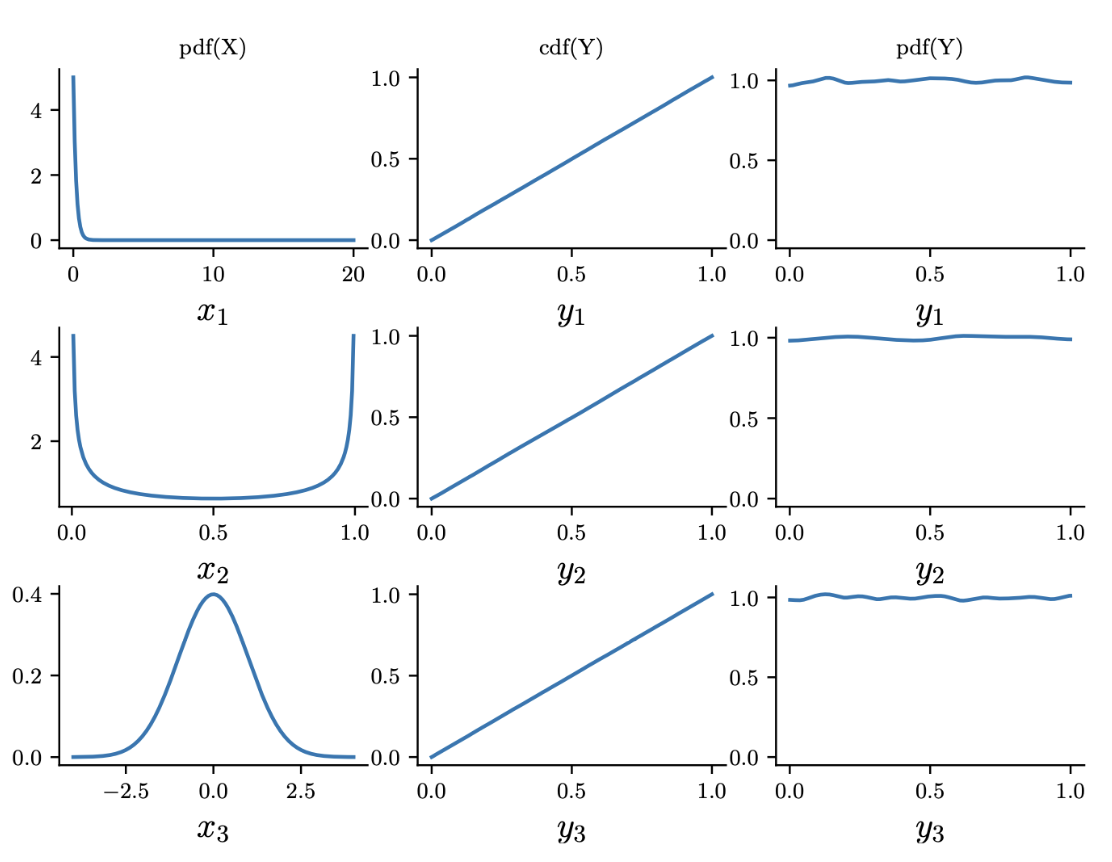
图 $2.13$：概率积分变换的插图。左列：从 3 个不同的概率密度函数 $p(X)$ 中采样的 $x_n \sim p(x)$。中列：$y_n=P_X\left(x_n\right)$ 的经验累积分布函数 (CDF)。右列：使用核密度估计法的 $p\left(y_n\right)$ 的经验概率密度函数 (PDF)。改编自 [MKL11][^MKL11] 图 11.17。

图 $2.14$：Kolmogorov-Smirnov（K-S）统计量的示意图。红线是模型的累积分布函数（cdf），蓝线是经验累积分布函数（cdf），黑色箭头表示K–S统计量。来源：https://en.wikipedia.org/wiki/Kolmogorov-Smirnov_test，经过维基百科作者Bscan的友好许可使用。

2.5.3 概率积分变换

假设 $X$ 是一个随机变量，其累积分布函数为 $P_X$。令 $Y(X)=P_X(X)$ 为 $X$ 的一个变换。我们现在证明，$Y$ 服从均匀分布，这一结果被称为概率积分变换（Probability Integral Transform, PIT）：

\[\begin{align} P_Y(y) & =\operatorname{Pr}(Y \leq y)=\operatorname{Pr}\left(P_X(X) \leq y\right) \tag{2.261}\\ & =\operatorname{Pr}\left(X \leq P_X^{-1}(y)\right)=P_X\left(P_X^{-1}(y)\right)=y \tag{2.262} \end{align}\]

比方说，在图2.13中，我们在左侧展示了不同的概率密度函数 $p_X$。我们从这些分布中采样得到 $x_n \sim p_x$。接下来通过计算 $y_n=P_X\left(x_n\right)$并排序，得到关于变量 $Y=P_X(X)$ 经验累积概率分布，结果展示在中列，表明分布是均匀分布。我们也可以通过使用核密度估计来逼近 $Y$ 的概率密度函数（pdf）；这一过程展示在右侧列中，我们可以看到它（大致上）是平坦的。

我们可以使用PIT来测试一组样本是否来自某个给定的分布，方法是使用Kolmogorov-Smirnov（K-S）检验。为此，我们绘制样本的经验累积分布函数（CDF）和分布的理论累积分布函数，并计算这两条曲线之间的最大距离，如图2.14所示。形式上，K-S统计量定义为：

\[D_n=\max _x\left|P_n(x)-P(x)\right| \tag{2.263}\]

其中，$n$ 是样本量，$P_n$ 是经验累积分布函数 (cdf)，$P$ 是理论累积分布函数 (cdf)。如果样本来自 $P$，则当 $n$ 趋于无穷大 ($n \rightarrow \infty$) 时，$D_n$ 的值应趋近于 0。

PIT 的另一个应用是从一个分布中生成样本：如果我们有从均匀分布中采样的方法，即 $u_n \sim \operatorname{Unif}(0,1)$，我们可以通过设置 $x_n=P_X^{-1}\left(u_n\right)$将其转换为来自任何其他分布的样本，其中 $P_X$ 是该分布的累积分布函数 (cdf)。

2.6 马尔可夫链

假设 $\boldsymbol{x}_t$ 包含关于这个系统的所有相关信息。这意味着它是预测未来状态的一个 充分统计量（sufficient statistic），即对于任意的 $\tau \geq 0$，我们有

\[p\left(\boldsymbol{x}_{t+\tau} \mid \boldsymbol{x}_t, \boldsymbol{x}_{1: t-1}\right)=p\left(\boldsymbol{x}_{t+\tau} \mid \boldsymbol{x}_t\right) \tag{2.264}\]

这被称为 马尔可夫假设（Markov assumption）。在这种情况下，任意长度的序列服从联合概率分布：

\[p\left(\boldsymbol{x}_{1: T}\right)=p\left(\boldsymbol{x}_1\right) p\left(\boldsymbol{x}_2 \mid \boldsymbol{x}_1\right) p\left(\boldsymbol{x}_3 \mid \boldsymbol{x}_2\right) p\left(\boldsymbol{x}_4 \mid \boldsymbol{x}_3\right) \ldots=p\left(\boldsymbol{x}_1\right) \prod_{t=2}^T p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right) \tag{2.265}\]

这被称为 马尔可夫链（Markov chain）或者 马尔可夫模型（Markov model）。接下来我们将介绍这个主题的相关基础，更多细节可参考 [Kun20]¹⁷。

2.6.1 参数化

本节，我们将讨论如何参数化马尔可夫模型。

2.6.1.1 马尔可夫转移核

条件概率分布 $p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)$ 被称为 转移函数（transition function），转移核（transition kernel）或者 马尔可夫核（Markov kernel）。该条件分布满足约束 $p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right) \geq 0$ 和 $\int_{\boldsymbol{x} \in \mathcal{X}} d x p\left(x_t=x \mid x_{t-1}\right)=1$ 。

如果我们假设转移函数 $p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{1: t-1}\right)$ 与时间无关，此时的模型被称为是 homogeneous, stationary, or time-invariant。这便是 parameter tying，因为同样的参数在不同的变量之间共享。上述假设允许我们使用固定数量的参数对任意数量的变量进行建模。在剩下的内容中，我们的讨论将基于这个假设。

图 $2.15$：一些简单的马尔可夫链的状态转移图。左：2-状态链。右：3-状态链。

2.6.1.2 马尔可夫转移矩阵

本节，我们假设变量是离散的，也就是 $X_t \in{1, \ldots, K}$。这被称为 有限状态马尔可夫链（finite-state Markov chain）。在这种情况下，条件概率分布 $p\left(X_t \mid X_{t-1}\right)$ 可以表示成一个大小为 $K \times K$ 的矩阵 $\mathbf{A}$，被称为 转移矩阵（transition matrix），其中 $A_{i j}=p\left(X_t=j \mid X_{t-1}=i\right)$ 表示从状态 $i$ 过渡到状态 $j$ 的概率。矩阵的每一行满足 $\sum_j A_{i j}=1$，所以又被称为 随机矩阵（stochastic matrix）。

stationary的有限状态马尔可夫链等价于随机自动机（stochastic automaton）。通常通过绘制有向图来可视化这种自动机，其中节点表示状态，箭头表示合法转移，对应 $\mathbf{A}$ 中的非零元素。这被称为状态转换图（state transition diagram）。与弧相关的权重表示转移概率。如图2.15(a) 所示的2-状态链：

\[\mathbf{A}=\left(\begin{array}{cc} 1-\alpha & \alpha \\ \beta & 1-\beta \end{array}\right) \tag{2.266}\]

以及图2.15(b) 所示的 3-状态链：

\[\mathbf{A}=\left(\begin{array}{ccc} A_{11} & A_{12} & 0 \\ 0 & A_{22} & A_{23} \\ 0 & 0 & 1 \end{array}\right) \tag{2.267}\]

上式又被称为 left-to-right transition matrix。

转移矩阵的元素 $A_{ij}$ 指定了在单步转移过程中从状态 $i$ 到状态 $j$ 的概率， $n$ 步的转移矩阵 $\mathbf{A}(n)$ 定义为

\[A_{i j}(n) \triangleq p\left(X_{t+n}=j \mid X_t=i\right) \tag{2.268}\]

表示 $n$ 步转移后从状态 $i$ 到状态 $j$ 的概率。显然 $\mathbf{A}(1)=\mathbf{A}$。Chapman-Kolmogorov方程指出：

\[A_{i j}(m+n)=\sum_{k=1}^K A_{i k}(m) A_{k j}(n) \tag{2.269}\]

换句话说，在$m+n$步中从 $i$ 到 $j$ 的概率就是在 $m$ 步中从 $i$ 到 $k$，然后在 $n$ 步中再从 $k$ 到 $j$ 的可能性，在所有 $k$ 上求和。式（2.269）的矩阵乘法形式为

\[\mathbf{A}(m+n)=\mathbf{A}(m) \mathbf{A}(n) \tag{2.270}\]

所以

\[\mathbf{A}(n)=\mathbf{A} \mathbf{A}(n-1)=\mathbf{A} \mathbf{A} \mathbf{A}(n-2)=\cdots=\mathbf{A}^n \tag{2.271}\]

因此，我们可以通过“powering up”转移矩阵来模拟马尔可夫链的多个步骤。

2.6.1.3 高阶马尔可夫模型

一阶马尔可夫的假设还是太强了。我们可以将一阶模型推广到高阶版本，此时当前状态依赖最近的 $n$ 个观测值，对应的联合概率分布为：

\[p\left(\boldsymbol{x}_{1: T}\right)=p\left(\boldsymbol{x}_{1: n}\right) \prod_{t=n+1}^T p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-n: t-1}\right) \tag{2.272}\]

这被称为 n 阶马尔可夫模型。如果 $n=1$，上式被称为 二元模型（bigram model），因为我们需要建立成对状态之间的关系。如果 $n=2$，上式被称为 三元模型（trigram model），因为我们需要建立状态三元组之间的关系 $p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_{t-2}\right)$。总体而言，上式被称为 n-gram model。

然而，请注意，我们总是可以通过定义一个包含过去 $n$ 个观测值的增广状态空间，将高阶马尔可夫模型转换为一阶马尔可夫模型。比方说，如果 $n=2$，我们定义 $\tilde{\boldsymbol{x}}_t=\left(\boldsymbol{x}_{t-1}, \boldsymbol{x}_t\right)$ 并定义联合概率分布为：

\[p\left(\tilde{\boldsymbol{x}}_{1: T}\right)=p\left(\tilde{\boldsymbol{x}}_2\right) \prod_{t=3}^T p\left(\tilde{\boldsymbol{x}}_t \mid \tilde{\boldsymbol{x}}_{t-1}\right)=p\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right) \prod_{t=3}^T p\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_{t-2}\right)\]

所以，在接下来的讨论中我们集中在一阶模型。

图 $2.16$：基于 King James Bible 训练的10-gram 字符级马尔可夫模型的示例输出。前缀“christians”作为模型的输入。

2.6.2 应用：语言模型

马尔可夫模型的一个重要应用是创建语言模型（language models，LM），这些模型可以生成（或评价）一系列单词。当我们使用长度为 $m=n-1$ 的有限状态马尔可夫模型时，它被称为 n-gram模型。例如，如果$m=1$，我们得到一个unigram模型（不依赖于前面的单词）；如果$m=2$，我们得到一个bigram模型（取决于前一个单词）；如果$m=3$，我们得到一个trigram模型（取决于前两个词）等。一些生成的文本见图2.16。

如今，大多数LM都是使用具有无限内存的循环神经网络构建的（见第16.3.4节）。然而，当用足够的数据训练时，简单的n-gram模型仍然可以做得很好[Che17]¹⁸。

语言模型有各种应用，例如作为拼写纠正的先验（见第29.3.3节）或自动语音识别。此外，条件语言模型可用于在给定输入的情况下生成序列，例如将一种语言映射到另一种语言，或将图像映射到序列等。

2.6.3 参数估计

在本节中，我们将讨论如何估计马尔可夫模型的参数。

图 $2.17$：（a） Hinton图显示了H.G.Wells的《时间机器》一书中估计的字符二元组计数。字符按单字频率递减排序；第一个是空格字符。最常见的二元组是“e-”，其中-表示空格。（b）与（a）相同，但每一行都在列之间进行了标准化。。

2.6.3.1 极大似然估计

长度为 $T$ 的任何特定序列的概率由下式给出：

\[\begin{align} p\left(x_{1: T} \mid \boldsymbol{\theta}\right) & =\pi\left(x_1\right) A\left(x_1, x_2\right) \ldots A\left(x_{T-1}, x_T\right) \tag{2.274}\\ & =\prod_{j=1}^K\left(\pi_j\right)^{\mathrm{I}\left(x_1=j\right)} \prod_{t=2}^T \prod_{j=1}^K \prod_{k=1}^K\left(A_{j k}\right)^{\mathrm{I}\left(x_t=k, x_{t-1}=j\right)} \tag{2.275} \end{align}\]

所以 $N$ 个序列 $\mathcal{D}=\left(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_N\right)$ 的对数似然为：

\[\log p(\mathcal{D} \mid \boldsymbol{\theta})=\sum_{i=1}^N \log p\left(\boldsymbol{x}_i \mid \boldsymbol{\theta}\right)=\sum_j N_j^1 \log \pi_j+\sum_j \sum_k N_{j k} \log A_{j k} \tag{2.276}\]

其中 $\boldsymbol{x}_i=\left(x_{i 1}, \ldots, x_{i, T_i}\right)$ 表示长度为 $T_i$ 的序列。

接下来，我们定义如下的统计量：

\[N_j^1 \triangleq \sum_{i=1}^N \mathbb{I}\left(x_{i 1}=j\right), \quad N_{j k} \triangleq \sum_{i=1}^N \sum_{t=1}^{T_i-1} \mathbb{I}\left(x_{i, t}=j, x_{i, t+1}=k\right), \quad N_j=\sum_k N_{j k} \tag{2.277}\]

考虑到和为1的约束，可以证明（参见[Mur22，第4.2.4]节）参数的MLE由归一化计数给出：

\[\hat{\pi}_j=\frac{N_j^1}{\sum_{j^{\prime}} N_{j^{\prime}}^1}, \quad \hat{A}_{j k}=\frac{N_{j k}}{N_j} \tag{2.278}\]

我们经常用$N_j$替换$N^1_j$，$N_j$是符号$j$在序列开始时出现的频率。这使我们能够从单个序列中估计参数。

$N_j$ 称为unigram统计，$N_{jk}$称为bigram统计。例如，图2.17显示了字符 {a，…，z，-}（其中-表示空间）的2-gram计数，这是H.G.Wells的《时间机器》一书中估计的。

2.6.3.2 稀疏数据问题

当 $n$ 较大时，拟合n-gram模型时会碰到数据稀疏性的问题，并最终导致过拟合。要看到这一点，请注意，许多估计的计数 $N_{jk}$ 将为$0$，因为现在 $j$ 索引大小为 $K^{n-1}$ 的离散上下文（$j$ 对应的是长度为 $n-1$的序列），这将变得越来越稀疏。即使对于二元语法模型（$n=2$），如果 $K$ 很大，也会出现问题。例如，如果我们的词汇表中有 $K≈50000$ 个单词，那么二元语法模型将有大约25亿个自由参数，对应于所有可能的单词对。我们不太可能在训练数据中看到所有这些配对。然而，我们不想仅仅因为我们碰巧没有在训练文本中看到某个字符串，就预测它完全不可能——这将是一种严重的过拟合[9]¹⁹。

这个问题的“蛮力”解决方案是收集大量数据。例如，谷歌基于从网络中爬取的一万亿个单词拟合了n-gram语法模型（n=1:5）。他们的数据在未压缩时超过100GB，是公开可用的[10]²⁰。尽管这种方法可能会取得惊人的成功（如[HNP09]²¹中所述），但它相当不令人满意，因为人类能够从更少的数据中学习语言（参见[TX00]²²）。

2.6.3.3 MAP 估计

稀疏数据问题的一个简单解决方案是使用具有均匀狄利克雷先验 $\mathbf{A}_{j:} \sim \operatorname{Dir}(\alpha \mathbf{1})$ 的MAP估计。在这种情况下，MAP 估计为

\[\hat{A}_{j k}=\frac{N_{j k}+\alpha}{N_j+K \alpha} \tag{2.279}\]

如果 $\alpha=1$，上式被称为 add-one smoothing。

加法平滑的主要问题是，它假设所有n元语法的可能性都是相等的，这是不太现实的。我们在第3.7.3节讨论了一种基于层次贝叶斯的更复杂的方法。

2.6.4 马尔可夫链的稳态分布

假设我们从马尔可夫链中连续采样样本。在有限状态空间的情况下，我们可以将其视为从一个状态“跳跃”到另一个状态。根据状态转换图，我们倾向于某些状态占据的时间更长。状态的长期分布被称为链的稳态分布（stationary distribution）。在本节中，我们将讨论一些相关理论。在第12章中，我们讨论了一个重要的应用，称为MCMC，它是一种从难以归一化的概率分布中生成样本的方法。在补充材料的第2.2节，我们考虑使用谷歌的PageRank算法对网页进行排名，该算法也利用了稳态分布的概念。

图 $2.18$：一些马尔可夫链。（a） 3-状态非周期链。（b）可还原的4-状态链。

2.6.4.1 什么是稳态分布

设 $A_{i j}=p\left(X_t=j \mid X_{t-1}=i\right)$ 为单步转移矩阵， $\pi_t(j)=p\left(X_t=j\right)$ 为 $t$ 时刻处于状态 $j$ 的概率。

如果我们的初始分布为 $\pi_0$，那么在时间$1$，我们有

\[\pi_1(j)=\sum_i \pi_0(i) A_{i j} \tag{2.280}\]

或者，在矩阵表示法中，$\boldsymbol{\pi}_1=\boldsymbol{\pi}_0 \mathbf{A}$，其中我们假设 $\boldsymbol{\pi}$ 是行向量，因此我们用转移矩阵进行后乘。

现在想象一下迭代这些方程，如果我们达到 $\boldsymbol{\pi}=\boldsymbol{\pi} \mathbf{A}$ 的阶段，那么就说明已经达到了稳态分布（也称为不变分布或平衡分布）。一旦我们进入稳态分布，我们就永远不会脱离这个状态。

例如，考虑图2.18（a）中的链。为了找到它的平稳分布，我们有

\[\left(\begin{array}{lll} \pi_1 & \pi_2 & \pi_3 \end{array}\right)=\left(\begin{array}{lll} \pi_1 & \pi_2 & \pi_3 \end{array}\right)\left(\begin{array}{ccc} 1-A_{12}-A_{13} & A_{12} & A_{13} \\ A_{21} & 1-A_{21}-A_{23} & A_{23} \\ A_{31} & A_{32} & 1-A_{31}-A_{32} \end{array}\right) \tag{2.281}\]

所以 $\pi_1\left(A_{12}+A_{13}\right)=\pi_2 A_{21}+\pi_3 A_{31}$。总的来说，我们有

\[\pi_i \sum_{j \neq i} A_{i j}=\sum_{j \neq i} \pi_j A_{j i} \tag{2.282}\]

换句话说，处于状态 $i$ 的概率乘以流出状态 $i$ 的净流量，必须等于处于状态$j$ 的概率乘以从该状态流入 $i$ 的净流量。这被称为全局平衡方程（global balance equations）。然后，我们可以在约束条件 $\sum_j \pi_j=1$ 下求解这些方程，以找到稳态分布，如下所述。

2.6.4.2 计算稳态分布

为了找到稳态分布，我们需要求解特征向量方程 $\mathbf{A}^{\top} \boldsymbol{v}=\boldsymbol{v}$，然后令 $\boldsymbol{\pi}=\boldsymbol{v}^{\top}$，其中 $\boldsymbol{v}$ 是特征值为 $1$ 的特征向量。（考虑到 $\mathbf{A}$ 是行随机矩阵，所以 $\mathbf{A1}=\mathbf{1}$ 必然成立，换句话说，矩阵 $\mathbf{A}$ 必然存在一个特征值为 $1$ 的特征向量 $\mathbf{1}$；考虑到 $\mathbf{A}$ 和 $\mathbf{A}^\text{T}$ 的特征值是相同的，所以 $\mathbf{A}^\text{T}$ 也存在特征向量 $\mathbf{1}$）当然，由于特征向量本身只在比例上是唯一的（即可以乘以任意非零常数得到相同方向的特征向量），我们必须在最后对 $\boldsymbol{v}$ 进行归一化，以确保它的分量和为 $1$。

然而，请注意，只有当矩阵中的所有项都严格为正时，$A_{ij}>0$，特征向量才保证为实值（因此由于和为 $1$ 的约束，所以 $A_{ij}<1$）。一种更通用的方法可以处理存在转移概率为 $0$ 或 $1$ 的链（如图2.18（a））。 $\pi(\mathbf{I}-\mathbf{A})=\mathbf{0}_{K \times 1}$ 包含 $K$ 个约束和 $\boldsymbol{\pi} \mathbf{1}_{K \times 1}=1$ 包含 $1$ 个约束。因此，我们必须求解 $\boldsymbol{\pi} \mathbf{M}=\boldsymbol{r}$，其中 $\mathbf{M}=[\mathbf{I}-\mathbf{A}, \mathbf{1}]$ 是大小为 $K \times(K+1)$ 的矩阵，$\boldsymbol{r}=[0,0, \ldots, 0,1]$ 是大小为 $1 \times(K+1)$ 的向量。然而，这是 overconstrained 的，因此我们将删除 $\mathbf{M}$ 定义中 $\mathbf{I}-\mathbf{A}$ 的最后一列，并从 $\boldsymbol{r}$ 中删除最后一个$0$。例如，对于3态链，我们必须求解这个线性系统：

\[\left(\begin{array}{lll} \pi_1 & \pi_2 & \pi_3 \end{array}\right)\left(\begin{array}{ccc} 1-A_{11} & -A_{12} & 1 \\ -A_{21} & 1-A_{22} & 1 \\ -A_{31} & -A_{32} & 1 \end{array}\right)=\left(\begin{array}{lll} 0 & 0 & 1 \end{array}\right) \tag{2.283}\]

对于图2.18（a）中的链，我们发现 $\boldsymbol{\pi}=[0.4,0.4,0.2]$。我们可以很容易地验证这是正确的，因为 $\boldsymbol{\pi}=\boldsymbol{\pi} \mathbf{A}$。

不幸的是，并非所有链都有稳态分布，正如我们下面解释的那样。

2.6.4.3 什么时候存在稳态分布

考虑图2.18（b）中的$4$-状态链。如果我们从状态$4$开始，我们将永远停留在那里，因为$4$是一个吸收状态（absorbing state）。因此 $\boldsymbol{\pi}=(0,0,0,1)$ 是一个可能的稳态分布。然而，如果我们从状态 $1$ 或 $2$ 开始，我们将永远在这两个状态之间振荡。所以 $\boldsymbol{\pi}=(0.5,0.5,0,0)$ 是另一个可能的稳态分布。如果我们从状态 $3$ 开始，我们可能会以相等的概率出现在上述任何一个稳态分布中。换句话说，图2.18（b）的转换图存在两个不相交的连通分量。

我们从这个例子中看到，具有唯一稳态分布的必要条件是状态转移图是单连通分量，即我们可以从任何状态转移到任何其他状态。这样的链被称为不可约（irreducible）链。

现在考虑图2.15（a）中的$2$-状态链。只要 $\alpha, \beta>0$，这就是不可约的。假设 $\alpha=\beta=0.9$。通过对称性可以清楚地看出，这条链将在每个状态中花费$50\%$的时间。因此 $\boldsymbol{\pi}=(0.5,0.5)$。但现在假设 $\alpha=\beta=1$。在这种情况下，链将在两个状态之间振荡，但状态的长期分布取决于你从哪里开始。如果我们从状态$1$开始，那么在每个奇数时间步 $(1,3,5, \ldots)$ 上，我们将处于状态$1$；但如果我们从状态$2$开始，那么在每个奇数时间步上，我们都会处于状态$2$。

这个例子激发了以下定义。我们称一个链存在某个极限分布，如果存在 $\pi_j=\lim _{n \rightarrow \infty} A_{i j}^n$ ，并且与所有 $j$ 的起始状态 $i$ 无关。如果这成立，那么长期分布将与起始状态无关：

\[p\left(X_t=j\right)=\sum_i p\left(X_0=i\right) A_{i j}(t) \rightarrow \pi_j \text { as } t \rightarrow \infty \tag{2.284}\]

现在让我们描述一下什么情况存在极限分布。将状态 $i$ 的周期（period）定义为 $d(i) \triangleq \operatorname{gcd}\left\{t: A_{i i}(t)>0\right\}$ ，其中gcd代表最大公约数，即将集合中所有成员分开的最大整数。例如，在图2.18（a）中，我们有 $d(1)=d(2)=\operatorname{gcd}(2,3,4,6, \ldots)=1$ ，$d(3)=\operatorname{gcd}(3,5,6, \ldots)=1$。如果 $d(i)=1$，我们说状态 $i$ 是非周期性的。（确保这一点的充分条件是状态 $i$ 具有自循环，但这不是必要条件。）如果一个链的所有状态都是非周期性的，我们就说它是非周期的。可以得到以下重要结果：

定理2.6.1。每个不可约（单连通）的非周期有限状态马尔可夫链都有一个极限分布，它等于 $\boldsymbol{\pi}$ ，即其唯一的稳态分布。

这个结果的一个特例是，每个正则有限状态链都有一个唯一的平稳分布，其中正则链是指其转移矩阵对于某个整数 $n$ 和所有状态 $i$，$j$ 满足 $A_{i j}^n>0$ 的链，即可以在$n$ 步内从任何状态到任何其他状态。因此，在 $n$ 个步骤之后，链可以处于任何状态，无论它从哪里开始。可以证明，确保正则性的充分条件是链是不可约的（单连通），并且每个状态都有自转换。

为了处理状态空间不有限的马尔可夫链的情况（例如，所有整数的可数集，或所有实数的不可数集），我们需要推广一些早期的定义。由于细节相当技术性，我们只是简要地陈述了主要结论，没有证明。详见[GS92]²³。

为了使平稳分布存在，我们需要不可约性（单连通）和非周期性，如前所述。但我们也要求每个状态都是循环的，这意味着你将以概率 $1$ 返回到那个状态。作为非循环状态（即瞬态）的一个简单示例，考虑图2.18（b）：状态3是瞬态的，因为一旦离开该状态，要么永远围绕状态4旋转，要么永远在状态1和2之间振荡。没有办法回到状态3。

很明显，任何有限状态不可约链都是循环的，因为你总是可以回到起点。但现在考虑一个具有无限状态空间的例子。假设我们对整数 $\mathcal{X}={\ldots,-2,-1,0,1,2, \ldots}$ 执行随机游走。设 $A_{i, i+1}=p$ 为向右移动的概率，$A_{i, i-1}=1-p$ 为向左移动的概率。假设我们从 $X_1=0$ 开始。如果 $p>0.5$ ，我们将向 $+\infty$ 转移；我们不能保证会回来。同样，如果 $p<0.5$，我们将向 $-\infty$ 转移。因此，在这两种情况下，即使链是不可约的，它也不是循环的。如果$p=0.5$，我们可以以概率 $1$ 返回到初始状态，因此该链是循环的。然而，分布在越来越大的整数集上不断扩展，因此预期的返回时间是无限的。导致链没有稳态分布。

更正式地说，如果返回某状态的预期时间是有限的，我们将该状态定义为非空循环（non-null recurrent）状态。我们说，如果一个状态是非周期性的、循环的、非空的，那么它就是可遍历（ergodic）的。我们说，如果一个链的所有状态都是遍历的，那么它就是遍历的。有了这些定义，我们现在可以陈述我们的主要定理：

定理2.6.2。每个不可约的可遍历马尔可夫链都有一个极限分布，它等于 $\boldsymbol{\pi}$ ，即它的唯一平稳分布。

这推广了定理2.6.1，因为对于不可约的有限状态链，所有状态都是循环的且非空的。

2.6.4.4 Detailed balance

建立遍历性可能很困难。我们现在给出一个更容易验证的替代条件。

我们说马尔可夫链 $\mathbf{A}$ 是时间可逆（time reversible）的，如果存在这样的分布$\boldsymbol{\pi}$： $\pi_i A_{i j}=\pi_j A_{j i} \tag{2.285}$ 这被称为细致平衡方程（detailed balance equations）。这意味着从 $i$ 到 $j$ 的流量必须等于从$j$ 到 $i$ 的流量，并由适当的源概率加权。

我们有以下重要结果。

定理2.6.3。如果具有转移矩阵 $\mathbf{A}$ 的马尔可夫链是正则的，并且满足分布 $\boldsymbol{\pi}$ 的细致平衡方程，则 $\boldsymbol{\pi}$ 是链的平稳分布。

证明：要看到这一点，请注意

\[\sum_i \pi_i A_{i j}=\sum_i \pi_j A_{j i}=\pi_j \sum_i A_{j i}=\pi_j \tag{2.286}\]

因此 $\boldsymbol{\pi}=\mathbf{A} \boldsymbol{\pi}$。

请注意，这个条件是充分的，但不是必要的（见图2.18（a），一个不满足细致平衡方程的固定分布链的例子）。

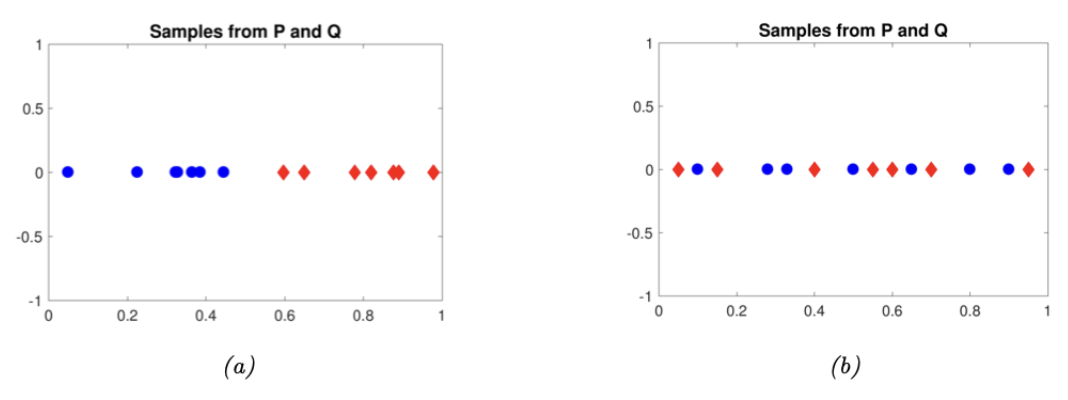
图 $2.19$：来自（a）不同和（b）相似的两个分布的样本。来自[GSJ19]²⁴的图。在亚瑟·格雷顿的善意许可下使用。

2.7 概率分布之间的距离测度

本节，我们将讨论如何衡量两个定义在同一空间内的概率分布 $P$ 和 $Q$ 之间的差距。举例来说，假设分布是以样本的形式定义——$\mathcal{X}=\left\{x_{1, \ldots,} x_N\right\} \sim P$ 和 $\mathcal{X}^{\prime \prime}=\left\{\bar{x}_1, \ldots, \bar{x}_M\right\} \sim Q$。判断样本是否来自于同一个分布的问题被称为 two-sample 检验 （参考图2.19）。为了解决这个问题，我们可以引入某些合适的 divergence metric $D(P,Q)$ ，并且与某个阈值进行比较。（我们使用术语 ‘divergence’ 而不是 ‘distance’，因为我们并不要求 $D$ 是对称的。）假设 $P$ 是数据的经验分布，$Q$ 是通过模型拟合的近似分布。我们可以使用对比 $D(P,Q)$ 和一个阈值来评估模型对数据的近似程度；这被称为 goodness-of-fit 测试。

存在两种主要的方式来对比一对分布：基于$P-Q$ 项 [Sug+13]²⁵ 或者基于 $P/Q$ 项 [SSK12]²⁶ 。接下来我们将介绍这些方案。（部分内容参考了[GSJ19]²⁴）。

2.7.1 $f$-divergence

本节，我们基于两个分布的比率 $r(\boldsymbol{x})=p(\boldsymbol{x}) / q(\boldsymbol{x})$ 来量化两个分布差异。具体而言，使用 $f\mathrm{-divergence}$ [Mor63]²⁷,[AS66]²⁸,[Csi67]²⁹,[LV06]³⁰,[CS04]³¹ ，定义为：

\[D_f(p \| q)=\int q(\boldsymbol{x}) f\left(\frac{p(\boldsymbol{x})}{q(\boldsymbol{x})}\right) d \boldsymbol{x} \tag{2.287}\]

其中 $f: \mathbb{R}_{+} \rightarrow \mathbb{R}$ 是一个凸函数，且满足 $f(1)=0$ 。根据琴森不等式（5.1.2.2节），我们有 $D_f(p | q) \geq 0$，同时 $D_f(p | p)=0$，所以 $D_f$ 是一个有效的散度。接下来我们将讨论一些 $f\mathrm{-divergence}$ 的重要特例。（需要注意的是 $f\mathrm{-divergence}$ 又被称为 $\phi\mathrm{-divergence}$）

图 $2.20$：对于变化的$\alpha$，高斯 $q$ 将 $\alpha$散度最小化为$p$（两个高斯分布的混合）。从[Min05][^MIn05]的图1中可以看出。在Tom Minka的善意许可下使用。

2.7.1.1 KL散度

如果我们令 $f(r)=r \log (r)$。此时我们将得到 Kullback Leibler divergence，定义为：

\[D_{\mathrm{KL}}(p \| q)=\int p(\boldsymbol{x}) \log \frac{p(\boldsymbol{x})}{q(\boldsymbol{x})} d \boldsymbol{x} \tag{2.288}\]

2.7.1.2 Alpha散度

如果 $f(x)=\frac{4}{1-\alpha^2}\left(1-x^{\frac{1+\alpha}{2}}\right)$ ,那 $f\mathrm{-divergence}$ 将变成 alpha 散度 [Ama09]³² ，定义为：

\[D_\alpha^A(p \| q) \triangleq \frac{4}{1-\alpha^2}\left(1-\int p(\boldsymbol{x})^{(1+\alpha) / 2} q(\boldsymbol{x})^{(1-\alpha) / 2} d \boldsymbol{x}\right) \tag{2.289}\]

其中我们假设 $\alpha \neq \pm 1$。另一个常用的参数化方式 [Min05]³³ 定义为：

\[D_\alpha^M(p \| q)=\frac{1}{\alpha(1-\alpha)}\left(1-\int p(\boldsymbol{x})^\alpha q(\boldsymbol{x})^{1-\alpha} d \boldsymbol{x}\right) \tag{2.290}\]

如果令 $\alpha^{\prime}=2 \alpha-1$，则 $D_{\alpha^{\prime}}^A=D_\alpha^M$ 。（我们将使用 2.290 的形式。）

从图2.20可以发现，当 $\alpha \rightarrow-\infty$，$q$ 倾向于匹配 $p$ 的某一个峰值，当 $\alpha \rightarrow \infty$ ,$q$ 倾向于覆盖 $p$ 的所有峰值。更精确地说，当 $\alpha \rightarrow 0$ ，alpha 散度将趋向于 $D_{\mathrm{KL}}(q | p)$。当 $\alpha \rightarrow 1$，alpha 散度将趋向于 $D_{\mathrm{KL}}(p | q)$。当 $\alpha=0.5$，alpha 散度等于 Hellinger 距离（2.7.1.3节）。

2.7.1.3 Hellinger 距离

（Squared）Hellinger 距离定义为：

\[D_H^2(p \| q) \triangleq \frac{1}{2} \int\left(p(\boldsymbol{x})^{\frac{1}{2}}-q(\boldsymbol{x})^{\frac{1}{2}}\right)^2 d \boldsymbol{x}=1-\int \sqrt{p(\boldsymbol{x}) q(\boldsymbol{x})} d \boldsymbol{x} \tag{2.291}\]

这是一个有效的距离度量，因为它是对称，非负的，同时满足三角不等定理。

如果 $f\mathrm{-divergence}$ 中 $f(r)=(\sqrt{r}-1)^2$ ，此时它与 Hellinger 距离等价（相差一个常数项系数），因为

\[\int d \boldsymbol{x} q(\boldsymbol{x})\left(\frac{p^{\frac{1}{2}}(\boldsymbol{x})}{q^{\frac{1}{2}}(\boldsymbol{x})}-1\right)^2=\int d \boldsymbol{x} q(\boldsymbol{x})\left(\frac{p^{\frac{1}{2}}(\boldsymbol{x})-q^{\frac{1}{2}}(\boldsymbol{x})}{q^{\frac{1}{2}}(\boldsymbol{x})}\right)^2=\int d \boldsymbol{x}\left(p^{\frac{1}{2}}(\boldsymbol{x})-q^{\frac{1}{2}}(\boldsymbol{x})\right)^2 \tag{2.292}\]

2.7.1.4 卡方（Chi-squared）距离

卡方距离 $\chi^2$ 定义为

\[\chi^2(p, q) \triangleq \frac{1}{2} \int \frac{(q(\boldsymbol{x})-p(\boldsymbol{x}))^2}{q(\boldsymbol{x})} d \boldsymbol{x} \tag{2.293}\]

如果在 $f\mathrm{-divergence}$ 中令 $f(r)=(r-1)^2$，此时它与上式等价（相差一个常数项系数），因为

\[\int d \boldsymbol{x} q(\boldsymbol{x})\left(\frac{p(\boldsymbol{x})}{q(\boldsymbol{x})}-1\right)^2=\int d \boldsymbol{x} q(\boldsymbol{x})\left(\frac{p(\boldsymbol{x})-q(\boldsymbol{x})}{q(\boldsymbol{x})}\right)^2=\int d \boldsymbol{x} \frac{1}{q(\boldsymbol{x})}(p(\boldsymbol{x})-q(\boldsymbol{x}))^2 \tag{2.294}\]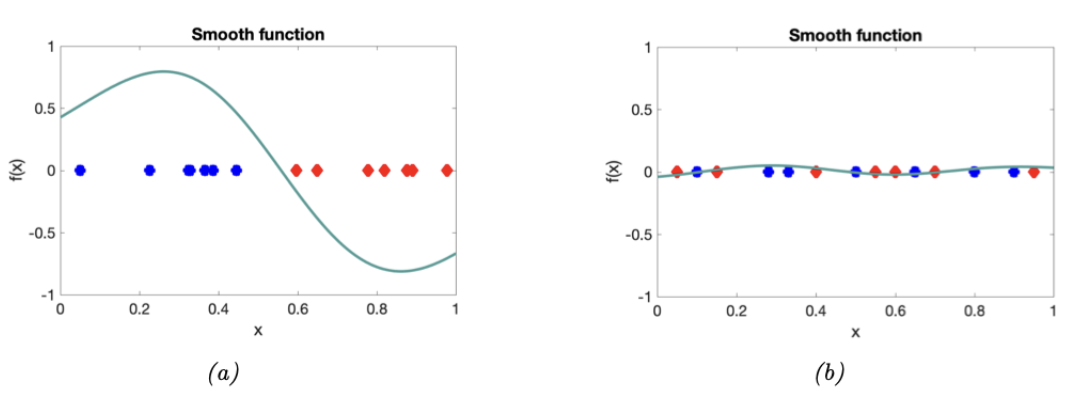

图 $2.21$：一个平滑的witness函数，用于比较（a）不同和（b）相似的两个分布。来自[GSJ19]²⁴的图。在亚瑟·格雷顿的善意许可下使用。

2.7.2 Integral probability metrics

本节，我们将基于 $P-Q$ 定义两个分布之间的距离。使用积分概率度量 （Integral probability metrics，IPM） [Sri+09]³⁴ ，定义为：

\[D_{\mathcal{F}}(P, Q) \triangleq \sup _{f \in \mathcal{F}}\left|\mathbb{E}_{p(\boldsymbol{x})}[f(\boldsymbol{x})]-\mathbb{E}_{q\left(\boldsymbol{x}^{\prime}\right)}\left[f\left(\boldsymbol{x}^{\prime}\right)\right]\right| \tag{2.295}\]

其中 $\mathcal{F}$ 是某类 “平滑”函数。如果函数 $f$ 使得两个期望的差值最大化，则该函数称为 witness function。参照图2.21.

有几种定义函数类 $\mathcal{F}$ 的方式。一种是使用一个 $\mathrm{RKHS}$（Reproducing Kernel Hilbert Space），基于一个正定核函数定义；此时的方法被称为 maximum mean discrepancy 或者 MMD。参考2.7.3节的更多细节。

另一种方式是将 $\mathcal{F}$ 定义所有Lipschitz 连续函数（函数的梯度大小受限）的集合，即 $\mathcal{F}=\left\{\|f\|_L \leq 1\right\}$，其中

\[\|f\|_L=\sup _{\boldsymbol{x} \neq \boldsymbol{x}^{\prime}} \frac{\left|f(\boldsymbol{x})-f\left(\boldsymbol{x}^{\prime}\right)\right|}{\left\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right\|} \tag{2.296}\]

在这种情况下的 IPM 等价于 Wasserstein-1 距离：

\[W_1(P, Q) \triangleq \sup _{\|f\|_L \leq 1}\left|\mathbb{E}_{p(\boldsymbol{x})}[f(\boldsymbol{x})]-\mathbb{E}_{q\left(\boldsymbol{x}^{\prime}\right)}\left[f\left(\boldsymbol{x}^{\prime}\right)\right]\right| \tag{2.297}\]

6.8.2.4 节介绍了更多细节。

2.7.3 MMD

MMD 定义为：

\[\operatorname{MMD}(P, Q ; \mathcal{F})=\sup _{f \in \mathcal{F}:\|f\| \leq 1}\left[\mathbb{E}_{p(\boldsymbol{x})}[f(\boldsymbol{x})]-\mathbb{E}_{q\left(\boldsymbol{x}^{\prime}\right)}\left[f\left(\boldsymbol{x}^{\prime}\right)\right]\right] \tag{2.298}\]

其中 $\mathcal{F}$ 是一个 $\mathrm{RKHS}$，由一个正定核函数 $\mathcal{K}$ 定义。我们可以将这个集合中的函数表示为基础函数的无限和

\[f(\boldsymbol{x})=\langle f, \phi(\boldsymbol{x})\rangle_{\mathcal{F}}=\sum_{l=1}^{\infty} f_l \phi_l(\boldsymbol{x}) \tag{2.299}\]

我们将集合中的 witness 函数限定在这个 RKHS 的单位球内，所以 $|f|{\mathcal{F}}^2=\sum{l=1}^{\infty} f_l^2 \leq 1$。根据期望的线性化，我们有

\[\mathbb{E}_{p(\boldsymbol{x})}[f(\boldsymbol{x})]=\left\langle f, \mathbb{E}_{p(\boldsymbol{x})}[\phi(\boldsymbol{x})]\right\rangle_{\mathcal{F}}=\left\langle f, \boldsymbol{\mu}_P\right\rangle_{\mathcal{F}} \tag{2.300}\]

其中 $\boldsymbol{\mu}_P$ 被称为分布 $P$ 的 kernel mean embedding [Mua+17][^Mua17]。所以

\[\operatorname{MMD}(P, Q ; \mathcal{F})=\sup _{\|f\| \leq 1}\left\langle f, \boldsymbol{\mu}_P-\boldsymbol{\mu}_Q\right\rangle_{\mathcal{F}}=\frac{\boldsymbol{\mu}_P-\boldsymbol{\mu}_Q}{\left\|\boldsymbol{\mu}_P-\boldsymbol{\mu}_Q\right\|} \tag{2.301}\]

因为使内积最大化的单位向量 $\boldsymbol{f}$ 平行于特征均值的差。

为了从直觉上理解，假设 $\phi(x)=\left[x, x^2\right]$。在这种情况下，MMD计算两个分布的前两个矩的差。这可能不足以区分所有可能的分布。然而，使用高斯核相当于比较两个无限大的特征向量，如我们在第18.2.6节中所示，因此我们有效地比较了两个分布的所有矩。事实上，只要我们使用非退化核，就可以证明$\mathrm{MMD}=0$ 的充要条件是 $P=Q$。

2.7.3.2 使用 kernel trick 计算 MMD

本节，我们介绍如何在实践中计算公式（2.301）。给定两个样本集合 $\mathcal{X}=\left\{\boldsymbol{x}_n\right\}_{n=1}^N$ 和 $\mathcal{X}^{\prime}=\left\{\boldsymbol{x}_m^{\prime}\right\}_{m=1}^M$，其中 $\boldsymbol{x}_n \sim P$ ，$x_m^{\prime} \sim Q$。令 $\boldsymbol{\mu}_P=\frac{1}{N} \sum_{n=1}^N \phi\left(\boldsymbol{x}_n\right)$ ，$\boldsymbol{\mu}_Q=\frac{1}{M} \sum_{m=1}^M \phi\left(\boldsymbol{x}_m^{\prime}\right)$ 分别表示两个分布的核均值表征的经验估计。则 squared MMD 由下式计算

\[\begin{align} \operatorname{MMD}^2\left(\mathcal{X}, \mathcal{X}^{\prime}\right) & \triangleq\left\|\frac{1}{N} \sum_{n=1}^N \phi\left(\boldsymbol{x}_n\right)-\frac{1}{M} \sum_{m=1}^M \phi\left(\boldsymbol{x}_m^{\prime}\right)\right\|^2 \tag{2.302} \\ & =\frac{1}{N^2} \sum_{n=1}^N \sum_{n^{\prime}=1}^N \phi\left(\boldsymbol{x}_n\right)^{\top} \phi\left(\boldsymbol{x}_{n^{\prime}}\right)-\frac{2}{N M} \sum_{n=1}^N \sum_{m=1}^M \phi\left(\boldsymbol{x}_n\right)^{\top} \phi\left(\boldsymbol{x}_m^{\prime}\right) \tag{2.303} \\ & +\frac{1}{M^2} \sum_{m=1}^M \sum_{m^{\prime}=1}^M \phi\left(\boldsymbol{x}_{m^{\prime}}^{\prime}\right)^{\top} \phi\left(\boldsymbol{x}_m^{\prime}\right) \tag{2.303} \end{align}\]

考虑到公式（2.303）仅涉及特征向量的内积，我们可以使用核技巧（18.2.5节）对上式进行重写：

\[\operatorname{MMD}^2\left(\mathcal{X}, \mathcal{X}^{\prime}\right)=\frac{1}{N^2} \sum_{n=1}^N \sum_{n^{\prime}=1}^N \mathcal{K}\left(\boldsymbol{x}_n, \boldsymbol{x}_{n^{\prime}}\right)-\frac{2}{N M} \sum_{n=1}^N \sum_{m=1}^M \mathcal{K}\left(\boldsymbol{x}_n, \boldsymbol{x}_m^{\prime}\right)+\frac{1}{M^2} \sum_{m=1}^M \sum_{m^{\prime}=1}^M \mathcal{K}\left(\boldsymbol{x}_m^{\prime}, \boldsymbol{x}_{m^{\prime}}^{\prime}\right) \tag{2.304}\]

2.7.3.3 线性时间复杂度

MMD 的时间复杂度为 $O\left(N^2\right)$ ，其中 $N$ 为每个分布的样本数量。在[Chw+15]³⁵ 中，他们提出了一个不同的检验统计量 非标准化均值表征（unnormalized mean embedding，UME），可以实现 $O(N)$ 的时间复杂度。

其核心思想是仅在测试位置 $\boldsymbol{v}_{1, \ldots,} \boldsymbol{v}_J$ 得到的

\[\text { witness }^2(\boldsymbol{v})=\left(\boldsymbol{\mu}_Q(\boldsymbol{v})-\boldsymbol{\mu}_P(\boldsymbol{v})\right)^2 \tag{2.305}\]

足以发现分布 $P$ 和 $Q$ 之间的差别。所以我们定义（squared）UME 为：

\[\mathrm{UME}^2(P, Q)=\frac{1}{J} \sum_{j=1}^J\left[\boldsymbol{\mu}_P\left(\boldsymbol{v}_j\right)-\boldsymbol{\mu}_Q\left(\boldsymbol{v}_j\right)\right]^2 \tag{2.306}\]

其中 $\boldsymbol{\mu}_P(\boldsymbol{v})=\mathbb{E}_{p(\boldsymbol{x})}[\mathcal{K}(\boldsymbol{x}, \boldsymbol{v})]$ 可以在 $O(N)$ 的时间复杂度下估计得到。

[Jit+16][^Jit16] 中提出了一种UME 的归一化版本—— NME。通过关于位置 $\boldsymbol{v}_j$ 最大化 NME，我们可以最大化测试位置的统计效率，同时找到那些分布 $P$ 和 $Q$ 差别最大的位置。这为高维数据提供一种可解释的 two-sample 检验。

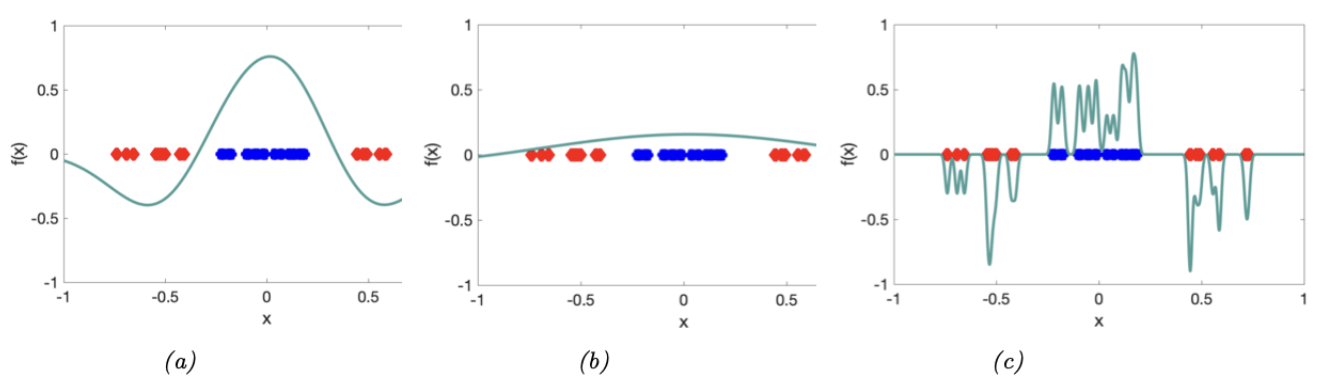
图 $2.22$：减小带宽参数$\sigma$对高斯核定义的witness函数的影响。来自[GSJ19]²⁴的图。在道格·萨瑟兰的善意许可下使用。。

2.7.3.4 选择合适的核函数

MMD（和UME）的有效性很大程度上取决于核函数的正确选择。哪怕是对于1维数据，核函数的选择也十分重要。举例来说，考虑一个高斯核 $\mathcal{K}_\sigma\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\exp \left(-\frac{1}{2 \sigma^2}\left|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right|^2\right)$ 。如图2.22所示，随着 $\sigma$ 的变化，区分两个1维样本是否来自不同集合的能力也随之改变。幸运的是，MMD关于核参数是可微的，所以我们可以选择最优的 $\sigma^2$ 来使得检验效率最大 [Sut+17]³⁶。（参考[Fla+16]³⁷ 中提出的贝叶斯方法，其中最大化核均值表征的GP表征的最大边际似然。）

对于高维数据，比如图片，可以使用一个预训练的CNN模型获取低维表征。举例来说，我们可以定义 $\mathcal{K}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\mathcal{K}_\sigma\left(\boldsymbol{h}(\boldsymbol{x}), \boldsymbol{h}\left(\boldsymbol{x}^{\prime}\right)\right)$ ，其中 $\boldsymbol{h}$ 为CNN的某个隐层，此处的CNN可以是 ‘inception’ 模型 [Sze+15a]³⁸。最后的MMD度量被称为 kernel inception distance **[Bin+18]³⁹。这类似于 **Fréchet inception distance [Heu+17a]⁴⁰，但具备更优的统计属性，且与人的感知判断相关 [Zho+19a][Zho19a]。

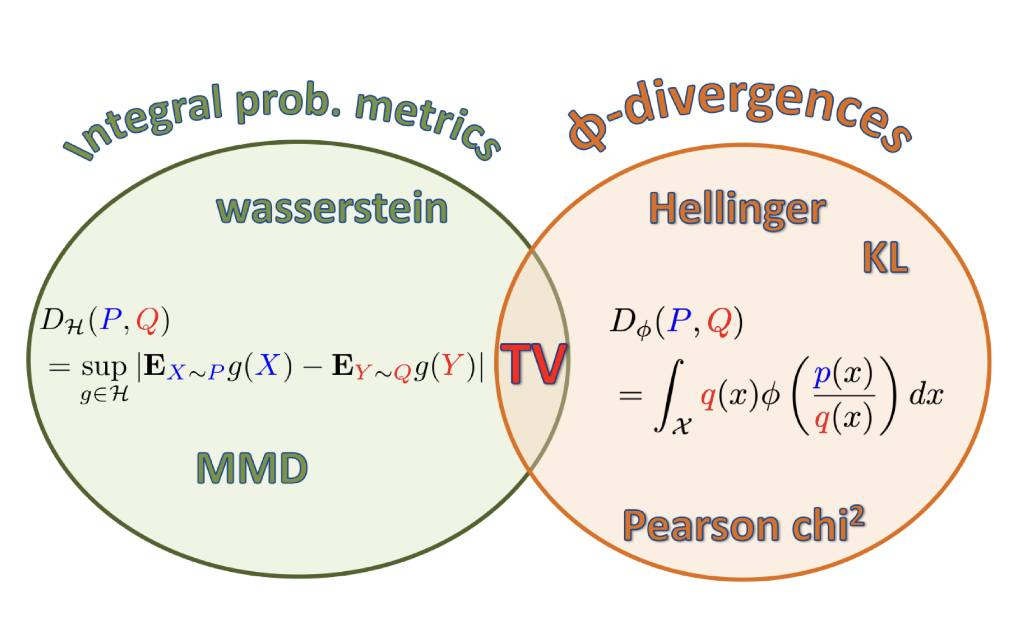
图 $2.23$：两个概率分布$P$和$Q$之间的两种主要散度度量的总结。来自[GSJ19]的图。在亚瑟·格雷顿的善意许可下使用。

2.7.4 全变差距离

两个分布之间的全变差距离（total variation distance）定义为：

\[D_{\mathrm{TV}}(p, q) \triangleq \frac{1}{2}\|\boldsymbol{p}-\boldsymbol{q}\|_1=\frac{1}{2} \int|p(\boldsymbol{x})-q(\boldsymbol{x})| d \boldsymbol{x} \tag{2.307}\]

上式等价于 $f(r)=\lvert r-1 \rvert / 2$ 时的 $f\mathrm{-divergence}$，因为

\[\frac{1}{2} \int q(\boldsymbol{x})\left|\frac{p(\boldsymbol{x})}{q(\boldsymbol{x})}-1\right| d \boldsymbol{x}=\frac{1}{2} \int q(\boldsymbol{x})\left|\frac{p(\boldsymbol{x})-q(\boldsymbol{x})}{q(\boldsymbol{x})}\right| d \boldsymbol{x}=\frac{1}{2} \int|p(\boldsymbol{x})-q(\boldsymbol{x})| d \boldsymbol{x} \tag{2.308}\]

不难发现 TV 距离也是一种积分概率度量。事实上TV距离是仅有的一种既是 IPM 又是 $f\mathrm{-divergence}$ 的散度。参考图2.23的说明。

2.7.5 使用二元分类器估计密度比例

本节，我们将介绍一种简单的方案来对比两个分布，该方法被证明与 IPMs 和 $f\mathrm{-divergence}$ 等价。

考虑一个二分类问题，其中来自分布 $P$ 的样本绑定标签 $y=1$，来自分布 $Q$ 的样本绑定标签 $y=0$，即 $P(\boldsymbol{x})=p(\boldsymbol{x} \mid y=1)$ , $Q(\boldsymbol{x})=p(\boldsymbol{x} \mid y=0)$ 。令 $p(y=1)=\pi$ 表示类别标签的先验分布。根据贝叶斯定理，密度比例 $r(\boldsymbol{x})=P(\boldsymbol{x}) / Q(\boldsymbol{x})$ 由下式给定

\[\begin{align} \frac{P(\boldsymbol{x})}{Q(\boldsymbol{x})} & =\frac{p(\boldsymbol{x} \mid y=1)}{p(\boldsymbol{x} \mid y=0)}=\frac{p(y=1 \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(y=1)} / \frac{p(y=0 \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(y=0)} \tag{2.309}\\ & =\frac{p(y=1 \mid \boldsymbol{x})}{p(y=0 \mid \boldsymbol{x})} \frac{1-\pi}{\pi} \tag{2.310} \end{align}\]

如果我们假设 $\pi=0.5$，我们便可以通过拟合一个二元分类器或者判别器 $h(\boldsymbol{x})=p(y=1 \mid \boldsymbol{x})$，然后计算 $r=h /(1-h)$。这被称为 密度比例估计（density ratio estimation, DRE）技巧。

使用风险最小化，我们可以优化一个分类器 $h$ 。举例来说，如果我们使用 $\mathrm{log-loss}$ ，我们有：

\[\begin{align} R(h) & =\mathbb{E}_{p(\boldsymbol{x} \mid y) p(y)}[-y \log h(\boldsymbol{x})-(1-y) \log (1-h(\boldsymbol{x}))] \tag{2.311} \\ & =\pi \mathbb{E}_{P(\boldsymbol{x})}[-\log h(\boldsymbol{x})]+(1-\pi) \mathbb{E}_{Q(\boldsymbol{x})}[-\log (1-h(\boldsymbol{x}))] \tag{2.312} \end{align}\]

我们也可以使用其他的损失函数 $\ell(y, h(\boldsymbol{x}))$ 实现同样的目标（参考26.2.2节）。

令 $R_{h^*}^{\ell}=\inf _{h \in \mathcal{F}} R(h)$ 表示损失函数 $\ell$ 可获得的最小风险，其中我们在某个函数类 $\mathcal{F}$ 空间内进行最小化。[NWJ09]⁴¹ 表明对于每一个 $f\mathrm{-divergence}$，存在一个损失函数 $\ell$ 使得 $-D_f(P, Q)=R_{h^*}^{\ell}$。举例来说（使用符号 $\tilde{y} \in\{-1,1\}$ 而非 $y \in{0,1}$），全变差距离对应于铰链损失 $\ell(\tilde{y}, h)=\max (0,1-\tilde{y} h)$；Helliinger 距离对应于指数损失 $\ell(\tilde{y}, h)=\exp (-\tilde{y} h)$ ；$\chi^2$散度对应于 logistic 损失 $\ell(\tilde{y}, h)=\log (1+\exp (-\tilde{y} h))$。

我们也可以建立二元分类器与IPMs之间的联系 [Sri+09]³⁴ 。具体而言，令 $\ell(\tilde{y}, h)=-2 \tilde{y} h$，$p(\tilde{y}=1)=p(\tilde{y}=-1)=0.5$。我们有

\[\begin{align} R_{h^*} & =\inf _h \int \ell(\tilde{y}, h(\boldsymbol{x})) p(\boldsymbol{x} \mid \tilde{y}) p(\tilde{y}) d \boldsymbol{x} d \tilde{y} \tag{2.313}\\ & =\inf _h 0.5 \int \ell(1, h(\boldsymbol{x})) p(\boldsymbol{x} \mid \tilde{y}=1) d \boldsymbol{x}+0.5 \int \ell(-1, h(\boldsymbol{x})) p(\boldsymbol{x} \mid \tilde{y}=-1) d \boldsymbol{x} \tag{2.314}\\ & =\inf _h \int h(\boldsymbol{x}) Q(\boldsymbol{x}) d \boldsymbol{x}-\int h(\boldsymbol{x}) P(\boldsymbol{x}) d \boldsymbol{x} \tag{2.315}\\ & =\sup _h-\int h(\boldsymbol{x}) Q(\boldsymbol{x}) d \boldsymbol{x}+\int h(\boldsymbol{x}) P(\boldsymbol{x}) d \boldsymbol{x} \tag{2.316} \end{align}\]

这与式（2.295）匹配。所以分类器扮演跟 witness 函数同样的角色。

以下无正文！！！

image-wechat

↩
↩
↩
↩
↩
↩
↩
↩
↩
↩
↩
↩
↩
↩ ↩²
↩
↩
↩
↩
诺姆·乔姆斯基（Noam Chomsky）[Cho57]⁴²提出的一个不太可能但语法上有效的英语字符串的著名例子是“colourless green ideas sleep furiously”。我们不希望我们的模型预测这个字符串是不可能的。即使是不符合语法的结构，我们的模型也应该以一定的概率允许，因为人们经常违反语法规则，尤其是在口语中。 ↩
See http://googleresearch.blogspot.com/2006/08/all-our-n-gram-are-belong-to-you.html for details. ↩
↩
↩
↩
↩ ↩² ↩³ ↩⁴
↩
↩
↩
↩
↩
↩
↩
↩
↩
↩ ↩²
↩
↩
↩
↩
↩
↩
↩
↩