13 面向非结构数据的神经网络

本章，我们介绍了深度神经网络（$\textrm{DNN}$），深度神经网络的优势在于：通过构建复杂的特征提取器，缓解了手动设计特征的负担，提高了模型的拟合能力。
我们首先介绍了多层感知机模型，它有效解决了传统（单层）感知机模型在解决某些模式识别问题上的不足。

13.1 引言
13.2 多层感知机
13.3 反向传播
13.4 训练神经网络
13.5 正则化
13.6 其他形式的前馈网络
- 13.6.1 径向基函数网络
  - 13.6.1.1 RBF网络用于回归
  - 13.6.1.2 RBF网络用于分类
- 13.6.2 混合专家

13.1 引言

名词对照表
线性回归：linear regression;
逻辑回归: logistic regression;
广义线性模型: generalized linear models;
指数族分布：exponential family distribution;
逆连接函数：inverse link function;
线性(仿射)变换：linear(affine) transformation;
特征变换： feature transformation;
特征提取器： feature extractor.
内容导读
引入了 “$\textrm{DNN}$” 的概念，其背后的动机在于: 通过给于特征提取器更加复杂的结构（更多的可学习参数），提高模型在特征提取方面的能力；
”$\textrm{DNN}$” 又被称为前馈神经网络，所谓前馈神经网络一般是指模型的结构是一个有向无环图。与之对应的是循环神经网络。前馈神经网络中主要包括：（单层）感知机，多层感知机，径向基网络等。

在本书的部分 $\mathrm{II}$，我们讨论了线性模型在回归和分类任务的应用。在第 $\textrm{11}$ 章，我们讨论了线性回归模型$p(y|\mathbf{x}, \mathbf{w})=\mathcal{N}\left(y|\mathbf{w}^{\top}\mathbf{x}, \sigma^{2}\right)$ 。在第 $\textrm{10}$ 章，我们讨论了逻辑回归，其中对于二分类情况，模型定义为 $p(y|\mathbf{x}, \mathbf{w})={\rm{Ber}}(y|\sigma(\mathbf{w}^{\top}\mathbf{x}))$；在多分类任务中，模型定义为 $ p(y|\mathbf{x},\mathbf{w})=\operatorname{Cat}(y|\mathcal{S}(\mathbf{W} \mathbf{x}))$。在第 $\textrm{12}$ 章，我们进一步讨论了广义线性模型，定义为: $p(\mathbf{y}|\mathbf{x};\pmb{\theta})=p(\mathbf{y}|g^{-1}(f(\mathbf{x};\pmb{\theta}))) \tag{13.1}$ 其中 $p(\mathbf{y}|\pmb{\mu})$ 表示均值为 $\pmb{\mu}$ 的指数族分布，$g^{-1}()$ 表示该指数族分布对应的逆连接函数。式中: $f(\mathbf{x};\pmb{\theta})=\mathbf{Wx} + \mathbf{b} \tag{13.2}$ 表示关于输入 $\mathbf{x}$ 的一个线性（仿射）变换函数，其中 $\mathbf{W}$ 表示权重 ($\textrm{weights}$)，$\mathbf{b}$ 表示偏置 ($\textrm{biases}$)。

在线性模型中，我们依然假设输出与输入 $\mathbf{x}$ 呈线性关系，该假设具有很强的局限性。为了增加此类线性模型的灵活性，一种简单方法是使用特征变换，即利用 $\phi(\mathbf{x})$ 替代 $\mathbf{x}$。比如我们可以使用多项式变换。具体而言，对于 $\textrm{1}$ 维数据，特征变换函数可以定义为 $\phi(x)=[1,x,x^2,x^3,…]$，我们在 $\textrm{1.2.2.2}$ 节中对该方法进行了讨论。这种方法有时被称为 基函数拓展 ($\textrm{basis function expansion}$)。在特征变换的基础上，式 $13.2$ 可以定义为: $f(\mathbf{x}; \pmb{\theta})=\mathbf{W}\mathbf{\phi}(\mathbf{x}) + \mathbf{b} \tag{13.3}$ 需要注意的是，上述模型的输出关于参数 $\pmb{\theta}=(\mathbf{W}, \mathbf{b})$ 依然是线性关系，这样可以降低了模型的拟合难度。然而，手动设计的特征变换函数依然具有很强的局限性。

一个很自然的泛化是为特征提取器赋予自己的参数 $\pmb{\theta}^\prime$，即: $f(\mathbf{x};\pmb{\theta},\pmb{\theta}^\prime)=\mathbf{W}\phi(\mathbf{x};\pmb{\theta}^\prime)+\mathbf{b} \tag{13.4}$ 我们可以递归地重复上述过程，从而构造一个越来越复杂的函数。如果我们组合 $L$ 个函数，即 $f(\mathbf{x};\pmb{\theta})=f_L(f_{L-1}(...(f_1(\mathbf{x}))...))\tag{13.5}$ 其中 $f _l(\mathbf{x})=f(\mathbf{x};\pmb{\theta} _l)$ 为第 $l$ 层的函数。这便是 深度神经网络 ($\textrm{deep neural networks, DNNs}$) 背后的关键思想。

术语 “$\textrm{ DNN}$ ” 实际上包含了一大类模型，这类模型的特点在于它们都是将多个可微函数组合成任何类型的 $\textrm{DAG}$（有向无环图），从而实现输入到输出的映射函数的建模，式 $13.5$ 是其中的最简单的一个例子，它的 $\textrm{DAG}$ 是一个链式结构。“$\textrm{ DNN}$ ”又被称为 前馈神经网络（$\textrm{feedforward neural network, FFNN}$）或 多层感知机（$\textrm{multilayer perceptron, MLP}$）。

$\textrm{MLP}$ 假定输入是一个维度固定的矢量，即 $\mathbf{x} \in \mathbb{R}^D$。我们称此类数据为“非结构化数据” ($\textrm{unstructured data}$)，因为我们没有对输入的形式作任何假设。但是，$\textrm{MLP}$ 很难应用于具有可变大小或形状的输入。在第 $\textrm{14}$ 章中，我们将讨论卷积神经网络（$\textrm{convolutional neural networks, CNN}$），用于处理可变大小的图像。在第 $\textrm{15}$ 章中，我们将讨论递归神经网络（$\textrm{recurrent neural networks, RNN}$），用于处理可变长度的序列。在第 $\textrm{23}$ 章中，我们将讨论图神经网络（$\textrm{graph neural networks, GNN}$），用于处理可变形状的图数据。有关 $\textrm{DNN}$ 的更多信息，可参考其他书籍 [$\textrm{HG20}$]¹, [$\textrm{Zha19a}$]², [$\textrm{Ger19}$]³。

13.2 多层感知机

名词对照表
不可微: non-differentiable
优化器：optimizer
内容导读
传统感知机模型并不能有效解决 $\textrm{XOR}$ 这一模式识别问题;
多层感知机 $\textrm{MLP}$ 可以有效解决上述难点，但其所包含的不可微的单位阶跃激活函数限制了其被大规模使用的可能;
通过使用可微的非线性激活函数，可以有效改善上述问题，但应避免使用存在饱和区的激活函数（会导致梯度消失的问题）。

在第 $\textrm{10.2.5}$ 节，我们介绍了 感知机 ($\textrm{perceptron}$) 模型，它实际上就是逻辑回归模型的一个确定性版本（$\textrm{deterministic version}$）。具体而言，它是一个具备如下形式的映射函数: $f(\mathbf{x};\mathbf{\theta})=\mathbb{I}(\mathbf{w}^{\rm{T}}\mathbf{x}+b\ge0)=H(\mathbf{w}^{\rm{T}}\mathbf{x}+b) \tag{13.6}$ 其中 $H(a)$ 表示 单位阶跃函数（$\textrm{heaviside step function}$），又被称为 线性阈值函数 ($\textrm{linear threshold function}$）。由于感知机模型的决策边界依然是线性的，所以表达能力十分有限。$\textrm{1969}$ 年，$\textrm{Marvin Minsky}$ 和 $\textrm{Seymour Papert}$ 出版了一本名为 $\textrm{《 Perceptrons》}$ [$\textrm{MP69}$]⁴ 的著作，书中列举了许多感知机无法解决的模式识别问题。在讨论如何解决这些问题之前，我们首先分析其中的一个具体示例。

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	0

表$13.1$：抑或问题的真值表，$y=x _{1} \underline{\vee} x _{2}$。

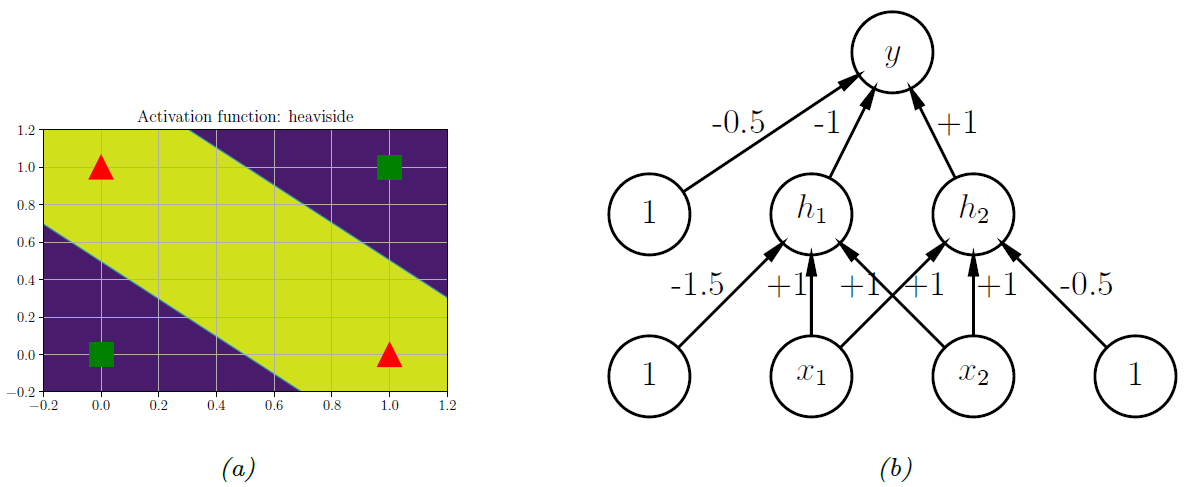
xor-heaviside

图 $13.1$：$\textrm{(a)}$ 抑或函数无法实现线性可分，但基于单位阶跃函数构建的两层模型可以将数据分开。程序由 $xor-heaviside.py$ 生成。 $\textrm{(b)}$ 包含一个隐藏层的神经网络，其中的权重由人工设计，该网络实现了抑或函数。 $h_1$ 表示 $AND$ 函数，$h_2$ 表示 $OR$ 函数。偏置项表示为常数节点（值为 $\textrm{1}$）的连接权重。

  
import numpy as np
# Show that 2 layer MLP (with manually chosen weights) can solve the XOR problem
# xor-heaviside.py
import numpy as np
import matplotlib.pyplot as plt
def heaviside(z):
    return (z >= 0).astype(z.dtype)
def mlp_xor(x1, x2, activation=heaviside):
    return activation(-activation(x1 + x2 - 1.5) + activation(x1 + x2 - 0.5) - 0.5)
x1s = np.linspace(-0.2, 1.2, 100)
x2s = np.linspace(-0.2, 1.2, 100)
x1, x2 = np.meshgrid(x1s, x2s)

z1 = mlp_xor(x1, x2, activation=heaviside)
z2 = mlp_xor(x1, x2, activation=sigmoid)

plt.figure()
plt.contourf(x1, x2, z1)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "r^", markersize=20)
plt.title("Activation function: heaviside", fontsize=14)
plt.grid(True)
plt.show()

13.2.1 抑或问题

$\textrm{《 Perceptrons》}$书中最著名的例子之一就是 $\textrm{XOR}$ 问题。在该示例中，我们的目标是学习一个函数，用于计算两个二进制输入的异或值。表 $\textrm{13.1}$ 给出了该函数的真值表。我们在图 $\textrm{13.1a}$ 中对真值表进行了可视化。显然，其中的数据并不是线性可分离的，因此感知机模型无法实现对该映射函数的建模。

但是，我们可以通过叠加多个感知机模型来克服这个难点，即 多层感知机（$\textrm{multilayer perceptron, MLP}$）。例如，要解决 $\textrm{XOR}$ 问题，我们可以使用图 $\textrm{13.1b}$ 所示的 $\textrm{MLP}$。它由 $\textrm{3}$ 个感知机组成，分别为 $h_1$，$h_2$ 和 $y$。节点 $x$ 表示输入，节点 $1$ 表示常数项，节点 $h_1$ 和 $h_2$ 被称为 隐藏单元 （$\textrm{hidden units}$），因为在训练数据中未观察到它们的真值。

第一个隐藏单元利用合理设置的权重来计算 $h_{1}=x_{1} \wedge x_{2}$（ $\wedge$ 表示 $\rm{AND}$ 操作）。具体而言，它的输入为 $x_1$和 $x_2$，且权重均为 $\textrm{1.0}$，同时具有 $\textrm{-1.5}$ 的偏置项（通过虚设一个常量节点 $\textrm{1}$ 来模拟偏置项）。因此，如果 $x_1$ 和 $x_2$ 都等于 $\textrm{1}$，则 $h_1$ 将被激活，因为 $\mathbf{w}_1^{\rm{T}}\mathbf{x}-b_1=[1.0, 1.0]^{\rm{T}}[1, 1] - 1.5 =0.5 > 0 \tag{13.7}$ 类似的，第二个隐藏单元计算 $h_{2}=x_{1} \vee x_{2}$，其中 $\vee$ 为 $\rm{OR}$ 操作，第三个节点计算输出 $y=\overline{h_1} \wedge h_2$，其中 $\bar{h}=\neg h$ 为 $\rm{NOT}$ 操作（逻辑非）。所以节点 $y$ 表示为 $y=f\left(x_{1}, x_{2}\right)=\overline{\left(x_{1} \wedge x_{2}\right)} \wedge\left(x_{1} \vee x_{2}\right) \tag{13.8}$ 上式等价于 $\rm{XOR}$ 函数。

将上述案例一般化， $\textrm{MLP}$ 可以用来表示任何逻辑函数。但是，我们显然希望避免手动设置权重和偏置。在本章的其余部分，我们将讨论从数据中学习这些参数的方法。

13.2.2 可微多层感知机

我们在第 $\textrm{13.2.1}$ 节中讨论的 $\textrm{MLP}$ 被定义为多个感知机的叠加，每个感知机都包含不可微的 $\textrm{Heaviside}$ 函数。这使得模型很难训练，这就是为什么它们从未被广泛使用的原因。然而，如果我们将阶跃函数 $H:\mathbb{R}\rightarrow {0,1}$ 替换为一个可微的 激活函数 （$\textrm{activation function}$）$\varphi:\mathbb{R} \rightarrow \mathbb{R}$ 。：更准确地说，我们将每层 $l$ 的隐藏单元 $\mathbf{z}_l$ 定义为通过这个激活函数进行逐元素传递的前一层的隐藏单元的线性变换的结果。

More precisely, we define the hidden units $\mathbf{z}_l$ at each layer $l$ to be a linear transformation of the hidden units at the previous layer passed elementwise through this activation function.

\[\mathbf{z}_l=f_l(\mathbf{z}_{l-1})=\varphi(\mathbf{b}_l+\mathbf{W}_l\mathbf{z}_{l-1}) \tag{13.9}\]

或者，以标量的形式表示为：

\[z_{kl}=\varphi_l \left( b_{kl}+\sum_{j=1}^{K_{l-1}}w_{jkl}z_{jl-1} \right) \tag{13.10}\]

如式 $ 13.5$ 所示，如果我们现在将 $L$ 个诸如此类的激活函数叠加在一起，然后使用链式规则，计算输出关于每一层中参数的梯度，也称为 反向传播 （$\textrm{backpropagation}$），如我们在第 $\textrm{13.3}$ 节中所解释的。（这对于任何一种可微的激活函数都是可行的，尽管某些类型的激活函数要比其他类型的函数更适用，正如我们在第 $\textrm{13.2.3}$ 节中讨论的那样）。然后，我们可以将梯度传递给优化器，从而最小化某些训练目标，正如我们在 $\textrm{13.4}$ 节讨论的那样。因此，术语“$\textrm{ MLP}$”几乎总是指可微的模型，而不是指具有不可微的线性阈值单位的历史版本。

$\textrm{Name}$	$\textrm{Definition}$	$\textrm{Range}$	$\textrm{Reference}$
$\textrm{Sigmoid}$	$\sigma_{a}=\frac{1}{1+e^{-a}}$	$[0, 1]$
$\textrm{Hyperbolic tangent}$	$\tanh(a)=2\sigma(2a)-1$	$[-1, 1]$
$\textrm{Softplus}$	$\sigma_{+}(a)=\log(1+e^a)$	$[0, \infty]$	[GBBB11]⁵
$\textrm{Rectified linear unit}$	$\operatorname{ReLU}(a)=\max (a, 0)$	$[0, \infty]$	[GBB11]⁵;[KSH12]⁶
$\textrm{Leaky ReLU}$	$\max (a, 0)+\alpha \min (a, 0)$	$[-\infty, +\infty]$	[MHN13]⁷
$\textrm{Exponential linear unit}$	$\max (a, 0)+\min \left(\alpha\left(e^{a}-1\right), 0\right)$	$[-\infty, +\infty]$	[CUH16]⁸
$\textrm{Swish}$	$a \sigma(a)$	$[-\infty, +\infty]$	[RZL17]⁹

表 $\textrm{13.2}$：神经网络中常用的一些激活函数

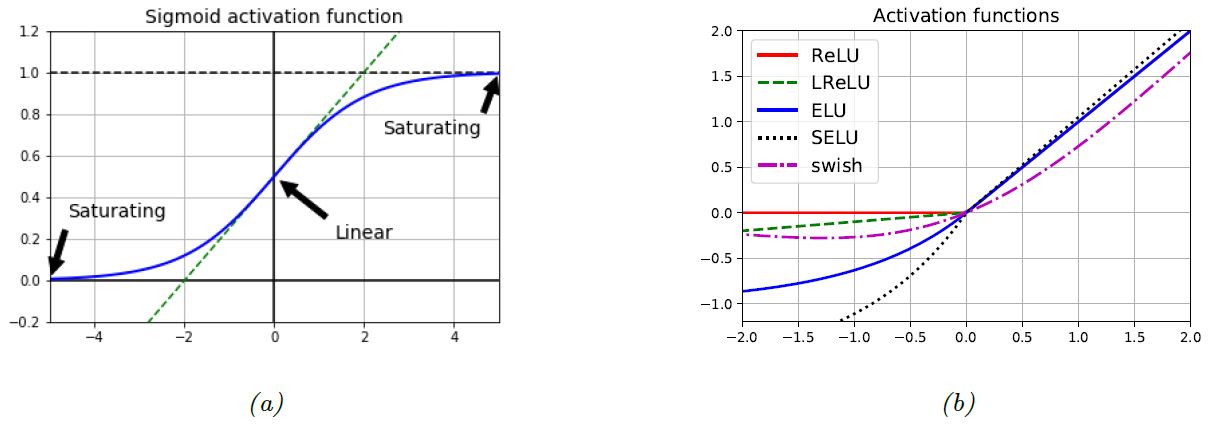
activations

图 $\textrm{13.2}$：$\textrm{(a)}$ 对于 $sigmoid$ 函数而言，当输入在 $0$ 附近时，输出与输入呈线性关系，但对于较大的正值或负值输入，则输出存在饱和区。图形由程序生成。 $\textrm{(b)}$ 一些常用的非饱和激活函数的可视化。图形由程序生成。

13.2.3 激活函数

我们可以在每一层使用任何一种可微的激活函数。然而，如果我们使用线性（$\textrm{linear}$）激活函数 $\varphi_l(a)=c_la$，那整个模型将退化为一个常规的线性模型。以式 $13.5$ 为例，该模型将退化为：

\[f(\mathbf{x};\mathbf{\theta})=\mathbf{W}_Lc_L(\mathbf{W}_{L-1}c_{L-1}(...(\mathbf{W}_1\mathbf{x})...)) \propto \mathbf{W}_L\mathbf{W}_{L-1}...\mathbf{W}_1\mathbf{x}=\mathbf{W}^\prime\mathbf{x} \tag{13.11}\]

在上式中，为了符号上的简洁性，我们丢弃了偏置项。基于上述原因，使用非线性激活函数就显得十分重要。

在神经网络发展的早期阶段，通常会使用 $\textrm{S}$ 型 ($\textrm{logistic}$) 激活函数，该函数可以看做是单位阶跃函数的平滑近似版本。然而，如图 $\textrm{13.2a}$ 所示，对于较大的正值输入，$\textrm{S}$ 形函数存在饱和输出 $\textrm{1}$；对于较大的负值输入，$\textrm{S}$ 形函数存在饱和输出 $\textrm{0}$。 $\textrm{tanh}$ 激活函数具有相似的形状，但其饱和输出分别为 $\textrm{-1}$ 和 $\textrm{+1}$。在这些饱和区域，输出关于输入的斜率将接近于零。因此，如我们在第 $\textrm{13.4.2}$ 节中所讨论的，来自深层网络的任何梯度信号都将“消失”。

要想成功训练一个非常深的神经网络模型，一个关键因素是使用 非饱和激活函数 （$\textrm{non-saturating activation functions}$）。几种不同的激活函数如表 $\textrm{13.2}$ 所示。其中最常用的是 整流线性单元 （$\textrm{rectifled linear unit, ReLU}$）。定义为

\[{\rm{ReLU}}(a)=\max(a,0)=a\mathbb{I}(a>0) \tag{13.12}\]

该 $\textrm{ReLU}$ 函数简单地将负值输入置零，并保持正值输入保持不变。如 $\textrm{13.3.3.2}$ 节所介绍的，这种形式至少保证对于正值输入，梯度的值为 $\textrm{1}$，从而缓解了梯度消失的问题。

不幸的是，对于负值输入，$\textrm{ReLU}$ 的梯度依然为 $\textrm{0}$，因此，该单元将永远无法获得任何反馈信号来帮助其摆脱当前的参数设置（译者注：即无法逃离负值区域）；这被称为 “$\pmb{\textrm{dying ReLU}}$” 问题。

一种简单的解决方法是使用 [$\textrm{MHN13}$]⁷ 中提出的 $\pmb{\textrm{leaky ReLU}}$。定义为

\[{\rm{LReLU}}(a;\alpha)=\max(\alpha a,a) \tag{13.13}\]

其中 $0 \lt \alpha \lt 1$。该函数对于正值输入的斜率为 $\textrm{1}$，对于负值输入的斜率为 $\alpha$，所以可以确保当输入为负值时，依然可以有信号可以从更深的网络层中反传回来。如果我们允许参数 $\alpha$ 是可学习而非固定的， $\pmb{\textrm{leaky ReLU}}$ 将被称为 $\pmb{\textrm{parametric ReLU}}$。

另一个普遍的选择是 [$\textrm{CUH16}$]⁸ 中提出的 $\textrm{ELU}$，定义为

\[{\rm{ELU}}(a;\alpha) = \begin{cases} \alpha(e^a-1) & \text{if } a\le0\\ a & \text{if } a \gt 0 \end{cases} \tag{13.14}\]

与 $\pmb{\textrm{leaky ReLU}}$ 相比，它具有平滑函数的优点。

在 [$\textrm{Kla+17}$]¹⁰ 中提出了一种 $\textrm{ELU}$ 的变体，称为 $\pmb{\textrm{SELU}}$（$\textrm{self-normalizing ELU}$）。定义为

\[{\rm{SELU}}(a;\alpha,\lambda)=\lambda{\rm{ELU}}(a;\alpha) \tag{13.15}\]

令人惊讶的是，他们证明了通过精心为 $\alpha$ 和 $\lambda$ 设置合理的值，即使不使用 $\textrm{batchnorm}$ 技术（见 $\textrm{13.4.5}$节），也可以确保通过激活函数来使每个网络层的输出是被标准化的（假设输入也已标准化），从而加快模型的拟合速度。

作为手动发现良好的激活函数的替代方法，我们可以使用黑盒优化方法来对激活函数空间进行搜索。 [$\textrm{RZL17}$]⁹ 使用这种方法发现了被称为 $\mathrm{swish}$ 的函数，该函数在某些图像分类数据集上似乎表现很好。该函数定义为

\[{\rm{swish}}(a;\beta)=a\sigma(\beta a)\tag{13.16}\]

有关这些激活函数的可视化对比，请参见图 $\textrm{13.2b}$。我们发现，不同的激活函数主要是在处理负值输入的方式上存在差异。

13.2.4 案例模型

名词对照表
嵌入矩阵: embedding matrix
词嵌入: word embedding
微调: fine-tune
分类分布： categorical distribution
内容总结
介绍了 $\textrm{MLP}$ 在不同类型数据以及不同任务上的应用实例。

$\textrm{MLPs}$ 可以对很多类型的数据进行分类和回归，接下来我们将给出一些案例。

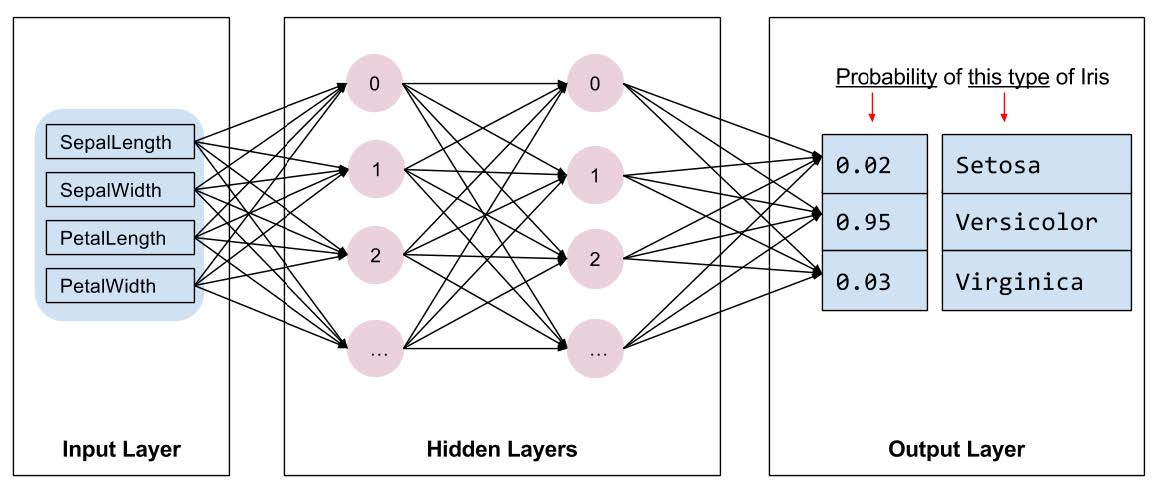
mlpIris

图 $\textrm{13.3}$：一个简单的用于鸢尾花分类问题的 $2$ 层 $\textrm{MLP}$。隐藏层中的节点代表隐藏单元 $h _{1,i}$ 和 $h _{2,j}$，节点间的边代表权重 $w _{2,i,j}$ ，其中 $2$ 表示第二层。（第一层的权重矩阵对应于 $\textrm{input-to-hidden}$ 映射。）所以$\mathbf{z} _{2}=\varphi _{2}(\mathbf{W} _{2} \mathbf{z} _{1}+\mathbf{b} _{1})$ ，尽管为了表达上的简洁，我们省略了偏置项。

13.2.4.1 MLP用于表格数据分类

图 $\textrm{13.3}$ 给出了一个包含两个隐藏层的 $\textrm{MLP}$ 示意图，将该 $\textrm{MLP}$ 应用于 $\textrm{1.2.1.1}$ 节中的表格鸢尾花数据集，该数据集具有 $\textrm{4}$ 个特征和 $\textrm{3}$ 个类别。该模型具有如下形式

\[\begin{align} p(y|\mathbf{x};\mathbf{\theta})=& {\rm{Cat}}(y|f_3(\mathbf{x};\mathbf{\theta})) \tag{13.17}\\ f_3(\mathbf{x};\mathbf{\theta})=&\mathcal{S}(\mathbf{W}_3f_2(\mathbf{x};\mathbf{\theta})+\mathbf{b}_3) \tag{13.18} \\ f_2(\mathbf{x};\mathbf{\theta})=&\varphi_2(\mathbf{W}_2f_1(\mathbf{x};\mathbf{\theta})+\mathbf{b}_2) \tag{13.19} \\ f_1(\mathbf{x};\mathbf{\theta})=&\varphi_1(\mathbf{W}_1f_0(\mathbf{x};\mathbf{\theta})+\mathbf{b}_1) \tag{13.19} \\ f_0(\mathbf{x};\mathbf{\theta})=&\mathbf{x} \tag{13.21} \end{align}\]

其中 $\mathbf{\theta}=(\mathbf{W}_3,\mathbf{b}_3,\mathbf{W}_2,\mathbf{b}_2,\mathbf{W}_1,\mathbf{b}_1)$ 为模型中的参数，对应于 $\textrm{3}$ 组可调节权重的边。我们看到最终（输出）层的激活函数为 $\textrm{softmax}$ 函数，$\textrm{softmax}$ 函数是分类分布的反向连接函数。对于隐藏层，我们可以自由选择 $13.2.3$ 节中介绍的不同形式的激活函数。

mlpMnist

图 $\textrm{13.4}$：用于$\textrm{MNIST}$ 分类的 $\textrm{MLP}$ 结构。需要注意的是模型的参数量 $100,480=(784+1)\times128$, $16,512=(128+1)\times 128$。

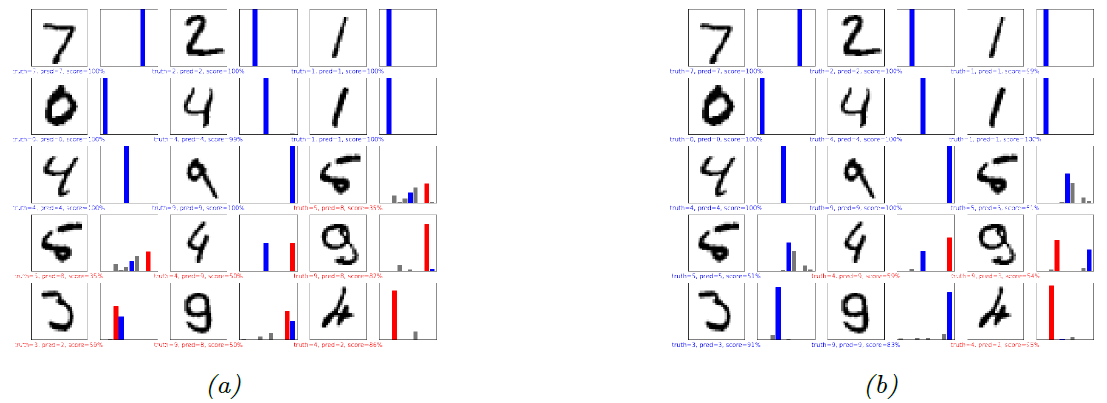
mnistResult

图 $\textrm{13.5}$：基于 $\textrm{MLP}$（包含$2$个隐藏层和$1$个输出层，隐藏层含$128$个节点，输出层包含$10$个节点）对一些 $\textrm{MNIST}$ 图片的分类结果。红色为错误预测，蓝色为正确预测。$\textrm{(a)}$ 训练 $1$ 个周期。 $\textrm{(b)}$ 训练 $2$ 个周期。

13.2.4.2 MLP用于图像分类

要将 $\textrm{MLP}$ 应用于图像分类，我们需要将 $\textrm{2d}$ 输入“展开”（$\textrm{flatten}$）为 $\textrm{1d}$ 向量。然后，我们可以使用类似于第$\textrm{13.2.4.1}$ 节中所述的前馈网络。例如，考虑构建一个 $\textrm{MLP}$ 以对 $\textrm{MNIST}$ 数字进行分类（第$\textrm{3.7.2}$ 节）。这些数字图片表示为 $28\times28 = 784$ 维的向量。如果我们使用 $\textrm{2}$ 个具有 $\textrm{128}$ 个单元的隐藏层，和 $\textrm{1}$ 个包含 $\textrm{10}$ 个输出单元的 $\textrm{softmax}$ 层，将得到如图 $\textrm{13.4}$ 所示的模型。

我们在图 $\textrm{13.5}$ 中展示了一些该模型的预测结果。我们对训练集仅训练两个“周期”（$\textrm{epochs}$, 遍历数据集的次数），但是该模型已经具备了较好的性能，测试集的准确率为 $\textrm{97.1％}$。此外，预测错误的案例似乎也是可以理解的，例如将 $\textrm{9}$ 误分类为 $\textrm{3}$。训练更多的时间可以进一步提高模型的测试精度。

在第 $\textrm{14}$ 章中，我们将讨论另一种称为卷积神经网络的模型，该模型更适用于图像数据的处理。通过利用与图像数据空间结构相关的先验知识，它可以获得更好的性能，并使用更少的参数。相比之下，$\textrm{MLP}$ 对输入的排列具有不变性。换句话说，我们可以随机地对像素进行排列，并且可以获得相同的结果（前提是我们对所有的输入使用相同的随机排列算法）。

In Chapter $14$ we discuss a different kind of model, called a convolutional neural network, which is better suited to images. This gets even better performance and uses fewer parameters, by exploiting prior knowledge about the spatial structure of images. By contrast, the MLP is invariant to a permutation of its inputs. Put another way, we could randomly shuffle the pixels and we would get the same result (assuming we use the same random permutation for all inputs).

mlpIMDB

图 $\textrm{13.6}$：用于 $\textrm{IMDB}$ 分类的 $\textrm{MLP}$ 结构。语料库大小为 $V=1000$，嵌入层大小为 $E = 16$。嵌入矩阵 $\mathbf{W}_1$ 大小为 $10,000\times16$，隐藏层（$\textrm{dense}$）的权重矩阵 $\mathbf{W}_2$ 大小为 $16 \times 16$ ，偏置 $\mathbf{b}_2$ 大小为 $16$（$16 \times 16 + 16 = 272$），最后一层（$\textrm{dense_1}$）的权重矩阵 $\mathbf{w}_3$ 大小为 $16$，偏置 $b_3$ 大小为 $1$。全局平均池化不包含参数。

13.2.4.3 MLP用于电影评论的情感分析

[$\textrm{Maa+11}$]¹¹ 中提出的 $\textrm{IMDB}$ 电影评论数据集（$\textrm{IMDB}$ 表示 $\textrm{internet movie database}$）被称为 “文本分类界的 $\textrm{MNIST}$”。该数据集包含 $\textrm{25k}$ 带有标签的样本用于训练，另外 $\textrm{25k}$ 的样本用于测试。每个样本都有一个二进制标签，代表积极或消极的评分。此任务被称为（二进制）情感分析 （$\textrm{sentiment analysis}$）。例如，以下是训练集中的两个样本：

this film was just brilliant casting location scenery story direction everyone’s really suited the part they played robert <UNK> is an amazing actor …
big hair big boobs bad music and a giant safety pin these are the words to best describe this terrible movie i love cheesy horror movies and i’ve seen hundreds…

显然，第一个样本的标签为正例（积极评价），第二个为负例（消极评价）。

我们可以设计一个 $\textrm{MLP}$ 实现情感分析。不妨假设输入是一个包含 $T$ 个符号（$\textrm{token}$）的序列 $\textbf{x} _{1:T}$，其中 $\textbf{x} _t$ 是一个长度为 $ V $ 的 $ \textrm{one-hot} $ 向量， $V$ 为语料库的大小，我们将这种编码方式称为无序的单词袋（第 $10.4.3.1$ 节）。模型的第一层为 $E\times V$ 的嵌入矩阵 $\textbf{W} _1 $，该层将每一个稀疏的 $V $ 维向量映射到一个稠密的 $E $ 维向量 $\mathbf{e} _t=\mathbf{W} _1 \mathbf{x} _t $（ $19.5$ 节介绍了更多关于词嵌入的细节）。接着我们使用 全局平均池化（$\textrm{global average pooling}$）将 $T\times D $ 的序列嵌入向量转化为一个固定长度的向量 $\overline{\mathbf{e}}=\frac{1}{T}\sum _{t=1}^T \mathbf{e} _t $ 。最后我们将该向量传入一个非线性隐藏层，得到一个 $K $ 维向量 $\mathbf{h} $，并将其传入最后的线性 $\textrm{logistic} $ 层。综上所述，模型定义如下： $\begin{align} p(y|\mathbf{x};\mathbf{\theta}) = & {\rm{Ber}}(y|\sigma(\mathbf{w}_3^{\rm{T}}\mathbf{h}+b_3)) \tag{13.22} \\ \mathbf{h}= & \varphi(\mathbf{W}_2{\rm{\bar{\mathbf{e}}}}+\mathbf{b}_2) \tag{13.23} \\ {\bar{\mathbf{e}}}=& \frac{1}{T}\sum_{t=1}^T\mathbf{e}_t \tag{13.24} \\ \mathbf{e}_t=& \mathbf{W}_1\mathbf{x}_t \tag{13.25} \end{align}$

如果我们令语料库大小为 $V = 1000$，嵌入向量维度为 $E = 16$，隐藏层的维度为 $\textrm{16}$，则得到的模型如图 $\textrm{13.6}$ 所示。最终的模型在验证集的准确度为 $\textrm{86％}$。

我们发现模型中大多数参数都分布在嵌入矩阵中，这可能会导致过拟合问题。幸运的是，正如我们在第 $\textrm{19.5}$ 节中讨论的那样，我们可以使用无监督预训练方法得到的词嵌入，然后我们只需要在特定任务上对输出层的参数进行微调即可。

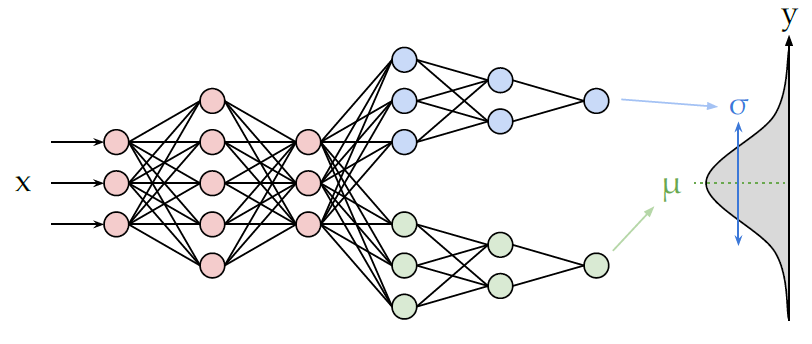
mlpHeter

图 $\textrm{13.7}$：$\textrm{MLP}$ 包含一个共享的主干网络和两个输出头，一个用于预测期望，另一个用于预测方差。

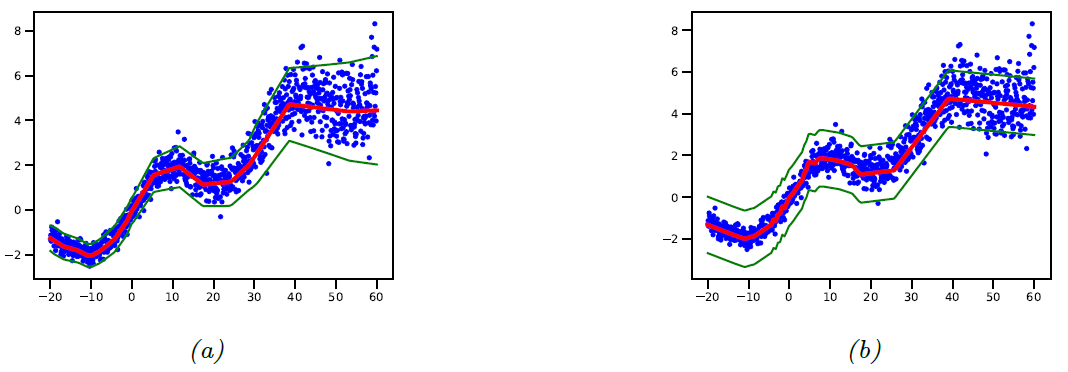
heterResult

图 $\textrm{13.8}$：使用 $\textrm{MLE}$ 的 $\textrm{MLP}$ 对 $1d$ 数据进行回归，该数据的噪声水平不断提高。$\textrm{(a)}$ 输出方差与输入有关，如图 $13.7$ 所示；$\textrm{(b)}$ 均值使用与 $\textrm{(a)}$ 一样的模型，但方差被当作是一个固定的参数 $\sigma^2$，该值使用 $\textrm{MLE}$ 估计，如 $11.2.3.6$ 所述。

13.2.4.4 MLP用于异方差回归

我们还可以使用 $\textrm{MLP}$ 实现回归任务。图 $\textrm{13.7}$ 展示了如何为异方差（$\textrm{heteroskedastic}$）非线性回归任务建模。（术语“异方差”仅表示预测的输出方差与输入有关，如第 $\textrm{3.3.3}$ 节中所述。）该函数具有两个输出，分别表示 $f_\mu(\mathbf{x})=\mathbb{E}[y|\mathbf{x},\mathbf{\theta}]$ 和 $f_\sigma(\mathbf{x})=\sqrt{\mathbb{V}[y|\mathbf{x},\mathbf{\theta}]}$。如图 $\textrm{13.7}$ 所示，通过使用一个共享的主干网络（$\textrm{backbone}$）和两个输出头网络（$\textrm{heads}$），我们可以在这两个函数之间共享大部分层（也包括其中的参数）。对于 $\mu$ 输出头，我们使用一个线性激活函数 $\varphi(a)=a$。对于 $\sigma$ 头，我们使用 $\textrm{softplus}$ 激活函数 $\varphi(a)=\sigma_{+}(a)$。如果我们使用线性输出头和一个非线性主干网络，整个模型定义为 $p(y|\mathbf{x},\mathbf{\theta})=\mathcal{N}(y|\mathbf{w}_\mathbf{\mu}^{\rm{T}}f(\mathbf{x};\mathbf{w}_{\rm{shared}}), \sigma_{+}(\mathbf{w}_{\mathbf{\sigma}}^{\rm{T}}f(\mathbf{x};\mathbf{w}_{\rm{shared}})))\tag{13.26}$ 图$\textrm{13.8}$ 显示了这种模型在某些数据集上的优势，在该数据集中，预测的期望值随时间线性增长，并且随季节波动，与此同时，数据的方差呈二次方增加趋势。（这是 随机波动率模型 （$\textrm{stochastic volatility model}$）的一个简单示例；它可以用于对财务数据以及地球的全球温度进行建模，其中地球温度的（由于气候变化）均值和方差不断增加。）我们发现将输出方差 $\sigma^2$ 视为固定（与输入无关）参数的回归模型置信度有时会比较低，因为模型需要适应整体的噪声水平，并且无法适应输入空间中每个点的噪声水平。

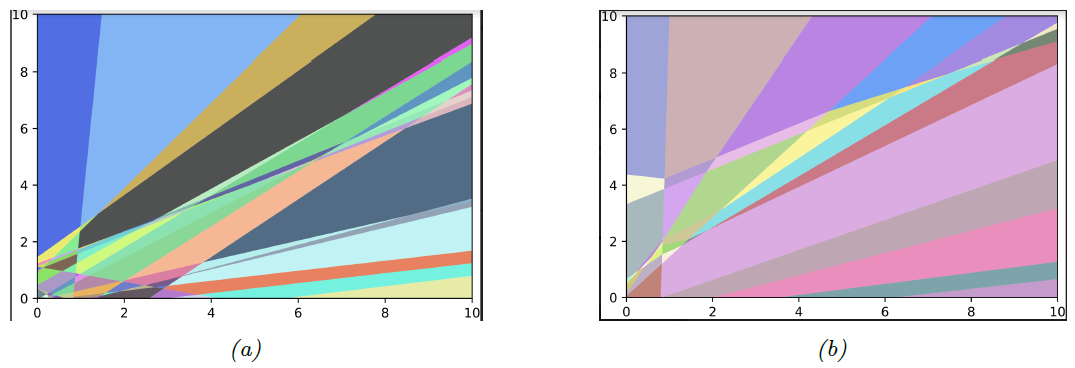
plane_decomposition

图 $\textrm{13.9}$：以 $ \textrm{ReLU} $ 为激活函数的 $\textrm{MLP}$ 将二维平面划分为有限个线性决策区域。$(a)$ 只有一个隐藏层，其中包含 $25$ 个节点； $(b)$ 含两个隐藏层。图形来源 [HAB19]¹².

13.2.5 网络深度的重要性

研究表明包含一个隐藏层的 $\textrm{MLP}$ 是一个通用函数逼近器（$\textrm{universal function approximator}$），这意味着只要给定足够的隐藏单元，$\textrm{MLP}$ 就可以逼近任何平滑函数，并能够达到任何所需的精度水平[HSW89]¹³; [cyb89]¹⁴; [Hor91]¹⁵。直观地讲，背后的原因在于每个隐藏层中的单元都可以指定一个超半平面，并且这些单元的足够大的组合可以“划分”空间的任何区域，我们可以将其与任何响应相关联（这在使用分段线性激活函数时最容易看到，如图 $13.9$ 所示。

但是，实验和理论上的各种观点（[Has87]¹⁶; [Mon+14]¹⁷; [Rag+17]¹⁸; [Pog+17]¹⁹）都表明，深层网络比浅层网络更有效。原因是更深的网络层可以利用浅层网络的所学习的特征。也就是说，该函数是以组合或分层的方式定义的。例如，假设我们要对 $\textrm{DNA}$ 字符串进行分类，并且正例与正则表达式 $\textbf{*AA??CGCG??AA* }$相关联。尽管我们可以使用含单个隐藏层的模型对数据进行拟合，但是从直观上来说，如果模型首先学会使用第 $\textrm{1}$ 层中的隐藏单元来检测 $\textrm{AA}$ 和 $\textrm{CG}$ “基元”（$\textrm{motifs}$），然后使用这些特征在第$2$层定义一个简单的线性分类器，类似于我们在$\textrm{13.2.1}$ 节中解决 $\textrm{XOR}$ 问题的思路。

13.2.5.1 深度学习革命

尽管 $\textrm{DNN}$ 背后的思想可以追溯到几十年前，但直到 $\textrm{2010}$ 年代，它们才开始被广泛使用。突破性的时刻发生在$\textrm{2012}$ 年，当时 [KSH12]⁶ 表明深层的 $\textrm{CNN}$ 可以在具有挑战性的 $\textrm{ImageNet}$ 图像分类数据集上显著提高性能，在一年内将错误率从$\textrm{26％}$降低到$\textrm{16％}$（见图 $\textrm{14.14b}$）；与之前每年约 $\textrm{2％}$ 的下降幅度相比，这是一个巨大的飞跃。大约在同一时间，[DHK13]²⁰ 表明，在各种语音识别任务上，深度神经网络可以大大优于现有技术。

$\textrm{DNN}$ 的“爆发”有几个促成因素。一是廉价的 $\textrm{GPU}$（图形处理单元）使用称为可能。它们最初是为了加快视频游戏的图像渲染速度而开发的，但是它们也可以大大减少大型 $\textrm{CNN}$ 的训练时间，其中包含相似的矩阵矢量计算。另一个是大规模含标签数据集的增长，这使得我们能够拟合包含大量参数的复杂函数，同时避免过拟合的风险。（例如，$\textrm{ImageNet}$ 具有$\textrm{130}$ 万张含标签的图像，可以用于拟合具有数百万个参数的模型）。的确，如果将深度学习系统视为“火箭”，那么大规模数据集就被称为燃料²¹。

由于 $\textrm{DNN}$ 在经验上取得了巨大的成功，许多公司开始对该技术产生兴趣，并开发了高质量的开源软件库，例如$\textrm{Tensorflow}$（由 $\textrm{Google}$ 开发），$\textrm{PyTorch}$（由 $\textrm{Facebook}$ 开发）和 $\textrm{MXNet}$（由亚马逊开发）。这些库支持复杂的微分函数的自动微分（请参考 $\textrm{13.3}$ 节）和可扩展的基于梯度的优化（请参见 $\textrm{5.4}$ 节）。在本书的不同地方，我们将使用其中的一些库来实现各种模型，而不仅仅是 $\textrm{DNN}$。

有关“深度学习革命”历史的更多详细信息，请参考[Sej18]²²。

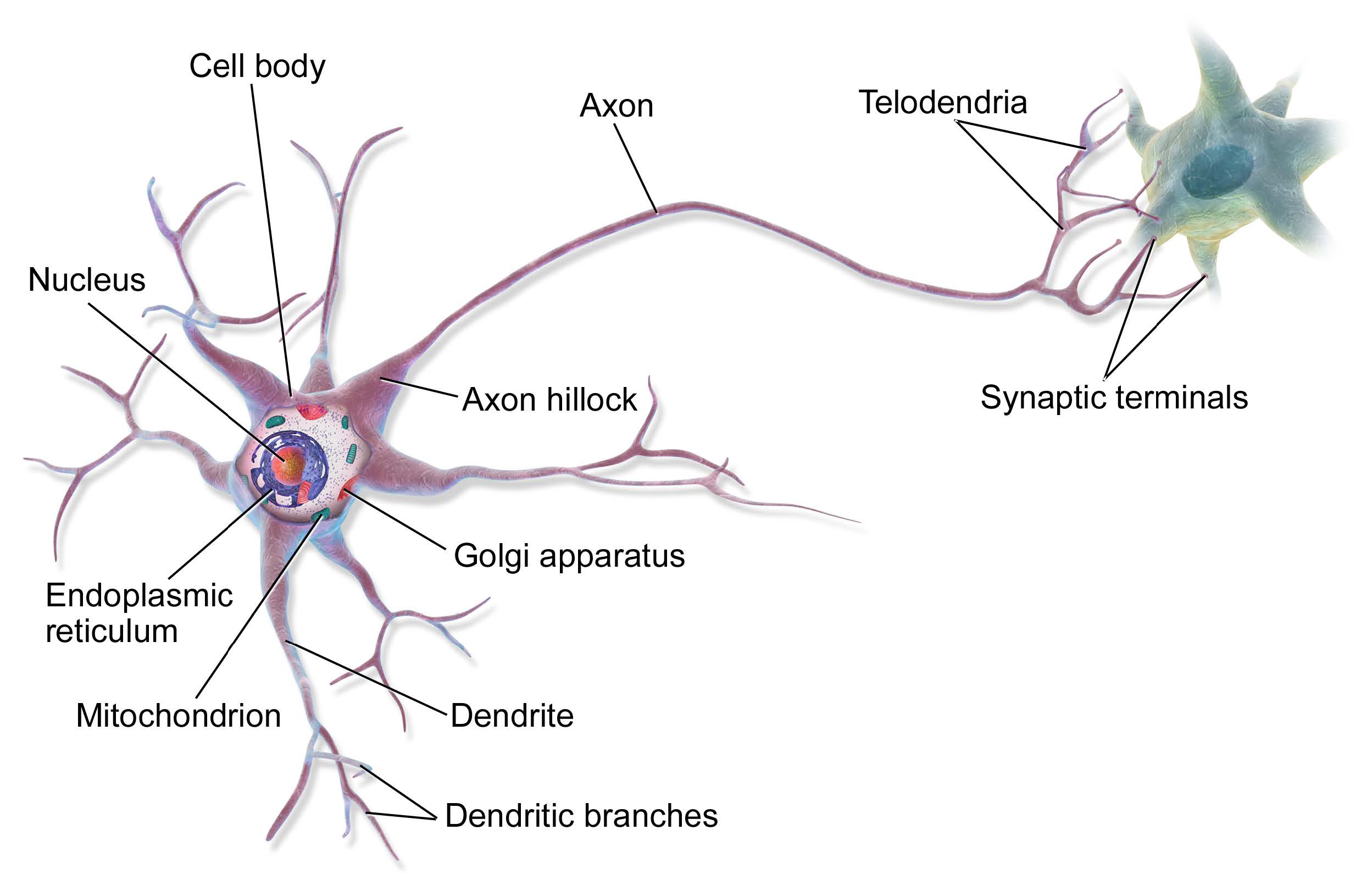
neurons

图 $13.10$: 在“电路”中连接在一起的两个神经元的图示。左侧神经元的输出轴突与右侧细胞的树突形成突触连接，电荷以离子流的形式存在，使细胞得以交流。来自 https://en.wikipedia.org/wiki/Neuron。在维基百科作者BruceBlaus的许可下使用。

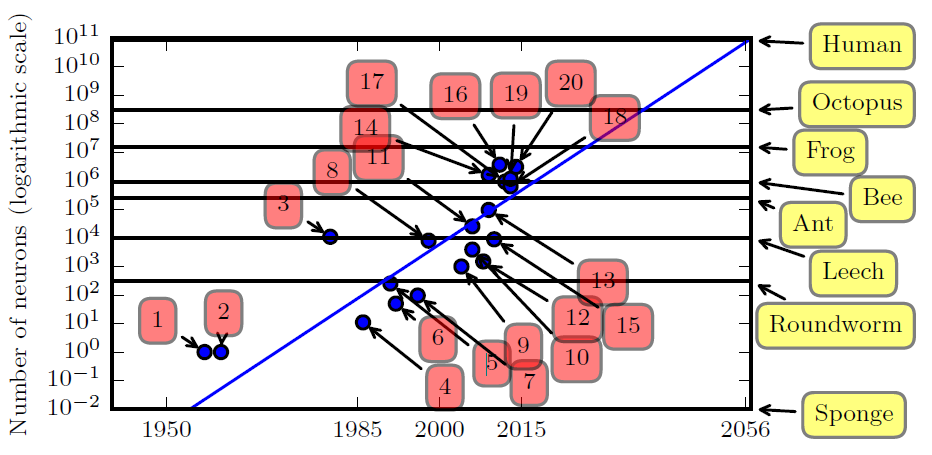
networkSize

图 $\textrm{13.11}$：神经网络大小随时间的变化趋势图。模型 $1,2,3$ 和 $4$ 表示感知机 [Ros58]²³，自适应线性单元（$\textrm{adaptive linear unit}$）[WH60][^WH60]，神经认知机（$\textrm{neocognitron}$）[Fuk80]²⁴ 和第一个利用反向传播算法训练的 $\textrm{MLP}$ [RHW86]²⁵。图形来自 [GBC16]²⁶的图 $1.11$。

13.2.6 与生物学的联系

在本节中，我们将讨论上文介绍的各种神经网络（称为人工神经网络, $\textrm{artificial neural networks, ANN}$）与实际神经网络之间的联系。真实的生物大脑工作细节非常复杂（参见 [Kan+12]²⁷），但是我们可以给出一个简单的“卡通”（$\textrm{cartoon}$）。

我们首先考虑单个神经元的模型。近似地讲，我们可以说神经元 $k$ 是否激活（用 $h_{k} \in{0,1}$ 表示）取决于其输入的行为（用 $\mathbf{x} \in \mathbb{R}^{D}$表示）以及连接的强度（用 $\mathbf{w} _k \in \mathbb{R}^D$表示）。我们可以使用 $a _{k}=\mathbf{w} _{k}^{\top} \mathbf{x}$ 来计算输入的加权和。这些权重可以看作是将输入 $x _d$ 连接到神经元 $h _k$ 的“电线”，类似于真实神经元中的树突（见图$\textrm{13.10} $）。该加权和接着被用于与阈值 $b _k $ 进行比较，如果激活超过阈值，则神经元触发；这类似于神经元发出电输出或动作电位。因此，我们可以使用 $h _{k}(\mathbf{x})=H\left(\mathbf{w} _k^\top \mathbf{x}-b _k\right) $ 来模拟神经元的行为，其中 $H(a)=\mathbb{I}(a>0)$ 是$\textrm{Heaviside}$函数。，这称为神经元的 $\textrm{McCulloch-Pitts}$ 模型，于 $\textrm{1943}$ 年提出 [MP43]²⁸。

我们可以将多个这样的神经元组合在一起以构成一个人工神经网络，最终的结果有时被视为大脑的模型。但是，人工神经网络在许多方面与生物大脑存在差异，主要包括以下方面：

大多数 $\textrm{ANN}$ 使用反向传播来修改其连接强度（请参见第 $\textrm{13.3}$ 节）。但是，真正的大脑不会使用反向传播，因为无法沿着轴突向后发送信息 [Ben+15b]²⁹; [BS16]³⁰;[KH19]³¹。相反，他们使用局部更新规则来调整突触强度。
大多数 $\textrm{ANN}$ 都是严格的前馈，但是真实的大脑有很多反馈连接。据信这种反馈的作用类似于先验，它们可以与来自感官系统的自下而上的似然结合起来，计算出已经包含经验信息的隐藏状态的后验，然后可以将其用于最佳决策（参考[Doy+07]³²）。
Most ANNs are strictly feedforward, but real brains have many feedback connections. It is believed that this feedback acts like a prior, which can be combined with bottom up likelihoods from the sensory system to compute a posterior over hidden states of the world, which can then be used for optimal decision making.
大多数人工神经网络使用简化的神经元，该神经元由处理线性组合的非线性单元组成，但实际的生物神经元具有复杂的树状结构（见图 $\textrm{13.10}$），具有复杂的时空动态。
大多数人工神经网络的大小和连接数均小于生物大脑（见图$\textrm{13.11}$）。当然，在各种新型硬件加速器（例如$\textrm{GPU}$ 和 $\textrm{TPU}$（张量处理单元）等）的推动下，人工神经网络每周都会变得越来越大。但是，即使人工神经网络在单元数量上与生物大脑相匹配，这种比较也具有误导性，因为生物神经元的处理能力远高于人工神经元（见上文）。
大多数 $\textrm{ANN}$ 被设计为对单个函数建模，例如将图像映射到类别标签，或将一个单词序列映射到另一个单词序列。相比之下，生物大脑是非常复杂的系统，由多个专门的交互模块组成，这些模块实现不同种类的功能或行为，例如感知，控制，记忆，语言等（请参见 [Sha88]³³; [Kan+12]²⁷）。

当然，我们正在努力建立逼真的生物大脑模型（例如，蓝脑计划, $\textrm{Blue Brain Project}$, [Mar06]³⁴; [Yon19]³⁵）。但是，一个有趣的问题是，以这种细致程度研究大脑是否对 “解决$\textrm{AI}$” 有用？通常认为，如果我们的目标是建造“智能机器”，那么生物大脑的浅层细节并不重要，就像飞机不会拍打自己的机翼一样。但是，“ $\textrm{AI}$”大概将遵循与智能生物代理类似的 “智能定律”（$\textrm{laws of intelligence}$），就像飞机和鸟类遵循相同的空气动力学定律一样。

不幸的是，我们尚不知道什么是“智能定律”，或者甚至是否存在这样的法则。在本书中，我们假设任何智能代理都应遵循信息处理和贝叶斯决策理论的基本原理，这是在不确定性下做出决策的最佳方法（请参见第 $\textrm{8.4.2}$ 节）。

当然，生物代理受到许多约束（例如，计算，生态），这通常需要算法“捷径”才能获得最佳解决方案。这可以解释人们在日常推理中使用的许多启发式方法。[KST82]³⁶; [GTA00]³⁷; [Gri20]³⁸。随着我们希望机器解决的任务变得越来越困难，我们也许能够从神经科学和认知科学的其他领域获得见识（例如，参见[MWK16]³⁹; [Has+17]⁴⁰; [Lak+17]⁴¹）。

Of course, there are efforts to make realistic models of biological brains (e.g., the Blue Brain Project [Mar06; Yon19]). However, an interesting question is whether studying the brain at this level of detail is useful for “solving AI”. It is commonly believed that the low level details of biological brains do not matter if our goal is to build “intelligent machines”, just as aeroplanes do not flap their wings. However, presumably “AIs” will follow similar “laws of intelligence” to intelligent biological agents, just as planes and birds follow the same laws of aerodynamics.
Unfortunately, we do not yet know what the “laws of intelligence” are, or indeed if there even are such laws. In this book we make the assumption that any intelligent agent should follow the basic principles of information processing and Bayesian decision theory, which is known to be the optimal way to make decisions under uncertainty (see Sec. 8.4.2).
Of course, biological agents are subject to many constraints (e.g., computational, ecological) which often require algorithmic “shortcuts” to the optimal solution; this can explain many of the heuristics that people use in everyday reasoning [KST82; GTA00; Gri20]. As the tasks we want our machines to solve become harder, we may be able to gain insights from other areas of neuroscience and cognitive science (see e.g., [MWK16; Has+17; Lak+17]).

13.3 反向传播

在本节，我们将介绍著名的 反向传播算法（$\textrm{backpropagation algorithm}$），正如第 $\textrm{13.4}$ 节讨论的，该算法可用于计算损失函数关于网络每一层参数的梯度，并将该梯度传递给基于梯度的优化算法。

反向传播算法最初由[BH69]⁴²提出，同时在[Wer74]⁴³中被独立发现。但是，该算法引起“主流”机器学习社区的注意，还要归功于[RHW86]²⁵。关于该算法的更多历史信息，请参考 $\textrm{Wikipedia page}$⁴⁴。

为了方便分析，我们首先假设计算图是一个简单的类似于 $\textrm{MLP}$ 的线性链，该线性链中的每一层都是一个线性映射函数。在这种情况下，反向传播等价于链式法则的重复使用（参考式（$\textrm{B.42}$））。但是，正如我们在第 $\textrm{13.3.4}$ 节中将要讨论的，该方法可以推广到任意的有向无环图（$\textrm{DAG}$）模型。整个反向传播算法的过程通常被称为 自动微分（$\textrm{automatic differentiation, autodiff}$）。

13.3.1 前向与反向模式微分

考虑一个形式为 $\mathbf{o}=\mathbf{f}(\mathbf{x})$ 的映射函数，其中 $\mathbf{x}\in \mathbb{R}^n$, $\mathbf{o}\in \mathbb{R}^m$。假设函数 $\mathbf{f}$ 由多个子函数组合而成： $\mathbf{f}=\mathbf{f}_4 \circ \mathbf{f}_3 \circ \mathbf{f}_2 \circ \mathbf{f}_1 \tag{13.27}$ 其中 $\mathbf{f}_1:\mathbb{R}^n \rightarrow \mathbb{R}^{m_1}$, $\mathbf{f}_2:\mathbb{R}^{m_1} \rightarrow \mathbb{R}^{m_2}$, $\mathbf{f}_3:\mathbb{R}^{m_2} \rightarrow \mathbb{R}^{m_3}$, $\mathbf{f}_4:\mathbb{R}^{m_3} \rightarrow \mathbb{R}^{m}$。为了得到最终的结果 $\mathbf{o}=\mathbf{f}(\mathbf{x})$, 需要依次计算中间过程 $\mathbf{x}_2=\mathbf{f}_1(\mathbf{x})$, $\mathbf{x}_3=\mathbf{f}_2(\mathbf{x}_2)$, $\mathbf{x}_4=\mathbf{f}_3(\mathbf{x}_3)$, $\mathbf{o}=\mathbf{f}_4(\mathbf{x}_4)$。

我们可以使用链式法则计算雅各比（$\textrm{Jacobian}$） $\mathbf{J}_\mathbf{f}(\mathbf{x})=\frac{\partial \mathbf{o}}{\partial \mathbf{x}}\in \mathbb{R}^{m\times n}$：

\[\begin{align} \frac{\partial \mathbf{o}}{\partial \mathbf{x}} = & \frac{\partial \mathbf{o}}{\partial \mathbf{x}_4}\frac{\partial \mathbf{x}_4}{\partial \mathbf{x}_3}\frac{\partial \mathbf{x}_3}{\partial \mathbf{x}_2}\frac{\partial \mathbf{x}_2}{\partial \mathbf{x}} = \frac{\partial \mathbf{f}_4(\mathbf{x}_4)}{\partial \mathbf{x}_4}\frac{\partial \mathbf{f}_3(\mathbf{x}_3)}{\partial \mathbf{x}_3}\frac{\partial \mathbf{f}_2(\mathbf{x}_2)}{\partial \mathbf{x}_2}\frac{\partial \mathbf{f}_1(\mathbf{x})}{\partial \mathbf{x}} \tag{13.28} \\ = & \mathbf{J}_{\mathbf{f}_4}(\mathbf{x}_4)\mathbf{J}_{\mathbf{f}_3}(\mathbf{x}_3)\mathbf{J}_{\mathbf{f}_2}(\mathbf{x}_2)\mathbf{J}_{\mathbf{f}_1}(\mathbf{x}_1) \tag{13.29} \end{align}\]

我们现在讨论如何高效地计算雅各比 $\mathbf{J}_\mathbf{f}(\mathbf{x})$。回顾雅各比的定义：

\[\mathbf{J}_\mathbf{f}(\mathbf{x}) = \frac{\partial \mathbf{f}(\mathbf{x})}{\partial \mathbf{x}}= \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{pmatrix} = \begin{pmatrix} \nabla f_1(\mathbf{x})^{\rm{T}} \\ \vdots \\ \nabla f_m(\mathbf{x})^{\rm{T}} \end{pmatrix} = \begin{pmatrix} \frac{\partial \mathbf{f}}{\partial x_1}, & \cdots, \frac{\partial \mathbf{f}}{\partial x_n} \end{pmatrix} \in \mathbb{R}^{m\times n} \tag{13.30}\]

其中 $\nabla f_i(\mathbf{x})^{\rm{T}} \in \mathbb{R} ^ {1 \times n}$ 为第 $i$ 行（ $i = 1:m$ ），$\frac{\partial \mathbf{f}}{\partial x_ j} \in \mathbb{R}^m$ 为第 $j$ 列（$j = 1:n$）。值得注意的是，当 $m = 1$ 时，梯度表示为 $\nabla \mathbf{f}(\mathbf{x})$ ，其形状与 $\mathbf{x}$ 相同，即是一个列向量，然而，此时 $\mathbf{J}_ {\mathbf{f}}(\mathbf{x})$ 是一个行向量，在这种情况下，我们令 $\nabla\mathbf{f}(\mathbf{x})=\mathbf{J} _{\mathbf{f}}(\mathbf{x})^{\top} $。

我们可以通过向量雅各比乘（$\textrm{vector Jacobian product，VJP}$）$\mathbf{e} _i^{\rm{T}}\mathbf{J} _\mathbf{f}(\mathbf{x})$ 从 $\mathbf{J} _\mathbf{f}(\mathbf{x})$ 中提取第 $i$ 行，其中 $\mathbf{e} _i \in \mathbb{R}^m$ 表示单位基向量。类似地，我们可以使用雅各比向量乘（$\textrm{Jacobian vector product, JVP}$）$\mathbf{J} _\mathbf{f}(\mathbf{x})\mathbf{e} _j$ 从 $\mathbf{J} _\mathbf{f}(\mathbf{x})$ 中提取第 $j$ 列，其中 $\mathbf{e} _j \in \mathbb{R}^n$。因此 $\mathbf{J} _\mathbf{f}(\mathbf{x})$ 的计算可以退化为 $\textrm{n}$ 个 $\textrm{JVPs}$ 或 $\textrm{m}$ 个 $\textrm{VJPs}$。[^译者注1]

如果 $n \lt m$，计算 $\mathbf{J}_\mathbf{f}(\mathbf{x})$ 的高效方法是，对每一列 $j=1:n$ 使用 $\textrm{JVPs}$，并在计算的过程中使用从右到左的计算顺序。右乘列向量的形式为：

\[\mathbf{J}_{\mathbf{f}}(\mathbf{x}) \mathbf{v}=\underbrace{\mathbf{J}_{\mathbf{f}_{4}}\left(\mathbf{x}_{4}\right)}_{m \times m_{3}} \underbrace{\mathbf{J}_{\mathrm{f}_{3}}\left(\mathbf{x}_{3}\right)}_{m_{3} \times m_{2}} \underbrace{\mathbf{J}_{\mathrm{f}_{2}}\left(\mathbf{x}_{2}\right)}_{m_{2} \times m_{1}} \underbrace{\mathbf{J}_{\mathbf{f}_{1}}\left(\mathbf{x}_{1}\right)}_{m_{1} \times n} \underbrace{\mathbf{v}}_{n \times 1} \tag{13.31}\]

上式可以通过前向模式微分（$\textrm{forward mode differentiation}$）得到；算法 $\textrm{5}$ 给出了伪代码。假设 $m=1$，同时 $n=m_1=m_2=m_3$，计算 $\mathbf{J}_\mathbf{f}(\mathbf{x})$ 的时间复杂度为 $O(n^3)$。

$\textrm{Algorithm 5}$: 前向模式微分
$\mathbf{x}_{1}:=\mathbf{x}$
$\mathbf{v}_j:=\mathbf{e}_j \in \mathbb{R}^n$ $\textrm{for}$ $j=1: n$
$\textbf{for}$ $k=1:K$ $\textbf{do}$
$\mathbf{x}_{k+1}=\mathbf{f}_k\left(\mathbf{x}_k\right)$
$\mathbf{v} _j:=\mathbf{J} _{\mathbf{f}_k}(\mathbf{x} _k)\mathbf{v} _j \textrm{ for }j=1: n$
$\textrm{Return}$ $\mathbf{o}=\mathbf{x} _{K+1},\left[\mathbf{J} _{\mathbf{f}}(\mathbf{x})\right] _{:, j}=\mathbf{v} _j\textrm{ for }j=1: n$

如果 $n \gt m$ （比如说，输出是一个标量），高效的计算方式是，对每一行 $i = 1 : m$ 使用 $\textrm{VJPs}$，并采用从左到右的计算方式。左乘行向量 $\mathbf{u}^{\rm{T}}$ 的形式为 $\mathbf{u}^{\top} \mathbf{J}_{\mathbf{f}}(\mathbf{x})=\underbrace{\mathbf{u}^{\top}}_{1 \times m} \underbrace{\mathbf{J}_{\mathrm{f}_{4}}\left(\mathbf{x}_{4}\right)}_{m \times m_{3}} \underbrace{\mathbf{J}_{\mathbf{f}_{3}}\left(\mathbf{x}_{3}\right)}_{m_{3} \times m_{2}} \underbrace{\mathbf{J}_{\mathbf{f}_{2}}\left(\mathbf{x}_{2}\right)}_{m_{2} \times m_{1}} \underbrace{\mathbf{J}_{\mathbf{f}_{1}}\left(\mathbf{x}_{1}\right)}_{m_{1} \times n} \tag{13.32}$ 上式可以通过使用反向模式微分 （$\textrm{reverse mode differentiation}$）。算法 $6$ 给出了伪代码。假设 $m = 1$，同时 $n = m_1=m_2=m_3$，其计算复杂度为 $O(n^2)$。

$\textrm{Algorithm 6}$: 反向模式微分
$\mathbf{x}_{1}:=\mathbf{x}$
$\textbf{for}$ $k=1:K$ $\textbf{do}$
$\mathbf{x} _{k+1}=\mathbf{f} _{k}\left(\mathbf{x} _{k}\right)$
$\mathbf{u} _{i}:=\mathbf{e} _{i} \in \mathbb{R}^{m}$ $\textrm{for}$ $i=1: m$
$\textbf{for}$ $k=K:1$ $\textbf{do}$
$\mathbf{u} _{i}^{\top}:=\mathbf{u} _{i}^{\top} \mathbf{J} _{\mathbf{f} _{k}}\left(\mathbf{x} _{k}\right)$ $\textbf{for}$ $i=1: m$
$\textrm{Return}$ $\mathbf{o}=\mathbf{x} _{K+1},\left[\mathbf{J} _{\mathbf{f}}(\mathbf{x})\right] _{i,:}=\mathbf{u} _{i}^{\top}$ $\textrm{for}$ $i=1: m$

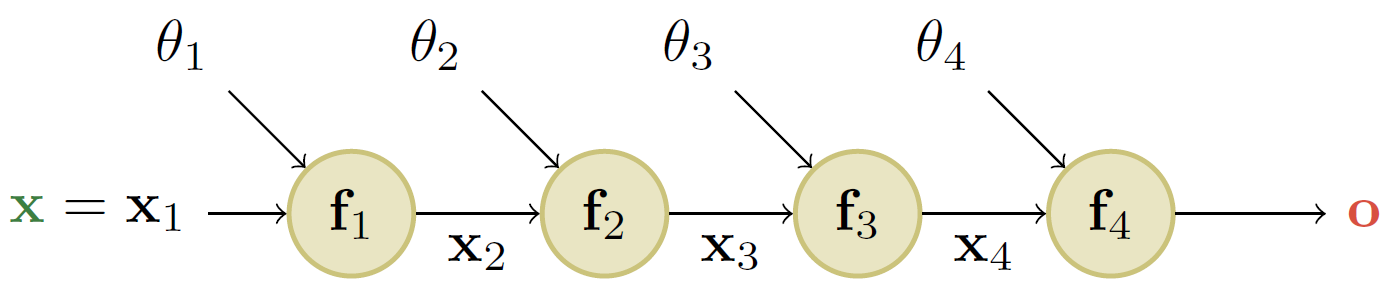
feedforward_model_with_4_layers

图 $13.12$: 一个简单的包含 $4$ 层的线性链式前馈网络。其中 $\mathbf{x}$ 表示输入， $\mathbf{o}$ 表示输出。

13.3.2 用于多层感知机的反向模式微分

在之前的章节中，我们仅仅考虑了一个简单的线性链式前馈网络，其中的每一层都不包含可学习的参数。本节，所考虑的网络中每一层包含参数 $\mathbf{\theta}_1,…,\mathbf{\theta}_4$，如图 $13.12$ 所示。我们集中讨论最终输出为标量的情况：$\mathcal{L}:\mathbb{R}^n\rightarrow \mathbb{R}$。举例来说，考虑作用于包含一个隐藏层的 $\textrm{MLP}$ 的 $l_2$ 损失函数： $\mathcal{L}((\mathbf{x}, \mathbf{y}), \boldsymbol{\theta})=\frac{1}{2}\left\|\mathbf{y}-\mathbf{W}_{2} \varphi\left(\mathbf{W}_{1} \mathbf{x}\right)\right\|_{2}^{2} \tag{13.33}$ 我们可以将上式表示为如下的前馈网络模型： $\begin{align} \mathcal{L} &=\mathbf{f}_{4} \circ \mathbf{f}_{3} \circ \mathbf{f}_{2} \circ \mathbf{f}_{1} \tag{13.34} \\ \mathbf{x}_{2} &=\mathbf{f}_{1}\left(\mathbf{x}, \boldsymbol{\theta}_{1}\right)=\mathbf{W}_{1} \mathbf{x} \tag{13.35} \\ \mathbf{x}_{3} &=\mathbf{f}_{2}\left(\mathbf{x}_{2}, \emptyset\right)=\varphi\left(\mathbf{x}_{2}\right) \tag{13.36} \\ \mathbf{x}_{4} &=\mathbf{f}_{3}\left(\mathbf{x}_{3}, \boldsymbol{\theta}_{3}\right)=\mathbf{W}_{2} \mathbf{x}_{3} \tag{13.37} \\ \mathcal{L} &=\mathbf{f}_{4}\left(\mathbf{x}_{4}, \mathbf{y}\right)=\frac{1}{2}\left\|\mathbf{x}_{4}-\mathbf{y}\right\|^{2} \tag{13.38} \end{align}$ 我们用符号 $\mathbf{f}_k(\mathbf{x}_k,\boldsymbol{\theta}_k)$ 表示第 $k$ 层的函数，其中 $\mathbf{x}_k$ 为上一层的输出， $\boldsymbol{\theta}_k$ 表示该层的可选参数。

在这个例子中，最后一层的输出为一个标量，因为它对应于一个损失函数 $\mathcal{L}\in \mathbb{R}$。所以使用反向模式微分计算梯度向量的效率更高。

我们首先讨论如何计算标量输出关于每一层中参数的梯度。我们可以使用矢量微积分直接计算 $\frac{\partial L}{\partial \boldsymbol{\theta} _{4}}$。对于中间项，我们使用链式法则：

\[\begin{align} \frac{\partial \mathcal{L}}{\partial \boldsymbol{\theta}_{3}}&=\frac{\partial \mathcal{L}}{\partial \mathbf{x}_{4}} \frac{\partial \mathbf{x}_{4}}{\partial \boldsymbol{\theta}_{3}} \tag{13.39}\\ \frac{\partial \mathcal{L}}{\partial \boldsymbol{\theta}_{2}}&=\frac{\partial \mathcal{L}}{\partial \mathbf{x}_{4}} \frac{\partial \mathbf{x}_{4}}{\partial \mathbf{x}_{3}} \frac{\partial \mathbf{x}_{3}}{\partial \boldsymbol{\theta}_{2}} \tag{13.40} \\ \frac{\partial \mathcal{L}}{\partial \boldsymbol{\theta}_{1}}&=\frac{\partial \mathcal{L}}{\partial \mathbf{x}_{4}} \frac{\partial \mathbf{x}_{4}}{\partial \mathbf{x}_{3}} \frac{\partial \mathbf{x}_{3}}{\partial \mathbf{x}_{2}} \frac{\partial \mathbf{x}_{2}}{\partial \boldsymbol{\theta}_{1}} \tag{13.41} \end{align}\]

其中 $\frac{\partial \mathcal{L}}{\partial \boldsymbol{\theta}_ {k}}=\left(\nabla_ {\boldsymbol{\theta}_ {k}} \mathcal{L}\right)^{\top}$ 是一个 $d _k$ 维的行向量，$d _k$ 为第 $k$ 层的参数数量。我们发现这些值可以通过递归方式进行计算，即将第 $k$ 层的梯度行向量与大小为 $n _{k} \times n _{k-1}$ 的雅各比 $\frac{\partial \mathbf{x} _{k}}{\partial \mathbf{x} _{k-1}}$ 相乘，其中 $n _k$ 为第 $k$ 层隐藏节点的数量。算法 $7$ 给出了伪代码。

$\textrm{Algorithm 7}$: 含 $K$ 层的 $\textrm{MLP}$ 的反向传播算法
$\textrm{// Forward pass}$
$\mathbf{x}_{1}:=\mathbf{x}$
$\textbf{for}$ $k=1:K$ $\textbf{do}$
$\mathbf{x} _{k+1}=\mathbf{f} _{k}\left(\mathbf{x} _{k}, \pmb{\theta} _k\right)$
$\textrm{// Backward pass}$
$\mathbf{u}_{K+1} := \mathbf{1}$
$\textbf{for}$ $k=K:1$ $\textbf{do}$
$\mathbf{g} _{k}:=\mathbf{u} _{k+1}^{\top} \frac{\partial \mathbf{f} _{k}\left(\mathbf{x} _{k}, \boldsymbol{\theta} _{k}\right)}{\partial \boldsymbol{\theta} _{k}}$
$\mathbf{u} _{k}^{\top}:=\mathbf{u} _{k+1}^{\top} \frac{\partial \mathbf{f} _{k}\left(\mathbf{x} _{k}, \boldsymbol{\theta} _{k}\right)}{\partial \mathbf{x} _{k}}$
$\textrm{// Output}$
$\textrm{Return}$ $\mathcal{L}=\mathrm{x} _{K+1}$, $\nabla _{\mathbf{x}} \mathcal{L}=\mathbf{u} _{1}$, $\left\{\nabla _{\boldsymbol{\theta} _{k}} \mathcal{L}=\mathrm{g} _{k}: k=1: K\right\}$

该算法计算出损失关于每一层参数的梯度。同时还计算了损失关于输入的梯度 $\nabla_{\mathbf{x}} \mathcal{L} \in \mathbb{R}^{n}$ ，其中 $n$ 表述输入的维度。后一项对于参数的更新并不需要，但对于需要生成输入 $\mathbf{x}$ 的模型来说却是有用的（见 $ 14.5$ 节）。

剩下的部分就是如何计算具体层的向量雅各比乘（$\textrm{VJP}$）。其中的细节取决于每一层映射函数的具体形式。我们在下文讨论一些具体的例子。

13.3.3 常规层的向量雅各比乘

回顾形式为 $\mathbf{f}:\mathbb{R}^n\rightarrow \mathbb{R}^m$ 的网络层的雅各比矩阵：

\[\mathbf{J}_{\mathbf{f}}(\mathbf{x})=\frac{\partial \mathbf{f}(\mathbf{x})}{\partial \mathbf{x}}=\left(\begin{array}{ccc} \frac{\partial f_{1}}{\partial x_{1}} & \cdots & \frac{\partial f_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & \cdots & \frac{\partial f_{m}}{\partial x_{n}} \end{array}\right)=\left(\begin{array}{c} \nabla f_{1}(\mathbf{x})^{\top} \\ \vdots \\ \nabla f_{m}(\mathbf{x})^{\top} \end{array}\right)=\left(\frac{\partial \mathbf{f}}{\partial x_{1}}, \cdots, \frac{\partial \mathbf{f}}{\partial x_{n}}\right) \in \mathbb{R}^{m \times n} \tag{13.42}\]

其中 $\nabla f_{i}(\mathbf{x})^{\top} \in \mathbb{R}^{n}$ 表示第 $i$ 行（$i = 1:m$），$\frac{\partial \mathbf{f}}{\partial x_{j}} \in \mathbb{R}^{m}$ 为第 $j$ 列（$j=1:n$）。本节，我们将描述如何计算常规层的 $\textrm{VJP}$ $\mathbf{u}^{\top} \mathbf{J}_{\mathbf{f}}(\mathbf{x})$ 。

13.3.3.1 交叉熵层

考虑一个交叉熵损失层，其输入为 $\textrm{logits}$ $\mathbf{x}$ 和真实标签 $\mathbf{y}$，损失层返回一个标量： $z=f(\mathbf{x})=\text { CrossEntropyWithLogits }(\mathbf{y}, \mathbf{x})=-\sum_{c} y_{c} \log p_{c} \tag{13.43}$ 其中 $\mathbf{p}=\mathcal{S}(\mathbf{x})=\frac{e^{x_{c}}}{\sum_{c^{\prime}=1}^{C} e^{x_{c^{\prime}}}}$ 表示预测的类别概率值， $\mathbf{y}$ 为标签的 $\textrm{one-hot}$ 编码。（所以 $\mathbf{p}$ 和 $\mathbf{y}$ 都是维度为 $C$ 的概率单纯形（$\textrm{simplex}$）。）输出关于输入的雅各比为： $\mathbf{J}=\frac{\partial z}{\partial \mathbf{x}}=(\mathbf{p}-\mathbf{y})^{\top} \in \mathbb{R}^{1 \times C} \tag{13.44}$ 为了说明这一点，假设目标的真实类别为 $c$。我们有 $z=f(\mathbf{x})=-\log \left(p_{c}\right)=-\log \left(\frac{e^{x_{c}}}{\sum_{j} e^{x_{j}}}\right)=\log \left(\sum_{j} e^{x_{j}}\right)-x_{c} \tag{13.45}$ 所以 $\frac{\partial z}{\partial x_{i}}=\frac{\partial}{\partial x_{i}} \log \sum_{j} e^{x_{j}}-\frac{\partial}{\partial x_{i}} x_{c}=\frac{e^{x_{i}}}{\sum_{j} e^{x_{j}}}-\frac{\partial}{\partial x_{i}} x_{c}=p_{i}-\mathbb{I}(i=c) \tag{13.46}$ 定义 $\mathbf{y}=[\mathbb{I}(i=c)]$ ，我们将获得式 ($13.44$)。需要注意的是该层的雅各比是一个行向量，因为输出是一个标量。对应的 $\textrm{VJP}$ 为 $\mathbf{u}^{\top} \mathbf{J}$ ，其中 $\mathbf{u} \in \mathbb{R}$ 。

13.3.3.2 逐元素非线性

考虑使用逐元素非线性的网络层 $\mathbf{z}=\mathbf{f}(\mathbf{x})=\varphi(\mathbf{x})$ ，所以 $z_{i}=\varphi\left(x_{i}\right)$ 。雅各比的 $(i,j)$ 元素值为： $\frac{\partial z_{i}}{\partial x_{j}}=\left\{\begin{array}{ll} \varphi^{\prime}\left(x_{i}\right) & \text { if } i=j \\ 0 & \text { otherwise } \end{array}\right. \tag{13.47}$ 其中 $\varphi^{\prime}(a)=\frac{d}{d a} \varphi(a)$。换句话说，输出关于输入的雅各比为 $\mathbf{J}=\frac{\partial \mathbf{f}}{\partial \mathbf{x}}=\operatorname{diag}\left(\varphi^{\prime}(\mathbf{x})\right) \tag{13.48}$ 对于任意一个向量 $\mathbf{u}$，我们可以将 $\mathbf{J}$ 的对角元素与向量 $\mathbf{u}$ 进行逐元素相乘，得到 $\mathbf{u}^{\top} \mathbf{J}$。举例来说，假设 $\varphi(a)=\operatorname{ReLU}(a)=\max (a, 0) \tag{13.49}$ 我们有 $\varphi^{\prime}(a)=\left\{\begin{array}{ll} 0 & a<0 \\ 1 & a>0 \end{array}\right. \tag{13.50}$ 其中 $a=0$ 处的亚梯度（$\textrm{subderivative}$）（见 $\textrm{B.4.4}$）为 $[0,1]$ 区间的任意值。通常情况下等于 $0$。所以 $\operatorname{ReLU}^{\prime}(a)=H(a) \tag{13.51}$ 其中 $H$ 为单位阶跃函数。

13.3.3.3 线性层

现在考虑线性层，$\mathbf{z}=\mathbf{f}(\mathbf{x}, \mathbf{W})=\mathbf{W} \mathbf{x}$ ，其中 $\mathbf{W} \in \mathbb{R}^{m \times n}$ , 所以 $\mathbf{x} \in \mathbb{R}^{n}$ ，$\mathbf{z} \in \mathbb{R}^{m}$。我们可以计算关于输入向量的雅各比， $\mathbf{J}=\frac{\partial \mathbf{z}}{\partial \mathbf{x}} \in \mathbb{R}^{m \times n}$ 。注意到 $z_{i}=\sum_{k=1}^{n} W_{i k} x_{k} \tag{13.52}$ 所以雅各比的 $(i,j)$ 项为 $\frac{\partial z_{i}}{\partial x_{j}}=\frac{\partial}{\partial x_{j}} \sum_{k=1}^{n} W_{i k} x_{k}=\sum_{k=1}^{n} W_{i k} \frac{\partial}{\partial x_{j}} x_{k}=W_{i j} \tag{13.53}$ 因为 $\frac{\partial}{\partial x_{j}} x_{k}=\mathbb{I}(k=j)$ 。所以关于输入的雅各比为 $\mathbf{J}=\frac{\partial \mathbf{z}}{\partial \mathbf{x}}=\mathbf{W} \tag{13.54}$ $\mathbf{u}^{\top} \in \mathbb{R}^{1 \times m}$ 与 $\mathbf{J} \in \mathbb{R}^{m \times n}$ 的 $\textrm{VJP}$ 为 $\mathbf{u}^{\top} \frac{\partial \mathbf{z}}{\partial \mathbf{x}}=\mathbf{u}^{\top} \mathbf{W} \in \mathbb{R}^{1 \times n} \tag{13.55}$ 我们现在考虑关于权重矩阵的雅各比 $J=\frac{\partial \mathbf{z}}{\partial \mathbf{W}}$ 。它可以表示为一个 $m\times(m\times n)$的矩阵，处理起来会比较麻烦。所以取而代之的，我们关注对单个权重 $W_{ij}$ 的梯度。这个就比较容易计算了，因为 $\frac{\partial \mathbf{z}}{\partial W_{i j}}$ 是一个向量。为了计算该值，注意到 $\begin{align} z_{k} &=\sum_{l=1}^{m} W_{k l} x_{l} \tag{13.56} \\ \frac{\partial z_{k}}{\partial W_{i j}} &=\sum_{l=1}^{m} x_{l} \frac{\partial}{\partial W_{i j}} W_{k l}=\sum_{l=1}^{m} x_{l} \mathbb{I}(i=k \text { and } j=l) \tag{13.57} \end{align}$ 所以 $\frac{\partial \mathbf{z}}{\partial W_{i j}}=\left(\begin{array}{lllllll} 0 & \cdots & 0 & x_{j} & 0 & \cdots & 0 \end{array}\right)^{\top} \tag{13.58}$ 其中非零项处在位置 $i$。$\mathbf{u}^{\top} \in \mathbb{R}^{1 \times m}$ 与 $\frac{\partial \mathbf{z}}{\partial \mathbf{W}} \in \mathbb{R}^{m \times(m \times n)}$ 之间的 $\textrm{VJP}$ 可以表示为一个形状为 $1 \times(m \times n)$ 的矩阵。需要注意的是 $\mathbf{u}^{\top} \frac{\partial \mathbf{z}}{\partial W_{i j}}=\sum_{k=1}^{m} u_{k} \frac{\partial z_{k}}{\partial W_{i j}}=u_{i} x_{j} \tag{13.59}$ 所以 $\left[\mathbf{u}^{\top} \frac{\partial \mathbf{z}}{\partial \mathbf{W}}\right]_{1,:}=\mathbf{u x}^{\top} \in \mathbb{R}^{m \times n} \tag{13.60}$

13.3.3.4 将它们放在一起

练习 $13.1$ 需要将它们放在一起。

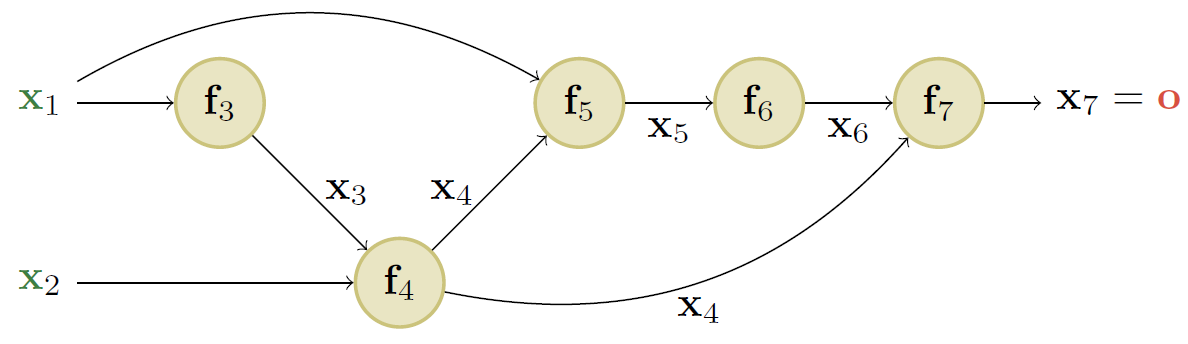
computation_graph

图 $13.13$: 包含 $2$ 个（标量）输入和 $1$ 个（标量）输出的计算图。

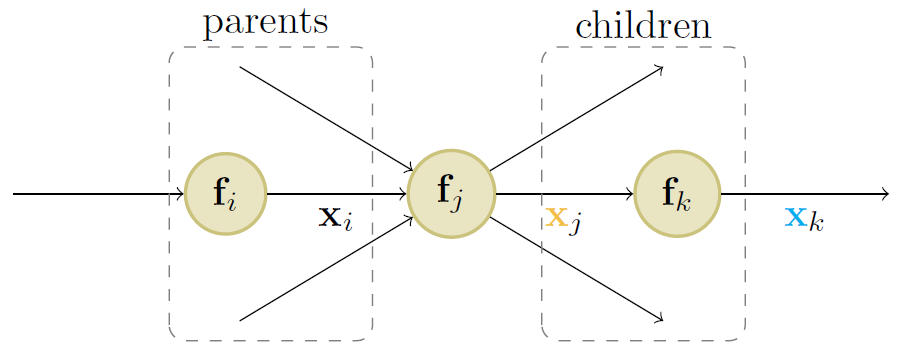
auto_diff

图 $13.14$：计算图中节点 $j$ 的自动微分的图示。

13.3.4 计算图

$\textrm{MLPs}$ 是一种简单的 $\textrm{DNN}$ 模型，其中每一层的输出直接输入到下一层，从而形成一个链式结构，如图 $13.12$ 所示。然而，最新的 $\textrm{DNN}$ 模型可以以更加复杂的形式组合可微的部件，从而构成一个 计算图（$\textrm{computation graph}$），这一点类似于程序员将初等函数组合成更加复杂的函数。（的确，有些人也建议将 “深度学习” 称为 “可微编程”（$\textrm{differentiable programming}$））唯一的约束在于最终的计算图对应于一个有向无环图（$\textrm{directed ayclic graph, DAG}$），其中每一个节点都是关于输入的可微函数。

举个例子，考虑函数 $f\left(x_{1}, x_{2}\right)=x_{2} e^{x_{1}} \sqrt{x_{1}+x_{2} e^{x_{1}}} \tag{13.61}$ 我们可以使用图 $13.13$ 中的 $\textrm{DAG}$ 进行计算，其中包含如下的中间函数： $\begin{align}{l} x_{3}& =f_{3}\left(x_{1}\right)=e^{x_{1}} \tag{13.62} \\ x_{4}& =f_{4}\left(x_{2}, x_{3}\right)=x_{2} x_{3} \tag{13.63} \\ x_{5}& =f_{5}\left(x_{1}, x_{4}\right)=x_{1}+x_{4} \tag{13.64}\\ x_{6}& =f_{6}\left(x_{5}\right)=\sqrt{x_{5}} \tag{13.65} \\ x_{7}& =f_{7}\left(x_{4}, x_{6}\right)=x_{4} x_{6} \tag{13.66} \end{align}$ 值得注意的是我们已经按照拓扑结构对节点进行了编号（父节点在子节点之前）。在反向传播期间，因为计算图不再是链式结构，我们需要对多条路径的梯度进行求和。举例来说，因为 $x_4$ 影响 $x_5$ 和 $x_7$，我们有 $\frac{\partial \mathrm{o}}{\partial \mathrm{x}_{4}}=\frac{\partial \mathrm{o}}{\partial \mathrm{x}_{5}} \frac{\partial \mathrm{x}_{5}}{\partial \mathrm{x}_{4}}+\frac{\partial \mathrm{o}}{\partial \mathrm{x}_{7}} \frac{\partial \mathrm{x}_{7}}{\partial \mathrm{x}_{4}} \tag{13.67}$ 通过逆拓扑顺序的计算方式，我们可以避免重复计算 $\begin{align} \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{7}}= & \frac{\partial \mathbf{x}_{7}}{\partial \mathbf{x}_{7}}=\mathbf{I}_{m} \tag{13.68} \\ \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{6}}= & \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{7}} \frac{\partial \mathbf{x}_{7}}{\partial \mathbf{x}_{6}} \tag{13.69}\\ \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{5}}= & \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{6}} \frac{\partial \mathbf{x}_{6}}{\partial \mathbf{x}_{5}} \tag{13.70} \\ \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{4}}= & \frac{\partial \mathbf{o}}{\partial \mathbf{x}_{5}} \frac{\partial \mathbf{x}_{5}}{\partial \mathbf{x}_{4}}+\frac{\partial \mathbf{o}}{\partial \mathbf{x}_{7}} \frac{\partial \mathbf{x}_{7}}{\partial \mathbf{x}_{4}} \tag{13.71} \end{align}$ 总而言之，我们使用 $\frac{\partial \mathrm{o}}{\partial \mathrm{x}_{j}}=\sum_{k \in \text { children }(j)} \frac{\partial \mathrm{o}}{\partial \mathrm{x}_{k}} \frac{\partial \mathrm{x}_{k}}{\partial \mathrm{x}_{j}} \tag{13.72}$ 其中我们对节点 $j$ 的所有子节点 $k$ 进行求和，如图 $13.14$ 所示。对于每个子节点 $k$ 的梯度向量 $\frac{\partial \mathbf{o}}{\partial \mathbf{x}{k}}$ 已经被计算，并被称为共轭矩阵（$\textrm{adjoint}$），该值用于与每个子节点的雅各比 $\frac{\partial \mathbf{x}{k}}{\partial \mathbf{x}_{j}}$ 相乘。

通过使用 $\textrm{API}$ 的定义静态图，可以提前计算出计算图（ $\textrm{Tensorflow 1}$ 的工作原理。）或者，可以通过跟踪函数在输入上的执行情况来“及时”计算计算图（这就是 $\textrm{Tensorflow-eager}$ 模式以及 $\textrm{JAX}$ 和 $\textrm{PyTorch}$ 的工作原理。）后一种方法使处理动态图变得更容易，动态图的形状可以根据函数计算的值而改变。

13.4 训练神经网络

本节，我们将讨论如何基于数据对 $\textrm{DNNs}$ 进行训练。最标准的方式是使用最大似然估计，通过最小化负对数似然： $\mathcal{L}(\theta)=-\log p(\mathcal{D} \mid \theta)=-\sum_{n=1}^{N} \log p\left(\mathbf{y}_{n} \mid \mathbf{x}_{n} ; \theta\right) \tag{13.73}$ 通常情况下，也会增加一个正则项（比如负对数先验），正如我们在 $13.5$ 节讨论的那样。

原则上，我们可以使用 $\textrm{backprop}$ 算法（第 $13.3$ 节）来计算这种损失的梯度，并将其传递给在第 $5$ 章中所讨论的现成的优化器。（第 $5.4.6.3$ 节中的 $\textrm{Adam}$ 优化器是一个普遍的选择，因为它能够扩展到大型数据集（由于是 $\textrm{SGD}$ 类型的算法），并且能够相当快速地收敛（由于使用对角预处理和动量）。）但是，在实践中，也有可能无法取得较好的结果。在本节中，我们将讨论可能出现的各种问题，以及一些解决方案。有关 $\textrm{DNN}$ 训练策略的更多详细信息，请参阅其他书籍[HG20]¹；[Zha+19a]²；[Ger19]³。

除了具体的实践问题，还有重要的理论问题。特别地，我们注意到 $\textrm{DNN}$ 损失不是一个凸目标，所以通常我们无法找到全局最优解。尽管如此，$\textrm{SGD}$ 总能收敛到出人意料的好的结果。具体的原因仍在研究当中，可以参考[Bah+20]⁴⁵对一些最近工作的回顾。

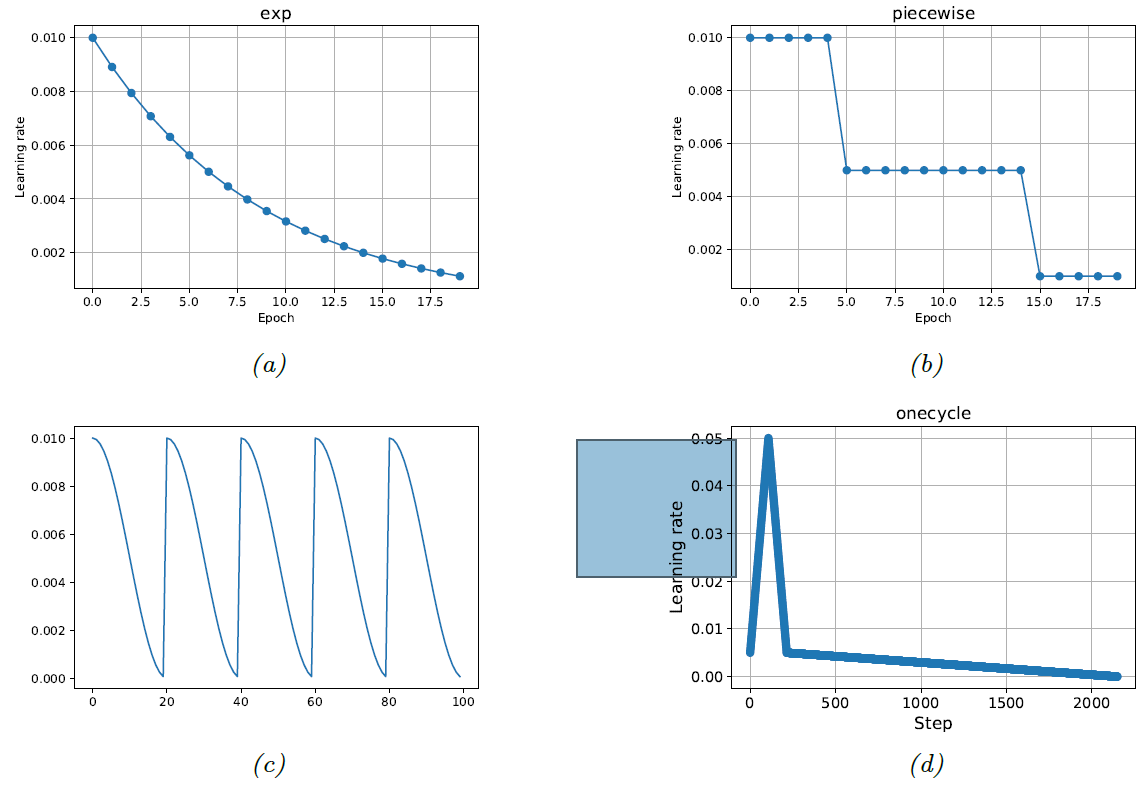
lr_sche

图$13.15$: 不同的学习率启发方式。$(a)$ 指数下降方案；$(b)$ 分段常数方案；$(c)$ 余弦退火方案（又被称为 含重启器的随机梯度（$\textrm{stochastic gradient with restarts}$））[Smi17]⁴⁶,[LH17]⁴⁷；$(d)$ 单周期方案[Smi18]⁴⁸。

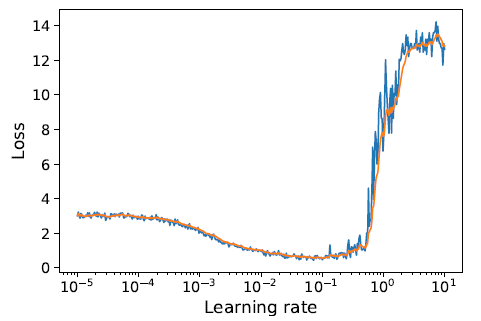
lr_finder

图$13.16$: 训练损失与学习率的关系，在 $FashionMNIST$ 数据集上，使用原生的 $SGD$ 拟合一个小的 $MLP$ 模型。（蓝色为原始损失，橘黄色为 $EWMA$ 版本）。

13.4.1 调整学习率

在用 $\textrm{SGD}$ 训练 $\textrm{DNN}$ 时，调整学习速率对于取得良好的性能非常重要。在第 $5.4.3$ 节中，我们讨论了 $\textrm{SGD}$ 的学习率若要收敛到局部最优值必须满足的必要条件，但是这些条件并没有精确地指出要使用什么样的学习率调节方案（$\textrm{learning rate schedule}$）。

在深度学习文献中，提出了许多启发式的方案，其中一些方法如图 $13.15$ 所示。包括分段常数策略（图$\textrm{13.15b}$）、余弦或周期策略（图$\textrm{13.15c}$）、单周期策略（图$\textrm{13.15d}$）等（后者首先从一个较小的学习率开始，以防止参数“爆炸”，然后逐步增加，直到找到一个比较好的学习率，接着再逐步下降，以找到局部最小值）

除了选择学习率的衰减策略外，还需要选择初始学习率 $\eta_{0}$。[BCN18]⁴⁹提出了一种常见的启发式方法，该方法在[Smi18]⁴⁸中被同时发现（并称之为“学习速率发现器”（$\textrm{learning rate finder}$）），该方法定义为：从一个较小的学习率开始，计算小批量数据的训练或验证损失，然后依次尝试更大的（每一步增加 $10$ 倍）学习率，直到损失在 $\eta_{\max }$“爆炸”。举例来说，在图 $13.16$ 中，我们发现 $\eta_{\max } \approx 0.1$ 。然后我们将 $\eta_{0}$ 设置为比 $\eta_{\mathrm{max}}$ 稍小的值（如小于$10$倍大小）。

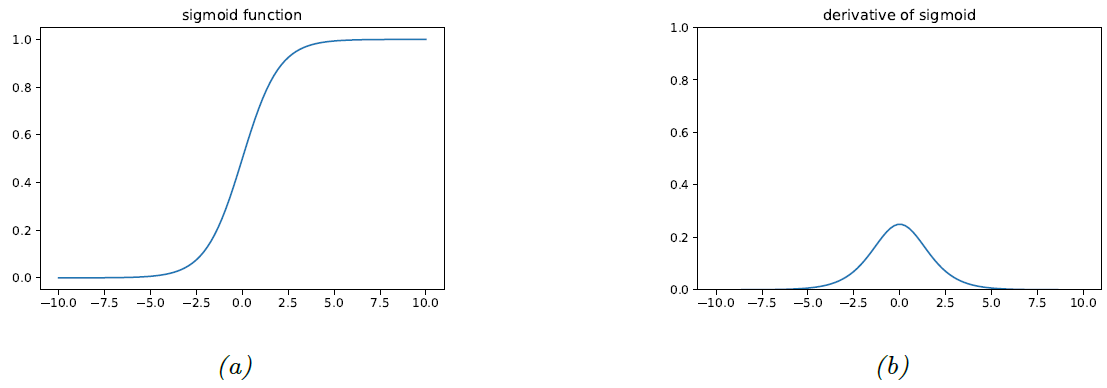
sigmoid_act

图 $13.17$: $(a)$ $\textrm{sigmoid}$ 激活函数。 $(b)$ 对应的导数。

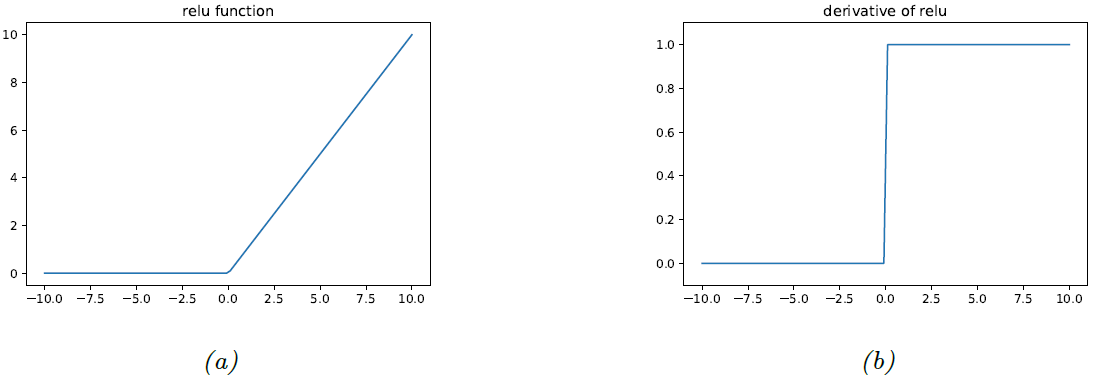
relu_act

图 $13.18$: $(a)$ $\textrm{ReLU}$ 激活函数。 $(b)$ 对应的导数。

13.4.2 梯度消失问题

在某些 $\textrm{DNN}$ 中，梯度信号在通过网络传播回来时会变为 $0$，进而阻止了学习过程的继续。这就是所谓的梯度消失问题（$\textrm{vanishing gradient problem}$）[GB10]⁵⁰。

为了了解它为什么会发生，让我们考虑一下 $\textrm{sigmoid}$ 激活函数 $\varphi(a)=\sigma(a)=\frac{1}{1+\exp (-a)} \tag{13.74}$ 上式的导数为 $\varphi^{\prime}(a)=\sigma(a)(1-\sigma(a)) \tag{13.75}$ 现在考虑网络层 $\mathbf{z}=\sigma(\mathbf{W} \mathbf{x})$ 。假设这是最后一层，所以 $\delta=\frac{\partial \mathbf{f}(\mathbf{x}, \boldsymbol{\theta})}{\partial \mathbf{x}} = \mathbf{z}(1-\mathbf{z})$ 。使用 $13.3.3$ 节中的结果，我们发现损失函数关于 $\mathbf{x}$ 的梯度为： $\frac{\partial \mathcal{L}}{\partial \mathbf{x}}=\delta^{\top} \mathbf{W}=\mathbf{W}^{\top} \mathbf{z}(1-\mathbf{z}) \tag{13.76}$ 并且 $\frac{\partial \mathcal{L}}{\partial \mathbf{W}}=\delta \mathbf{x}^{\top}=\mathbf{z}(1-\mathbf{z}) \mathbf{x}^{\top} \tag{13.77}$ 如果权重被初始化为一个很大的值（正或负），那么 $\mathbf{W}{\mathrm{x}}$ 的（某些分量）很容易取很大的值，因此 $\mathbf{z}$ 将接近 $\textrm{sigmoid}$ 的饱和值 $0$ 或 $1$，如图 $\textrm{13.17a}$ 所示。在任何一种情况下，我们都可以看到梯度将变为 $0$，如图 $\textrm{13.17b}$ 所示。

解决梯度消失问题的标准方案是使用 $\textrm{ReLU}$ 激活函数。所以假设我们使用 $\mathbf{z}=\operatorname{ReLU}\left(\mathbf{Wx}\right)$，其中 $\operatorname{ReLU}(a)=\max (a, 0) \tag{13.78}$ 梯度为 $\operatorname{ReLU}^{\prime}(a)=\mathbb{I}(a>0) \tag{13.79}$ 假设这是最后一层，所以 $\delta=\frac{\partial \mathbf{f}(\mathbf{x}, \boldsymbol{\theta})}{\partial \mathbf{x}}=\mathbb{I}(\mathbf{z}>\mathbf{0})$ 。使用 $13.3.3$ 节的结果，发现激活函数的局部梯度为 $\frac{\partial \mathcal{L}}{\partial \mathbf{x}}=\delta^{\top} \mathbf{W}=\mathbf{W}^{\top} \mathbb{I}(\mathbf{z}>\mathbf{0}) \tag{13.80}$ 并且 $\frac{\partial \mathcal{L}}{\partial \mathbf{W}}=\delta \mathbf{x}^{\top}=\mathbb{I}(\mathbf{z}>0) \mathbf{x}^{\top} \tag{13.81}$ 如果权重初始化为较大的负值，会容易导致 $\mathbf{Wx}$ 变成较大的负值，进而导致 $\mathbf{z}=0$，如图 $\textrm{13.18a}$ 所示。这将会导致关于权重的梯度等于 $0$，如图 $\textrm{13.18b}$ 所示。算法将永远无法摆脱该局部解，所以对应的激活单元将永远被关闭。这被称为 “$\textrm{dead relu}$” 问题。这个问题可以通过使用 $\operatorname{ReLU}$ 的非饱和变体进行解决，正如我们在 $13.2.3$ 节中所讨论的那样。

13.4.3 训练深度模型的困难

当我们训练非常深的模型的时候，梯度往往会趋向于变得过小（梯度消失问题，$\textrm{vanishing gradient problem}$）或过大（梯度爆炸问题，$\textrm{exploding gradient problem}$），因为误差信号在经过一系列层的时候会被放大或者抑制。（$\textrm{RNNs}$ 应用于较长序列时，也会出现这种问题，我们将会在 $15.2.5$ 节解释。）

为了更加深入地理解这个问题，考虑损失关于第 $l$ 层中某个节点的梯度： $\frac{\partial \mathcal{L}}{\partial \mathbf{z}_{l}}=\frac{\partial \mathcal{L}}{\partial \mathbf{z}_{l+1}} \frac{\partial \mathbf{z}_{l+1}}{\partial \mathbf{z}_{l}}=\mathbf{J}_{l} \mathbf{g}_{l+1} \tag{13.82}$ 其中 $\mathbf{J} _{l}=\frac{\partial \mathbf{z} _{l+1}}{\partial \mathbf{z} _{l}}$ 为雅各比矩阵，$\mathbf{g} _{l+1}=\frac{\partial \mathcal{L}}{\partial \mathbf{z} _{l+1}}$ 表示下一层的梯度。如果 $\mathbf{J} _l$ 在不同的层都是一个常数，那么显然最后一层的梯度 $\mathbf{g} _L$ 对第 $l$ 层的贡献为 $\mathbf{J}^{L-l} \mathbf{g} _{L}$ 。所以系统的行为将依赖于 $\mathbf{J}$ 的特征向量。

尽管 $\mathbf{J}$ 是一个实数矩阵，但它不是（一般情况下）对称的，所以它的特征值和特征向量可能是复数，其中的虚数部分对应着振荡的行为。令 $\lambda$ 表示 $\mathbf{J}$ 的 谱半径（$\textrm{spectral radius}$），即特征值的绝对值的最大值。如果它大于 $1$，梯度将发生爆炸；如果小于 $1$，梯度将会消失。（类似地， $\mathbf{W}$ 的谱半径，连接着 $\mathbf{z} _l$ 和 $\mathbf{z} _{l+1}$，决定了在前向模式下动态系统的稳定性。）

梯度爆炸问题可以通过 梯度截断（$\textrm{gradient clipping}$）来进行改善，当梯度过大时，我们将它的幅值进行截断，举例来说，使用 $\mathrm{g}^{\prime}=\min \left(1, \frac{c}{\|\mathrm{~g}\|}\right) \mathrm{g} \tag{13.83}$ 通过这种方式，$\mathrm{g}^{\prime}$ 的范数将不会超过 $c$，但其更新方向始终与 $\mathrm{g}$ 相同。

然而，梯度消失问题却很难解决。有如下几种解决方案：

更改模型结构，从而使得梯度的更新通过相加而不是相乘的形式；见 $13.4.4$ 节。
更改模型结构，使每一层的激活值标准化，从而使整个数据集上的激活值的分布在训练期间保持一致；见 $13.4.5$ 节。
小心地选择参数的初始化值；见 $13.4.6$ 节。

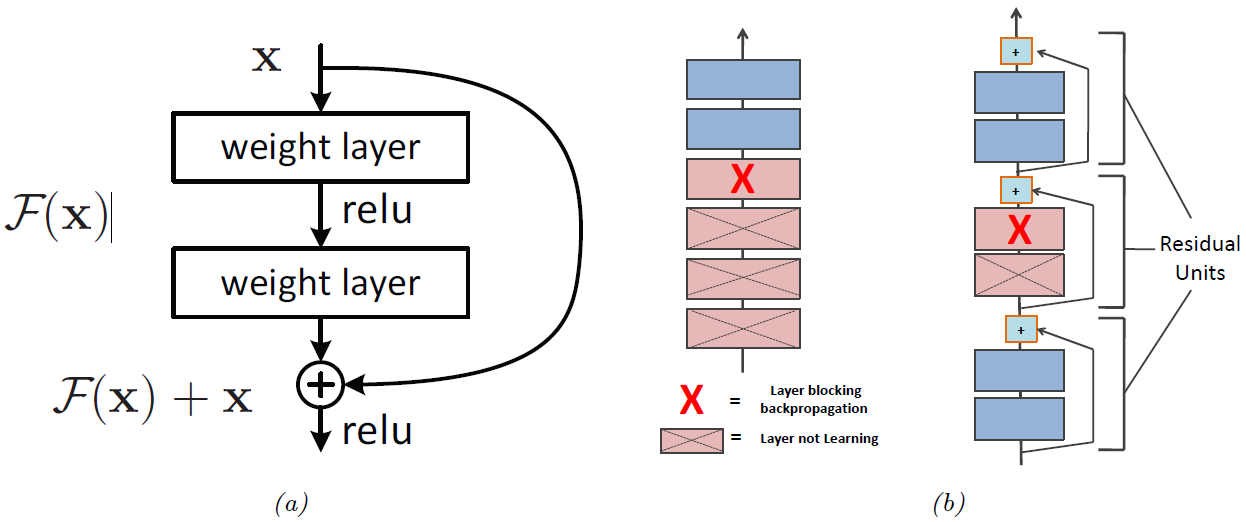
res_block

图$13.19$: $(a)$ 残差模块的示意图。$(b)$ 残差模块有利于深度网络训练的原因。图形来自于 [Ger19]³ 的图 $14.16$。

13.4.4 残差连接

对于 $\textrm{DNNs}$ 而言，一种解决梯度消失问题的方案是使用 残差网络（$\textrm{residual network, ResNet}$）[He+16a][He16a]。该前向网络中的每一层的形式是一个残差模块（$\textrm{residual block}$），定义为 $\mathcal{F}_{l}^{\prime}(\mathrm{x})=\mathcal{F}_{l}(\mathrm{x})+\mathrm{x} \tag{13.84}$ 其中 $\mathcal{F} _{l}$ 是一个很浅的非线性映射函数（比如：线性层—激活层—线性层）。 $\mathcal{F} _{l}$ 函数计算需要添加到输入 $\mathrm{x}$ 中以生成所需输出的残差项或增量；相较于直接让网络学习如何预测输出，学习在输入的基础上产生的小扰动通常更加容易。（如第 $14.3.2.4$ 节所述，残差连接通常与 $\textrm{CNN}$ 一起使用，但也可用于 $\textrm{MLP}$。）

含有残差连接的模型与没有残差连接的模型具有相同的参数数量，但是训练起来比较容易。原因是梯度可以直接从输出传递到浅层，如图 $\textrm{13.19b}$ 所示。要说明这一点，值得注意的是，输出层的激活可以通过使用任意浅层 $l$ 的输出得到： $\mathrm{z}_{L}=\mathrm{z}_{l}+\sum_{i=l}^{L-1} \mathcal{F}_{i}\left(\mathrm{z}_{i} ; \boldsymbol{\theta}_{i}\right) \tag{13.85}$ 所以我们可以计算损失关于 $l$ 层的梯度： $\begin{align} \frac{\partial \mathcal{L}}{\partial \boldsymbol{\theta}_{l}} &=\frac{\partial \mathbf{z}_{l}}{\partial \boldsymbol{\theta}_{l}} \frac{\partial \mathcal{L}}{\partial \mathbf{z}_{l}} \tag{13.86} \\ &=\frac{\partial \mathbf{z}_{l}}{\partial \boldsymbol{\theta}_{l}} \frac{\partial \mathcal{L}}{\partial \mathbf{z}_{L}} \frac{\partial \mathbf{z}_{L}}{\partial \mathbf{z}_{l}} \tag{13.87} \\ &=\frac{\partial \mathbf{z}_{l}}{\partial \boldsymbol{\theta}_{l}} \frac{\partial \mathcal{L}}{\partial \mathbf{z}_{L}}\left(1+\sum_{i=l}^{L-1} \frac{\partial f\left(\mathbf{z}_{i} ; \boldsymbol{\theta}_{i}\right)}{\partial \mathbf{z}_{l}}\right) \tag{13.88} \\ &=\frac{\partial \mathbf{z}_{l}}{\partial \boldsymbol{\theta}_{l}} \frac{\partial \mathcal{L}}{\partial \mathbf{z}_{L}}+\text { otherterms } \tag{13.89} \end{align}$ 所以我们发现第 $l$ 层的梯度可以直接取决于第 $L$ 层的梯度，并与网络的深度无关。

13.4.5 Batch normalization

对 $\textrm{DNN}$ 结构的另一个普遍的修改是添加一个层，该层可以确保层内激活值的分布均值为 $0$ 和方差为 $1$。这被称为批处理规范化 （$\mathrm{batch\ normalization, BN}$）[IS15]⁵¹。

更准确地说，我们将样本 $n$ （在某一层）的激活向量 $\mathbf{z} _n$ （或者是预激活向量 $\mathbf{a} _n$）替换为 $\tilde{\mathbf{z}} _{n}$ ，计算方式为：

$\begin{align} \tilde{\mathbf{z}}_{n} & =\pmb{\gamma} \odot \hat{\mathbf{z}}_{n}+\pmb{\beta} \tag{13.90} \\ \hat{\mathbf{z}}_{n} & =\frac{\mathbf{z}_{n}-\pmb{\mu}_{\mathcal{B}}}{\sqrt{\pmb{\sigma}_{\mathcal{B}}^{2}+\epsilon}} \tag{13.91} \\ \pmb{\mu}_{\mathcal{B}} & =\frac{1}{|\mathcal{B}|} \sum_{\pmb{\mathbf{z}} \in \mathcal{B}} \mathbf{z} \tag{13.92} \\ \pmb{\sigma}_{\mathcal{B}}^{2} & =\frac{1}{|\mathcal{B}|} \sum_{\pmb{\mathbf{z}} \in \mathcal{B}}\left(\mathbf{z}-\pmb{\mu}_{\mathcal{B}}\right)^{2} \tag{13.93} \end{align}$ 其中 $\mathcal{B}$ 为包含样本 $n$ 的批次，$\pmb{\mu} _\mathcal{B}$ 为该批次数据激活值的均值⁵²，$\pmb{\sigma} _{\mathcal{B}}^{2}$ 为对应的方差， $\hat{\mathbf{z}} _{n}$ 表示标准化后的激活向量，$\tilde{\mathbf{z}} _{n}$ 表示经过平移和缩放后的结果（$\mathrm{BN}$ 层的输出），$\pmb{\beta}$ 和 $\pmb{\gamma}$ 表示该层的可学习参数， $\epsilon>0$ 是一个值很小的常数。考虑到 $\mathrm{BN}$ 是可微的，我们可以很容易地将梯度反传到该层的输入和 $\mathrm{BN}$ 的参数 $\pmb{\beta}$ 和 $\pmb{\gamma}$。

对于输入层， $\mathrm{batch\ normalization}$ 等价于我们在 $10.2.8$ 节讨论的常规的标准化过程。值得注意的是，输入层的均值和方差只需要计算一次，因为数据是静态的。然而，中间层的经验均值和方差是不断改变的，因为参数一直在更新。（这通常被称为 “内协变量漂移”（$\mathrm{internal\ covariate\ shift}$）。这就是我们需要对每一个批次重新计算 $\pmb{\mu}$ 和 $\pmb{\sigma}^2$ 的原因。

$\mathrm{BN}$ 的作用（在训练速度和稳定性方面）是非常显著的，尤其是对于深度 $\textrm{CNNs}$。具体的原因还不是很清楚，但 $\mathrm{BN}$ 似乎使优化曲面变得更加平滑 [San+18]⁵³。同时它也降低了对学习率的敏感性 [ALL18]⁵⁴。除了计算方面的优势，它还具备统计上的优势。特别地， $\mathrm{BN}$ 更像一个正则器；事实上，它可以被证明是相当于一种形式的近似贝叶斯推理 [TAS18][^TAS18];[Luo+19][^Luo19]。

然而，依赖于小批量数据会导致几个问题。首先，在小批量训练时，它可能会导致参数估计不稳定，尽管该方法的最新版本批量重规范化（$\textrm{batch renormalization}$）[Iof17][^Iof17]部分地解决了这个问题。其次，$\mathrm{BN}$ 在推理阶段需要进行一些调整，因为在测试阶段时的 $\textrm{batch size}$ 可能是 $1$。具体的测试过程为：在训练之后，计算训练集中所有样本在第 $l$ 层的 $\pmb{\mu}_l$ 和 $\pmb{\sigma}_l^2$，然后”冻结“这些参数，并将这些值添加到该层其他参数的列表中，即 $\pmb{\beta}_l$ 和 $\pmb{\gamma}_l$ 。在测试阶段，我们利用这些冻结的参数计算 $\pmb{\mu}_l$ 和 $\pmb{\sigma}_l^2$，而不是从测试批次中计算统计量。（所以在使用包含 $\mathrm{BN}$ 的模型中，我们需要指定模型是用于训练还是测试。）

The standard approach to this is as follows: after training, compute $\pmb{\mu}_l$ and $\pmb{\sigma}_l^2$ for layer $l$ across all the examples in the training set, and then “freeze” these parameters, and add them to the list of other parameters for the layer, namely $\pmb{\beta}_l$ and $\mathbf{\gamma}_l$. At test time, we then use these frozen training values for $\pmb{\mu}_l$ and $\pmb{\sigma}_l^2$ , rather than computing statistics from the test batch. (Thus when using a model with $\textrm{BN}$, we need to specify if we are using it for inference or training.)

为了提高推理速度，我们可以将冻结后的批处理规范层与前一层结合起来。特别地，假设前一层计算 $\mathbf{XW}+\mathbf{b}$；将其与 $\mathrm{BN}$ 组合 $\pmb{\gamma}\ \odot(\mathbf{XW+b-\pmb{\mu}})/\pmb{\sigma}\ +\ \pmb{\beta}$。如果我们定义 $\mathbf{W}^{\prime}=\gamma \odot \mathbf{W} / \sigma$ 和 $\mathbf{b}^{\prime}=\gamma \odot(\mathbf{b}-\boldsymbol{\mu}) / \sigma+\boldsymbol{\beta}$ ，然后我们可以将组合的层写成 $\mathbf{X} \mathbf{W}^{\prime}+\mathbf{b}^{\prime}$。这被称为 融合批规范（$\mathrm{fused\ batchnorm}$）。在训练过程中，可以开发类似的技巧来加速 $\mathrm{BN}$ 计算[Jun+19][^Jun19]。

13.4.6 参数初始化

由于 $\textrm{DNN}$ 训练的目标函数是非凸的， $\textrm{DNN}$ 参数的初始化方式对我们最终能够得到的优化解以及训练优化过程的难易程度（即，信息在前向与反向传播过程中的有益程度）有很大的影响。在本节的剩余部分，我们将介绍一些用于初始化参数的常见的启发式方法。

13.4.6.1 启发式

在 [GB10]⁵⁰ 中，他们表明从标准正态中采样得到的参数会导致输出的方差远大于输入的方差，从而导致梯度爆炸。为了解决这个问题，他们提出从均值为 $0$ ，方差为 $\sigma^{2}=1 / \text{fan} _{\text{avg}}$ 的高斯分布中采样参数，其中$ \text{fan} _\text{avg} = (\text{fan} _\text{in} + \text{fan} _\text{out})/2$，其中 $\text{fan} _\text{in}$ 是一个单元的扇入（传入连接数），$\text{fan} _\text{out}$是单元的扇出（传出连接数）。这种方法被称为 $\textbf{Xavier}$ 初始化或 $\textbf{Glorot}$ 初始化，以 [GB10]⁵⁰ 的第一作者的名字命名。如果我们使用 $\sigma^{2}=1 / \text{fan} _{\text{in}}$，我们会得到一种称为 $\textbf{LeCun}$ 初始化的方法，以 $\textrm{Yann LeCun}$ 的名字命名，他于 $1990$ 年代提出该方法，等效于 $\text{fan} _\text{in} = \text{fan} _\text{out} $ 时的 $\textbf{Glorot}$ 初始化。如果我们用 $\sigma^{2}=2 / \text{fan} _{\text{in}}$，该方法称为 $\textbf{He}$初始化，得名于$\text{Kaiming He}$，他在[He+15]⁵⁵中提出了该方法。初始化方法的最佳选择取决于所使用的激活函数。对于线性、$\text{tanh}$、$\text{logistic}$ 和 $\text{softmax}$ 激活函数，推荐使用 $\textbf{Glorot}$。对于 $\text{ReLU}$ 及其变体，推荐使用 $\text{He}$。对于 $\text{SELU}$，推荐 $\text{LeCun}$。有关更多启发式的方法，请参考 [Gér19]³。

Ximing He ——> Kaiming He

我们也可以使用一种数据驱动的参数初始化方法。举例来说，[MM16]⁵⁶ 提出一种简单而且有效的策略，被称为 $\textbf{layer-sequential unit-variance (LSUV)}$ 初始化，工作原理如下。首先我们对每一层（全连接或卷积层）的权重初始化一个 [SMG14]⁵⁷ 中提出的正交矩阵。（该正交矩阵可以通过如下方式获得，首先从分布 $\mathbf{w} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ 中进行采样，并将 $\mathbf{w}$ $\text{reshape}$ 为矩阵 $\mathbf{W}$，然后使用 $\textrm{QR}$ 或者 $\textrm{SVD}$ 分解获取矩阵的正交基。）接着，对于每一层 $l$，我们计算一个 $\textrm{minibatch}$ 的激活值的方差 $v_l$；然后使用 $\mathrm{W} _{l}:=\mathrm{W} _{l} / \sqrt{v _{l}}$ 进行重缩放。该策略可以看作是正交初始化与 $\textrm{batch normalization}$ 的组合，而后者只需要针对第一个 $\textrm{mini-batch}$ 进行计算。实验表明，这样的 $\textrm{normalization}$ 已经足够，并且该方法要快于完全使用 $\textrm{batch normalization}$。

另一种方法被称为 $\mathbf{fixup}$ [ZDM19]⁵⁸。该方法可以用于训练没有 $\textrm{batchnorm}$ 的非常深的残差网络。

13.4.6.2 一种函数空间视角

考虑一个含有 $L$ 个隐藏层和 $1$ 个线性输出层的 $\textrm{MLP}$： $f(\mathbf{x} ; \boldsymbol{\theta})=\mathbf{W}_{L}\left(\cdots \varphi\left(\mathbf{W}_{2} \varphi\left(\mathbf{W}_{1} \mathbf{x}+\mathbf{b}_{1}\right)+\mathbf{b}_{2}\right)\right)+\mathbf{b}_{L} \tag{13.94}$ 我们可以假设模型参数分别服从如下分布： $\mathbf{W}_{\ell} \sim \mathcal{N}\left(0, \alpha_{\ell}^{2} \mathbf{I}\right), \mathbf{b}_{\ell} \sim \mathcal{N}\left(0, \beta_{\ell}^{2} \mathbf{I}\right) \tag{13.95}$ 我们可以对上述分布进行重参数化： $\mathbf{W}_{\ell}=\alpha_{\ell} \eta_{\ell}, \eta_{\ell} \sim \mathcal{N}(0, \mathbf{I}), \mathbf{b}_{\ell}=\beta_{\ell} \epsilon_{\ell}, \epsilon_{\ell} \sim \mathcal{N}(0, \mathbf{I}) \tag{13.96}$ 所以每一种先验超参都指定了一个如下的随机函数： $f(\mathrm{x} ; \boldsymbol{\alpha}, \boldsymbol{\beta})=\alpha_{L} \eta_{L}\left(\cdots \varphi\left(\alpha_{1} \eta_{1} \mathrm{x}+\beta_{1} \epsilon_{1}\right)\right)+\beta_{L} \epsilon_{L} \tag{13.97}$ 为了理解这些超参数的影响，我们可以从这些先验中采样得到 $\textrm{MLP}$ 的参数，并且绘制出最终的随机函数。我们使用 $\textrm{sigmoid}$ 非线性函数，所以 $\varphi(a)=\sigma(a)$。我们考虑 $L=2$ 层的网络，所以 $\mathbf{W}_1$ 对应 $\text{input-to-hidden}$ 的权重， $\mathbf{W}_2$ 对应 $\text{hidden-to-output}$ 的权重。我们假设输入和输出为标量，所以我们最终可以随机生成非线性映射 $f: \mathbb{R} \rightarrow \mathbb{R}$。

图 $13.20(a)$ 展示了一些采样得到的函数，其中 $\alpha_{1}=5, \beta_{1}=1, \alpha_{2}=1, \beta_{2}=1$ 。在图 $13.20(b)$ 中我们增加了 $\alpha_1$；这使得第一层的权重变得更大，导致 $\textrm{S}$ 型函数的形状更陡（与图 $10.2$ 相比）。在图 $13.20(c)$ 中，我们增加 $\beta_1$；这使得第一层的偏置更大，使得函数的中心更多地向左右两侧移动。图 $13.20(d)$中，我们增加 $\alpha_2$，使得第二层的线性层权重更大，导致函数变得更加 “扭曲”(wiggly) （对输入的变化更加敏感，所以导致更大的动态范围）

上述结果只是针对 $\textrm{sigmoidal}$ 激活函数的情况。 $\textrm{ReLU}$ 函数的结果可能不一样。举例来说， [WI20, App.E]⁵⁹ 表明，对于包含 $\textrm{ReLU}$ 激活单元的 $\text{MLPs}$ ，如果我们令 $\beta_l=0$，那么所有的偏置项都为 $0$，那么改变 $\alpha_l$ 的影响只是对输出进行尺度缩放。为了说明这一点，注意到公式 $(13.97)$ 可以简化为 $\begin{align} f(\mathrm{x} ; \alpha, \beta=0) &=\alpha_{L} \eta_{L}\left(\cdots \varphi\left(\alpha_{1} \eta_{1} \mathrm{x}\right)\right)=\alpha_{L} \cdots \alpha_{1} \eta_{L}\left(\cdots \varphi\left(\eta_{1} \mathrm{x}\right)\right) \tag{13.98} \\ &=\alpha_{L} \cdots \alpha_{1} f(\mathrm{x} ;(\alpha=1, \beta=0)) \tag{13.99} \end{align}$ 其中我们使用了 $\text{ReLU}$ 的规律， $\varphi(\alpha z)=\alpha \varphi(z)$ 对任意正数 $\alpha$ 都成立，$\varphi(\alpha z)=0$ 对于任意的负数 $\alpha$ 都成立（因为预激活值 $z \gt 0$）。一般情况下，输入信号在一个随机初始化的网络中进行前向和反向传播时到底会发生什么情况，通常由 $\alpha$ 和 $\beta$ 决定，更多细节可参考 [Bah+20]⁴⁵。

从上面的分析中我们发现， $\text{DNN}$ 中参数的不同分布对应于函数的不同分布。所以模型的随机初始化更像是从先验知识中进行采样。当神经网络趋向于无限宽时，我们可以推导出该先验分布的解析解：这被称为 神经网络高斯过程（$\textrm{neural network Gaussian process}$）,我们将会在本书的第二册进行解释 [Mur22]⁶⁰。

13.5 正则化

在 $13.4$ 节，我们从计算角度讨论了在训练（大型）神经网络过程中的一些问题。本节，我们会从统计学的角度对这个问题展开讨论。特别地，我们将集中讨论避免过拟合的方法。关于这一点十分重要，因为较大的神经网络很容易具有百万级的参数。

13.5.1 提前终止 (Early stopping)

或许避免过拟合最好的方式就是提前终止 ($\textrm{early stopping}$)，这是一种启发式的方法，当模型在验证集上的错误率开始增加时终止对模型的训练（见图 $4.7$）。该方法之所以奏效，是因为我们限制了优化算法将训练样本中的信息传递到模型参数的能力，正如 [AS19]⁶¹ 所解释的。

13.5.2 权重衰减 (Weight decay)

一种常见的避免过拟合的方式是为参数赋予一个先验分布，然后使用 $\textrm{MAP}$ 估计。通常情况下对模型的权重使用高斯先验 $\mathcal{N}\left(\mathbf{w} \mid \mathbf{0}, \alpha^{2} \mathbf{I}\right)$，对偏置使用 $\mathcal{N}\left(\mathbf{b} \mid \mathbf{0}, \beta^{2} \mathbf{I}\right)$。（参考 $13.4.6.2$ 节对该先验的讨论）这等价于目标函数的 $l_2$ 正则。在神经网络的文献中，被称为 权重衰减 （$\textrm{weight decay}$），因为该方法鼓励值小的权重，即更加简单的模型，正如岭回归的原理一样（$11.3$ 节）。

13.5.3 稀疏化 DNNs

考虑到神经网络中包含很多权重，通常鼓励稀疏化是有益的。这将允许我们进行模型压缩（$\textrm{model compression}$），从而可以节省存储和时间。为了实现这一点，我们可以使用 $l_1$ 正则（$11.5$ 节），或者 $\textrm{ARD}$ （$11.6.6$ 节），或者 $\textrm{spike and slab}$ 先验（$11.6.4.1$ 节），或者 $\textrm{horseshoe}$ 先验（$11.6.4.3$ 节）等。（[GEH19]⁶² 给出了相关知识的综述）。

考虑一个具体例子，图 $13.21$ 展示了一个 $5$ 层 $\textrm{MLP}$，该模型已经对 $1$ 维数据进行了拟合，并且对权重使用了 $l_1$ 正则。我们发现最终的图形拓扑结构是稀疏的。当然，存在很多稀疏化估计的方法也是可行的。

尽管直觉上稀疏化的拓扑结构很具有吸引力，但实际上这种方法却很少被普遍使用，因为主流的 $\textrm{GPUs}$ 只针对稠密（$\textit{dense}$）矩阵乘法作了优化，而稀疏矩阵的乘法并没有什么计算上的优势。然而，如果我们使用能够鼓励组 ($\textit{group}$) 稀疏化的方法，我们对模型中的整个层都进行减枝操作。这将导致 块稀疏化（$\textit{block sparse}$）权重矩阵，这将有利于计算上的加速和存储上的节约（参考 [Sca+17]⁶³;[Wen+16]⁶⁴;[MAV17]⁶⁵;[LUW17]⁶⁶）。

13.5.4 Dropout

假设我们依概率 $p$ 随机的将每个节点的输出连接关闭，如图 $13.22$ 所示。该技术被称为 $\textbf{dropout}$ [Sri+14]⁶⁷。

$\textrm{Dropout}$ 可以显著地降低过拟合风险并且被广泛使用。直觉上，该技术之所以有效的原因在于，它阻止了隐藏节点间的复杂的互适应性。换句话说，每一个节点必须表现良好，及时某些其他的节点被随机的取消。这将阻止节点之间学习到复杂但脆弱的依赖关系⁶⁸。一个更加正式的解释，从高斯尺度混合先验角度进行分析，该解释可参考[NHLS19]⁶⁹。

我们可以将该技术视作是一种对权重的含噪估计 $\theta_{l i j}=w_{l i j} \epsilon_{l i}$，其中 $\epsilon_{l i} \sim \operatorname{Ber}(1-p)$ 为伯努利噪声项。（所以如果我们采样 $\epsilon_{l i}=0$ , 那么所有连接 $l-1$ 层的节点 $i$ 与 $l$ 层的 $j$ 节点的权重将被设置为 $0$。）在测试阶段，我们通常将噪声关闭，这等价于令 $\epsilon_{l i}=1$ 。为了获得无噪声权重的估计值，我们应该使用 $w_{l i j}=\theta_{l i j} / \mathbb{E}\left[\epsilon_{l i}\right]$，所以测试阶段权重的期望值与训练阶段的期望值保持一致。对于伯努利噪声，我们有 $\mathbb{E}[\epsilon]=1-p$ ，所以在测试阶段我们应该除以 $1-p$。

th enoise -> the noise

然而，我们也可以在测试阶段使用 $\textrm{dropout}$。其最终的结果为网络的$\textrm{ensemble}$，每一个子网络对应一个稀疏的图结构。这被称为 $\textbf{Monte Carlo dropout} $[GG16]⁷⁰;[KG17]⁷¹，具体形式为: $p(\mathbf{y} \mid \mathbf{x}, \mathcal{D}) \approx \frac{1}{S} \sum_{s=1}^{S} p\left(\mathbf{y} \mid \mathbf{x}, \hat{\mathbf{W}} \epsilon^{s}+\hat{\mathbf{b}}\right) \tag{13.100}$ 其中 $S$ 为采样样本的数量，$\hat{\mathbf{W}} \epsilon^{s}$ 表明我们将所有估计的矩阵与一个经随机采样得到的噪声向量进行了矩阵乘。这种方式通常可以提供一个对贝叶斯后验预测分布 $p(\mathbf{y} \mid \mathbf{x}, \mathcal{D})$ 的好的近似，尤其是在噪声比是被优化过的情况下 [GHK17]⁷²。

13.5.5 贝叶斯神经网络

主流的 $\textrm{DNNs}$ 通常使用（含惩罚项）最大似然估计的目标函数来搜寻一种参数的配置。然而，对于特别大的模型，其参数量往往大于数据量，所以可能存在多种可能的模型，它们对训练集的拟合情况都很好，但在泛化性能上具有差异性。通过获取后验分布中的不确定性通常是有用的。我们可以关于模型参数计算边缘概率分布实现这一点 $p(\mathbf{y} \mid \mathbf{x}, \mathcal{D})=\int p(\mathbf{y} \mid \mathbf{x}, \boldsymbol{\theta}) p(\boldsymbol{\theta} \mid \mathcal{D}) d \boldsymbol{\theta} \tag{13.101}$ 上述结果被称为 $\textbf{Bayesian neural network}$ 或者 $\textbf{BNN}$。它可以被认识是一个含不同权重的神经网络的无限集成。通过对参数求边缘分布，我们可以避免过拟合[Mac95]⁷³。贝叶斯边缘化对于大型神经网络具有挑战性，但同样可以获得大幅的性能提升 [WI20]⁵⁹。关于$\textbf{Bayesian deep learning}$ 的更多细节，可以参考书籍 [Mur22]⁶⁰。

13.6 其他形式的前馈网络

13.6.1 径向基函数网络

考虑单层神经网络，其中的隐藏层的输入定义为： $\boldsymbol{\phi}(\mathbf{x})=\left[\mathcal{K}\left(\mathbf{x}, \boldsymbol{\mu}_{1}\right), \ldots, \mathcal{K}\left(\mathbf{x}, \boldsymbol{\mu}_{K}\right)\right] \tag{13.102}$ 其中 $\boldsymbol{\mu} {k} \in \mathcal{X}$ 为 $K$ 个质心（$\textrm{centroids}$）或代理（$\textrm{exemplars}$），其中 $\mathcal{K}(\mathbf{x}, \boldsymbol{\mu}) \geq 0$ 为 核函数（$\textrm{kernel function}$）。我们将在 $17.2$ 节讨论关于核函数的细节。此处我们只给出关于 高斯核（$\textrm{Gaussian kernel}$）的例子 $\mathcal{K}_{\text {gauss }}(\mathbf{x}, \mathbf{c}) \triangleq \exp \left(-\frac{1}{2 \sigma^{2}}\|\mathbf{c}-\mathbf{x}\|_{2}^{2}\right) \tag{13.103}$ 参数 $\sigma$ 被称为核的带宽（$\textrm{bandwidth}$）。需要注意的是高斯核具有平移不变性，意味着它只是关于距离 $r=|\mathbf{x}-\mathbf{c}|{2}$ 的函数，所以我们可以等价地写成 $\mathcal{K}_{\text {gauss }}(r) \triangleq \exp \left(-\frac{1}{2 \sigma^{2}} r^{2}\right) \tag{13.104}$ 所以它又被称为 径向基函数核（$\textrm{ radial basis function kernel, RBF kernel}$）。

如果一个单层神经网络使用式 $13.102$ 定义形式作为隐藏层（包含 $\textrm{RBF}$ 核），则该神经网络被称为 $\textbf{RBF network}$ [BL88][^BL88]。形式定义为 $p(y\mid\mathbf{x} ; \boldsymbol{\theta})=p\left(y\mid\mathbf{w}^{\top} \boldsymbol{\phi}(\mathbf{x})\right) \tag{13.105}$ 其中 $\boldsymbol{\theta}=(\boldsymbol{\mu}, \mathbf{w})$ 。如果质心 $\boldsymbol{\mu}$ 是固定的，我们可以使用（含正则项的）最小二乘方法求解权重 $\mathbf{w}$ 的最优解，如第 $11$ 章讨论的。如果质心是未知的，我们使用无监督聚类方法对质心进行估计，如 $\textrm{K-means}$（$21.3$ 节）。作为替代方案，我们可以为训练集中的每一个数据关联一个质心，即 $\boldsymbol{\mu} _{n}=\mathbf{x} _{n}$，此时 $K=N$，这是非参数化模型（$\textrm{ non-parametric model}$）的例子，因为参数的数量随着数据的数量增加（这种情况下呈线性增长关系），而非独立于数据量 $N$。如果 $K=N$，模型可以完美地拟合数据，同时也有可能发生过拟合。然而，通过确保输出的权重矩阵 $\mathbf{w}$ 稀疏化，模型可以只使用输入的样本中的有限的子集，这被称为 稀疏核机器（$\textrm{sparse kernel machine}$），具体细节将在 $17.6.1$ 和 $17.5$ 节讨论。另一种避免过拟合的方式是使用贝叶斯方式，通过对权重 $\mathbf{w}$ 积分；这将引出另一个模型，被称为 高斯过程（$\textrm{Gaussian process}$），我们将在 $17.3$ 节讨论该模型的更多细节。

13.6.1.1 RBF网络用于回归

我们可以使用 $\textrm{RBF}$ 网络完成回归任务，定义为 $p(y \mid \mathbf{x}, \boldsymbol{\theta})=\mathcal{N}\left(\mathbf{w}^{T} \boldsymbol{\phi}(\mathbf{x}), \sigma^{2}\right)$ 。举例来说，图 $13.24$ 展示了 $\textrm{RBF}$ 拟合 $1$ 维数据的结果，其中我们使用了 $K=10$ 个均匀分布的 $\textrm{RBF}$ 代理，但相应的带宽从小到大变化。越小的带宽导致越畸变的函数，因为只有当点 $\mathbf{x}$ 接近某个代理 $\boldsymbol{\mu}_{k}$ 时，预测的函数值才会是非零值。如果带宽非常大，设计矩阵将退化为元素值为 $1$ 的常数矩阵，因为每个点与每个代理的距离相同，所以最终的函数只是一条直线。

13.6.1.2 RBF网络用于分类

我们可以使用 $\textrm{RBF}$ 网络完成二分类任务，定义为 $p(y \mid \mathbf{x}, \boldsymbol{\theta})=\operatorname{Ber}\left(\mathbf{w}^{T} \boldsymbol{\phi}(\mathbf{x})\right)$ 。作为一个例子，考虑数据来源于异或函数。这是一个具有二个位输入的二值函数。真实标签如图 $13.23(a)$ 所示。在图 $13.1(b)$ 中，我们展示了一些通过抑或函数标记的数据，但我们已经对数据进行了 $\textbf{jitter}$ ⁷⁴，使可视化更加清晰。我们发现我们没有办法将数据分开，哪怕使用阶数为 $10$ 的多项式拟合。然而，使用 $\textrm{RBF}$ 核以及 $4$ 个代理，可以轻松地解决这个问题，如图 $13.1(c)$ 所示。

13.6.2 混合专家

当我们在考虑回归任务时，通常情况下假设输出是一个单峰分布，比如高斯分布或者学生分布，其中的期望和方差是关于输入的某个函数，举例， $p(\mathbf{y} \mid \mathbf{x})=\mathcal{N}\left(\mathbf{y} \mid f_{\mu}(\mathbf{x}), \operatorname{diag}\left(\sigma_{+}\left(f_{\sigma}(\mathbf{x})\right)\right)\right) \tag{13.106}$ 其中函数 $f$ 可能是 $\textrm{MLPs}$ （可能包含一些共享的隐藏层单元，如图 $13.7$ 所示）。然而，这种假设对于 $\textbf{one-to-many}$ 函数可能并不奏效，在这种问题中，每个输入可能对应多种可能的输出。

图 $13.25a$ 给出了类似于这个函数的例子。我们发现在图形的中间存在某些 $x$ 对应着两个同样可能的 $y$ 值。在现实世界中，也存在很多类似于这样的问题，比如，从一个图片中预测一个人的$3d$ 姿态 [Bo+08][^Bo08]，对一张黑白图片进行着色 [Gua+17][^Gua17]，预测视频序列的未来帧 [VT17][^VT17]，等等。任务使用单峰输出密度函数并使用最大似然进行训练的模型——哪怕是灵活的非线性模型，比如神经网络——在 $\textrm{one-to-many}$ 问题中都变现得不好，因为这类模型只是输出一个模糊的平均输出。

为了防止回归均值的问题，我们可以使用 条件混合模型（$\textrm{ conditional mixture model }$）。也就是说，我们假设输出是 $K$ 个不同输出的加权混合，对应于每个输入 $\mathbf{x}$ 输出分布的不同峰值。在高斯分布的情况下，即 $\begin{align} p(\mathbf{y} \mid \mathbf{x}) &=\sum_{k=1}^{K} p(\mathbf{y} \mid \mathbf{x}, z=k) p(z=k \mid \mathbf{x}) \tag{13.107} \\ p(\mathbf{y} \mid \mathbf{x}, z=k) &=\mathcal{N}\left(\mathbf{y} \mid f_{\mu, k}(\mathbf{x}), \operatorname{diag}\left(f_{\sigma, k}(\mathbf{x})\right)\right) \tag{13.108} \\ p(z=k \mid \mathbf{x}) &=\operatorname{Cat}\left(z \mid \mathcal{S}\left(f_{z}(\mathbf{x})\right)\right) \tag{13.109} \end{align}$ 其中 $f_{\mu, k}$ 为第 $k$ 个高斯分布的期望，$f_{\sigma, k}$ 为对应的方差项，$f_z$ 预测使用混合元素中的哪一个。该模型被称为 混合专家（$\textrm{mixture of experts, MoE}$）[Jac+91][^Jac91]；[JJ94][^JJ94]; [YWG12][^YWG12]; [ME14][^ME14]。其思想在于，第 $k$ 个子模型 $p(\mathbf{y} \mid \mathbf{x}, z=k)$ 被认为是输入空间中某个区域的“专家”。函数 $p(z=k \mid \mathbf{x})$ 被称为 门函数（$\textrm{gating function}$）决定着使用哪一个专家，该函数依赖于输入值。通过为某个特定输入 $\mathbf{x}$ 指定最有可能的专家，我们可以只用“激活”模型的一个子集。这是 条件计算（$\textrm{conditional computation}$）的一个例子，因为我们根据门控网络的早期计算结果决定运行哪个专家 [Sha+17][^Sha17]。

我们可以使用 $\textrm{SGD}$ 训练模型，或者使用 $\textrm{EM}$ 算法（$5.7.3$介绍了后一种方法的更多细节）。

13.6.2.1 混合线性专家

在这一节中，我们考虑一个简单的例子，其中我们使用线性回归专家和线性分类门控函数，即，模型具有形式： $\begin{align} p(y \mid \mathbf{x}, z=k, \boldsymbol{\theta}) &=\mathcal{N}\left(y \mid \mathbf{w}_{k}^{\top} \mathbf{x}, \sigma_{k}^{2}\right) \tag{13.110} \\ p(z \mid \mathbf{x}, \boldsymbol{\theta}) &=\operatorname{Cat}(z \mid \mathcal{S}(\mathbf{V} \mathbf{x})) \tag{13.111} \end{align}$ 单独的权重项 $p(z=k \mid \mathbf{x})$ 被称为专家 $k$ 对输入 $\mathbf{x}$ 的责任（$\textrm{ responsibility }$）。在图 $13.25b$中，我们发现门控网络如何平滑地将输入空间划分给 $K=3$个专家。

每个专家 $p(y \mid \mathbf{x}, z=k)$ 对应一个线性回归模型，且包含不同的参数。如图 $13.25c$ 所示。

如果我们将专家的加权组合作为输出，我们将得到图 $13.25a$ 中的红色曲线，显然是一个不好的预测结果。如果我们仅仅使用最有可能的专家进行预测（比如，具有最高责任的专家），我们将得到黑色的不连续曲线，显然是更好的预测器。

13.6.2.2 混合密度网络

门控函数和专家可以是任何类型的条件概率模型，而不仅仅是一个线性模型。如果我们都使用 $\textrm{DNNs}$，最终将得到一个被称为 混合密度网络（$\textrm{mixture density network, MDN}$）[Bis94][^Bis94]; [ZS14][^ZS14] 或者 深度混合专家（$\textrm{deep mixture of experts}$）[CGG17][^CGG17]。图 $13.26$ 给出了一个模型的草图。

13.6.2.3 层次 MOEs

如果每个专家本身就是一个 $\textrm{MoE}$ 模型，最终的模型将被称为 层次混合专家（$\textrm{hierarchical mixture of experts}$）[JJ94][^JJ94]。图 $13.27$ 给出了层次为 $2$ 的模型结构示意图。

具有 $L$ 级的 $\textrm{HME}$ 可以被认为是深度为L的“软”决策树，其中每个示例都通过树的每个分支，并且最终的预测是加权平均（我们将在 $18.1$ 节讨论决策树）

$\textrm{[HG20]}$: J. Howard and S. Gugger. Deep Learning for Coders with Fastai and PyTorch: AI Applications Without a PhD. en. 1st ed. O’Reilly Media, Aug. 2020. ↩ ↩²
↩ ↩²
↩ ↩² ↩³ ↩⁴
$\textrm{[MP69]}$ M. Minsky and S. Papert. Perceptrons. MIT Press, 1969. ↩
$\textrm{[GBB11]}$: X. Glorot, A. Bordes, and Y. Bengio. “Deep Sparse Rectifer Neural Networks”. In: AISTATS. 2011. ↩ ↩²
$\textrm{[KSH12]}$: ↩ ↩²
$\textrm{[MHN13]}$: A. L. Maas, A. Y. Hannun, and A. Y. Ng. “Rectifier Nonlinearities Improve Neural Network Acoustic Models”. In: ICML. Vol. 28. 2013. ↩ ↩²
$\textrm{[CUH16]}$: D.-A. Clevert, T. Unterthiner, and S. Hochreiter. “Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)”. In: ICLR. 2016. ↩ ↩²
$\textrm{[RZL17]}$: P. Ramachandran, B. Zoph, and Q. V. Le. “Searching for Activation Functions”. In: (Oct. 2017). arXiv: 1710.05941 [cs.NE]. ↩ ↩²
$\textrm{[Kla+17]}$: G. Klambauer, T. Unterthiner, A. Mayr, and S.Hochreiter. “Self-Normalizing Neural Networks”. In: NIPS. 2017. ↩
$\textrm{[Maa+11]}$: A. L. Maas, R. E. Daly, P. T. Pham, D. Huang, A. Y. Ng, and C. Potts. “Learning Word Vectors for Sentiment Analysis”. In: Proc. ACL. 2011, pp. 142–150. ↩
$\textrm{[HAB19]}$ ↩
$\textrm{[HSW89]}$: ↩
$\textrm{[cyb89]}$: ↩
$\textrm{[Hor91]}$: ↩
$\textrm{[Has87]}$: ↩
$\textrm{[Mon+14]}$: ↩
$\textrm{[Rag+17]}$: ↩
$\textrm{[Pog+17]}$: ↩
$\textrm{[DHK13]}$: ↩
This popular analogy is due to Andrew Ng, who mentioned it in a keynote talk at the GPU Technology Conference (GTC) in 2015. His slides are available at https://bit.ly/38RTxzH. ↩
$\textrm{[Sej18]}$: ↩
$\textrm{[Ros58]}$: ↩
$\textrm{[Fuk80]}$: ↩
↩ ↩²
$\textrm{[GBC16]}$: ↩
$\textrm{[Kan+12]}$: ↩ ↩²
$\textrm{[MP43]}$: ↩
$\textrm{[Ben+15b]}$: ↩
$\textrm{[BS16]}$: ↩
$\textrm{[KH19]}$: ↩
$\textrm{[Doy+07]}$: ↩
$\textrm{[Sha88]}$: ↩
$\textrm{[Mar06]}$: ↩
$\textrm{[Yon19]}$: ↩
$\textrm{[KST82]}$: ↩
$\textrm{[GTA00]}$: ↩
$\textrm{[Gri20]}$: ↩
$\textrm{[MWK16]}$: ↩
$\textrm{[Has+17]}$: ↩
$\textrm{[Lak+17]}$ ↩
↩
↩
https://en.wikipedia.org/wiki/Backpropagation#History ↩
↩ ↩²
↩
↩
↩ ↩²
↩
↩ ↩² ↩³
↩
当应用于卷积层时，我们平均跨空间位置和跨示例，但不跨通道（因此 $\pmb{\mu}$ 的长度是通道数）。当应用于一个完全连接的层时，我们只需对示例进行平均（因此 $\pmb{\mu}$ 的长度就是层的宽度）。 ↩
↩
↩
↩
↩
↩
↩
↩ ↩²
↩ ↩²
↩
↩
↩
↩
↩
↩
↩
Geoff Hinton, who invented dropout, said he was inspired by a talk on sexual reproduction, which encourages genes to be individually useful (or at most depend on a small number of other genes), even when combined with random other genes. ↩
↩
↩
↩
↩
↩
Jittering is a common visualization trick in statistics, wherein points in a plot/display that would otherwise land on top of each other are dispersed with uniform additive noise ↩